Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C

Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation Tor Aamodt and Paul Chow University of Toronto 1

Presentation Outline îBackground / Motivation îFloating-to-Fixed-Point Conversion îArchitectural Support îExperimental Results îSummary / Future Directions Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 2 / 38

Background: University of Toronto DSP Project î Motivation: DSP Compiler/Architecture Co-design î First Generation Silicon (Sean Peng’s M. A. Sc. Thesis) tapedout Sept. 30, 1999: 108 pin PGA / 0. 35 µm CMOS / 63 MHz î 16 -bit Fixed-Point VLIW with Two-Level Instruction Fetching î Harvard Memory Architecture î 5 stage pipeline: IF 1 IF 2 ID EX WB î 7 function units: å å 2 integer units: 2 address units: 2 memory units: 1 control unit Tor Aamodt & Paul Chow University of Toronto 16. 0 multiply & 1. 15 multiply operations modulo addressing each tied to one data memory bank Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 3 / 38

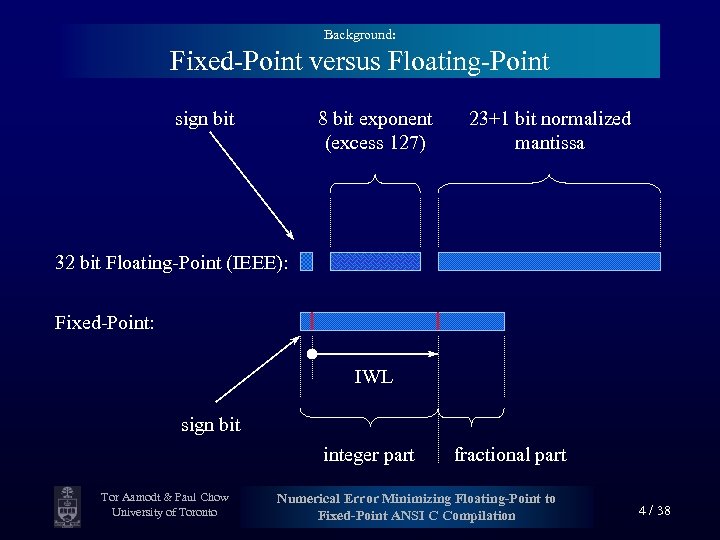Background: Fixed-Point versus Floating-Point sign bit 8 bit exponent (excess 127) 23+1 bit normalized mantissa 32 bit Floating-Point (IEEE): Fixed-Point: IWL sign bit integer part Tor Aamodt & Paul Chow University of Toronto fractional part Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 4 / 38

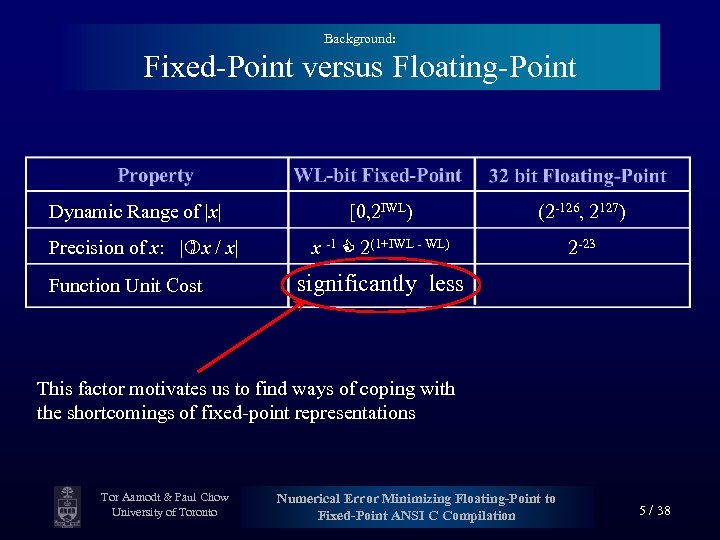Background: Fixed-Point versus Floating-Point Dynamic Range of |x| Precision of x: | x / x| Function Unit Cost [0, 2 IWL) (2 -126, 2127) x -1 2(1+IWL - WL) 2 -23 significantly less This factor motivates us to find ways of coping with the shortcomings of fixed-point representations Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 5 / 38

Motivation îWhy convert floating-point code to fixed-point code? Saves area and power. îWhy automate the process? Manual conversion is time-consuming and error-prone. îWhat qualities are we looking for in an automated conversion system? Good signal quality*. Fast code. Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 6 / 38

Background: Fixed-point Numerical Representations in Signal Processing îConsider a program P with associated inputs x(k) SP. Example: P an IIR filter, SP the set of all human speech samples x(k). îSignal Scaling: Integer Word Length (IWL) å definition: + an infinitesimally small number. Why? e. g. log 22 = Input, program variable, intermediate result, , and all inputs x For all definitions of output 1 Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 7 / 38

Background: Fixed-Point Arithmetic Operations Addition / Subtraction Overflow Guard Bits >> 1 B: A: >>( n + 1) (binary point alignment) n IWLA Multiplication A: IWLB B: IWLA+ IWLB ? ? ? A*B: Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 8 / 38

Presentation Outline îBackground Material / Motivation îFloating-to-Fixed-Point Conversion îArchitecture Support îExperimental Results îSummary / Future Directions Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 9 / 38

Conversion Process: Previous Work î‘Worst-Case Evaluation’: Markus Willems et. al. FRIDGE: An Interactive Code Generation Environment for HW/SW Co. Design. ICASSP, April 1997. îA ‘Statistical’ Approach: Ki-Il Kum, Jiyang Kang, and Wonyong Sung. A Floating-Point to Fixed-Point C Converter for Fixed-Point Digital Signal Processors. In Proc. 2 nd SUIF Compiler Workshop, August 1997. Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 10 / 38

Conversion Process: Overview “sin(x)” “utdsp_sin(x)” float *p, x, y, A[N], B[N]; fubar( float *p ) { for(floati=0; i < N; i++ ){ int sum = 0. 0; for( int i=0; i < N; B; p = (condition) ? A : i++) y +=sum += p[i]; x*p[i]; } Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 11 / 38

Conversion Process: Collecting Dynamic Range Information Consider the ANSI C code: float a, b, x[N]; y = a*x[i] + b*x[i+1]; Equivalent Expression Tree: ID Assignment: “ 1” : tmp_1 a * x[i] “ 0” : y + b Code Instrumentation: tmp_1 = a*x[i]; profile(tmp_1, 1); tmp_2 = b*x[i+1]; profile(tmp_2, 2); y = tmp_1 * tmp_2; profile(y, 0); * “ 2” : tmp_2 Tor Aamodt & Paul Chow University of Toronto x[i+1] fin Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 12 / 38

Conversion Process: Desired Result Continuation of Previous Example : float a, b, x[N]; y = a*x[i] + b*x[i+1]; int a, b, x[N]; y = a • x[i] >> 2 + b • x[i+1]; 1. Type Conversion 2. Scaling Operations 3. Fractional Fixed-Point Operations Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 13 / 38

Conversion Process: Type Conversion / Scaling Operation Generation îType conversion: {float, double} int îScaling Operations are added to expression trees using a post-order traversal. . . îTwo previous algorithms from the literature for generating scaling operations. . . îNeither use Intermediate Result Profile data, instead, they combine range information from leaf nodes in a bottom-up fashion. îIs Useful Information Lost? Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 14 / 38

Conversion Process: IRP: Using Intermediate Result Profile Data î‘Worst-Case Evaluation’: Markus Willems et. al. FRIDGE: An Interactive Code Generation Environment for HW/SW Co. Design. ICASSP, April 1997. îA ‘Statistical’ Approach: Ki-Il Kum, Jiyang Kang, and Wonyong Sung. A Floating-Point to Fixed-Point C Converter for Fixed-Point Digital Signal Processors. In Proc. 2 nd SUIF Compiler Workshop, August 1997. îUTDSP Algorithms: IRP, IRP-SA å Each node has a measured IWL and a current IWL å Measured: IWL as determined by profiling å Current: IWL due to scaling operations within Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 15 / 38

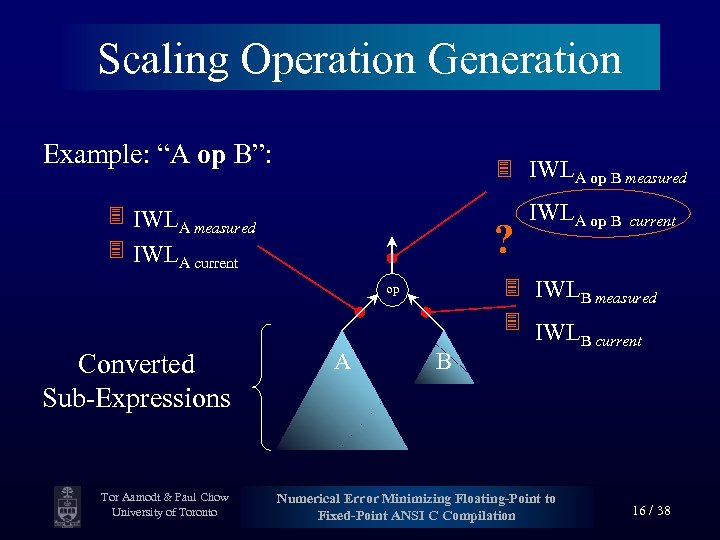Scaling Operation Generation Example: “A op B”: IWLA op B measured IWLA current ? op Converted Sub-Expressions Tor Aamodt & Paul Chow University of Toronto A B IWLA op B current IWLB measured IWL B current Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 16 / 38

IRP: Additive Operations For example, assume |A| > |B|, and IWLA+B measured IWLA measured “A ± B” A: B: >> n n “A B” where: IWLA+B current Tor Aamodt & Paul Chow University of Toronto “(A << n. A) (B >> [n-n. B])” n. A = IWLA n. B = IWLA n = IWLA current measured - IWLA IWLB measured Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 17 / 38

IRP: Multiplication “A • B” where: “(A << n. A) • (B << n. B)” n. A = IWLA n. B = IWLA • B current = Tor Aamodt & Paul Chow University of Toronto current measured n. A + n B - + IWLB IWLA IWLB measured Note: Typo in Notes! Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 18 / 38

IRP-SA: Using ‘Shift Absorption’ Problem: y = (a*x[i] + b*x[i+1]>>1) << 1 Question: Answer: Is information discarded unnecessarily here? Yes! Consider the following alternative: y = (a*x[i]<<1) + b*x[i+1] Assuming 2’s-complement arithmetic, this expression results in a more precise answer. Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 20 / 38

Presentation Outline îBackground Material / Motivation îFloating-to-Fixed-Point Conversion îArchitecture Support îExperimental Results îSummary / Future Directions Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 21 / 38

Architectural Support Common occurrence (using IRP-SA): A • B << n Fractional Multiplication with integrated Left Shift: A: Left Shift B: A*B: Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 22 / 38

Presentation Outline îBackground Material / Motivation îFloating-to-Fixed-Point Conversion îArchitecture Support îExperimental Results îSummary / Future Directions Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 23 / 38

Experimental Results îFour test-cases presented in paper: (1) (2) (3) (4) 4 th Order IIR Filter 1024 Point Radix 2 Decimation in Time FFT Nonlinear Feedback Control System 16 th Order Lattice Filter î Look at (1) in detail, summarize results for others. î Explore some interesting properties exhibited in (4) that are indicative of possible future improvements. Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 24 / 38

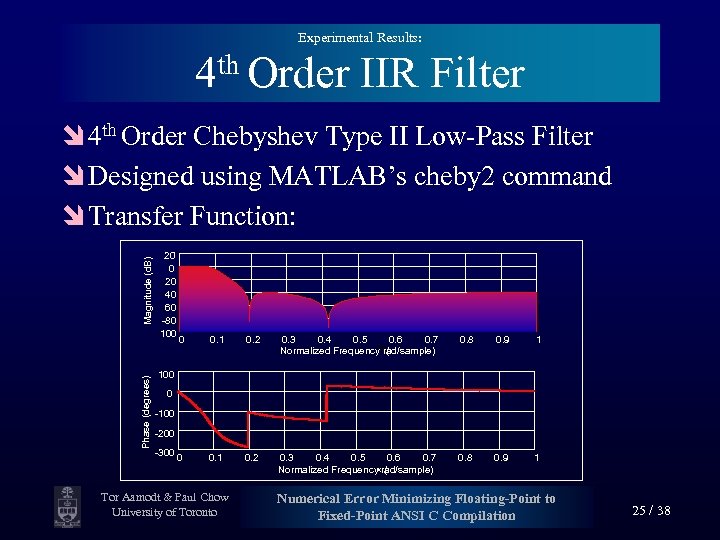Experimental Results: 4 th Order IIR Filter Phase (degrees) Magnitude (d. B) î 4 th Order Chebyshev Type II Low-Pass Filter î Designed using MATLAB’s cheby 2 command î Transfer Function: 20 0 -20 -40 -60 -80 -100 0 0. 1 0. 2 0. 3 0. 4 0. 5 0. 6 0. 7 ´p( Normalized Frequency rad/sample) 0. 8 0. 9 1 0 0. 1 0. 2 0. 3 0. 4 0. 5 0. 6 0. 7 Normalized Frequency rad/sample) ( ´p 0. 8 0. 9 1 100 0 -100 -200 -300 Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 25 / 38

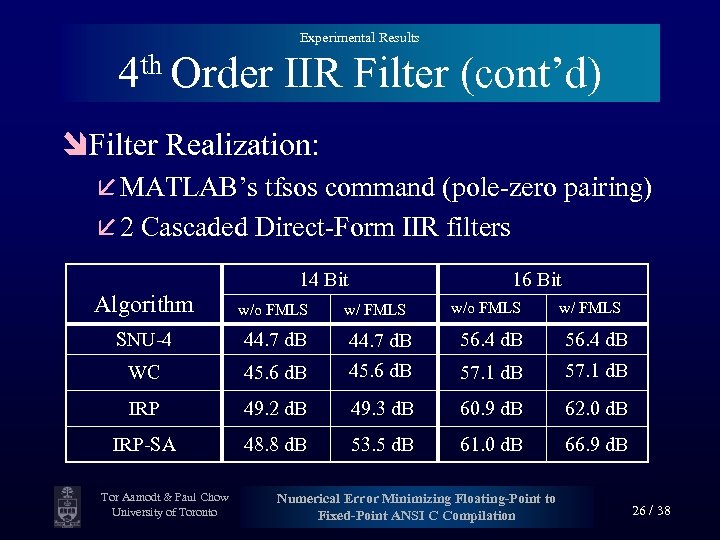Experimental Results 4 th Order IIR Filter (cont’d) îFilter Realization: å MATLAB’s tfsos command (pole-zero pairing) å 2 Cascaded Direct-Form IIR filters 14 Bit Algorithm w/o FMLS SNU-4 44. 7 d. B WC 16 Bit w/ FMLS w/o FMLS w/ FMLS 56. 4 d. B 45. 6 d. B 44. 7 d. B 45. 6 d. B 57. 1 d. B IRP 49. 2 d. B 49. 3 d. B 60. 9 d. B 62. 0 d. B IRP-SA 48. 8 d. B 53. 5 d. B 61. 0 d. B 66. 9 d. B Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 26 / 38

Experimental Results 4 th Order IIR Filter (cont’d) IRP: (A 2[0]*t 2 - A 2[1]*D 2[0] << 1) + (A 2[2]*D 2[1] << 1 ) << 2 IRP-SA: (A 2[0]*t 2 << 3) - (A 2[1]*D 2[0] << 3) + (A 2[2]*D 2[1] << 3) Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 27 / 38

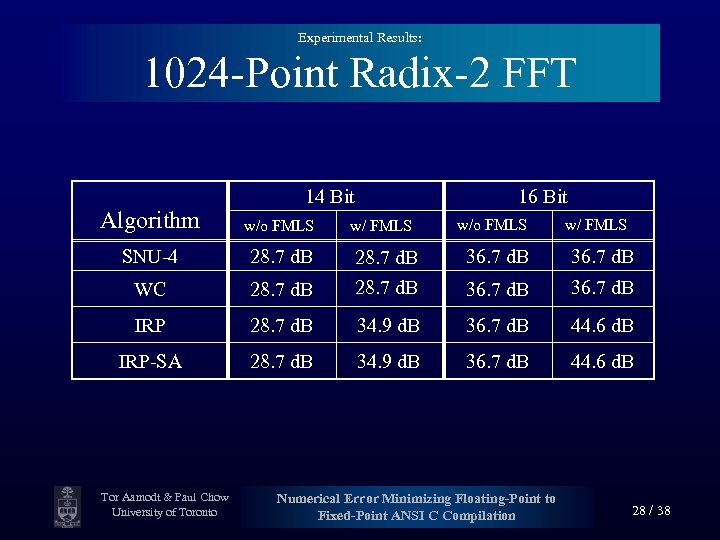Experimental Results: 1024 -Point Radix-2 FFT 14 Bit Algorithm w/o FMLS SNU-4 28. 7 d. B WC 16 Bit w/ FMLS w/o FMLS w/ FMLS 36. 7 d. B 28. 7 d. B 36. 7 d. B IRP 28. 7 d. B 34. 9 d. B 36. 7 d. B 44. 6 d. B IRP-SA 28. 7 d. B 34. 9 d. B 36. 7 d. B 44. 6 d. B Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 28 / 38

Experimental Results: Rotational Inverted Pendulum U of T System Control Group Non-linear Testbench Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 29 / 38

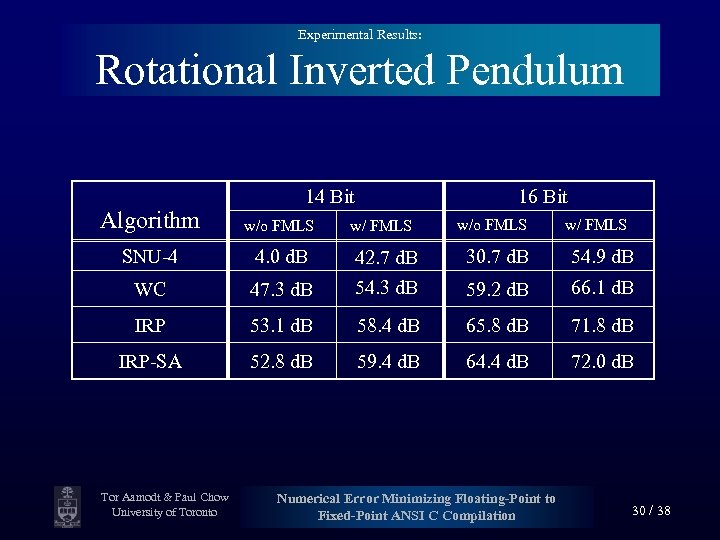Experimental Results: Rotational Inverted Pendulum 14 Bit Algorithm w/o FMLS SNU-4 4. 0 d. B WC 16 Bit w/ FMLS w/o FMLS w/ FMLS 30. 7 d. B 54. 9 d. B 47. 3 d. B 42. 7 d. B 54. 3 d. B 59. 2 d. B 66. 1 d. B IRP 53. 1 d. B 58. 4 d. B 65. 8 d. B 71. 8 d. B IRP-SA 52. 8 d. B 59. 4 d. B 64. 4 d. B 72. 0 d. B Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 30 / 38

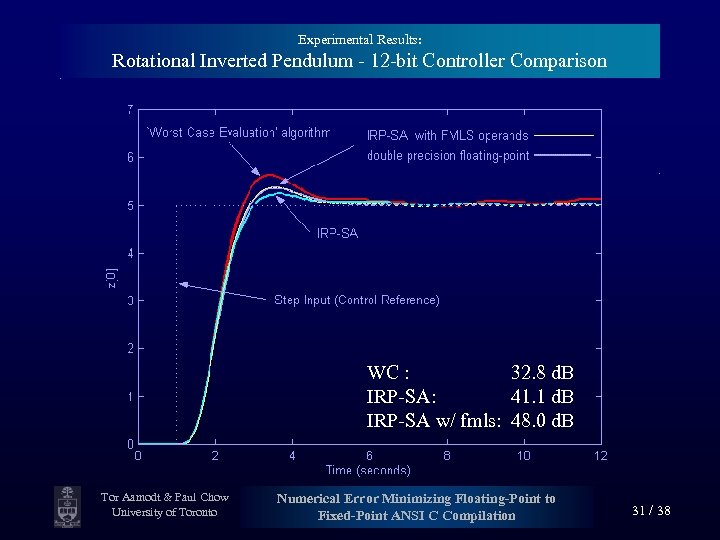Experimental Results: Rotational Inverted Pendulum - 12 -bit Controller Comparison WC : 32. 8 d. B IRP-SA: 41. 1 d. B IRP-SA w/ fmls: 48. 0 d. B Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 31 / 38

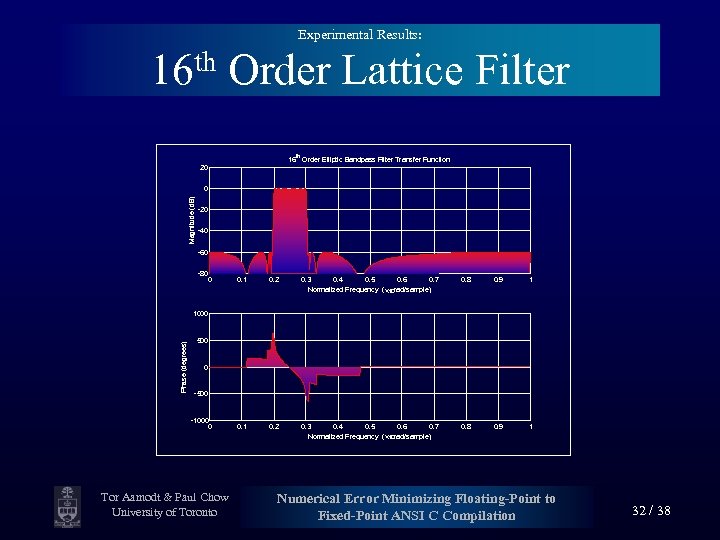Experimental Results: th 16 Order Lattice Filter 16 th Order Elliptic Bandpass Filter Transfer Function 20 Magnitude (d. B) 0 -20 -40 -60 -80 0 0. 1 0. 2 0. 3 0. 4 0. 5 0. 6 0. 7 Normalized Frequency (´p rad/sample) 0. 8 0. 9 1 Phase (degrees) 1000 500 0 -500 -1000 0 Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 32 / 38

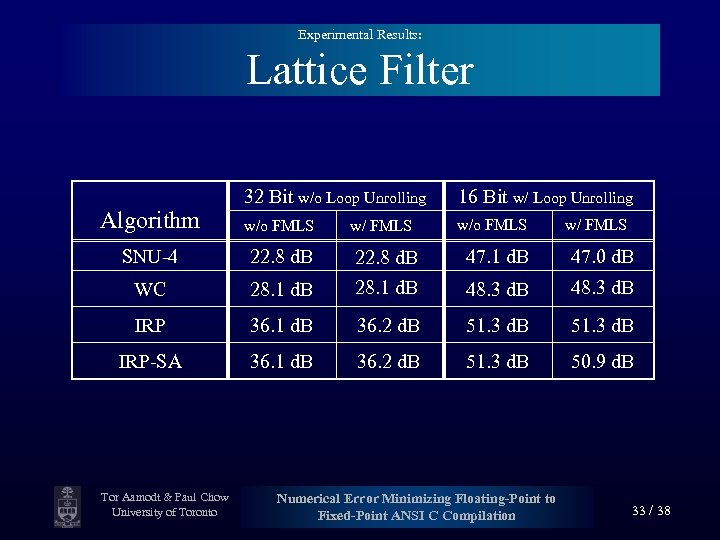Experimental Results: Lattice Filter Algorithm 32 Bit w/o Loop Unrolling 16 Bit w/ Loop Unrolling w/o FMLS SNU-4 22. 8 d. B WC w/ FMLS 47. 1 d. B 47. 0 d. B 28. 1 d. B 22. 8 d. B 28. 1 d. B 48. 3 d. B IRP 36. 1 d. B 36. 2 d. B 51. 3 d. B IRP-SA 36. 1 d. B 36. 2 d. B 51. 3 d. B 50. 9 d. B Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 33 / 38

Experimental Results: Lattice Filter #define N 16; double state[N+1], K[N], V[N+1]; double lattice( double x ) { double y = 0. 0; for( int i=0; i < N; i++ ) { x = x - K[N-i-1] * state[N-i-1]; state[N-i] = state[N-i-1] + K[N-i-1]*x; y = y + V[N-i]*state[N-i]; } state[0] = x; return y + V[0]*state[0]; } Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 34 / 38

Experimental Results: Lattice Filter îObservation: Wide Dynamic Ranges of “state”, “V”, “x”, and “y” are due to ‘Name Dependencies’ of array elements and accumulators when assigning integer word lengths. î Can use Loop Unrolling + Renaming to break dependencies and achieve far better results (iteration dependant analysis mentioned in FRIDGE paper—however no experimental results reported) Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 35 / 38

Presentation Outline îBackground Material / Motivation îFloating-to-Fixed-Point Conversion îArchitecture Support îExperimental Results îSummary / Future Directions Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 36 / 38

Summary îIntermediate result profile data can used to reduce numerical error of fixed-point code. îA fractional multiply with integrated left shift operation can improve the results, especially when combined with the IRP-SA algorithm. îImprovements between 3. 0 d. B and 12. 8 d. B have been observed so far. Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 37 / 38

Future Directions îStructural Transformations îExtended Precision Arithmetic îOverflows due to accumulated rounding error — use two profiling phases to estimate the effect of ‘second-order’ interactions. Tor Aamodt & Paul Chow University of Toronto Numerical Error Minimizing Floating-Point to Fixed-Point ANSI C Compilation 38 / 38