Numerical Algorithms x x-1 0 1 1 2

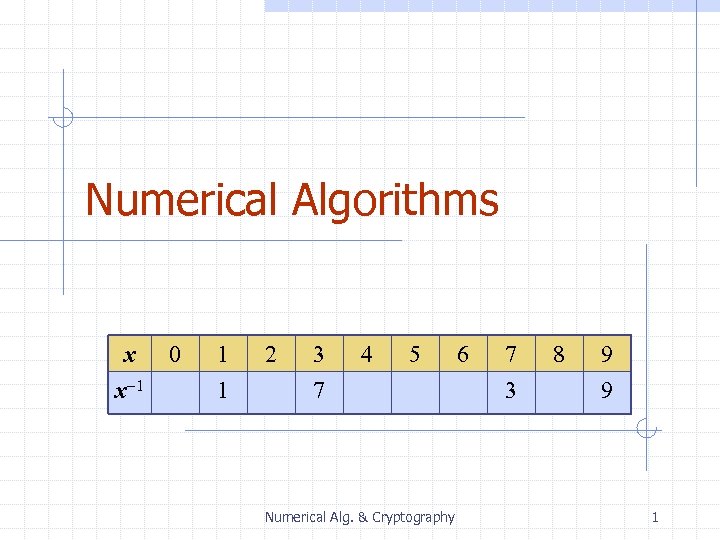Numerical Algorithms x x-1 0 1 1 2 3 7 4 5 Numerical Alg. & Cryptography 6 7 3 8 9 9 1

Outline Divisibility and primes Modular arithmetic Euclid’s GCD algorithm Multiplicative inverses Powers Fermat’s little theorem Euler’s theorem Numerical Alg. & Cryptography 2

Facts About Numbers Prime number p: n n n p is an integer p 2 The only divisors of p are 1 and p Examples n n 2, 7, 19 are primes -3, 1, 6 are not primes Prime decomposition of a positive integer n: n = p 1 e 1 … pkek Example: n 200 = 23 52 Fundamental Theorem of Arithmetic The prime decomposition of a positive integer is unique Numerical Alg. & Cryptography 3

Greatest Common Divisor The greatest common divisor (GCD) of two positive integers a and b, denoted gcd(a, b), is the largest positive integer that divides both a and b The above definition is extended to arbitrary integers Examples: gcd(18, 30) = 6 gcd(-21, 49) = 7 gcd(0, 20) = 20 Two integers a and b are said to be relatively prime if gcd(a, b) = 1 Example: n Integers 15 and 28 are relatively prime Numerical Alg. & Cryptography 4

Modular Arithmetic Modulo operator for a positive integer n r = a mod n equivalent to a = r + kn and r = a - a/n n Example: 29 mod 13 = 3 29 = 3 + 2 13 13 mod 13 = 0 + 1 13 -1 mod 13 = 12 12 = -1 + 1 13 Modulo and GCD: gcd(a, b) = gcd(b, a mod b) Example: gcd(21, 12) = 3 gcd(12, 21 mod 12) = gcd(6, 9) = 3 Numerical Alg. & Cryptography 5

Euclid’s GCD Algorithm Euclid’s algorithm for computing the GCD repeatedly applies the formula gcd(a, b) = gcd(b, a mod b) Example n gcd(412, 260) = 4 Algorithm Euclid. GCD(a, b) Input integers a and b Output gcd(a, b) if b = 0 return a else return Euclid. GCD(b, a mod b) a 412 260 152 108 44 20 4 b 260 152 108 44 20 4 0 Numerical Alg. & Cryptography 6

Analysis Let ai and bi be the arguments of the i-th recursive call of algorithm Euclid. GCD We have ai + 2 = bi + 1 = ai mod ai + 1 < ai + 1 Sequence a 1, a 2, …, an decreases exponentially, namely ai + 2 ½ ai for i > 1 Case 1 ai + 1 ½ ai Case 2 ai + 1 > ½ ai ai + 2 < ai + 1 ½ ai ai + 2 = ai mod ai + 1 = ai - ai + 1 ½ ai Thus, the maximum number of recursive calls of algorithm Euclid. GCD(a. b) is 1 + 2 log max(a. b) Algorithm Euclid. GCD(a, b) executes O(log max(a, b)) arithmetic operations Numerical Alg. & Cryptography 7

Multiplicative Inverses (1) The residues modulo a positive integer n are the set Zn = {0, 1, 2, …, (n - 1)} Let x and y be two elements of Zn such that xy mod n = 1 We say that y is the multiplicative inverse of x in Zn and we write y = x-1 Example: n x x-1 Multiplicative inverses of the residues modulo 11 0 1 1 2 6 3 4 4 3 5 9 6 2 Numerical Alg. & Cryptography 7 8 8 7 9 5 10 10 8

Multiplicative Inverses (2) Theorem An element x of Zn has a multiplicative inverse if and only if x and n are relatively prime Example n The elements of Z 10 with a multiplicative inverse are 1, 3, 5, 7 Corollary If is prime, every nonzero residue in Zp has a multiplicative inverse Theorem A variation of Euclid’s GCD algorithm computes the multiplicative inverse of an element x of Zn or determines that it does not exist x x-1 0 1 1 2 3 7 4 5 6 Numerical Alg. & Cryptography 7 3 8 9 9 9

Powers Let p be a prime The sequences of successive powers of the elements of Zp exhibit repeating subsequences The sizes of the repeating subsequences and the number of their repetitions are the divisors of p - 1 Example (p = 7) x x 2 x 3 x 4 x 5 x 6 1 1 1 2 4 1 3 2 6 4 5 1 4 2 1 5 4 6 2 3 1 6 1 6 1 Numerical Alg. & Cryptography 10

Fermat’s Little Theorem Let p be a prime. For each nonzero residue x of Zp, we have xp - 1 mod p = 1 Example (p = 5): 14 mod 5 = 1 34 mod 1 = 81 mod 5 = 1 24 mod 1 = 16 mod 5 = 1 44 mod 1 = 256 mod 5 = 1 Corollary Let p be a prime. For each nonzero residue x of Zp, the multiplicative inverse of x is xp - 2 mod p Proof x(xp - 2 mod p) mod p = xxp - 2 mod p = xp - 1 mod p = 1 Numerical Alg. & Cryptography 11

Euler’s Theorem The multiplicative group for Zn, denoted with Z*n, is the subset of elements of Zn relatively prime with n The totient function of n, denoted with f(n), is the size of Z*n Example Z*10 = { 1, 3, 7, 9 } f(10) = 4 If p is prime, we have Z*p = {1, 2, …, (p - 1)} f(p) = p - 1 Theorem For each element x of Z*n, we have xf(n) mod n = 1 Example (n = 10) 3 f(10) mod 10 = 34 mod 10 = 81 mod 10 = 1 7 f(10) mod 10 = 74 mod 10 = 2401 mod 10 = 1 9 f(10) mod 10 = 94 mod 10 = 6561 mod 10 = 1 Numerical Alg. & Cryptography 12

The Fast Fourier Transform Numerical Alg. & Cryptography 13

Outline and Reading Polynomial Multiplication Problem Primitive Roots of Unity (§ 10. 4. 1) The Discrete Fourier Transform (§ 10. 4. 2) The FFT Algorithm (§ 10. 4. 3) Integer Multiplication (§ 10. 4. 4) Java FFT Integer Multiplication (§ 10. 5) Numerical Alg. & Cryptography 14

Polynomials Polynomial: In general, Numerical Alg. & Cryptography 15

Polynomial Evaluation Horner’s Rule: n Given coefficients (a 0, a 1, a 2, …, an-1), defining polynomial n Given x, we can evaluate p(x) in O(n) time using the equation Eval(A, x): n n [Where A=(a 0, a 1, a 2, …, an-1)] If n=1, then return a 0 Else, w Let A’=(a 1, a 2, …, an-1) w return a 0+x*Eval(A’, x) [assume this can be done in constant time] Numerical Alg. & Cryptography 16

Polynomial Multiplication Problem Given coefficients (a 0, a 1, a 2, …, an-1) and (b 0, b 1, b 2, …, bn-1) defining two polynomials, p() and q(), and number x, compute p(x)q(x). Horner’s rule doesn’t help, since where A straightforward evaluation would take O(n 2) time. The “magical” FFT will do it in O(n log n) time. Numerical Alg. & Cryptography 17

Polynomial Interpolation & Polynomial Multiplication Given a set of n points in the plane with distinct x-coordinates, there is exactly one (n-1)-degree polynomial going through all these points. Alternate approach to computing p(x)q(x): n n n Calculate p() on 2 n x-values, x 0, x 1, …, x 2 n-1. Calculate q() on the same 2 n x values. Find the (2 n-1)-degree polynomial that goes through the points {(x 0, p(x 0)q(x 0)), (x 1, p(x 1)q(x 1)), …, (x 2 n-1, p(x 2 n-1)q(x 2 n-1))}. Unfortunately, a straightforward evaluation would still take O(n 2) time, as we would need to apply an O(n)-time Horner’s Rule evaluation to 2 n different points. The “magical” FFT will do it in O(n log n) time, by picking 2 n points that are easy to evaluate… Numerical Alg. & Cryptography 18

Primitive Roots of Unity A number w is a primitive n-th root of unity, for n>1, if n n wn = 1 The numbers 1, w, w 2, …, wn-1 are all distinct Example 1: n n Z*11: 2, 6, 7, 8 are 10 -th roots of unity in Z*11 22=4, 62=3, 72=5, 82=9 are 5 -th roots of unity in Z*11 2 -1=6, 3 -1=4, 4 -1=3, 5 -1=9, 6 -1=2, 7 -1=8, 8 -1=7, 9 -1=5 Example 2: The complex number e 2 pi/n is a primitive n-th root of unity, where Numerical Alg. & Cryptography 19

Properties of Primitive Roots of Unity Inverse Property: If w is a primitive root of unity, then w -1=wn-1 n Proof: wwn-1=wn=1 Cancellation Property: For non-zero -n

The Discrete Fourier Transform Given coefficients (a 0, a 1, a 2, …, an-1) for an (n-1)-degree polynomial p(x) The Discrete Fourier Transform is to evaluate p at the values n 1, w, w 2, …, wn-1 We produce (y 0, y 1, y 2, …, yn-1), where yj=p(wj) That is, n Matrix form: y=Fa, where F[i, j]=wij. n n The Inverse Discrete Fourier Transform recovers the coefficients of an (n-1)-degree polynomial given its values at 1, w, w 2, …, wn-1 n Matrix form: a=F -1 y, where F -1[i, j]=w-ij/n. Numerical Alg. & Cryptography 21

Correctness of the inverse DFT The DFT and inverse DFT really are inverse operations Proof: Let A=F -1 F. We want to show that A=I, where If i=j, then If i and j are different, then Numerical Alg. & Cryptography 22

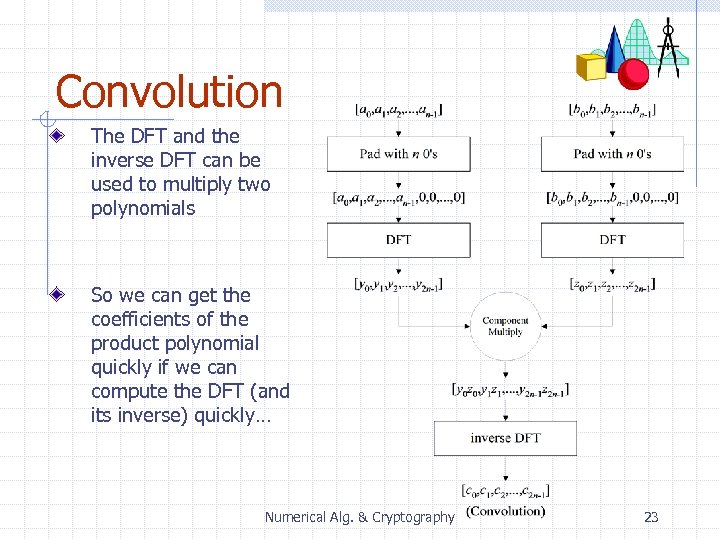Convolution The DFT and the inverse DFT can be used to multiply two polynomials So we can get the coefficients of the product polynomial quickly if we can compute the DFT (and its inverse) quickly… Numerical Alg. & Cryptography 23

The Fast Fourier Transform The FFT is an efficient algorithm for computing the DFT The FFT is based on the divide-and-conquer paradigm: n If n is even, we can divide a polynomial into two polynomials and we can write Numerical Alg. & Cryptography 24

The FFT Algorithm The running time is O(n log n). [inverse FFT is similar] Numerical Alg. & Cryptography 25

Multiplying Big Integers Given N-bit integers I and J, compute IJ. Assume: we can multiply words of O(log N) bits in constant time. Setup: Find a prime p=cn+1 that can be represented in one word, and set m=(log p)/3, so that we can view I and J as n-length vectors of m-bit words. Finding a primitive root of unity. n n Find a generator x of Z*p. Then w=xc is a primitive n-th root of unity in Z*p (arithmetic is mod p) Apply convolution and FFT algorithm to compute the convolution C of the vector representations of I and J. Then compute K is a vector representing IJ, and takes O(n log n) time to compute. Numerical Alg. & Cryptography 26

Java Example: Multiplying Big Integers Setup: Define Big. Int class, and include essential parameters, including the prime, P, and primitive root of unity, OMEGA. 10; Numerical Alg. & Cryptography 27

Java Integer Multiply Method Use convolution to multiply two big integers, this and val: Numerical Alg. & Cryptography 28

Java FFT in Z*p Numerical Alg. & Cryptography 29

Support Methods for Java FFT in Z*p Numerical Alg. & Cryptography 30

Non-recursive FFT There is also a non-recursive version of the FFT n n n Performs the FFT in place Precomputes all roots of unity Performs a cumulative collection of shuffles on A and on B prior to the FFT, which amounts to assigning the value at index i to the index bit-reverse(i). The code is a bit more complex, but the running time is faster by a constant, due to improved overhead Numerical Alg. & Cryptography 31

Experimental Results Log-log scale shows traditional multiply runs in O(n 2) time, while FFT versions are almost linear Numerical Alg. & Cryptography 32

Cryptography plaintext encrypt Numerical Alg. & Cryptography ciphertext 33

Outline Traditional cryptography Statistical attacks Secret-key encryption Public-key encryption Numerical Alg. & Cryptography 34

Encryption Scenario: n n Alice wants to send a message (plaintext p) to Bob. The communication channel is insecure and can be eavesdropped If Alice and Bob have previously agreed on an encryption scheme (cipher), the message can be sent encrypted (ciphertext c) Issues: n n What is a good encryption scheme? What is the complexity of encrypting/decrypting? What is the size of the ciphertext, relative to the plaintext? If Alice and Bob have never interacted before, how can they agree on an encryption scheme? plaintext encrypt ciphertext Numerical Alg. & Cryptography decrypt plaintext 35

Traditional Cryptography Ciphers were already studied in ancient times Caesar’s cipher: n n replace a with d replace b with e. . . replace z with c Caesar’s cipher is an example of a monoalphabetic substitution cipher, which permutes the characters Armed with simple statistical knowledge, one can easily break a monoalphabetic substitution cipher n n n most frequent letters in English: e, t, o, a, n, i, . . . most frequent digrams: th, in, er, re, an, . . . most frequent trigrams: the, ing, and, ion, . . . The first description of the frequency analysis attack appears in a book written in the 9 th century by the Arab philosopher al-Kindi Numerical Alg. & Cryptography 36

Statistical Attacks Armed with statistical knowledge about the plaintext language, one can easily break a monoalphabetic substitution cipher n n n Most frequent characters in English: e, t, o, a, n, i, . . . Most frequent digrams: th, in, er, re, an, . . . Most frequent trigrams: the, ing, and, ion, . . . The first description of the frequency analysis attack appears in a book written in the 9 th century by the Arab philosopher al-Kindi Example (S. Singh, The Code Book, 1999): PCQ VMJYPD LBYK LYSO KBXBJXWXV BXV ZCJPO EYPD KBXBJYUXJ LBJOO KCPK. CP LBO LBCMKXPV IYJKL PYDBL, QBOP KBO BXV OPVOV LBO LXRO CI SX'XJMI, KBO JCKO XPV EYKKOV LBO DJCMPV ZOICJO BYS, KXUYPD: “DJOXL EYPD, ICJ X LBCMKXPV CPO PYDBLK Y BXNO ZOOP JOACMPLYPD LC UCM LBO IXZROK CI FXKL XDOK XPV LBO RODOPVK CI XPAYOPL EYPDK. SXU Y SXEO KC ZCRV XK LC AJXNO X IXNCMJ CI UCMJ SXGOKLU? ” OFYRCDMO, LXROK IJCS LBO LBCMKXPV CPO PYDBLK Numerical Alg. & Cryptography 37

Frequency Analysis (1) We identify the most common characters, digrams and trigrams in the ciphertext Example PCQ VMJYPD LBYK LYSO KBXBJXWXV BXV ZCJPO EYPD KBXBJYUXJ LBJOO KCPK. CP LBO LBCMKXPV IYJKL PYDBL, QBOP KBO BXV OPVOV LBO LXRO CI SX'XJMI, KBO JCKO XPV EYKKOV LBO DJCMPV ZOICJO BYS, KXUYPD: “DJOXL EYPD, ICJ X LBCMKXPV CPO PYDBLK Y BXNO ZOOP JOACMPLYPD LC UCM LBO IXZROK CI FXKL XDOK XPV LBO RODOPVK CI XPAYOPL EYPDK. SXU Y SXEO KC ZCRV XK LC AJXNO X IXNCMJ CI UCMJ SXGOKLU? ” OFYRCDMO, LXROK IJCS LBO LBCMKXPV CPO PYDBLK First guess: n LBO is THE Numerical Alg. & Cryptography 38

Frequency Analysis (2) Assuming LBO represents THE, we replace L with T, B with H, and O with E and get PCQ VMJYPD THYK TYSE KHXHJXWXV HXV ZCJPE EYPD KHXHJYUXJ THJEE KCPK. CP THE THCMKXPV IYJKT PYDHT, QHEP KHO HXV EPVEV THE LXRE CI SX'XJMI, KHE JCKE XPV EYKKEV THE DJCMPV ZEICJE HYS, KXUYPD: “DJEXT EYPD, ICJ X THCMKXPV CPE PYDHTK Y HXNE ZEEP JEACMPTYPD TC UCM THE IXZREK CI FXKT XDEK XPV THE REDEPVK CI XPAYEPT EYPDK. SXU Y SXEE KC ZCRV XK TC AJXNE X IXNCMJ CI UCMJ SXGEKTU? ” EFYRCDME, TXREK IJCS THE THCMKXPV CPE PYDBTK Numerical Alg. & Cryptography 39

Decryption Code: X Z A V O I D B Y G E R S P C F H J K L M N Q T U W A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Ciphertext: PCQ VMJYPD LBYK LYSO KBXBJXWXV BXV ZCJPO EYPD KBXBJYUXJ LBJOO KCPK. CP LBO LBCMKXPV IYJKL PYDBL, QBOP KBO BXV OPVOV LBO LXRO CI SX'XJMI, KBO JCKO XPV EYKKOV LBO DJCMPV ZOICJO BYS, KXUYPD: “DJOXL EYPD, ICJ X LBCMKXPV CPO PYDBLK Y BXNO ZOOP JOACMPLYPD LC UCM LBO IXZROK CI FXKL XDOK XPV LBO RODOPVK CI XPAYOPL EYPDK. SXU Y SXEO KC ZCRV XK LC AJXNO X IXNCMJ CI UCMJ SXGOKLU? ” OFYRCDMO, LXROK IJCS LBO LBCMKXPV CPO PYDBLK Plaintext: Now during this time Shahrazad had borne King Shahriyar three sons. On the thousand first night, when she had ended the tale of Ma'aruf, she rose and kissed the ground before him, saying: “Great King, for a thousand one nights I have been recounting to you the fables of past ages and the legends of ancient kings. May I make so bold as to crave a favour of your majesty? ” Epilogue, Tales from the Thousand One Nights Numerical Alg. & Cryptography 40

Secret-Key Encryption A secret-key cipher uses a unique key K to encrypt and decrypt Caesar’s generalized cipher uses the modular addition of each character (viewed as an integer) with the key: C[i] = P[i] + K mod m P[i] = C[i] - K mod m More secure secret-key encryption schemes have been devised in this century Examples: n n DES 3 DES IDEA BLOWFISH With private-key encryption, a distinct secret key must be established for every pair of parties Numerical Alg. & Cryptography 41

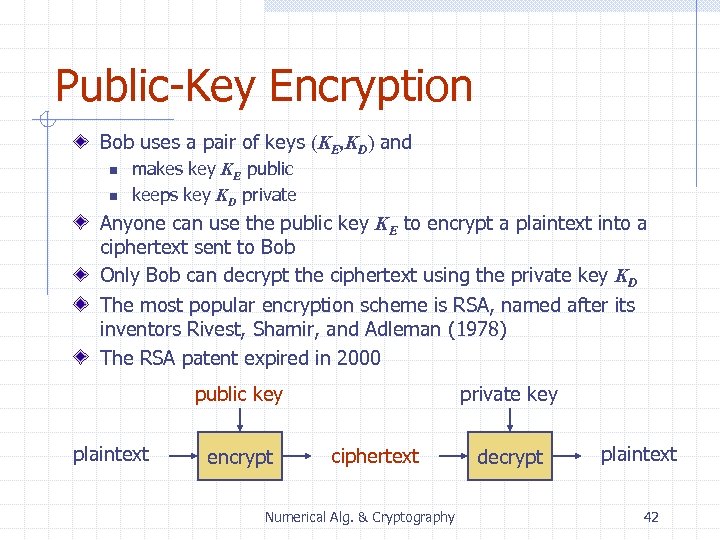Public-Key Encryption Bob uses a pair of keys (KE, KD) and n n makes key KE public keeps key KD private Anyone can use the public key KE to encrypt a plaintext into a ciphertext sent to Bob Only Bob can decrypt the ciphertext using the private key KD The most popular encryption scheme is RSA, named after its inventors Rivest, Shamir, and Adleman (1978) The RSA patent expired in 2000 public key plaintext encrypt private key ciphertext Numerical Alg. & Cryptography decrypt plaintext 42

RSA Cryptosystem Bits PCs Memory 430 1 128 MB 760 215, 000 4 GB 1, 020 342 106 170 GB 1, 620 1. 6 1015 120 TB Numerical Alg. & Cryptography 43

Outline Euler’s theorem (§ 10. 1. 3) RSA cryptosystem (§ 10. 2. 3) n n Definition Example Security Correctness Algorithms for RSA n n n Modular power (§ 10. 1. 4) Modular inverse (§ 10. 1. 5) Randomized primality testing (§ 10. 1. 6) Numerical Alg. & Cryptography 44

Euler’s Theorem The multiplicative group for Zn, denoted with Z*n, is the subset of elements of Zn relatively prime with n The totient function of n, denoted with f(n), is the size of Z*n Example Z*10 = { 1, 3, 7, 9 } f(10) = 4 If p is prime, we have Z*p = {1, 2, …, (p - 1)} f(p) = p - 1 Euler’s Theorem For each element x of Z*n, we have xf(n) mod n = 1 Example (n = 10) 3 f(10) mod 10 = 34 mod 10 = 81 mod 10 = 1 7 f(10) mod 10 = 74 mod 10 = 2401 mod 10 = 1 9 f(10) mod 10 = 94 mod 10 = 6561 mod 10 = 1 Numerical Alg. & Cryptography 45

RSA Cryptosystem Setup: Example n = pq, with p and q primes n e relatively prime to f(n) = (p - 1) (q - 1) n d inverse of e in Zf(n) n n w p = 7, q = 17 w n = 7 17 = 119 w f(n) = 6 16 = 96 we = 5 w d = 77 Keys: Public key: KE = (n, e) n Private key: KD = d n Encryption: Plaintext M in Zn n C = Me mod n Setup: n Keys: w public key: (119, 5) w private key: 77 n Encryption: w M = 19 w C = 195 mod 119 = 66 n Decryption: n n Decryption: w C = 6677 mod 119 = 19 M = Cd mod n Numerical Alg. & Cryptography 46

Complete RSA Example Setup: Encryption p = 5, q = 11 n n = 5 11 = 55 n f(n) = 4 10 = 40 ne = 3 n d = 27 (3 27 = 81 = 2 40 + 1) n n C = M 3 mod 55 Decryption Numerical Alg. & Cryptography n M = C 27 mod 55 47

Security The security of the RSA cryptosystem is based on the widely believed difficulty of factoring large numbers n The best known factoring algorithm (general number field sieve) takes time exponential in the number of bits of the number to be factored The RSA challenge, sponsored by RSA Security, offers cash prizes for the factorization of given large numbers In April 2002, prizes ranged from $10, 000 (576 bits) to $200, 000 (2048 bits) In 1999, a 512 -bit number was factored in 4 months using the following computers: n 160 n n n 175 -400 MHz SGI and Sun 8 250 MHz SGI Origin 120 300 -450 MHz Pentium II 4 500 MHz Digital/Compaq Estimated resources needed to factor a number within one year Bits PCs Memory 430 1 128 MB 760 215, 000 4 GB 1, 020 342 106 170 GB 1, 620 1. 6 1015 120 TB Numerical Alg. & Cryptography 48

Correctness We show the correctness of the RSA cryptosystem for the case when the plaintext M does not divide n Namely, we show that (Me)d mod n = M Since ed mod f(n) = 1, there is an integer k such that ed = kf(n) + 1 Since M does not divide n, by Euler’s theorem we have Mf(n) mod n = 1 Thus, we obtain (Me)d mod n = Med mod n = Mkf(n) + 1 mod n = MMkf(n) mod n = M (Mf(n))k mod n = M (Mf(n) mod n)k mod n = M (1)k mod n = M See the book for the proof of correctness in the case when the plaintext M divides n Numerical Alg. & Cryptography 49

Algorithmic Issues The implementation of the RSA cryptosystem requires various algorithms Overall Representation of integers of arbitrarily large size and arithmetic operations on them n Encryption n Modular power Decryption n Modular power Setup Generation of random numbers with a given number of bits (to generate candidates p and q) n. Primality testing (to check that candidates p and q are prime) n. Computation of the GCD (to verify that e and f(n) are relatively prime) n. Computation of the multiplicative inverse (to compute d from e) n Numerical Alg. & Cryptography 50

Modular Power The repeated squaring algorithm speeds up the computation of a modular power ap mod n Write the exponent p in binary p = pb - 1 pb - 2 … p 1 p 0 Start with Q 1 = apb - 1 mod n Repeatedly compute Qi = ((Qi - 1)2 mod n)apb - i mod n We obtain Qb = ap mod n The repeated squaring algorithm performs O (log p) arithmetic operations Example mod 19 (18 = 10010) n Q 1 = 31 mod 19 = 3 n Q 2 = (32 mod 19)30 mod 19 = 9 n Q 3 = (92 mod 19)30 mod 19 = 81 mod 19 = 5 n Q 4 = (52 mod 19)31 mod 19 = (25 mod 19)3 mod 19 = 18 n Q 5 = (182 mod 19)30 mod 19 = (324 mod 19) mod 19 = 17 19 + 1 mod 19 = 1 n 318 p 5 - 1 1 0 0 1 0 2 p 5 - i 3 1 1 3 1 Qi 3 9 5 18 1 Numerical Alg. & Cryptography 51

Modular Inverse Theorem Given positive integers a and b, let d be the smallest positive integer such that d = ia + jb for some integers i and j. We have d = gcd(a, b) Example n n n a = 21 b = 15 d=3 i = 3, j = -4 3 = 3 21 + (-4) 15 = 63 - 60 = 3 Given positive integers a and b, the extended Euclid’s algorithm computes a triplet (d, i, j) such that n n d = gcd(a, b) d = ia + jb To test the existence of and compute the inverse of x Zn, we execute the extended Euclid’s algorithm on the input pair (x, n) Let (d, i, j) be the triplet returned d = ix + jn Case 1: d = 1 i is the inverse of x in Zn Case 2: d > 1 x has no inverse in Zn n Numerical Alg. & Cryptography 52

Pseudoprimality Testing The number of primes less than or equal to n is about n / ln n Thus, we expect to find a prime among, O(b) randomly generated numbers with b bits each Testing whether a number is prime (primality testing) is believed to be a hard problem An integer n 2 is said to be a base-x pseudoprime if n xn - 1 mod n = 1 (Fermat’s little theorem) Composite base-x pseudoprimes are rare: n n A random 100 -bit integer is a composite base-2 pseudoprime with probability less than 10 -13 The smallest composite base-2 pseudoprime is 341 Base-x pseudoprimality testing for an integer n: n n Check whether xn - 1 mod n = 1 Can be performed efficiently with the repeated squaring algorithm Numerical Alg. & Cryptography 53

Randomized Primality Testing Compositeness witness function witness(x, n) with error probability q for a random variable x Case 1: n is prime witness w(x, n) = false Case 2: n is composite witness w(x, n) = false with probability q < 1 Algorithm Rand. Prime. Test tests whether n is prime by repeatedly evaluating witness(x, n) A variation of base- x pseudoprimality provides a suitable compositeness witness function for randomized primality testing (Rabin-Miller algorithm) Algorithm Rand. Prime. Test(n, k) Input integer n, confidence parameter k and composite witness function witness(x, n) with error probability q Output an indication of whether n is composite or prime with probability 2 -k t k/log 2(1/q) for i 1 to t x random() if witness(x, n)= true return “n is composite” return “n is prime” Numerical Alg. & Cryptography 54

Information Security message M one-way hash Numerical Alg. & Cryptography fingerprint f = H(M) 55

Outline and Reading Digital signatures n n Definition (§ 10. 2. 2) RSA signature and verification (§ 10. 2. 3) One-way hash functions n n Definition (§ 10. 3. 1) Applications (§ 10. 3. 2) Key distribution n n Certificates (§ 10. 3. 5) Revocation (§ 10. 3. 5) Numerical Alg. & Cryptography 56

Digital Signature A digital signature is a string S associated with a message M and the author A of M that has the following properties Integrity: S establishes that M has not been altered Nonrepudiation: S unequivocally identifies the author A of M and proves that A did indeed sign M A digital signature scheme provides algorithms for n n Signing a message by the author Verifying the signature of a message by the reader A recently passed law in the US gives digital signatures the same validity of handwritten signatures A public-key cryptosystem yields a digital signature scheme provided encrypt(KE, decrypt(KD, M)) = M Signature: Alice (author) computes S = decrypt(KD, M) using her private key KD and sends the pair (M, S) to Bob Verification: Bob (reader) computes M´ = encrypt(KE, S) using Alice’s public key KE and checks that M´ = M Numerical Alg. & Cryptography 57

RSA Digital Signature Setup: n n n Setup: n = pq, with p and q primes e relatively prime to f(n) = (p - 1) (q - 1) d inverse of e in Zf(n) Keys: n n Public key: KE = (n, e) Private key: KD = d Signature: n n Message M in Zn Signature S = Md mod n Verification: n n p = 5, q = 11 n = 5 11 = 55 f(n) = 4 10 = 40 e=3 d = 27 (3 27 = 81 = 2 40 + 1) Keys: n n Public key: KE = (55, 3) Private key: KD = 27 Signature: n n M = 51 S = 5127 mod 55 = 6 Verification: Check that M = Se mod n n S = 63 mod 55 = 216 mod 55 = 51 Numerical Alg. & Cryptography 58

One-Way Hash Function A one-way hash function is a function H with the following properties n n n M maps a string M of arbitrary length into an integer f = H(M) with a fixed number of bits, called the fingerprint or digest of M H can be computed efficiently Given an integer f, it is computationally infeasible to find a string M such that H(M) = d Given a string M , it is computationally infeasible to find another string M´ such that H(M) = H(M´) (collision resistance) It is computationally infeasible to find two strings M and M´ such that H(M) = H(M´) (strong collision resistance) Two widely used one-way hash functions are n n MD 5 (Message Digest 5, 1992), which uses a 128 -bit (16 bytes) fingerprint SHA-1 (Secure Hash Algorithm 1, 1995), which uses a 160 -bit (20 bytes) fingerprint Numerical Alg. & Cryptography 59

Coin Flipping Over the Net Alice and Bob want to flip a random coin by communicating over the internet The following protocol, based on a one-way hash function H, ensures the fairness of the outcome n n n Alice picks a random integer x, computes the fingerprint f = H(x) and sends f to Bob sends to Alice his guess of whether x is odd or even Alice announces the result of the coin flip: heads if Bob has guessed correctly and tails otherwise Alice sends to Bob integer x as a proof of the outcome of the flip Bob verifies that f = H(x) Because of the strong-collision resistance property, it is computationally infeasible for Alice to cheat Numerical Alg. & Cryptography 60

Digitally Signed Fingerprints In the RSA digital signature scheme with modulus n, the message to be signed must be an integer in Zn , i. e. , the message should have at most b = log n bits To overcome the above restriction on the message length, we can use the fingerprint f = H(M) of the message instead of the message itself, where H is a one-way hash function n n Alice computes first f = H(M) and then the signature S of f Bob first computes f = H(M) and then verifies S Since the one-way hash function H has the collision-resistance property, it is computationally infeasible to modify the message M while preserving the signature of the fingerprint f = H(M) message M one-way hash fingerprint f = H(M) Numerical Alg. & Cryptography signature S = f d mod n 61

Certificates Public-key cryptography is based on the knowledge by each participant of the public key of the other participants It is complicated to securely distribute the public keys of all the participants A certificate is a message of the type (name, public key) signed by a third-party Public-key infrastructure (PKI) n n n An entity trusted by all the participants, called certification authority (CA), issues to each participant a certificate (Name, KE) that authoritatively binds the participants to their public keys Only the CA’s public key needs to be distributed securely Before sending an encrypted message to Bob or verifying a message digitally signed by Bob, Alice determines Bob’s public key KE by using Bob’s certificate (Bob, KE) Numerical Alg. & Cryptography 62

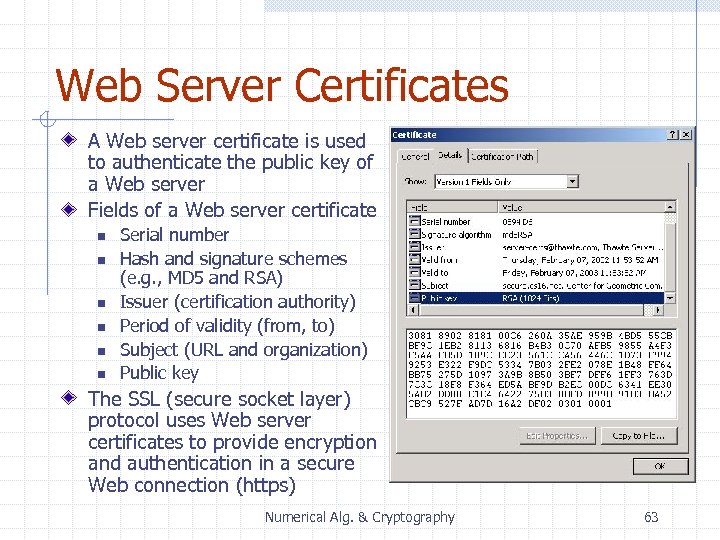Web Server Certificates A Web server certificate is used to authenticate the public key of a Web server Fields of a Web server certificate n n n Serial number Hash and signature schemes (e. g. , MD 5 and RSA) Issuer (certification authority) Period of validity (from, to) Subject (URL and organization) Public key The SSL (secure socket layer) protocol uses Web server certificates to provide encryption and authentication in a secure Web connection (https) Numerical Alg. & Cryptography 63

Certificate Revocation In certain circumstances, a certificate may have to be revoked before its expiration date n n The private key of the subject has been compromised The certificate was incorrectly issued by the CA Certificate Revocation List (CRL) n n Time-stamped list of all the unexpired certificates that have been revoked by the CA Periodically published and signed by the CA When presented with a certificate, one should n n Verify the CA’s signature on the certificate Check that the certificate has non been revoked by searching in the latest available CRL By default, Web browsers do not check the revocation status of a Web server certificate, which poses a security risk Numerical Alg. & Cryptography 64