7b00966dbd6d9d580403ebf60a5c5e7e.ppt
- Количество слайдов: 27

Numeracy Parent Information Session

Outline Problem Solving Activity How is Mathematics taught now? The New Zealand Numeracy Framework and the different stages Helpful and practical ideas to support your child’s learning in mathematics. Mathletics Game Time

Question Time There are 47 children in the hall. 28 more children arrive. How many are in the school hall now? How did you work it out? What happened in your head? Share your different strategies with the people around you

Make sense of these Strategies “Four rows of ten is 40 and two rows of ten is 20, so 40 + 20 = 60 with 7 and 8 left ! double 7 = 14 plus 1 =15 so there are 75 children” “I use an open number line!” +3 +20 47 47 + 28 = +5 75 “I know that 50 plus 30 is 80 and 3 plus 2 is 5, so 80 - 5 is 75 “ “I use tidy numbers: 50 + 28 = 78 78 - 3 = 75”. “I think of 47 +28 7 plus 8 is 15, so that’s 5 and carry one. 4 plus 2 is 6 plus one more ten is 7. so the answer is 75”

Numeracy Project Goal “to be numerate is to have the ability and inclination to use mathematics effectively – at home, at work and in the community” Published in Curriculum Update 45:

Goals Developing multiple flexible thinking strategies Mental and oral forms before written standard vertical forms Make decisions about the smartest strategy to use on any given problem. Challenge children to achieve and develop a positive attitude towards learning mathematics.
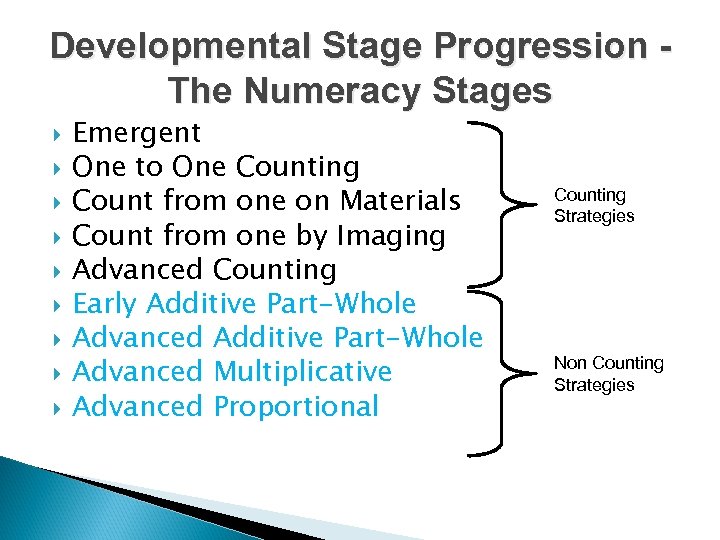
Developmental Stage Progression The Numeracy Stages Emergent One to One Counting Count from one on Materials Count from one by Imaging Advanced Counting Early Additive Part-Whole Advanced Multiplicative Advanced Proportional Counting Strategies Non Counting Strategies

Emergent Stage Zero Can you get me 7 counters from the pile please? 1, 2, 3, 5, 8…? Movie Clip Children at this stage can not consistently count a collection of objects.

Stage One to One Counting Can you get me 7 counters from the pile please? 1, 2, 3, 4, 5, 6, 7 Children at Stage One can count a set of objects up to ten but can’t join and separate sets like 4 + 3 =

Stage Count From One on Two Materials There are 5 counters and another 4 counters. How many are there altogether? 1, 2, 3, 4, 5, 6, 7, 8, 9 Children at Stage Two solve problems by using their fingers or other materials, always counting from one.

Stage Count From One By Three Imaging There are 5 counters and another 3 counters. How many are there altogether? Counts in head 1, 2, 3, 4, 5, 6, 7, 8 Children at Stage Three count all of the objects from one by imaging the objects in their mind.

Advanced Counting. Stage Four – Counting On There are 9 counters under there and another 4 counters under there. How many are there altogether? 9. . . 10, 11, 12, 13 Counts on from 9… 10, 11, 12, 13 Children at Stage Four count on from the largest number tracking how many they have added using materials or imaging.
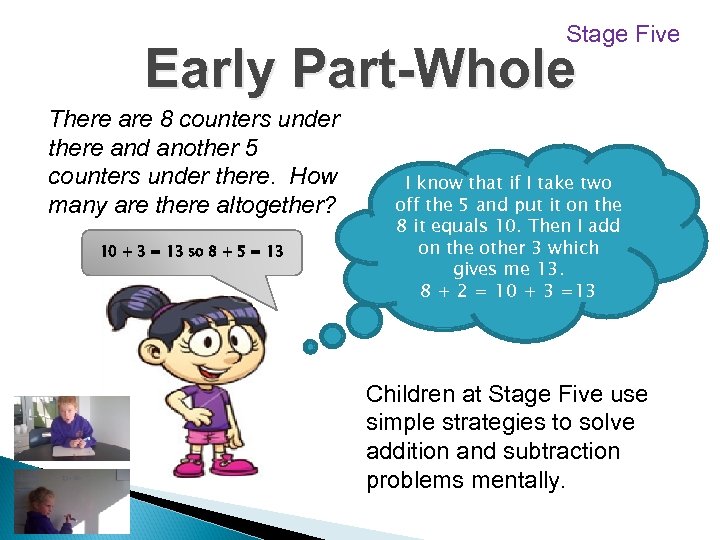
Stage Five Early Part-Whole There are 8 counters under there and another 5 counters under there. How many are there altogether? 10 + 3 = 13 so 8 + 5 = 13 I know that if I take two off the 5 and put it on the 8 it equals 10. Then I add on the other 3 which gives me 13. 8 + 2 = 10 + 3 =13 Children at Stage Five use simple strategies to solve addition and subtraction problems mentally.

Stage Six Advanced Part-Whole 63 people are on the bus and 39 people get off the bus. How many people are left on the bus? I think that tidy numbers would be the quickest way to solve this problem. I know that 63 – 40 is 23 so 63 – 39 must be 24 Children at Stage Six can select from a wide range of strategies to solve various addition and subtraction problems mentally

Stage Seven Advanced Multiplicative There are 22 fruit trees in each aisle of the orchard. There are 4 aisles. How many trees are there altogether? I think that using place value will be a quick way to solve this problem. 10 x 4 = 40 20 x 4 = 80 2 x 4 = 8 so the answer is 88. Children at Stage Seven can select from a wide range of strategies to solve various multiplication and division problems mentally.

Stage Eight Advanced Proportional You can make 9 mittens from 15 balls of wool. How many mittens can you make from 10 balls of wool? I can see that 9: 15 are both multiples of 3. I can simplify by dividing by 3 to get a ratio of 3: 5. 10 is double 5 so I then double 3 which gives me an answer of 6. Children at Stage Eight can select from a wide range of strategies to solve challenging problems involving, decimals, fraction percentages and ratios.

The NZ Numeracy Framework key Each Numeracy Stage highlights knowledge and strategy that a child should know. Strong knowledge is essential for students to broaden their strategies across a full range of numbers. Creates new knowledge through use Strategy Knowledge Provides the foundation for strategies

Knowledge and Strategy Knowledge – Number Identification, Number sequence and order, Grouping and place value, basic facts Strategy – Addition and Subtraction, Multiplication and Division, Fraction and Proportions

How maths is taught at Golden Sands School Teachers model and support children’s understanding using a researched teaching model. Using materials Thinking about what would happen on the materials Working only on numbers Teach to achieve next learning steps. Using Materials Imaging Materials Working only with numbers

Knowing where our students are at Knowledge is assessed through ◦ ◦ One on One interviews (Years 0 – 2) Timed powerpoint (Years 3 – 6) Basic Facts test through timed powerpoint (Year 1 – 6) Classroom Observation Strategy is assessed through ◦ One on One interviews with the teacher (Year 0 – 6) ◦ Classroom Observation

How can you help your child’s Numeracy development? A key to your child’s success with their Numeracy is the development of their knowledge.

Building your child’s knowledge Counting – forwards and backwards (cars, shells on beach, pegs, run around the house, how many steps you walk, count backwards, start from different numbers) Numbers before and after (Letter boxes, say a number, use a numberline, use number cards, write a number down, ladder game, keyboard numbers, using dice) Reading and identifying numbers (Letter boxes, number plates, speed signs, how many km to go, number cards, combine numbers) Ordering numbers (Number cards, write some numbers down)

Building your child’s knowledge Knowing groups to ten (Using ten frames, using fingers) Basic addition facts to ten (Buttons, ten frames, fingers) Recalling Doubles (ten frames, fingers) Ten frames

Mathletics Two main areas for student learning ◦ Curriculum Activities – Building Strategy and Strand. ◦ Live Mathletics – Building instant recall of basic facts. www. mathletics. co. nz

Part-Whole Thinkers To become Part-Whole thinkers children need automatic recall of … Facts to Ten Double Facts Ten and facts…. 10 + 6 = 16 To become Multiplicative thinkers children need to be able to recall of their timetables

Game Time Have a go at each of the activities around the room. These activities will encourage the development of knowledge. In your pack to take home you will find copies of all of the activities that are around the room.

Thanks for your support with your child/children’s Numeracy development.
7b00966dbd6d9d580403ebf60a5c5e7e.ppt