a8c363a60eec2fb0769a28ca3d67657e.ppt
- Количество слайдов: 82

Null-field approach for multiple circular inclusion problems in anti-plane piezoelectricity Reporter: An-Chien Wu Advisor: Jeng-Tzong Chen Date: 2006/06/29 Place: HR 2 307 National Taiwan Ocean University MSVLAB Department of Harbor and River Engineering 94學年度第 2學期碩士論文口試 1

Outline • Motivation and literature review • Unified formulation of null-field approach ◎ Boundary integral equations and null-field integral equations ◎ Adaptive observer system ◎ Linear algebraic equation ◎ Vector decomposition technique • Numerical examples • Conclusions • Further studies MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 2

Outline • Motivation and literature review • Unified formulation of null-field approach ◎ Boundary integral equations and null-field integral equations ◎ Adaptive observer system ◎ Linear algebraic equation ◎ Vector decomposition technique • Numerical examples • Conclusions • Further studies MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 3
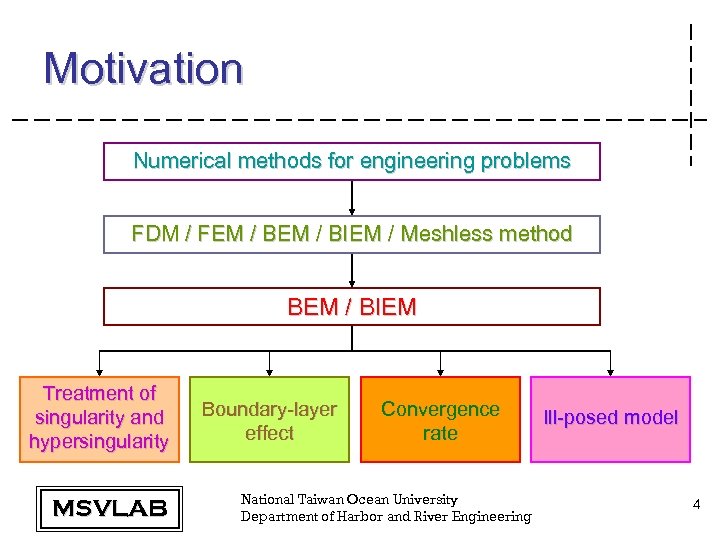
Motivation Numerical methods for engineering problems FDM / FEM / BIEM / Meshless method BEM / BIEM Treatment of singularity and hypersingularity MSVLAB Boundary-layer effect Convergence rate National Taiwan Ocean University Department of Harbor and River Engineering Ill-posed model 4
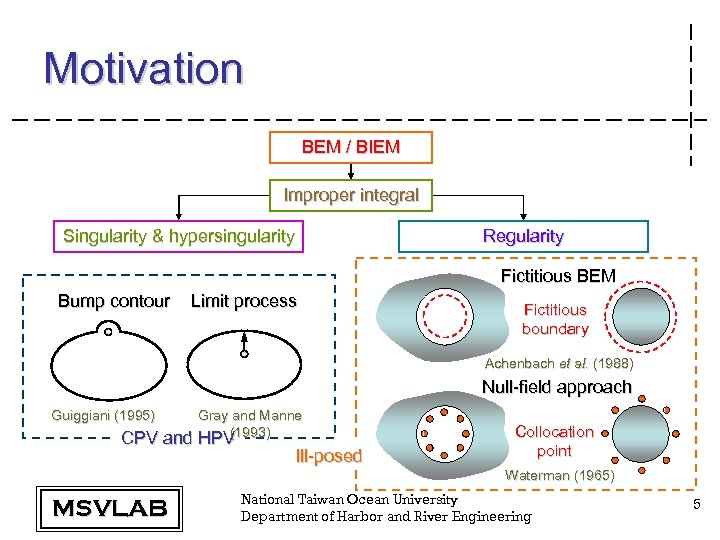
Motivation BEM / BIEM Improper integral Singularity & hypersingularity Regularity Fictitious BEM Bump contour Limit process Fictitious boundary Achenbach et al. (1988) Null-field approach Guiggiani (1995) Gray and Manne (1993) HPV CPV and HPV Ill-posed Collocation point Waterman (1965) MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 5
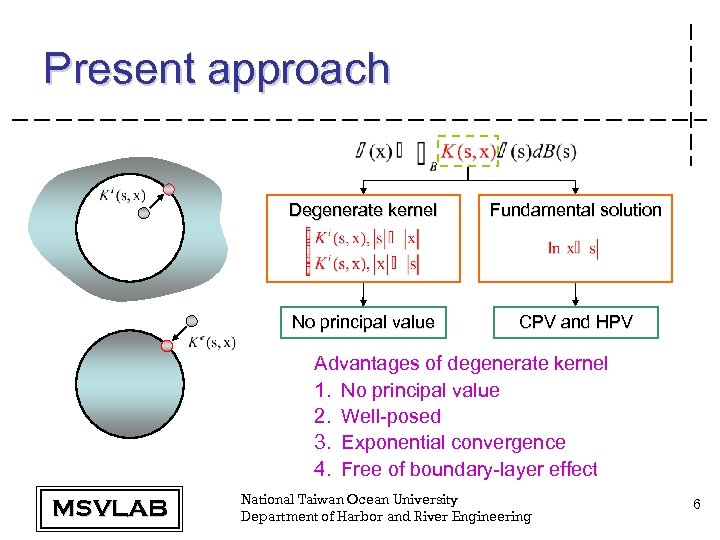
Present approach Degenerate kernel Fundamental solution No principal value CPV and HPV Advantages of degenerate kernel 1. No principal value 2. Well-posed 3. Exponential convergence 4. Free of boundary-layer effect MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 6
![Engineering problem with holes, inclusions and cracks [Chebyshev polynomial] Degenerate boundary Straight boundary [Legendre Engineering problem with holes, inclusions and cracks [Chebyshev polynomial] Degenerate boundary Straight boundary [Legendre](https://present5.com/presentation/a8c363a60eec2fb0769a28ca3d67657e/image-7.jpg)
Engineering problem with holes, inclusions and cracks [Chebyshev polynomial] Degenerate boundary Straight boundary [Legendre polynomial] [Mathieu function] Elliptic hole Circular inclusion [Fourier series] MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 7

Literature review – analytical solutions for problems with circular boundaries Key point Main application Author Conformal mapping Torsion problem In-plane electrostatics Anti-plane elasticity Chen & Weng (2001) Emets & Onofrichuk (1996) Budiansky & Carrier (1984) Steif (1989) Wu & Funami (2002) Wang & Zhong (2003) Bi-polar coordinate Electrostatic potential Elasticity Lebedev et al. (1965) Howland & Knight (1939) Möbius transformation Anti-plane piezoelectricity & elasticity Honein et al. (1992) Complex potential approach Anti-plane piezoelectricity Wang & Shen (2001) Those analytical methods are only limited to doubly connected regions even to conformal connected regions. MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 8
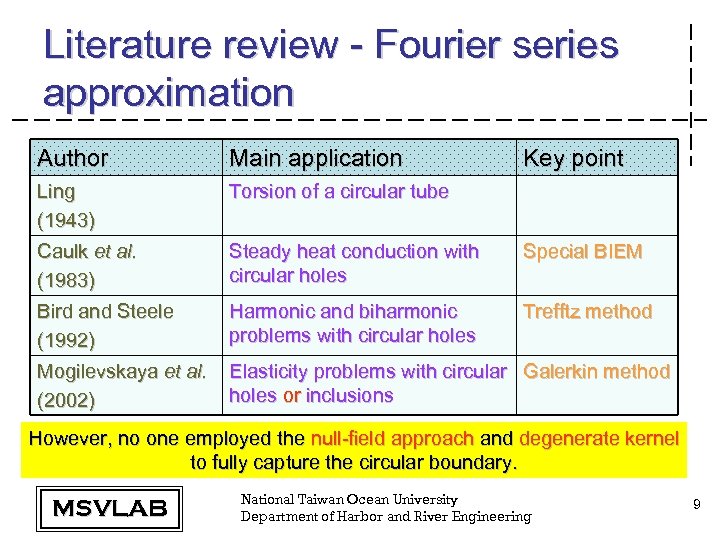
Literature review - Fourier series approximation Author Main application Key point Ling (1943) Torsion of a circular tube Caulk et al. (1983) Steady heat conduction with circular holes Special BIEM Bird and Steele (1992) Harmonic and biharmonic problems with circular holes Trefftz method Mogilevskaya et al. (2002) Elasticity problems with circular Galerkin method holes or inclusions However, no one employed the null-field approach and degenerate kernel to fully capture the circular boundary. MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 9

Outline • Motivation and literature review • Unified formulation of null-field approach ◎ Boundary integral equations and null-field integral equations ◎ Adaptive observer system ◎ Linear algebraic equation ◎ Vector decomposition technique • Numerical examples • Conclusions • Further studies MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 10

Boundary integral equation and null -field integral equation Interior case Exterior case Degenerate (separate) form MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 11

Expansions of fundamental solution and boundary density Degenerate kernel – fundamental solution Fourier series expansion – boundary density MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 12
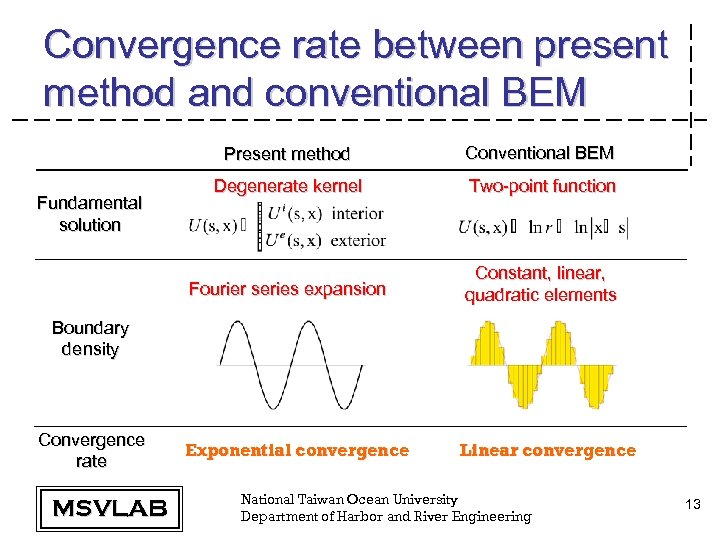
Convergence rate between present method and conventional BEM Present method Degenerate kernel Two-point function Fourier series expansion Fundamental solution Conventional BEM Constant, linear, quadratic elements Exponential convergence Linear convergence Boundary density Convergence rate MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 13

Degenerate (separate) form of fundamental solution (2 -D) MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 14

Outline • Motivation and literature review • Unified formulation of null-field approach ◎ Boundary integral equations and null-field integral equations ◎ Adaptive observer system ◎ Linear algebraic equation ◎ Vector decomposition technique • Numerical examples • Conclusions • Further studies MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 15
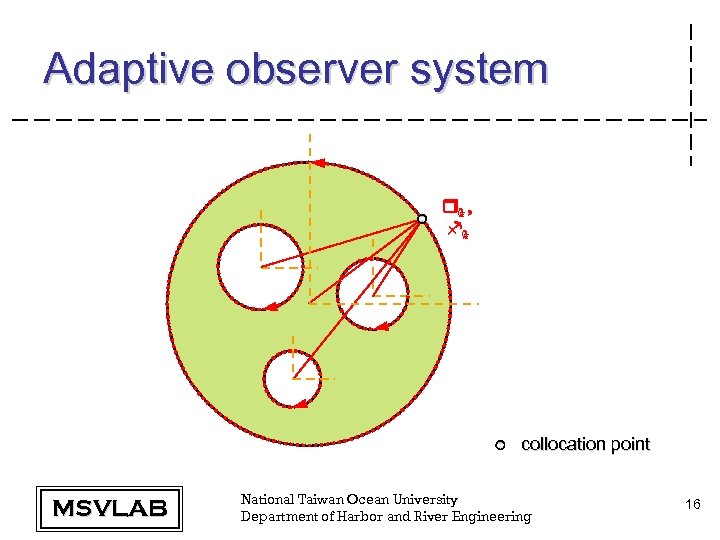
Adaptive observer system r 0 , 2 1 k f 0 2 1 k collocation point MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 16

Outline • Motivation and literature review • Unified formulation of null-field approach ◎ Boundary integral equations and null-field integral equations ◎ Adaptive observer system ◎ Linear algebraic equation ◎ Vector decomposition technique • Numerical examples • Conclusions • Further studies MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 17
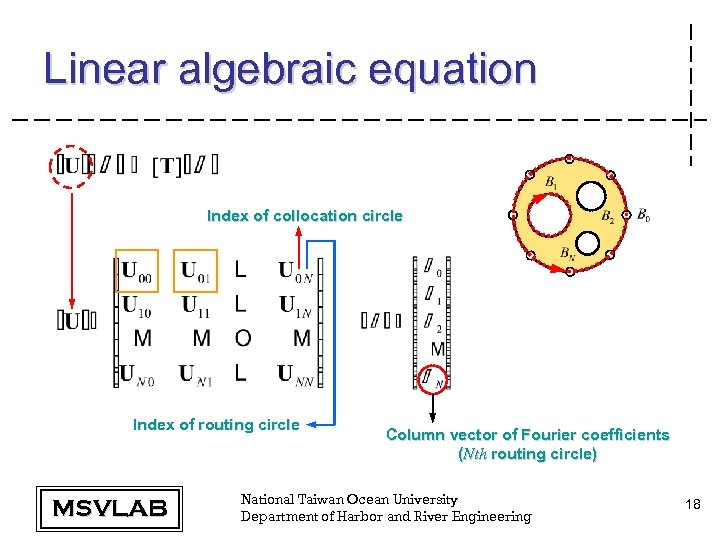
Linear algebraic equation Index of collocation circle Index of routing circle MSVLAB Column vector of Fourier coefficients (Nth routing circle) National Taiwan Ocean University Department of Harbor and River Engineering 18

Explicit form of each submatrix and vector Truncated terms of Fourier series Number of collocation points Fourier coefficients MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 19
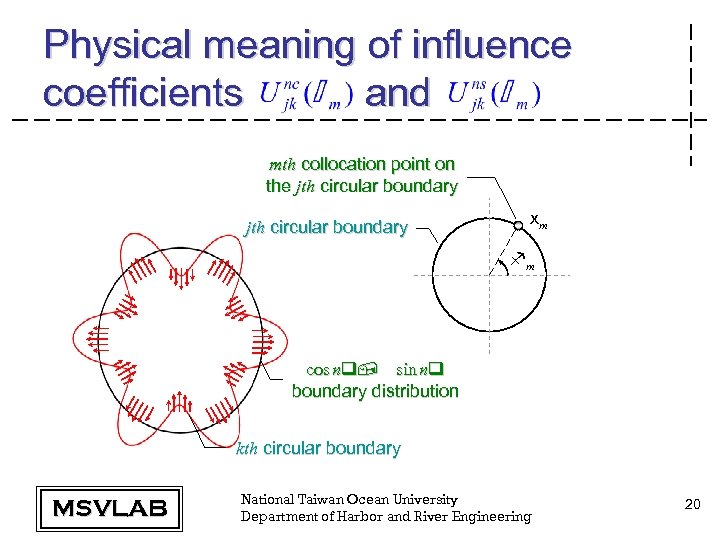
Physical meaning of influence coefficients and mth collocation point on the jth circular boundary xm fm cos nq, sin nq boundary distribution kth circular boundary MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 20

Outline • Motivation and literature review • Unified formulation of null-field approach ◎ Boundary integral equations and null-field integral equations ◎ Adaptive observer system ◎ Linear algebraic equation ◎ Vector decomposition technique • Numerical examples • Conclusions • Further studies MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 21
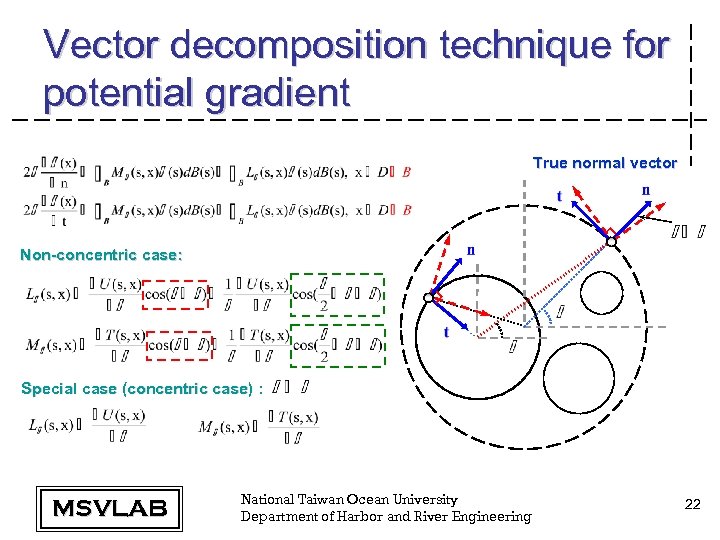
Vector decomposition technique for potential gradient True normal vector Non-concentric case: Special case (concentric case) : MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 22
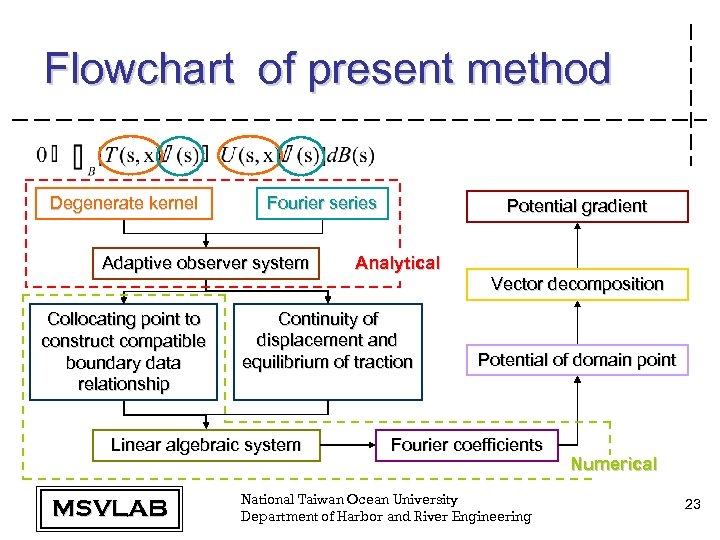
Flowchart of present method Degenerate kernel Fourier series Adaptive observer system Potential gradient Analytical Vector decomposition Collocating point to construct compatible boundary data relationship Continuity of displacement and equilibrium of traction Linear algebraic system MSVLAB Potential of domain point Fourier coefficients National Taiwan Ocean University Department of Harbor and River Engineering Numerical 23
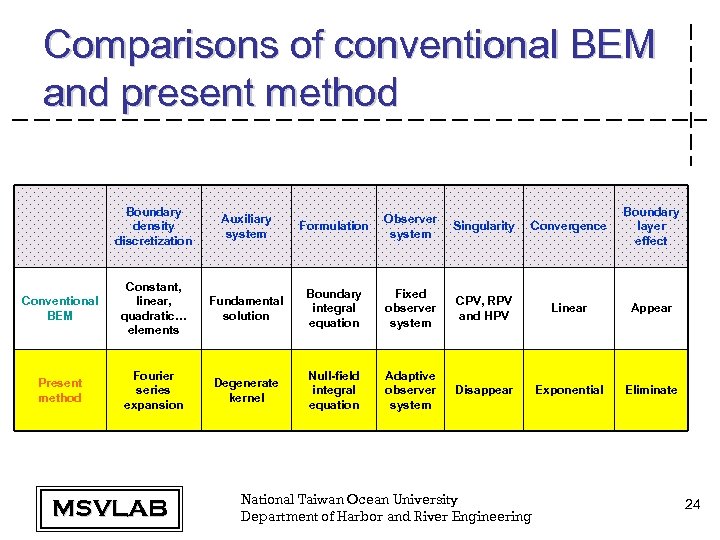
Comparisons of conventional BEM and present method Boundary density discretization Auxiliary system Formulation Observer system Singularity Convergence Boundary layer effect Conventional BEM Constant, linear, quadratic… elements Fundamental solution Boundary integral equation Fixed observer system CPV, RPV and HPV Linear Appear Present method Fourier series expansion Degenerate kernel Null-field integral equation Adaptive observer system Disappear Exponential Eliminate MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 24

Outline • Motivation and literature review • Unified formulation of null-field approach ◎ Boundary integral equations and null-field integral equations ◎ Adaptive observer system ◎ Linear algebraic equation ◎ Vector decomposition technique • • • Numerical examples Conclusions Further studies MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 25

Numerical examples • Anti-plane piezoelectricity problems (EABE, 2006, accepted) • In-plane electrostatics problems (? ? ) • Anti-plane elasticity problems (ASME-JAM, 2006, accepted) MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 26

Numerical examples • Anti-plane piezoelectricity problems • In-plane electrostatics problems • Anti-plane elasticity problems MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 27
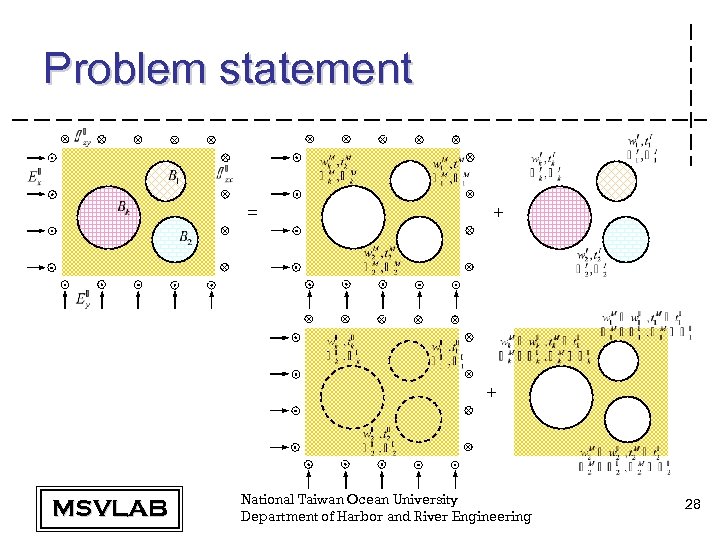
Problem statement = + + MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 28

Analogy between anti-plane deformation and inplane electrostatics for anti-plane piezoelectricity Anti-plane shear deformation Constitutive equations for anti-plane piezoelectricity In-plane electrostatics z-displacement w Electric potential F Strain gzi Electric field Ei Stress szi Shear modulus m Strain-disp. gzi = w, i Constitutive law szi = m gzi MSVLAB Coupling effect szi = c 44 gzi – e 15 Ei Di = e 15 gzi + e 11 Ei Shear modulus c 44 Piezoelectric constant e 15 Dielectric constant e 11 Electric displacement Di Dielectric constant e Electricity Ei = – F, i Constitutive law Di = e E i National Taiwan Ocean University Department of Harbor and River Engineering 29
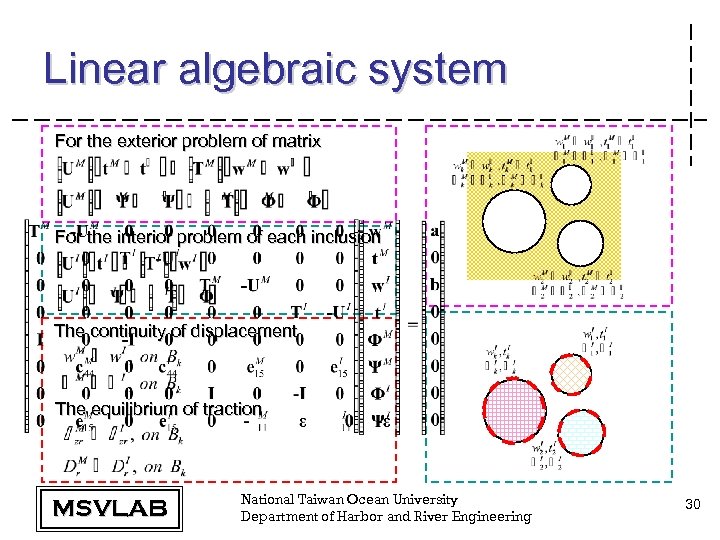
Linear algebraic system For the exterior problem of matrix For the interior problem of each inclusion The continuity of displacement The equilibrium of traction MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 30

Two circular inclusions embedded in a piezoelectric matrix under such loadings MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 31
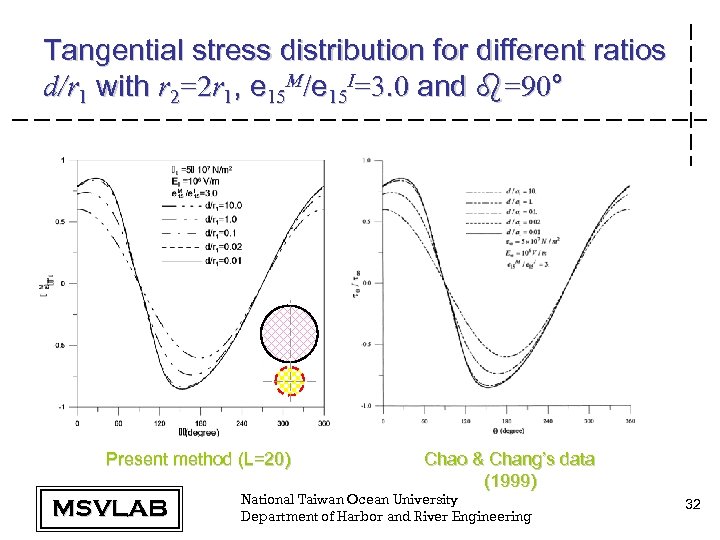
Tangential stress distribution for different ratios d/r 1 with r 2=2 r 1, e 15 M/e 15 I=3. 0 and b=90° Present method (L=20) MSVLAB Chao & Chang’s data (1999) National Taiwan Ocean University Department of Harbor and River Engineering 32
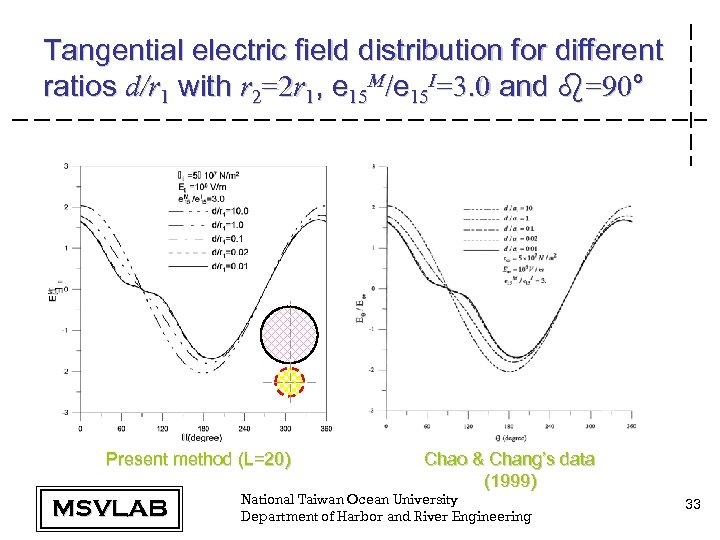
Tangential electric field distribution for different ratios d/r 1 with r 2=2 r 1, e 15 M/e 15 I=3. 0 and b=90° Present method (L=20) MSVLAB Chao & Chang’s data (1999) National Taiwan Ocean University Department of Harbor and River Engineering 33
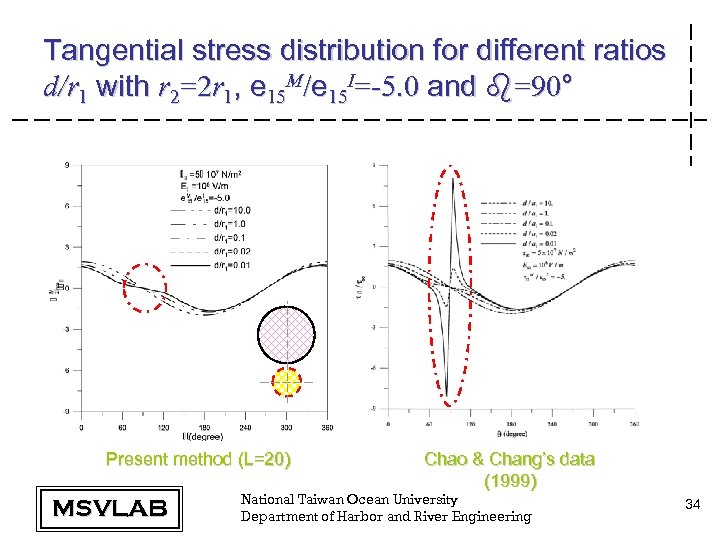
Tangential stress distribution for different ratios d/r 1 with r 2=2 r 1, e 15 M/e 15 I=-5. 0 and b=90° Present method (L=20) MSVLAB Chao & Chang’s data (1999) National Taiwan Ocean University Department of Harbor and River Engineering 34
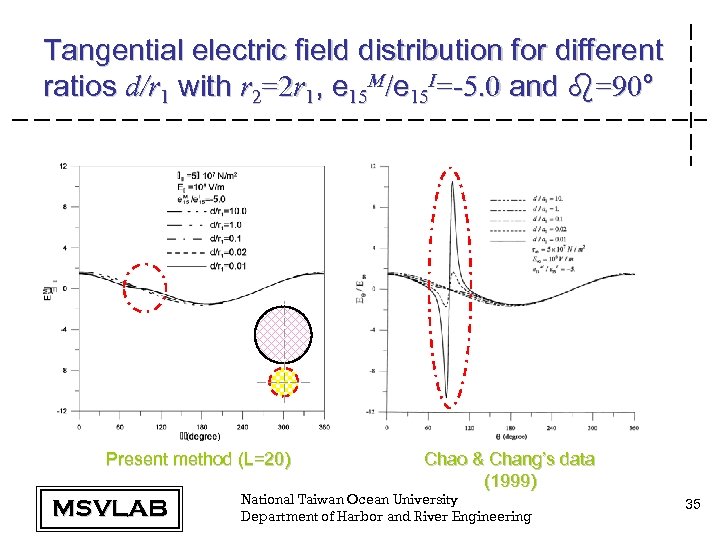
Tangential electric field distribution for different ratios d/r 1 with r 2=2 r 1, e 15 M/e 15 I=-5. 0 and b=90° Present method (L=20) MSVLAB Chao & Chang’s data (1999) National Taiwan Ocean University Department of Harbor and River Engineering 35
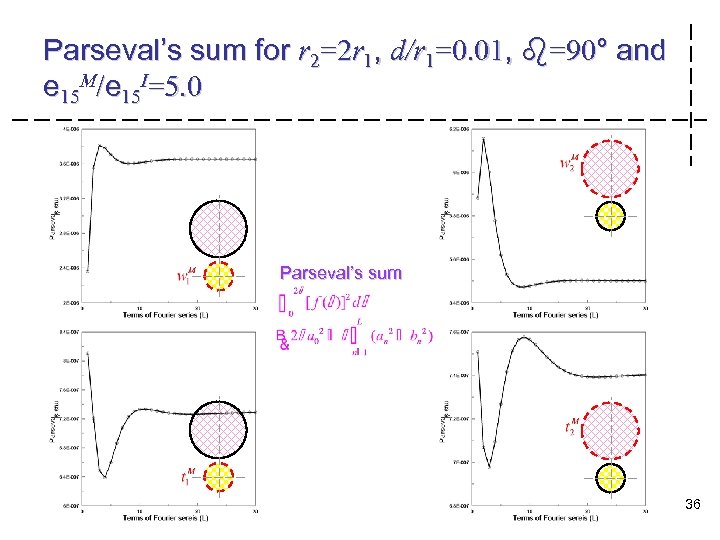
Parseval’s sum for r 2=2 r 1, d/r 1=0. 01, b=90° and e 15 M/e 15 I=5. 0 Parseval’s sum MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 36
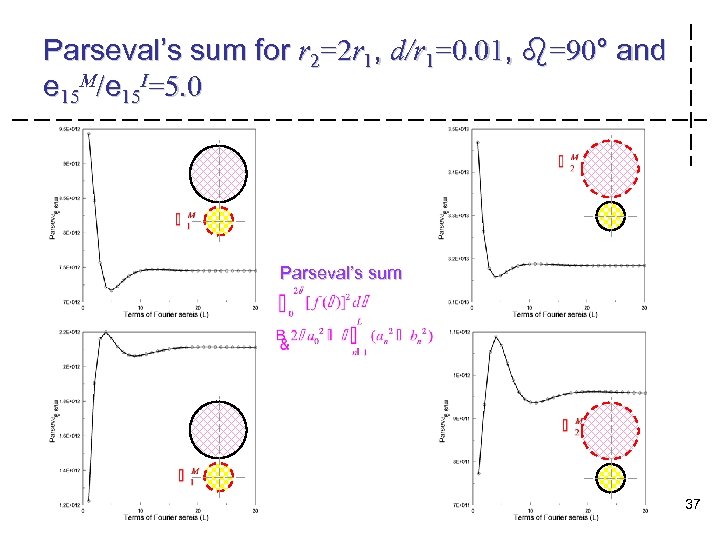
Parseval’s sum for r 2=2 r 1, d/r 1=0. 01, b=90° and e 15 M/e 15 I=5. 0 Parseval’s sum MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 37
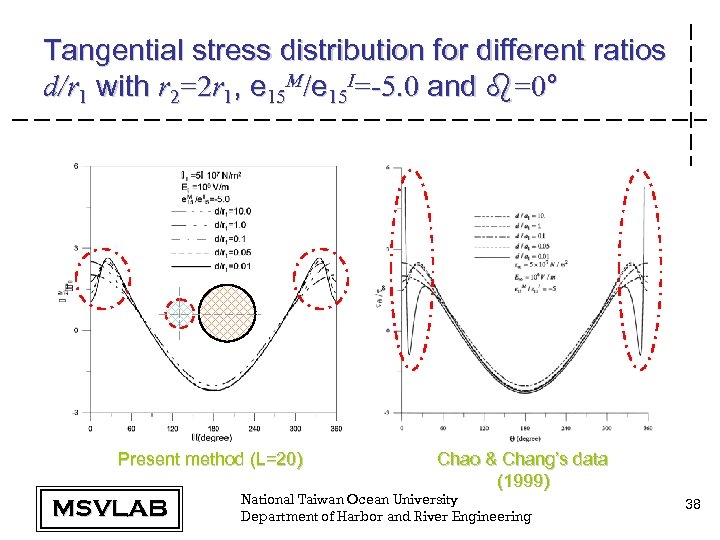
Tangential stress distribution for different ratios d/r 1 with r 2=2 r 1, e 15 M/e 15 I=-5. 0 and b=0° Present method (L=20) MSVLAB Chao & Chang’s data (1999) National Taiwan Ocean University Department of Harbor and River Engineering 38
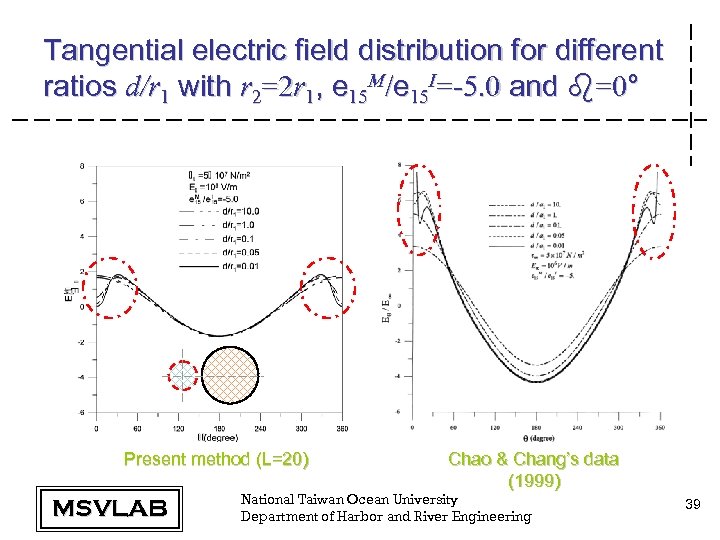
Tangential electric field distribution for different ratios d/r 1 with r 2=2 r 1, e 15 M/e 15 I=-5. 0 and b=0° Present method (L=20) MSVLAB Chao & Chang’s data (1999) National Taiwan Ocean University Department of Harbor and River Engineering 39
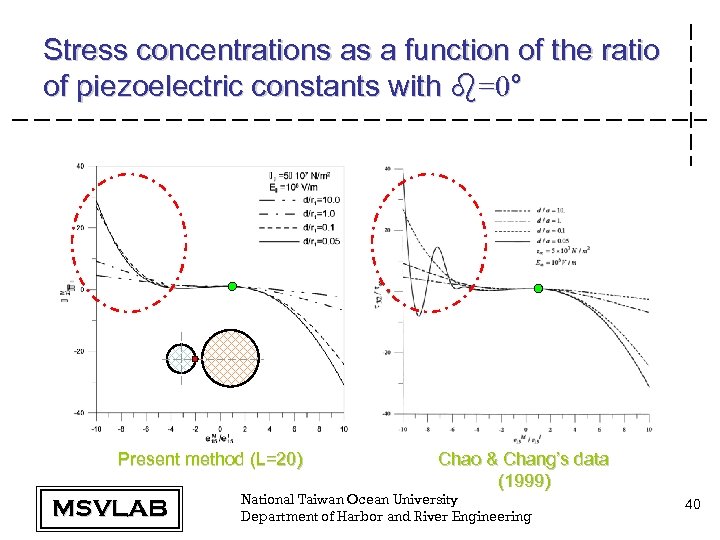
Stress concentrations as a function of the ratio of piezoelectric constants with b=0° Present method (L=20) MSVLAB Chao & Chang’s data (1999) National Taiwan Ocean University Department of Harbor and River Engineering 40
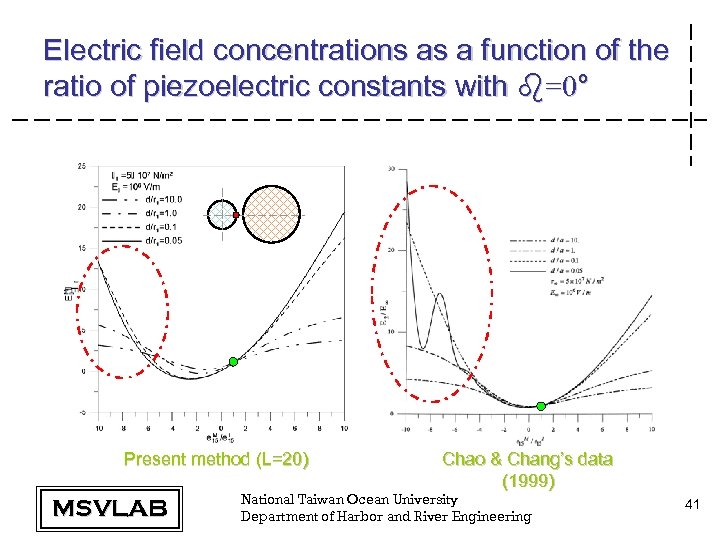
Electric field concentrations as a function of the ratio of piezoelectric constants with b=0° Present method (L=20) MSVLAB Chao & Chang’s data (1999) National Taiwan Ocean University Department of Harbor and River Engineering 41
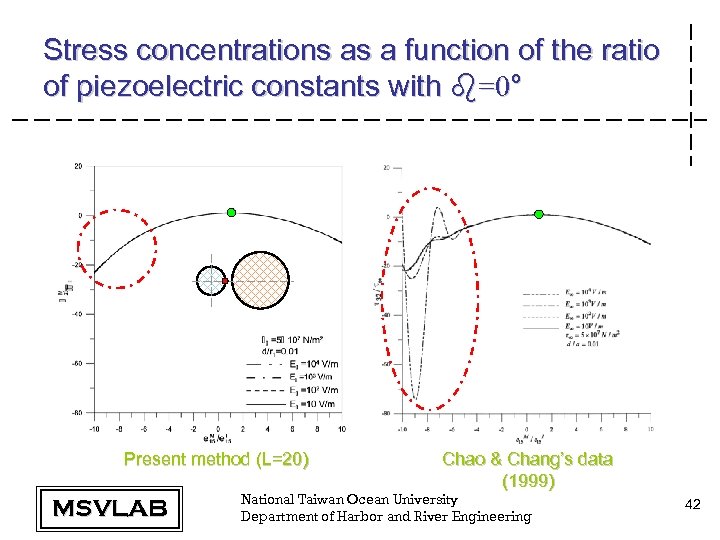
Stress concentrations as a function of the ratio of piezoelectric constants with b=0° Present method (L=20) MSVLAB Chao & Chang’s data (1999) National Taiwan Ocean University Department of Harbor and River Engineering 42
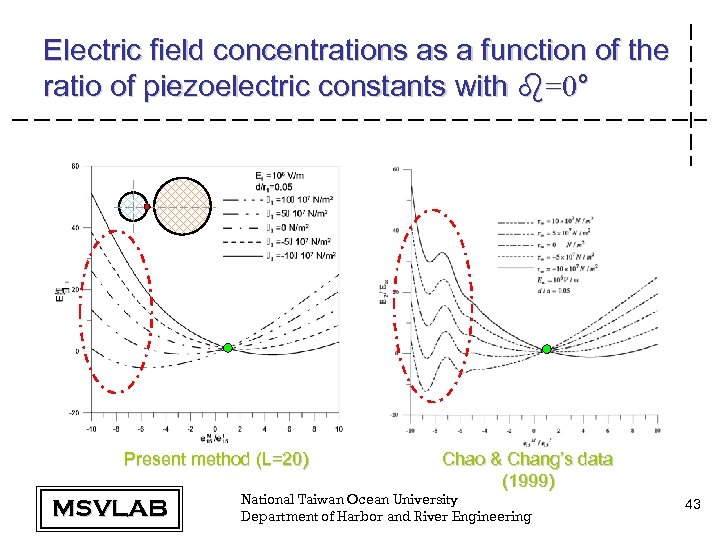
Electric field concentrations as a function of the ratio of piezoelectric constants with b=0° Present method (L=20) MSVLAB Chao & Chang’s data (1999) National Taiwan Ocean University Department of Harbor and River Engineering 43
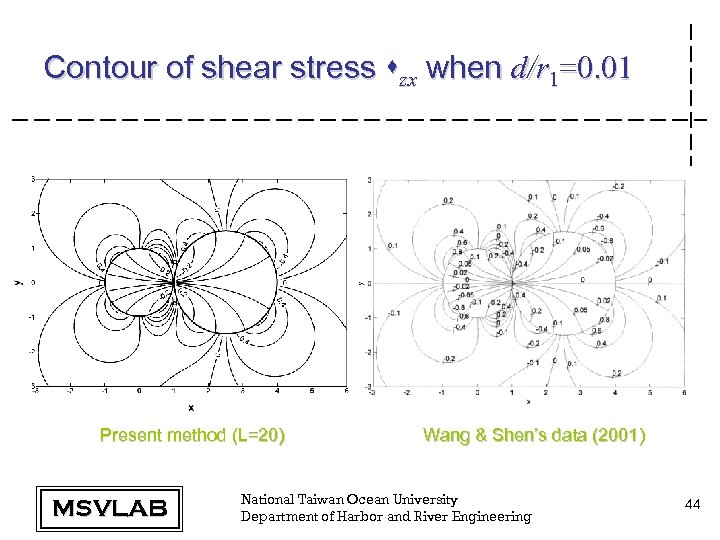
Contour of shear stress szx when d/r 1=0. 01 Present method (L=20) MSVLAB Wang & Shen’s data (2001) National Taiwan Ocean University Department of Harbor and River Engineering 44
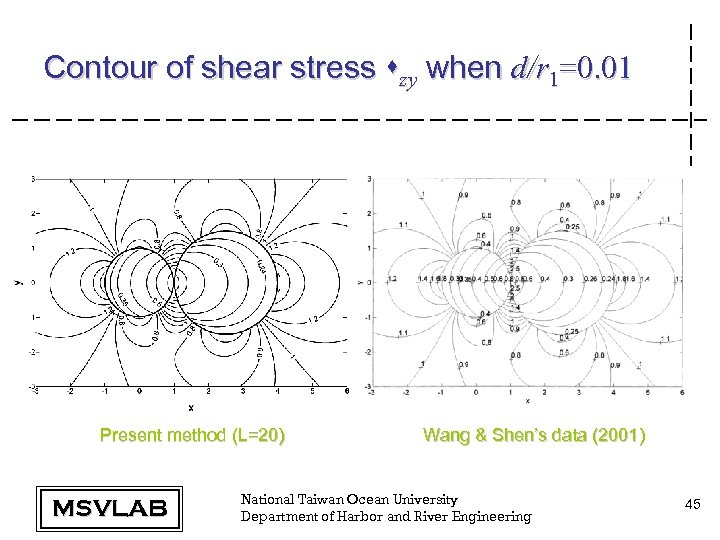
Contour of shear stress szy when d/r 1=0. 01 Present method (L=20) MSVLAB Wang & Shen’s data (2001) National Taiwan Ocean University Department of Harbor and River Engineering 45
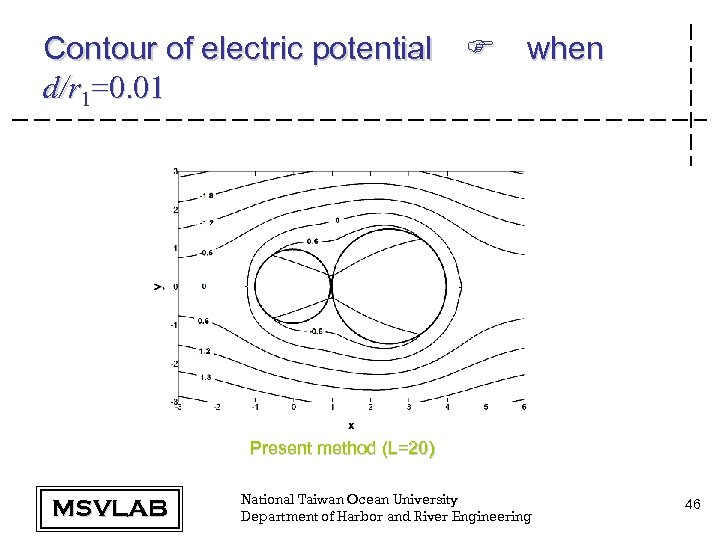
Contour of electric potential F when d/r 1=0. 01 Present method (L=20) MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 46
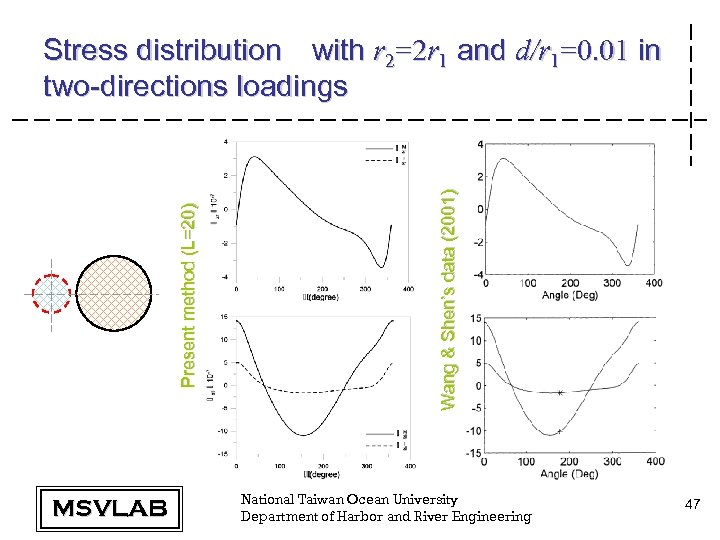
MSVLAB Wang & Shen’s data (2001) Present method (L=20) Stress distribution with r 2=2 r 1 and d/r 1=0. 01 in two-directions loadings National Taiwan Ocean University Department of Harbor and River Engineering 47
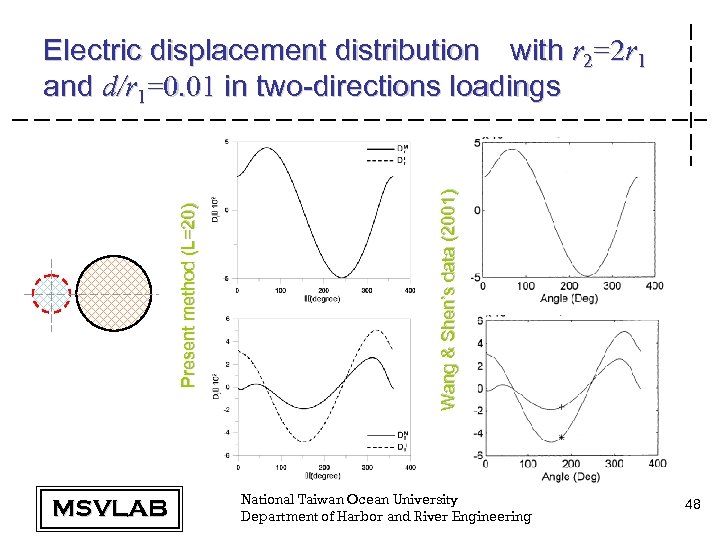
MSVLAB Wang & Shen’s data (2001) Present method (L=20) Electric displacement distribution with r 2=2 r 1 and d/r 1=0. 01 in two-directions loadings National Taiwan Ocean University Department of Harbor and River Engineering 48
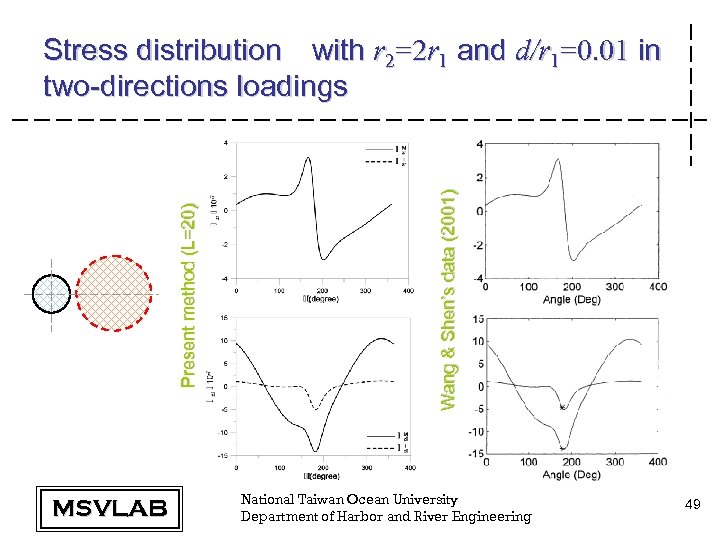
MSVLAB Wang & Shen’s data (2001) Present method (L=20) Stress distribution with r 2=2 r 1 and d/r 1=0. 01 in two-directions loadings National Taiwan Ocean University Department of Harbor and River Engineering 49
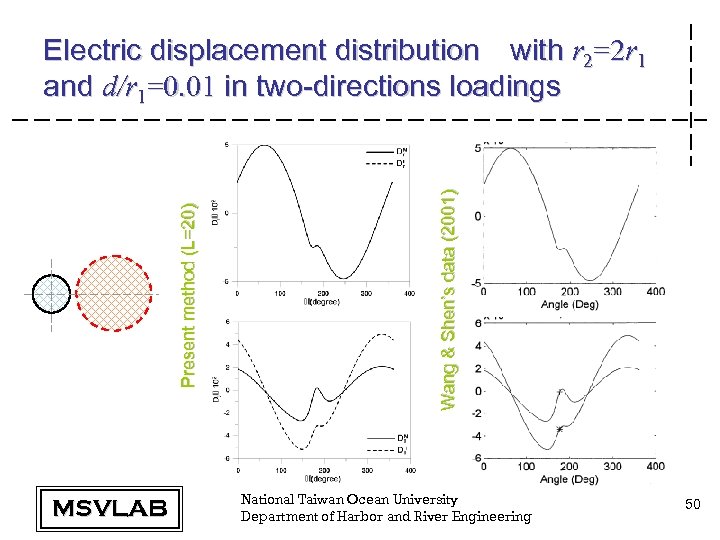
MSVLAB Wang & Shen’s data (2001) Present method (L=20) Electric displacement distribution with r 2=2 r 1 and d/r 1=0. 01 in two-directions loadings National Taiwan Ocean University Department of Harbor and River Engineering 50

Numerical examples • • • Anti-plane piezoelectricity problems In-plane electrostatics problems Anti-plane elasticity problems MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 51
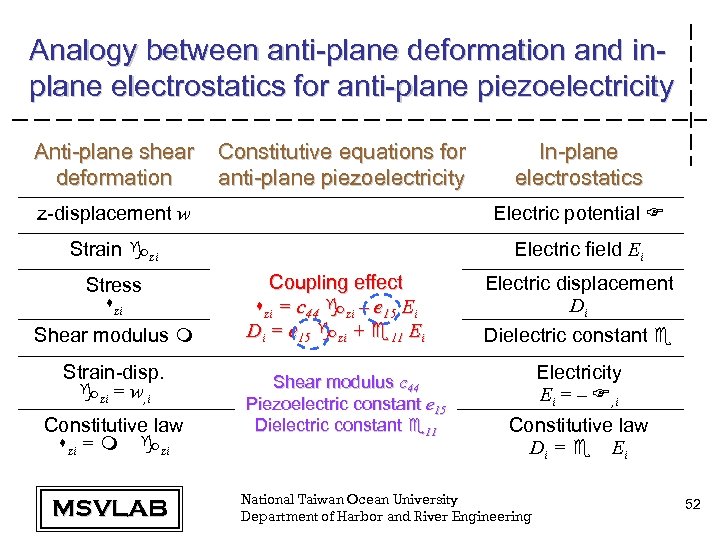
Analogy between anti-plane deformation and inplane electrostatics for anti-plane piezoelectricity Anti-plane shear deformation Constitutive equations for anti-plane piezoelectricity In-plane electrostatics z-displacement w Electric potential F Strain gzi Electric field Ei Stress szi Shear modulus m Strain-disp. gzi = w, i Constitutive law szi = m gzi MSVLAB Coupling effect szi = c 44 gzi – e 15 Ei Di = e 15 gzi + e 11 Ei Shear modulus c 44 Piezoelectric constant e 15 Dielectric constant e 11 Electric displacement Di Dielectric constant e Electricity Ei = – F, i Constitutive law Di = e E i National Taiwan Ocean University Department of Harbor and River Engineering 52
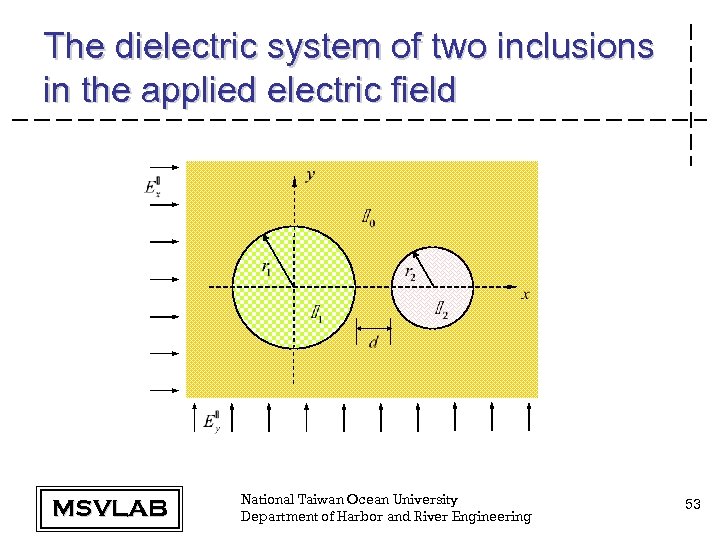
The dielectric system of two inclusions in the applied electric field MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 53
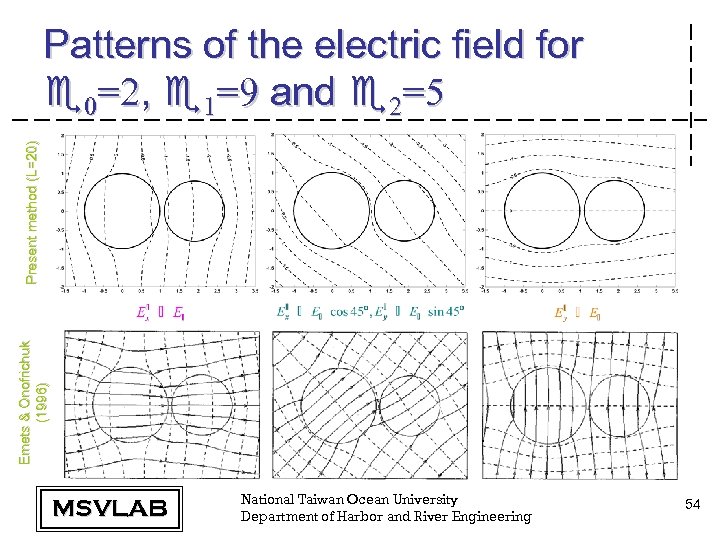
Emets & Onofrichuk (1996) Present method (L=20) Patterns of the electric field for e 0=2, e 1=9 and e 2=5 MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 54
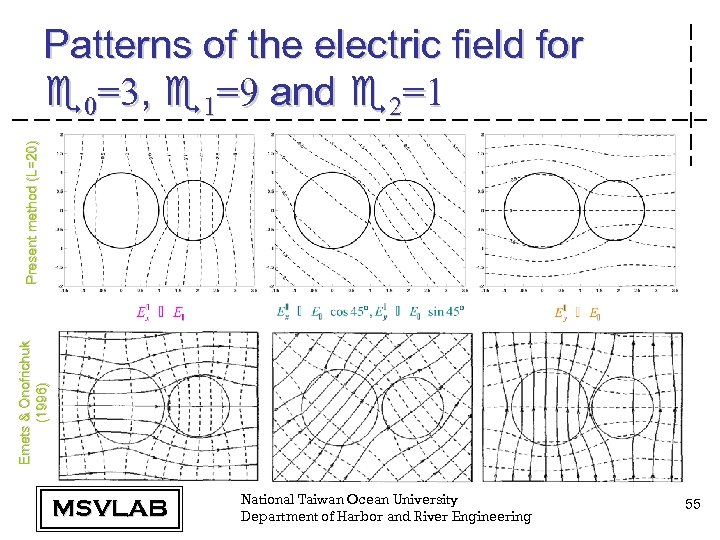
Emets & Onofrichuk (1996) Present method (L=20) Patterns of the electric field for e 0=3, e 1=9 and e 2=1 MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 55

Numerical examples • Anti-plane piezoelectricity problems • In-plane electrostatics problems • Anti-plane elasticity problems MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 56
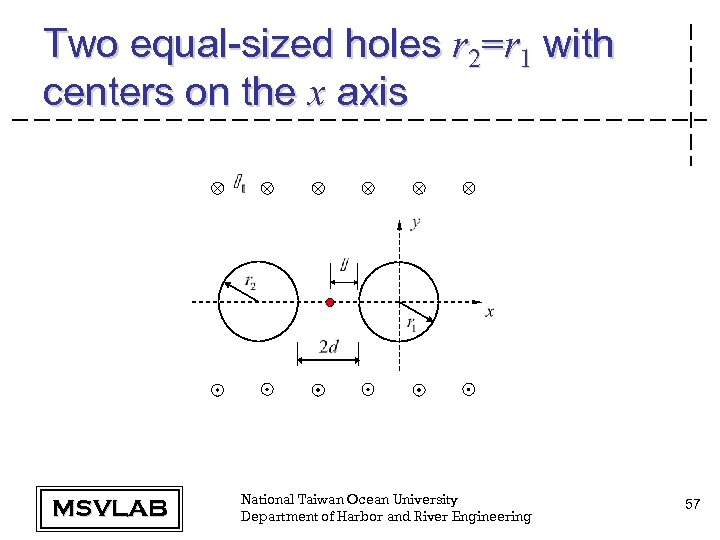
Two equal-sized holes r 2=r 1 with centers on the x axis MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 57
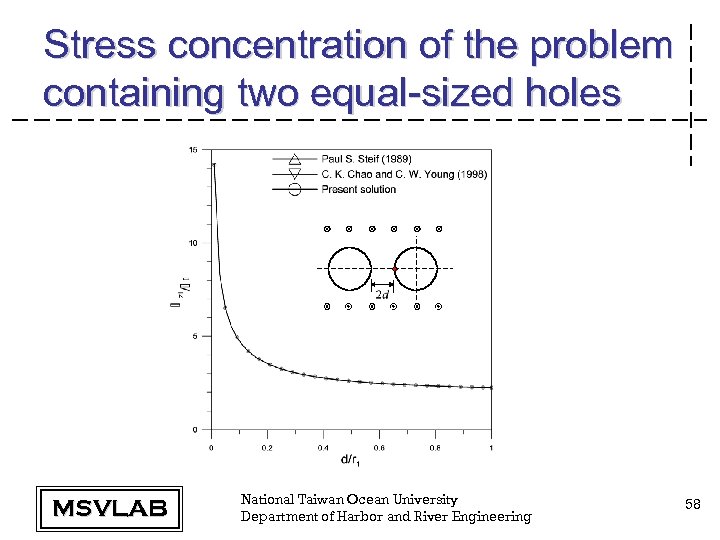
Stress concentration of the problem containing two equal-sized holes MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 58
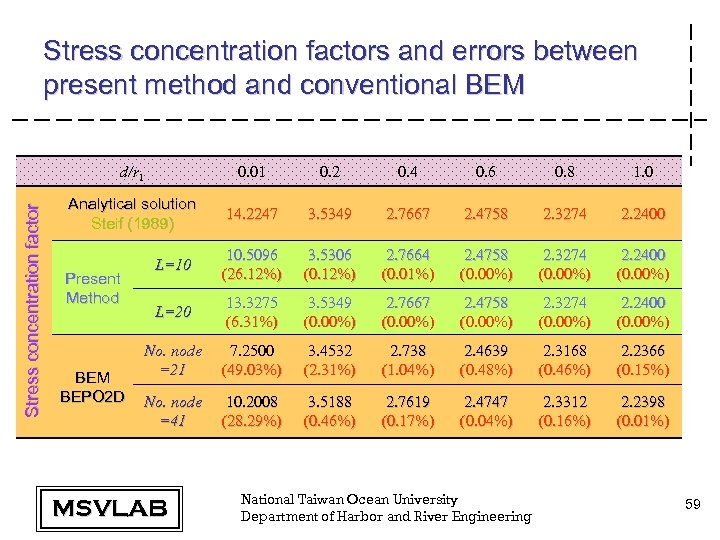
Stress concentration factors and errors between present method and conventional BEM Stress concentration factor d/r 1 0. 01 0. 2 0. 4 0. 6 0. 8 1. 0 Analytical solution Steif (1989) 14. 2247 3. 5349 2. 7667 2. 4758 2. 3274 2. 2400 L=10 10. 5096 (26. 12%) 3. 5306 (0. 12%) 2. 7664 (0. 01%) 2. 4758 (0. 00%) 2. 3274 (0. 00%) 2. 2400 (0. 00%) L=20 13. 3275 (6. 31%) 3. 5349 (0. 00%) 2. 7667 (0. 00%) 2. 4758 (0. 00%) 2. 3274 (0. 00%) 2. 2400 (0. 00%) No. node =21 7. 2500 (49. 03%) 3. 4532 (2. 31%) 2. 738 (1. 04%) 2. 4639 (0. 48%) 2. 3168 (0. 46%) 2. 2366 (0. 15%) No. node =41 10. 2008 (28. 29%) 3. 5188 (0. 46%) 2. 7619 (0. 17%) 2. 4747 (0. 04%) 2. 3312 (0. 16%) 2. 2398 (0. 01%) Present Method BEM BEPO 2 D MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 59
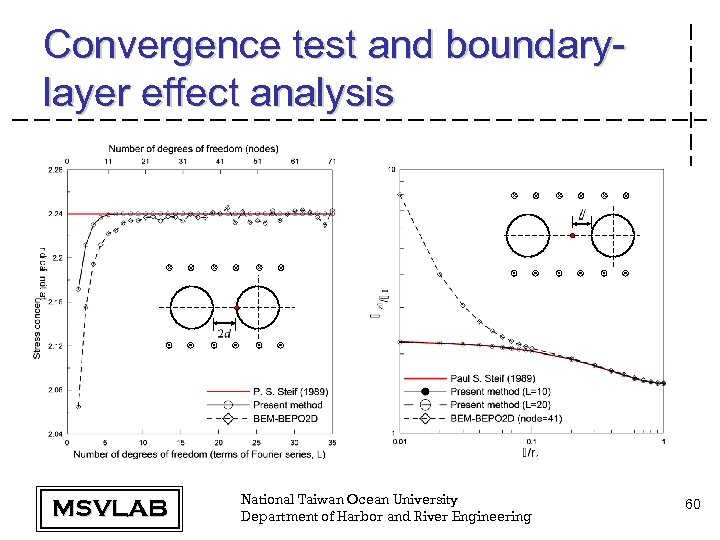
Convergence test and boundarylayer effect analysis MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 60

Two circular inclusions with centers on the y axis MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 61
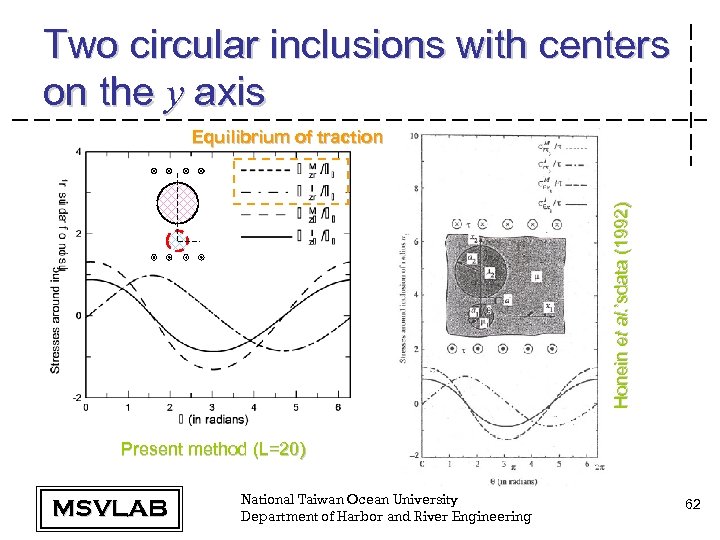
Two circular inclusions with centers on the y axis Honein et al. ’sdata (1992) Equilibrium of traction Present method (L=20) MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 62
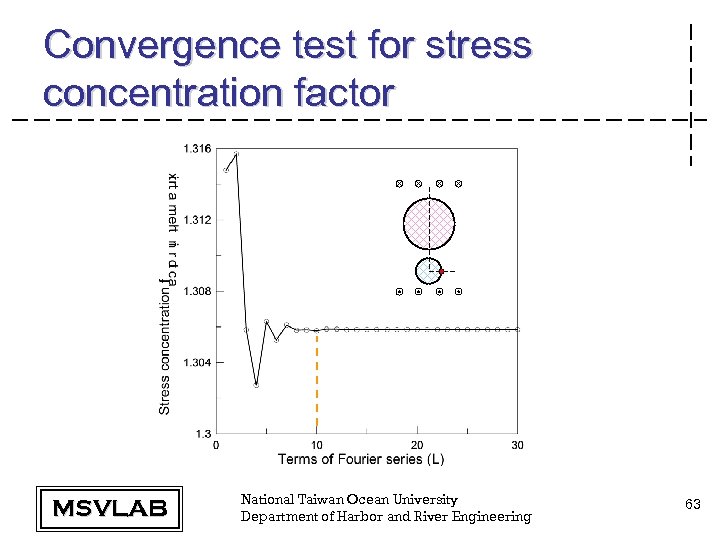
Convergence test for stress concentration factor MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 63
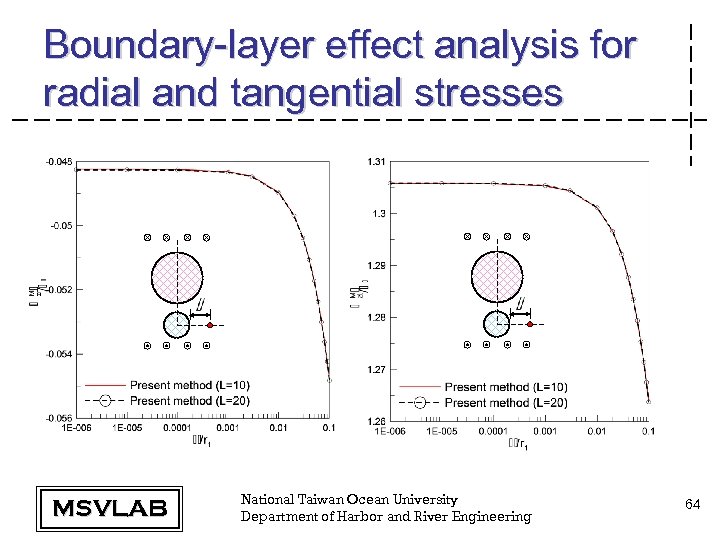
Boundary-layer effect analysis for radial and tangential stresses MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 64
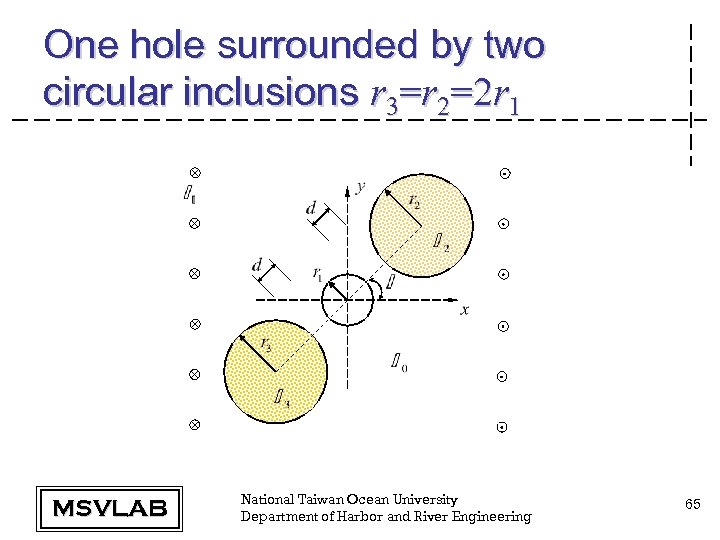
One hole surrounded by two circular inclusions r 3=r 2=2 r 1 MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 65
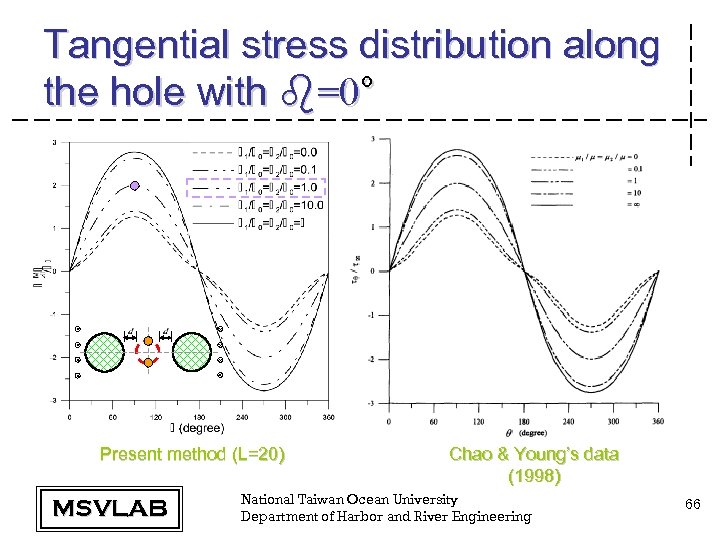
Tangential stress distribution along the hole with b=0° Present method (L=20) MSVLAB Chao & Young’s data (1998) National Taiwan Ocean University Department of Harbor and River Engineering 66
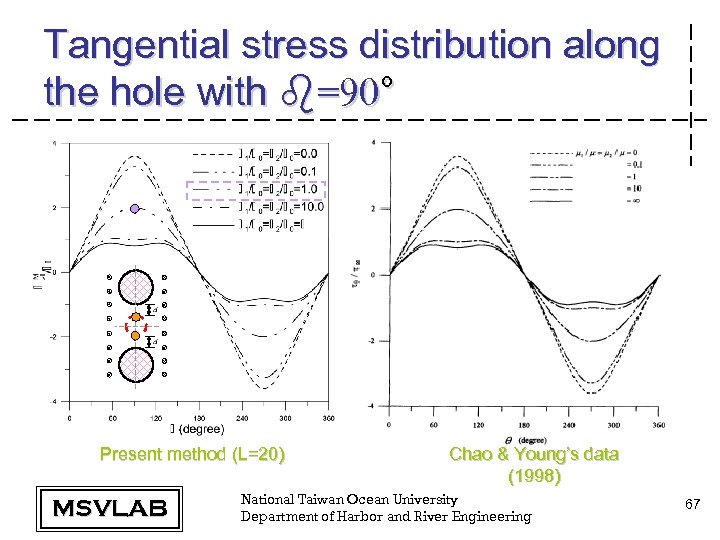
Tangential stress distribution along the hole with b=90° Present method (L=20) MSVLAB Chao & Young’s data (1998) National Taiwan Ocean University Department of Harbor and River Engineering 67
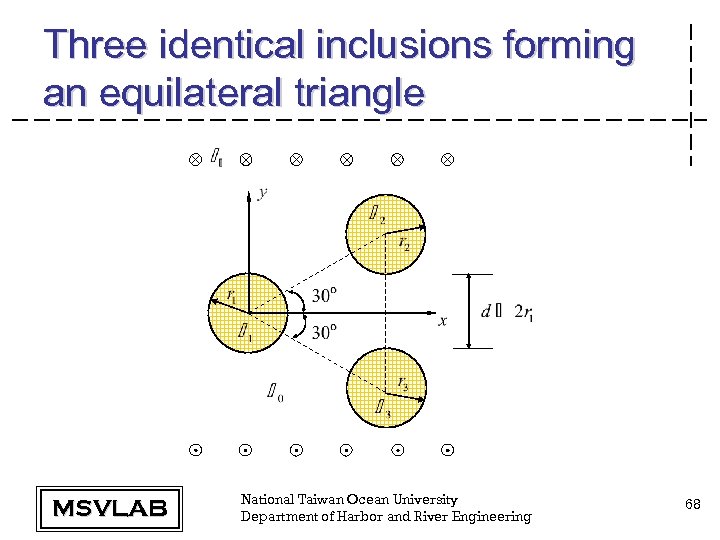
Three identical inclusions forming an equilateral triangle MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 68
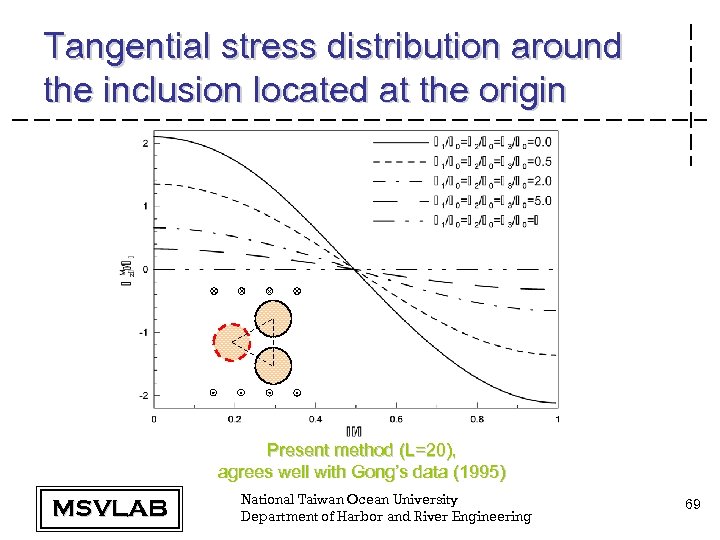
Tangential stress distribution around the inclusion located at the origin Present method (L=20), agrees well with Gong’s data (1995) MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 69

Outline • Motivation and literature review • Unified formulation of null-field approach ◎ Boundary integral equations and null-field integral equations ◎ Adaptive observer system ◎ Linear algebraic equation ◎ Vector decomposition technique • Numerical examples • Conclusions • Further studies MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 70

Conclusions • A systematic approach using degenerate kernels and Fourier series for null-field integral equation has been successfully proposed to solve BVPs with circular inclusions. • According to numerical results, only few terms of Fourier series can achieve accurate solutions. • Four goals of singularity free, boundary-layer effect free, exponential convergence and wellposed model are achieved. MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 71

Conclusions • The results demonstrate the superiority of present method over the conventional BEM. • Our semi-analytical results may provide a datum for other researchers’ reference. • The stress and electric field concentrations are dependent on the distance between the two inclusions, the mismatch in the material constants and the magnitude of mechanical and electromechanical loadings. MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 72

Conclusions • A general-purpose program for solving Laplace problems with multiple circular inclusions of various radii, arbitrary positions and different material constants was developed. • Its possible applications in engineering are very broad, not only limited in this thesis. MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 73

Outline • Motivation and literature review • Unified formulation of null-field approach ◎ Boundary integral equations and null-field integral equations ◎ Adaptive observer system ◎ Linear algebraic equation ◎ Vector decomposition technique • Numerical examples • Conclusions • Further studies MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 74

Further studies • • • Extension to general boundaries. 2 -D problems to 3 -D problems. Various loading types, e. g. concentrated forces, screw dislocations, torques, inplane shears and tensions. • Various inhomogeneous types, e. g. coated fibers and inclusions with imperfect interfaces. MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 75

The end Thanks for your kind attention. Your comments will be highly appreciated. Welcome to the web site of MSVLAB: http: //ind. ntou. edu. tw/~msvlab MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 76

Derivation of degenerate kernels MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 77
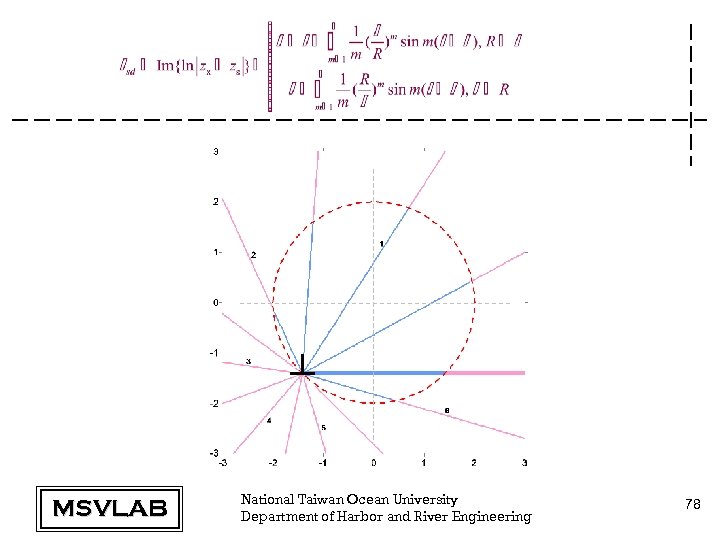
MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 78

An infinite medium containing one hole under the screw dislocation MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 79

Coated inclusion under the antiplane shear stress MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 80
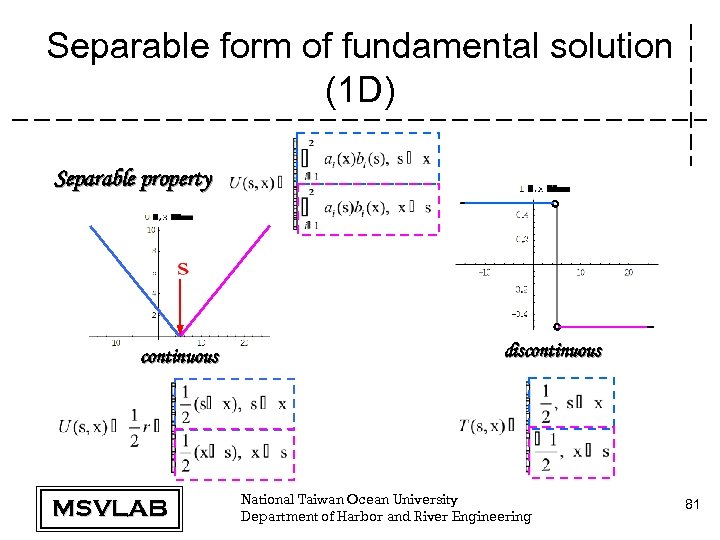
Separable form of fundamental solution (1 D) Separable property continuous MSVLAB discontinuous National Taiwan Ocean University Department of Harbor and River Engineering 81
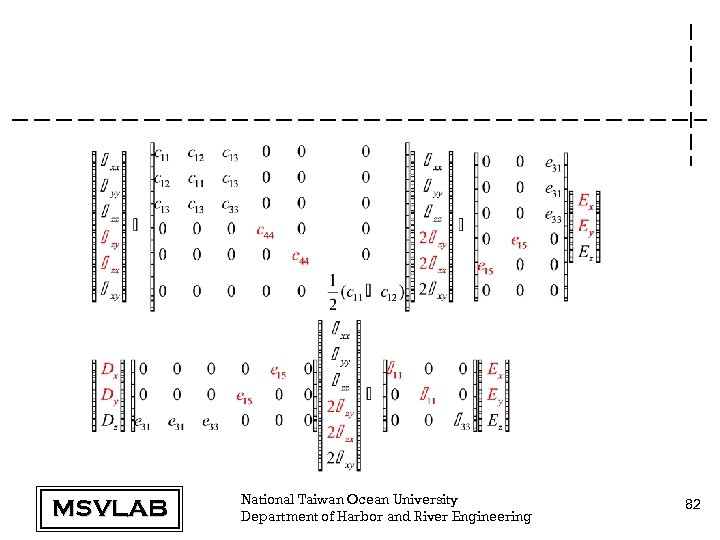
MSVLAB National Taiwan Ocean University Department of Harbor and River Engineering 82
a8c363a60eec2fb0769a28ca3d67657e.ppt