Nuclear Polarization Recent Results and Yet Another Discussion

Nuclear Polarization, Recent Results and Yet Another Discussion New Applications of HD S. Goertz Physics Institute, University Bonn

Contents: Part I: Physics basics of the polarized solid target • Luminosities of experiments with polarized targets • The quality factor of a polarized target: The Figure of Merit • The polarized target: Concept and components • The DNP process - The Solid State Effect (SSE) - The idea of Equal Spin Temperatures (EST) - The role of the electron spin resonance line - The problem of polarizing deuterons Part II: Material developments • Three examples for an optimized target material preparation

Part III: HD, brute force and beyond ? • Why HD ? Properties of H 2, D 2 and HD • Static polarization of HD • The relaxation switch • Polarization values calculated & measured • Pro‘s and Con‘s of statically polarized HD • The DNP option Summary

Part I: Physics basics of the polarized solid target

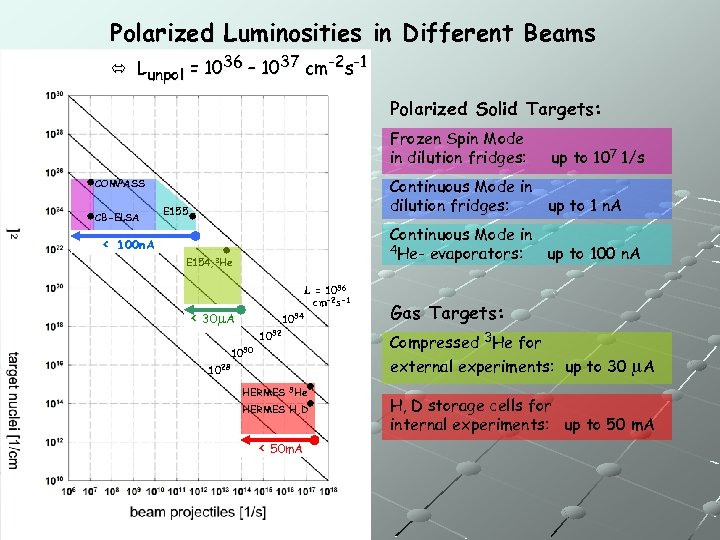Polarized Luminosities in Different Beams Lunpol = 1036 – 1037 cm-2 s-1 Polarized Solid Targets: Frozen Spin Mode in dilution fridges: Continuous Mode in dilution fridges: up to 1 n. A COMPASS CB-ELSA < up to 107 1/s E 155 Continuous Mode in 4 He- evaporators: up to 100 n. A 100 n. A E 154, 3 He L = 1036 cm-2 s-1 < 30 m. A 1034 1032 1030 1028 HERMES 3 He HERMES H, D < 50 m. A Gas Targets: Compressed 3 He for external experiments: up to 30 m. A H, D storage cells for internal experiments: up to 50 m. A

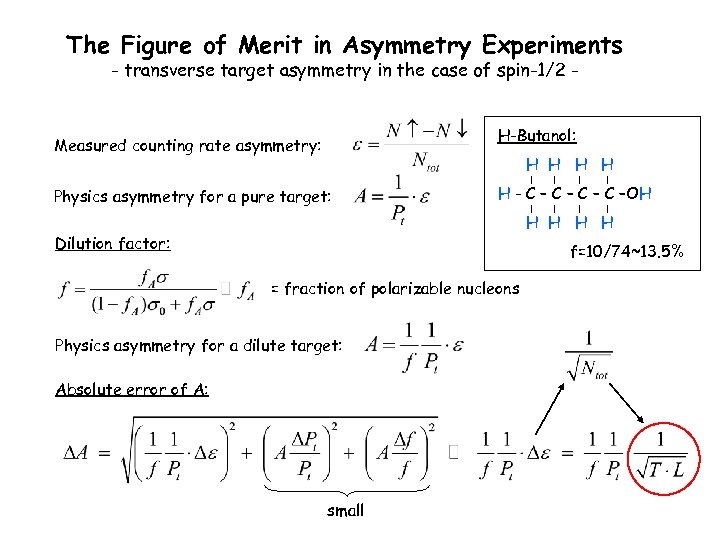The Figure of Merit in Asymmetry Experiments - transverse target asymmetry in the case of spin-1/2 H-Butanol: Measured counting rate asymmetry: H H Physics asymmetry for a pure target: H - C – C –OH H H Dilution factor: f=10/74~13. 5% = fraction of polarizable nucleons Physics asymmetry for a dilute target: Absolute error of A: small

Measuring time for DA = const : Target Figure of Merit: Typical Fo. M‘s (continuous polarization at B = 2. 5 T, COMPASS like dilution fridge) increasing radiation hardness Material r[g/cm 3] k (pack. f. ) f. A 2·Pt 2·r· 90 0. 985 0. 62 1 90 0. 853 0. 58 1. 37 0. 80 0. 55 1. 32 f. A[%] P[%] H-Butanol 13. 5 14 NH 17. 6 3 7 Li. H 1/8+0. 59/8 90 + 70 (? ) k D-Butanol 23. 8 45 / 90 (!) 1. 12 0. 62 1/4 14 ND 30 30 - 40 1. 00 0. 58 0. 6 – 1. 05 50 55 0. 82 0. 55 4. 3 3 6 Li. D

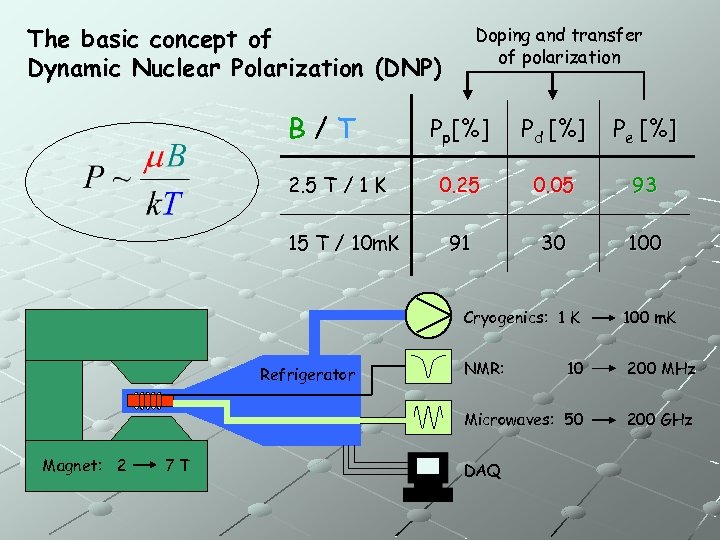The basic concept of Dynamic Nuclear Polarization (DNP) B/T 2. 5 T / 1 K 15 T / 10 m. K Doping and transfer of polarization Pp[%] Pd [%] Pe [%] 0. 25 0. 05 93 91 30 100 Cryogenics: 1 K Magnet: 2 7 T NMR: 10 200 MHz Microwaves: 50 Refrigerator 100 m. K 200 GHz DAQ

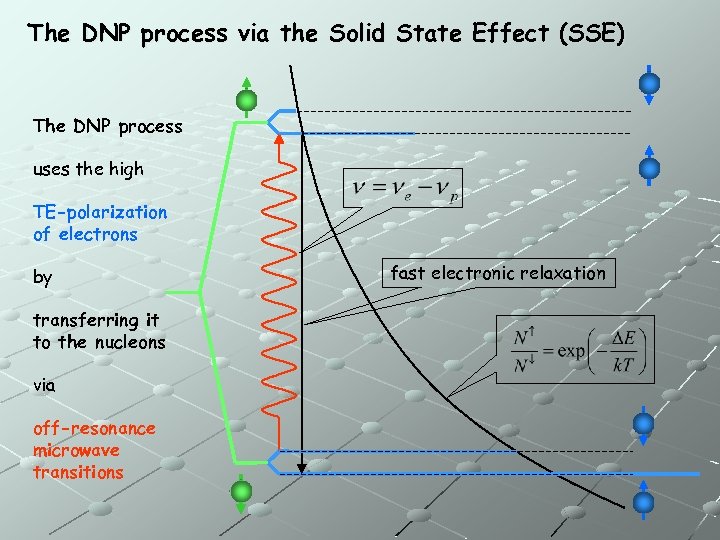The DNP process via the Solid State Effect (SSE) The DNP process uses the high TE-polarization of electrons by transferring it to the nucleons via off-resonance microwave transitions fast electronic relaxation

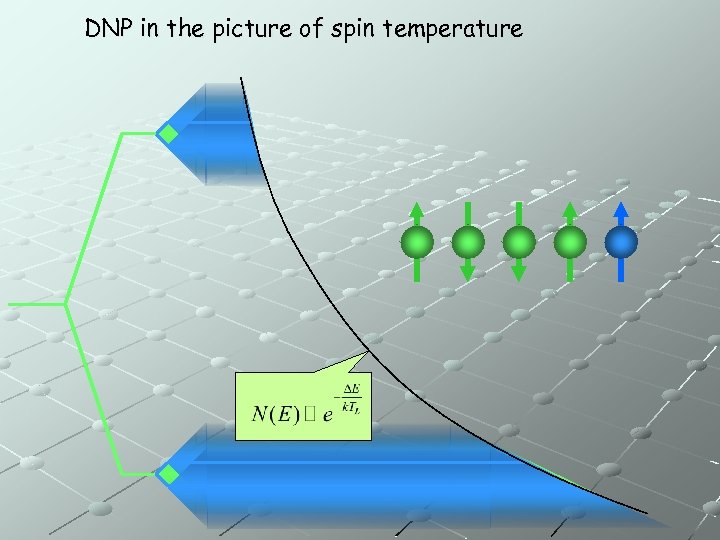DNP in the picture of spin temperature

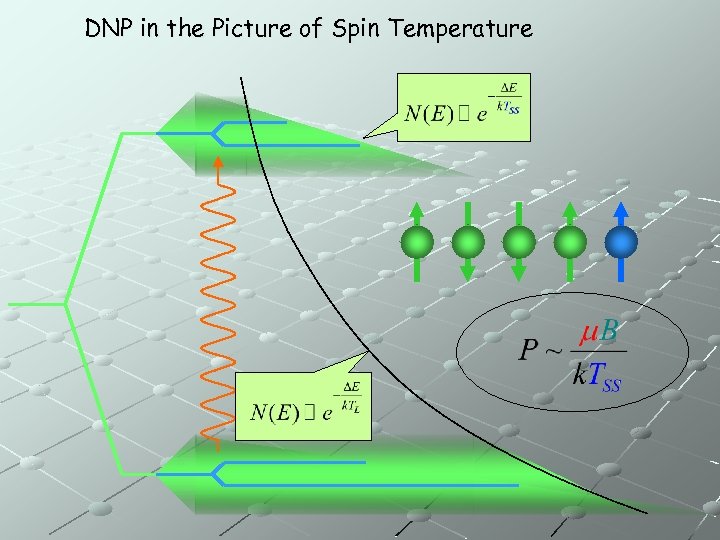DNP in the Picture of Spin Temperature

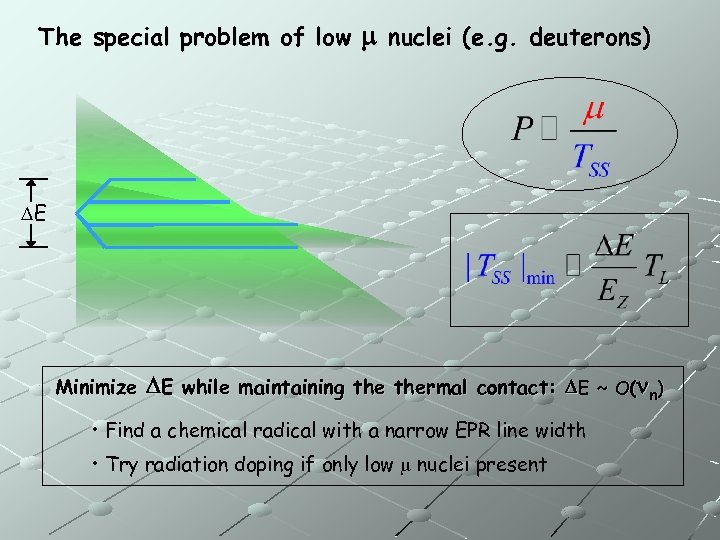The special problem of low m nuclei (e. g. deuterons) DE Minimize DE while maintaining thermal contact: DE ~ O(nn) • Find a chemical radical with a narrow EPR line width • Try radiation doping if only low m nuclei present

Part II: Material developments

Example 1: Electron irradiated 6 Li. D • Idea: A. Abragam 1980, Pioneer work at Saclay during 80‘s - 90‘s • Refinement of preparation: Since 1991 in Bonn, from 1995 in Bochum COMPASS D F-Center: • s-wave electron 20 Me. V at • no g-anisotropy T = 185 K HF interaction • weak 7 Li (larger + DE Li B m) impurity broadenes the EPR line lowers Pmax 1 liter for COMPASS: (2000 Bochum) Synthesized from highly enriched 6 Li. D Pmax = 55 % at 2. 5 T

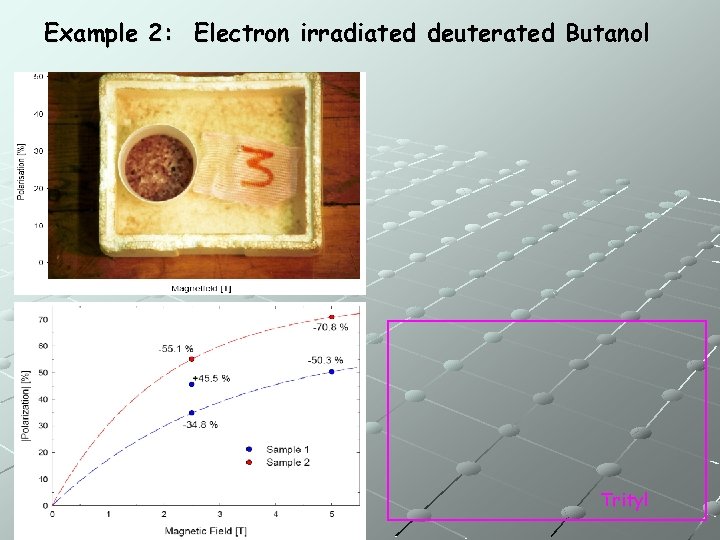Example 2: Electron irradiated deuterated Butanol Trityl

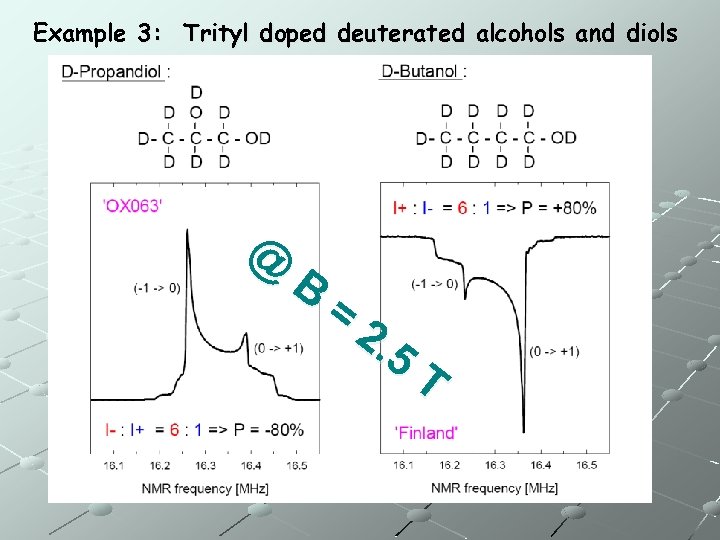Example 3: Trityl doped deuterated alcohols and diols @ B = 2. 5 T

Part III: HD, brute force and beyond ?

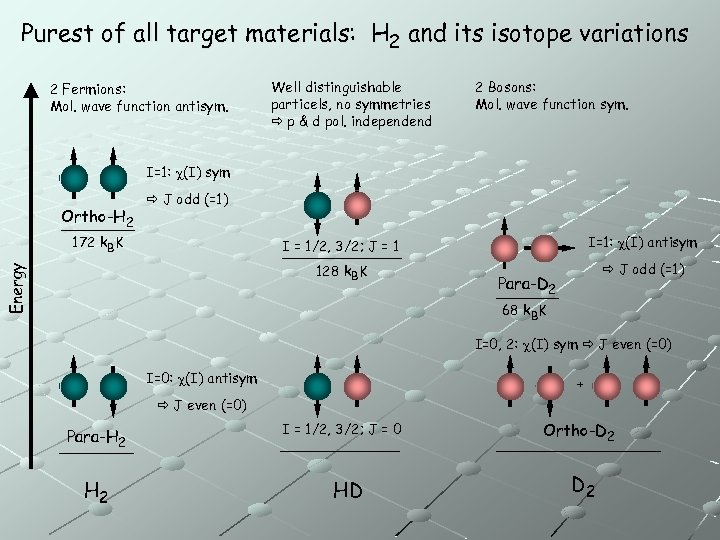Purest of all target materials: H 2 and its isotope variations 2 Fermions: Mol. wave function antisym. Well distinguishable particels, no symmetries p & d pol. independend 2 Bosons: Mol. wave function sym. I=1: c(I) sym Ortho-H 2 J odd (=1) I = 1/2, 3/2; J = 1 I=1: c(I) antisym 128 k. BK Energy 172 k. BK J odd (=1) Para-D 2 68 k. BK I=0, 2: c(I) sym J even (=0) I=0: c(I) antisym + J even (=0) Para-H 2 I = 1/2, 3/2; J = 0 HD Ortho-D 2

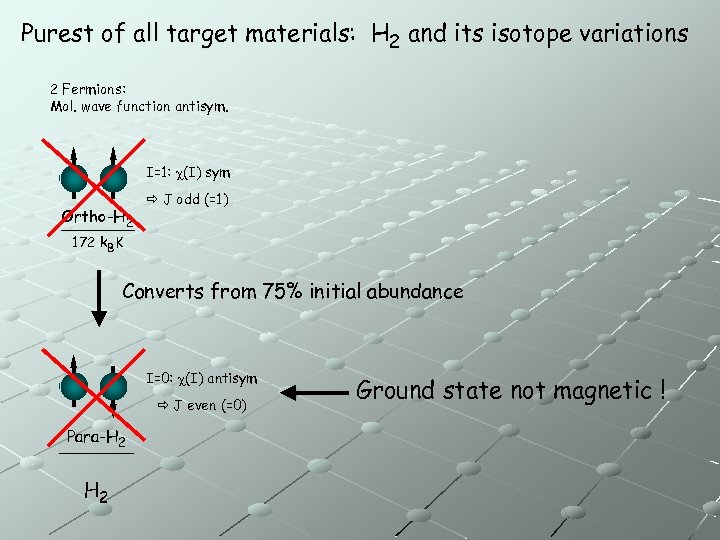Purest of all target materials: H 2 and its isotope variations 2 Fermions: Mol. wave function antisym. I=1: c(I) sym Ortho-H 2 J odd (=1) 172 k. BK Converts from 75% initial abundance I=0: c(I) antisym J even (=0) Para-H 2 Ground state not magnetic !

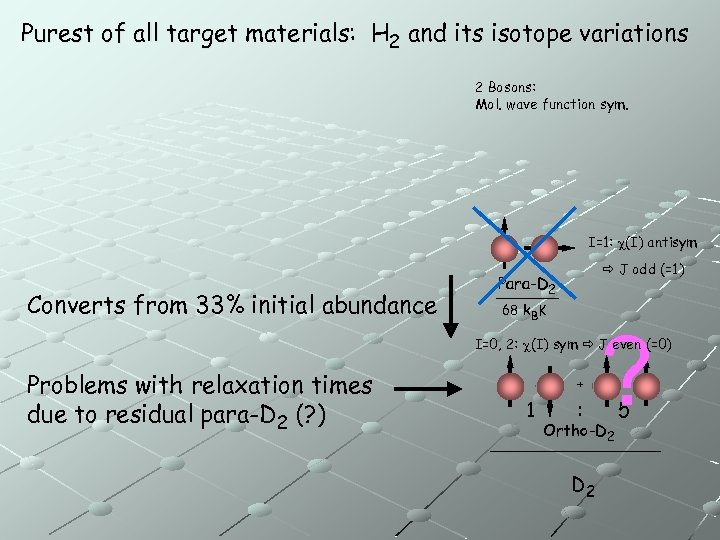Purest of all target materials: H 2 and its isotope variations 2 Bosons: Mol. wave function sym. I=1: c(I) antisym Converts from 33% initial abundance J odd (=1) Para-D 2 68 k. BK ? I=0, 2: c(I) sym J even (=0) Problems with relaxation times due to residual para-D 2 (? ) + 1 : Ortho-D 2 5

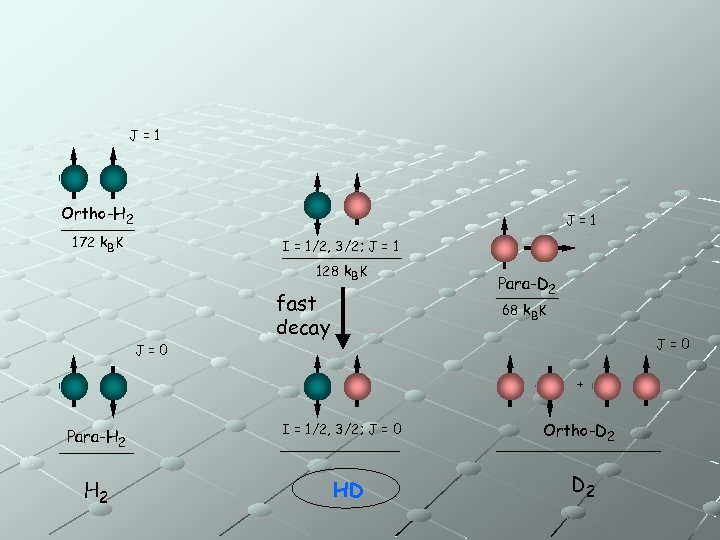J=1 Ortho-H 2 J=1 172 k. BK I = 1/2, 3/2; J = 1 128 k. BK fast decay Para-D 2 68 k. BK J=0 + Para-H 2 I = 1/2, 3/2; J = 0 HD Ortho-D 2

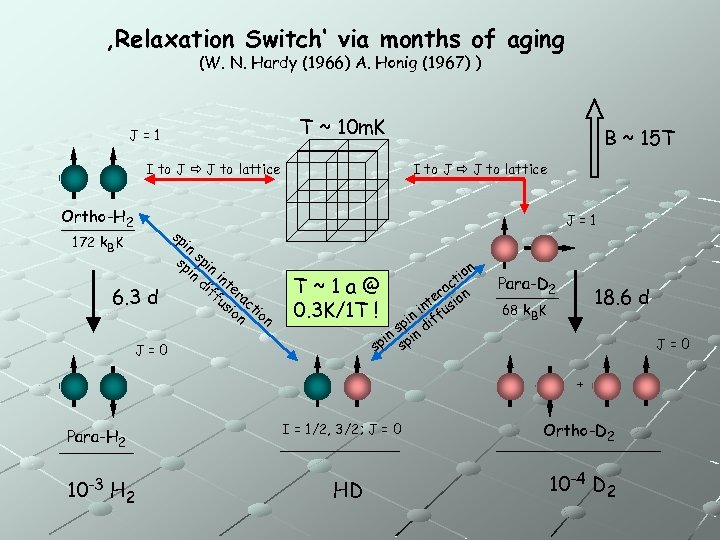‚Relaxation Switch‘ via months of aging (W. N. Hardy (1966) A. Honig (1967) ) T ~ 10 m. K J=1 I to J J to lattice Ortho-H 2 B ~ 15 T I to J J to lattice J=1 sp i 172 k. BK 6. 3 d J=0 n sp spin in in di te ff r us ac io tio n n n tio T~1 a@ ac er ion t in fus 0. 3 K/1 T ! in f sp n di in i sp sp Para-D 2 18. 6 d 68 k. BK J=0 + Para-H 2 10 -3 H 2 I = 1/2, 3/2; J = 0 HD Ortho-D 2 10 -4 D 2

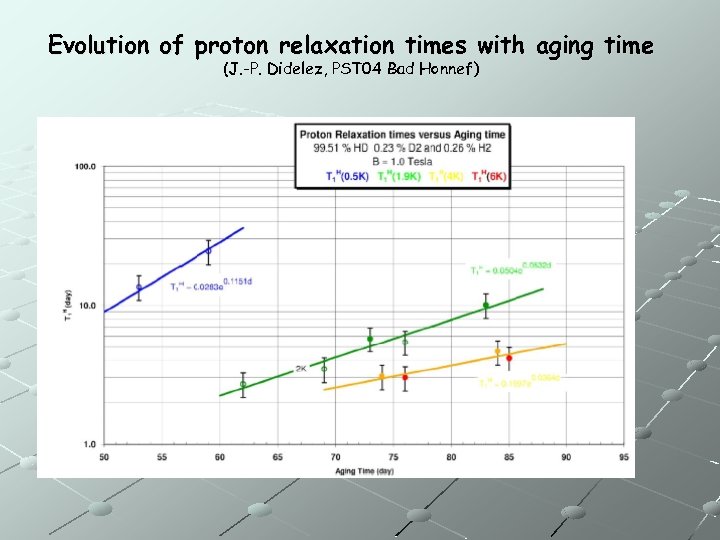Evolution of proton relaxation times with aging time (J. -P. Didelez, PST 04 Bad Honnef)

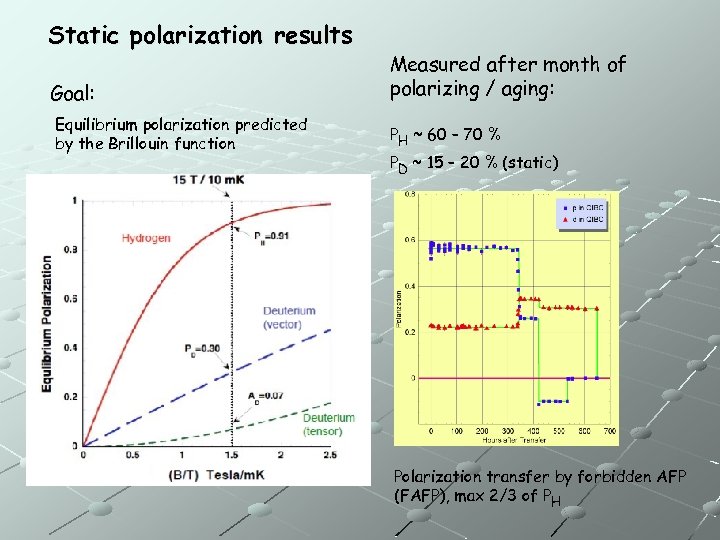Static polarization results Goal: Equilibrium polarization predicted by the Brillouin function Measured after month of polarizing / aging: PH ~ 60 – 70 % PD ~ 15 – 20 % (static) Polarization transfer by forbidden AFP (FAFP), max 2/3 of PH

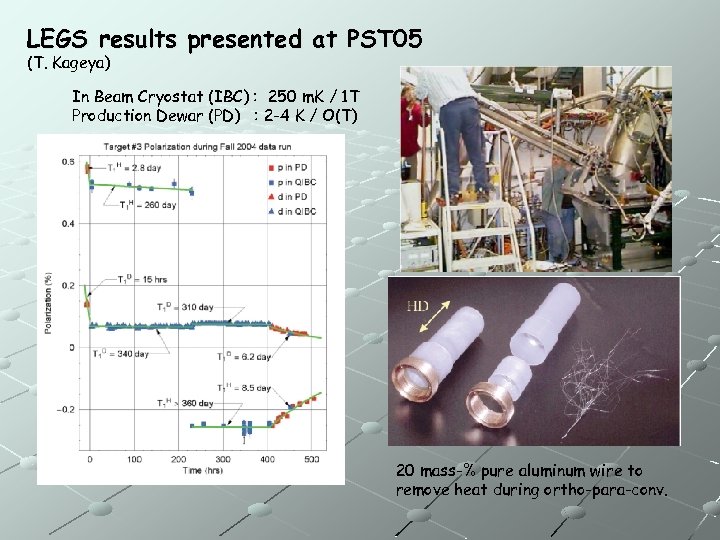LEGS results presented at PST 05 (T. Kageya) In Beam Cryostat (IBC) : 250 m. K / 1 T Production Dewar (PD) : 2 -4 K / O(T) 20 mass-% pure aluminum wire to remove heat during ortho-para-conv.

Advantages of HD as target material: Very low density (~ 0. 13 g/cm 3): Much less radiative background compared to other mat. Reduces luminosity and thus the Fo. M Target nuclei are only H and D: H and D may be polarized independently Almost no dilution (20 % aluminum + target cont. ) High value of the Fo. M: • Fo. M(HD, 70%/20%) ~ 2 · Fo. M(H-but, 90%) • Fo. M is highly dependent on the degree of polarization !

Drawbacks of the static method Very long production process, at least 3 - 4 months Very sophisticated handling: At least 4 cryostats needed: PD, TC, DR, IBC Production and NMR calibration in the PD Transfer to the dilution refrigerator: T(sample) = ? Transfer back to the PD for NMR measurement Transfer to the IBC for physics measurement Transfer back to the PD for final NMR meas. Accidents during the processes: Cryostat blockages, Power cuts, … Reliability of the NMR measurements: Long term stability ?

Radiation Resistance: Ok for real photons, shown in experiments in the past Unclear for charged particles of n. A currents Mano & Honig (1975): 10 Ge. V e-beam at T = 4. 2 K / B = 0. 28 T T 1 H decreased from 30000 s to 930 s after 8. 5 · 1012 e/cm 2 = 280 s at 5 n. A Radtke et al. (2005, Bochum): 2. 3 Me. V(max) b-radiation from 90 Sr source at T = 1 K / B = 2. 5 T: No degration of T 1 H until several 1014 e/cm 2 = sev. hours at 5 n. A Dedicated measurements needed !

Dynamic Polarization: Situation unclear either First attempts bei J. C. Solem (1973) - T = 4. 2 K and 1. 2 K, B = 0. 83 T and 1. 24 T - Creation of paramagnetic impurities (atomic H) by irradiation (60 Me. V Bremsstrahlung) - Admixture of 3 · 10 -4 O 2 to lower T 1 e - Best result: PH = 3. 75 % at 1. 2 K / 1. 24 T ~ 105 MHz In situ EPR at 1. 2 K O 2 D Pol. enhancement at 1. 24 T / 1. 3 K „Pure Solid Effect“ 50. 4 m. T

These results are very promising having in mind • the relatively high temperature of 1. 2 K • the low magnetic field of 1. 24 T One should be able to do a better job nowadays ! But: Unclear weather a real DNP-HD target is feasible at all ! Problems: 1) ‚In situ irradiation‘ must be possible at the experimental site or cold tranfer from the irradiation facility to the experiment ! 2) What happens with the D-polarization during / after DNP • Spin temperature equilibrium between H and D ? If no: How to polarize 2/3 of the material ? (SSE ? ) If yes: Same relation as in the static case • Cross relaxation when paramagnetic impurities present ? If yes: Independent polarization of H and D lost !

3) DNP via SSE requires high microwave power levels ! These are acceptable only by evaporation cryostats ! on the other hand: Paramagnetic centers require conventional frozen spin techniques to maintain the polarization in combination with 4 p-detectors ! Possible solutions to 3): 1) Further development of internal (thin) polarization coils (!) Under investigation in Bonn since years (challenging !) 2) Detector ‚inside‘ the polarizing magnet (!) Planned for the Crystal Barrel detector at Bonn (1) or (2) allows continuous mode while maintaining a 4 p geometry 3) Paramagnetic impurities of a different nature (? ) Polarization via spin temperature equilibrium 4) Combined 4 He evaporation + 3 He/4 He dilution refrigerator (? ) Probably impossible in the usual horizontal configuration

Summary: In 1957 Abragam & Jeffries proposed the ‚Solid Effect‘ as a possible mechanism to produce enhanced nuclear spin polarization in a solid. After half a century of continuous research: 1. Not only the H, also the D can be polarized nearly completely ! 2. A polarized solid target can be adapted to nearly every experimental set-up ! Left: The dream of a pure AND highly polarized solid target This dream may be dreamed in form of dynamically polarized HD But it‘s still unclear whether: 1. a high dynamic polarization of H and D in HD is technically possible 2. such a target really competes with / wins over conventional designs

The bare necesseties: • New and strong efforts needed to clarify these questions ! • Not possible for one ‚curious professor‘ and his Ph. D student • Experienced working group needed dedicated only to this research field But it may be the last big adventure in polarized target material research !