Nuclear Physics Lectures 1 Cross Sections •

Nuclear Physics Lectures 1 Cross Sections • Definition of Cross Section – Why its useful. • Breit-Wigner Resonances • Rutherford Scattering

Nuclear Physics Lectures 2 Cross-Sections • Why concept is important – Learn about dynamics of interaction and/or constituents (cf Feynman’s watches). – Needed for practical calculations. • Experimental Definition • How to calculate – Fermi Golden Rule – Breit-Wigner Resonances – QM calculation of Rutherford Scattering

Nuclear Physics Lectures 3 Definition of • a+b x • Effective area for reaction to occur is Beam a dx. N a (0) particles type a/unit time hit target b N b atoms b/unit volume Number /unit area= N b dx Probability interaction = N b dx d. N a =-N a N b dx N a (x)=N a (0) exp(-x/ ) ; =1/(N b )

Nuclear Physics Lectures 4 Reaction Rates • Na beam particles/unit volume, speed v • Flux F= N a v • Rate/target b atom R=F • Thin target x<< : R=(N b T ) F Total • This is total cross section. Can also define differential cross sections, as a function of reaction product, energy, transverse momentum, angle etc. • d. R(a+b c+d)/d. E=(N b. T ) F d (a+b c+d) /d.

Nuclear Physics Lectures 5 Breit-Wigner Line Shape • Start with NR Schrödinger equation: nn 0 n n )/ti. Eexp()t(a)t(; H dti n m mmnnnnnnn )/ti. Eexp(Ha)/ti. Eexp(Ea)/ti. Eexp(ai X by n and integrate rd. HHrdnmmnnmnm 3*3* ; m mmnmnnnnnti. EHati. EEati. Eai)/exp()/exp( Start in state m exponential decay )2/texp()t(a m )/texp()t(a 2 m

Nuclear Physics Lectures 6 Breit-Wigner Line Shape — 2 }/t]2/)EE(iexp{[Hai mnmnn /t]2/)EE(iexp[Hdt)t(aimnmn t 0 mn mnmn n 2/)EE(i /t]2/)EE(iexp[H )t(a For 2/)EE(i H )t(a mn mn n /t

Nuclear Physics Lectures 7 Breit-Wigner Line Shape -3 )EE(PH 2 )t(a 4/)EE( H )t(a nm 2 mn 2 n 22 nm 2 mn 2 n 4)EE( 1 2)EE(P 22 nm nm Normalised Breit-Wigner line shape Q: where have you seen this shape before? We will see this many times in NP and PP.

Nuclear Physics Lectures 8 Breit-Wigner Resonance • Important in atomic, nuclear and particle physics. • Uncertainty relationship • Determine lifetimes of states from width. =FWHM; ~t. E /~

Nuclear Physics Lectures 9 Fermi Golden Rule • Want to be able to calculate reaction rates in terms of matrix elements of H. • Warning: We will use this many times to calculate but derivation not required for exams, given here for completeness.

Nuclear Physics Lectures 10 Discrete Continuum • Decays to a channel i (range of states n). Density of states ni (E). Assume narrow resonance d. E)EE(P)E(n. H 2 P 0 i 2 0 ii Totalii. Totali i RPR; R; P )E(n. H 2 R 0 i 2 0 ii i

Nuclear Physics Lectures 11 Cross Section • Breit Wigner cross section. • Definition of and flux F: )r. kiexp(V 2/1 FR v. VF 1 2 3 k 4 )2( V )k(n v dk d. E ; m 2 )k( E 2 v k 4 )2( V )E(n

Nuclear Physics Lectures 12 Breit-Wigner Cross Section • Combine rate, flux & density states 4/)EE( E 2 1 k 4 V v)2( v. V 22 01 f 1 i 23 f 22 01 f 2 o 4/)EE( H )t(a. R )E(n. H 2)E( 2 10 i 4/)EE( E )E(n 1 2 1 R 22 01 f 1 i

Nuclear Physics Lectures 13 Breit-Wigner Cross Section 4/)EE(k 22 01 fi 2 n + 16 O 17 O

Nuclear Physics Lectures 14 Low Energy Resonances • n + Cd total cross section. • Cross section scales ~ 1/E 1/2 at low E. • B-W: 1/k 2 and ~n(E)~k

Nuclear Physics Lectures 15 Rutherford Scattering 11 c; c 4 e ; r ZZ )r(V 02 21 )r. kiexp(V; )r. kiexp(Vf 2/1 fi 2/1 i rd)r. kiexp( r ZZ )r. kiexp(VH 3 f 21 i 1 fi kkq rd r )r. qiexp( ZZVH 3 211 fi cosddrr r )cosiqrexp( 2 ZZVH 2 211 fi

Nuclear Physics Lectures 16 Rutherford Scattering 2 drr iqr )iqrexp( 2 ZZVH 2 221 1 fi a)a/rexp(); r(x. V drriqa iq. ZZ VH fi )/1 exp(2 211 iqa/1 1 iq 2 ZZ VH 211 fi

Nuclear Physics Lectures 17 Rutherford Scattering 3 • Fermi Golden Rule: f 2 fi d. E dn H 2 R v/1 d. E dp ; d. E dp dp dn d. E dn ; 4 d h V p 4 dp dn 3 2 )22(; )2( )( 32 hd v Vp En v. VF; F/R 1 v V )2(v Vp Vq 4 ZZ 2 d d 322 221 42 2 21 2 )(4 qv ZZp d d

Nuclear Physics Lectures 18 Rutherford Scattering 4 )2/(sinp 4)cos 1(p 2)pp(q 2222 fi 2 )2/(sin 4 )( 422 2 21 vp ZZ d d Compare with experimental data at low energy Q: what changes at high energy ? p i p f

Nuclear Physics Lectures 19 Low Energy Experiment • Scattering of on Au & Ag agree with calculation assuming point nucleus Sin 4 ( /2)d N /d c o s

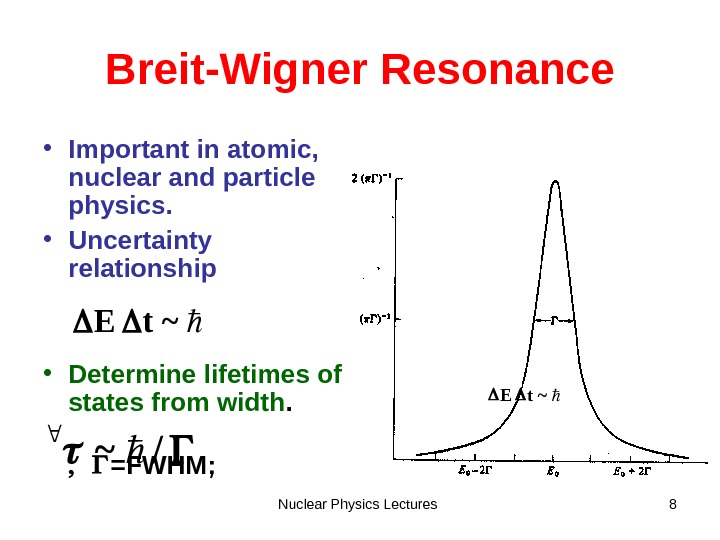
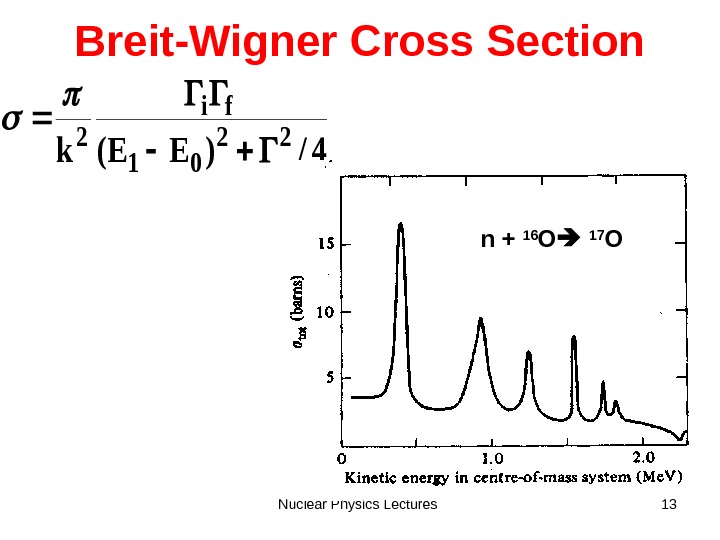
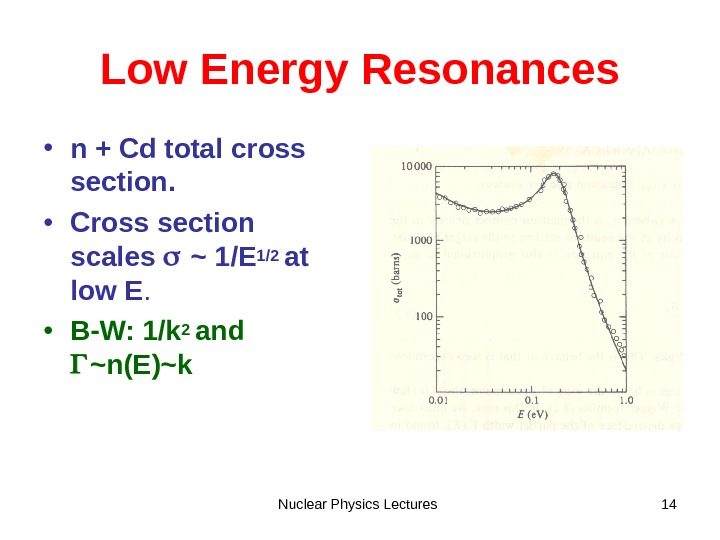
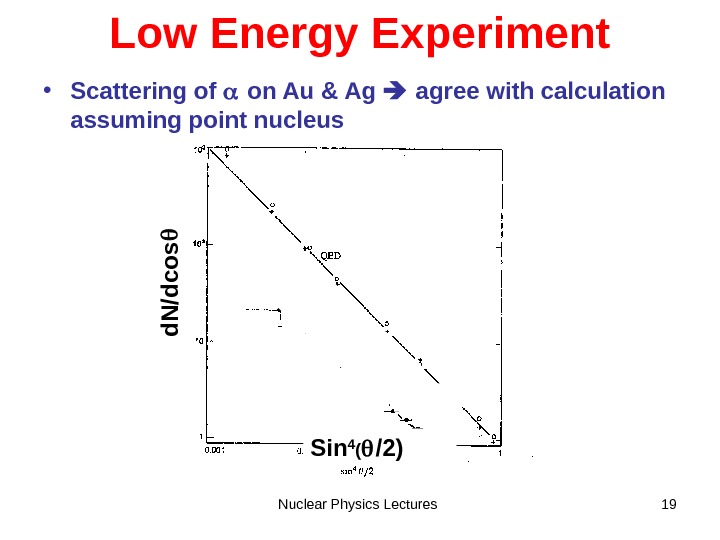
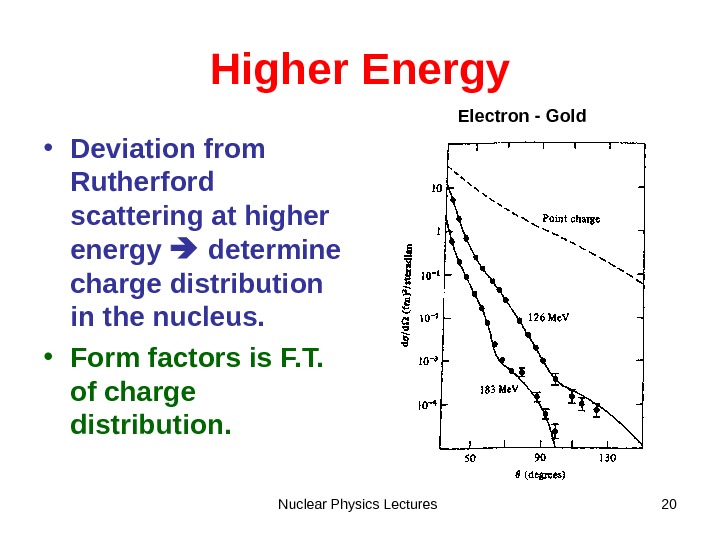
Nuclear Physics Lectures 20 Higher Energy • Deviation from Rutherford scattering at higher energy determine charge distribution in the nucleus. • Form factors is F. T. of charge distribution. Electron — Gold