нства ак раве призн Первый еугольников тр

нства ак раве призн Первый еугольников тр

E Теоретический опрос • Какая фигура называется треугольником? • Какие треугольники называются равными? • Назовите углы ∆ DEK, прилежащие к стороне EK, DE, DK. D K S • Назовите угол ∆ DEK, заключенный между сторонами DE и DK, EK и DE. • Между какими сторонами ∆ DEK заключен угол К? P M • ∆ DEK = ∆ PSM. Назовите равные стороны и равные углы в этих треугольниках. 2

Закончите предложения -Треугольники называются равными, если у них … -Два отрезка называются равными, если они … -Два угла называются равными, если они …

Какие условия должны выполняться для того, чтобы ∆ АВС был равен ∆ А 1 В 1 С 1? В А А 1 С В 1 АВ = А 1 В 1 АС = А 1 С 1 ВС = В 1 С 1 4

Вставь слово Фигуры называются ______, если при наложении их друг на друга соответствующие точки совпадут Два отрезка называются ______ , если при наложении друг на друга их концы совпадут. Фигура состоящая из трех точек не лежащих на одной прямой и трех отрезков попарно соединяющих эти точки называется _________ Точки называются______ А отрезки называются его______ В А Сумма сторон треугольника называется его _________ Между сторонами АВ и АС лежит угол А Утверждение, истинность которого требует доказательства называется______ Теорема состоит из _______ и _________ С

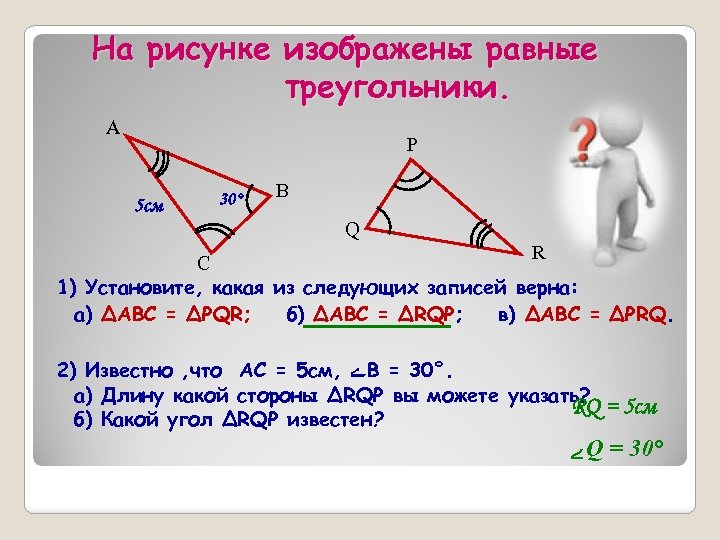На рисунке изображены равные треугольники. А P 5 см 30° В Q R С 1) Установите, какая из следующих записей верна: а) ∆ABC = ∆PQR; б) ∆ABC = ∆RQP; в) ∆ABC = ∆PRQ. 2) Известно , что АС = 5 см, ے В = 30°. а) Длину какой стороны ∆RQP вы можете указать? RQ = 5 см б) Какой угол ∆RQP известен? ے Q = 30°

Задача М В К Т С А Дано: ∆АВС = ∆МТК Найдите соответствующие равные элементы.

Дан Δ CDM. а) Назовите углы, прилежащие стороне CD. б) Назовите угол, лежащий против стороны СМ. в) Назовите углы, заключённые между сторонами СМ и MD, CD и DM.

Треугольник играет в геометрии особую роль. Без преувеличения можно сказать, что вся (или почти вся) геометрия со времён «Начал» Евклида покоится на «трёх китах» – признаках равенства треугольников.

В треугольнике выделяют шесть основных элементов – три внутренних угла и три соответственно противолежащие им стороны. Равенство треугольников устанавливается по равенству трех элементов: 1) двум сторонам и углу между ними; 2) по стороне и прилежащим к ней углам; 3) по трём сторонам.

Признак – показатель, примета, знак, по которым можно узнать, определить что–нибудь. Различительные признаки: признаки пола, признаки весны, признаки делимости и т. п. В геометрии некоторое условие, при которых два заданных треугольника оказываются равными, называется признаком равенства треугольников В математике каждое утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой, а сами рассуждения называются доказательством теоремы. Условие – это уже известные факты, о которых говориться в теореме, а заключение – это то, что нужно получить, доказать. 11

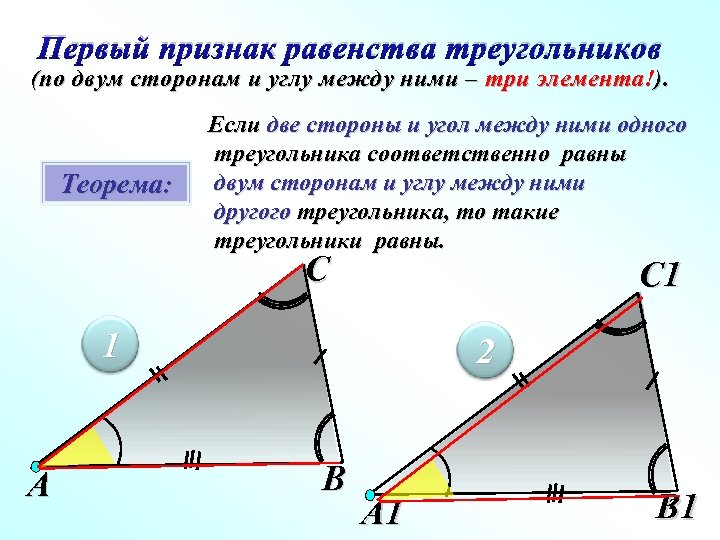Первый признак равенства треугольников (по двум сторонам и углу между ними – три элемента!). Теорема: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. С С 1 1 А 2 В А 1 В 1 12

Теорема: (условие) ∆АВC, ∆А₁В₁С ₁, АВ = А₁В₁, Дано: АС = А₁С₁, ∠А =∠А₁. Доказать: (заключение) ∆АВC = ∆А₁В₁С ₁, С 1 А С₁ 2 В А₁ Доказательство. В₁ Так как ∠А =∠А₁, то ∆АВC можно наложить на ∆А₁В₁С ₁ так, что вершина А совместится с вершиной А₁.

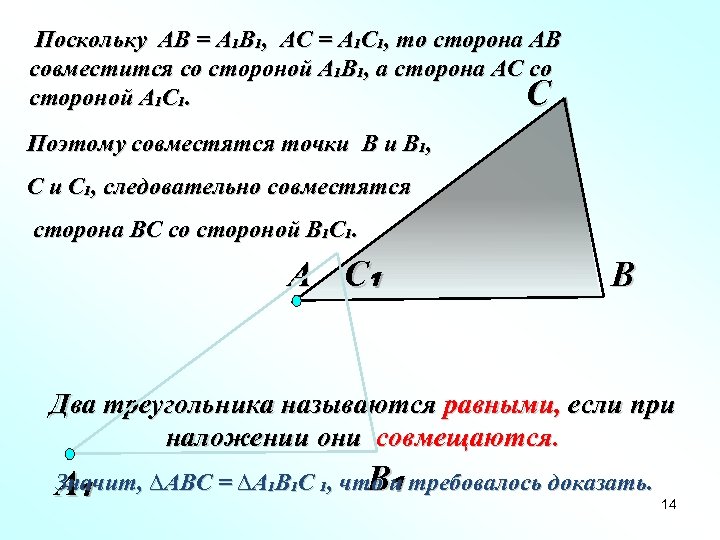Поскольку АВ = А₁В₁, АС = А₁С₁, то сторона АВ совместится со стороной А₁В₁, а сторона АС со С стороной А₁С₁. Поэтому совместятся точки В и В₁, С и С₁, следовательно совместятся сторона ВС со стороной В₁С₁. А С₁ В Два треугольника называются равными, если при наложении они совмещаются. Значит, ∆АВC = ∆А₁В₁С ₁, что и требовалось доказать. В₁ А₁ 14

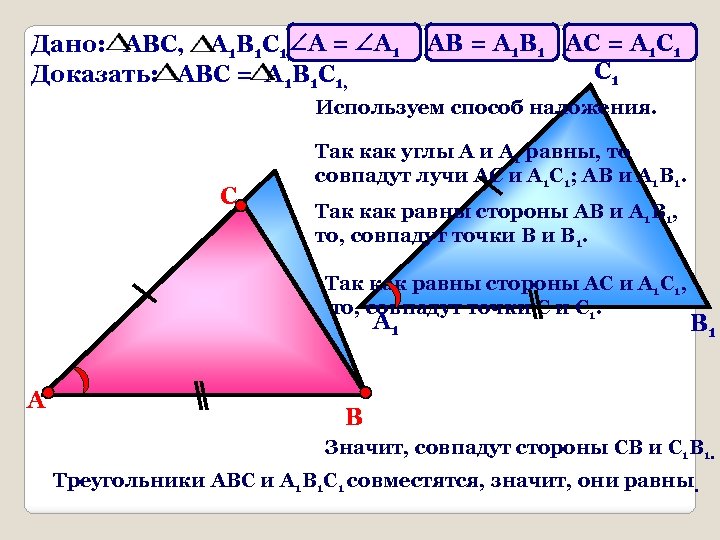Дано: АВС, А 1 В 1 С 1, А = А 1 Доказать: АВС = А 1 В 1 С 1, АВ = А 1 В 1 АС = А 1 С 1 Используем способ наложения. С Так как углы А и А 1 равны, то совпадут лучи АС и А 1 С 1; АВ и А 1 В 1. Так как равны стороны АВ и А 1 В 1, то, совпадут точки В 1. Так как равны стороны АС и А 1 С 1, то, совпадут точки С 1. А 1 А В 1 В Значит, совпадут стороны СВ и С 1 В 1. Треугольники АВС и А 1 В 1 С 1 совместятся, значит, они равны.

Какое условие должно еще выполняться, чтобы треугольники были равны? 2) 1) 3) 16

ПЛАН решения задач на доказательство равенства треугольников. = Чтобы доказать, что , нужно найти у них 3 пары соответственно равных элементов. С)___________; У)___________; С)____________. Значит, по = признаку равенства треугольников.

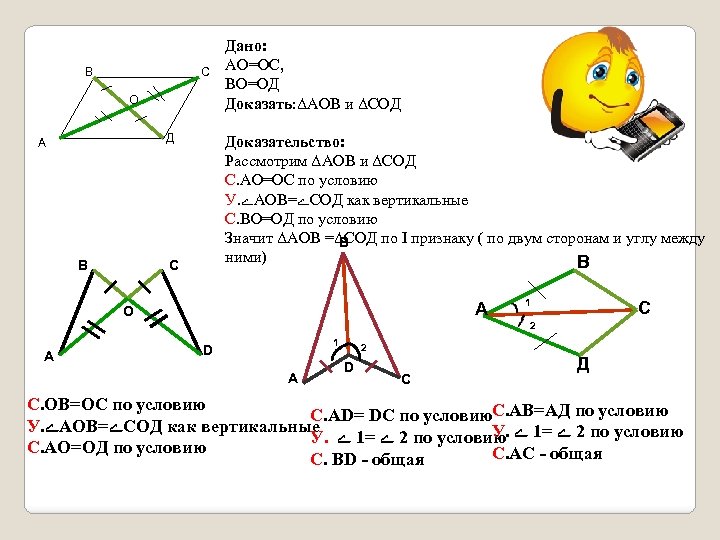В С О Д А В Дано: АО=ОС, ВО=ОД Доказать: ΔАОВ и ΔСОД Доказательство: Рассмотрим ΔАОВ и ΔСОД С. АО=ОС по условию У. ے АОВ= ے СОД как вертикальные С. ВО=ОД по условию Значит ΔАОВ =ΔСОД по I признаку ( по двум сторонам и углу между В ними) В С А О 1 С 2 А 1 D А 2 D C Д С. ОВ=ОС по условию С. АD= DC по условию. С. АВ=АД по условию У. ے АОВ= ے СОД как вертикальные У. У. 2 ے =1 ے по условию С. АО=ОД по условию С. АС - общая С. BD - общая

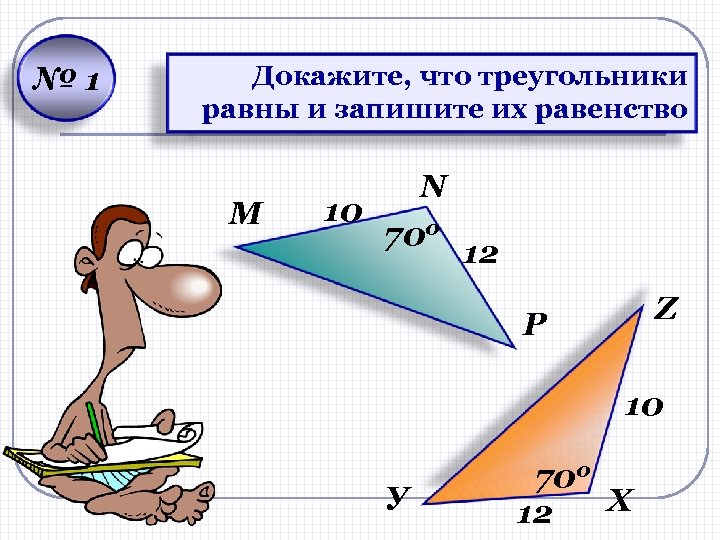№ 1 Докажите, что треугольники равны и запишите их равенство M N 10 700 12 Z P 10 У 700 Х 12

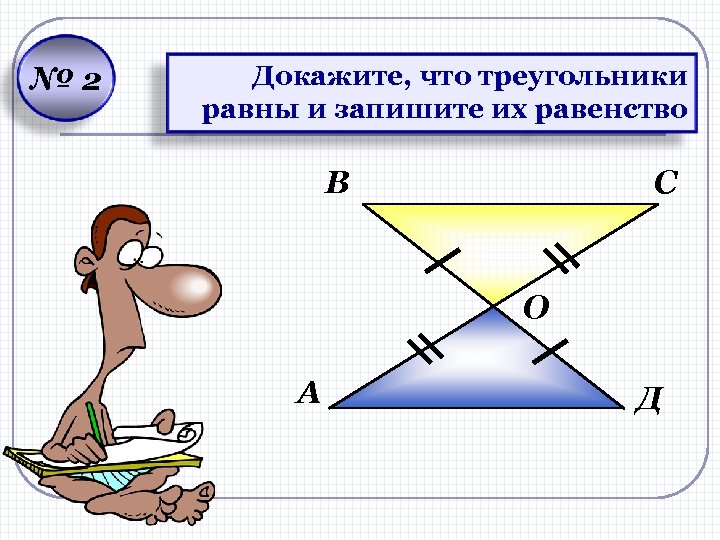№ 2 Докажите, что треугольники равны и запишите их равенство В С О А Д

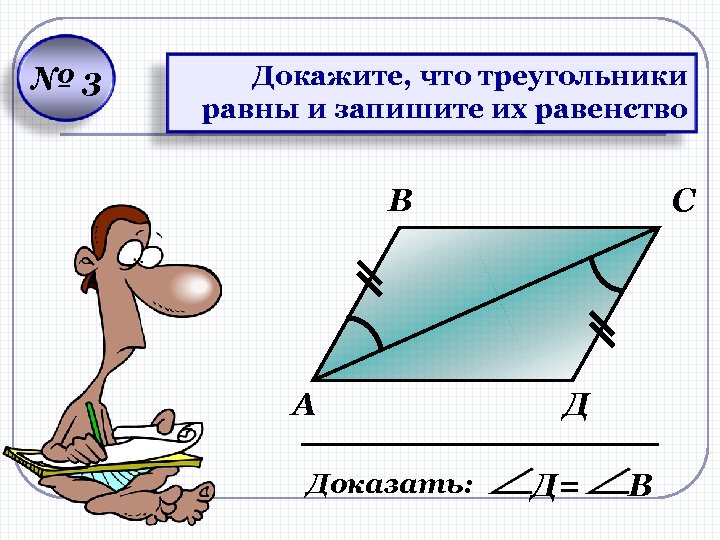№ 3 Докажите, что треугольники равны и запишите их равенство В А Доказать: С Д Д= В

№ 4 Докажите, что треугольники равны и запишите их равенство В 1 А 2 С Доказать: АВ=ВС Д

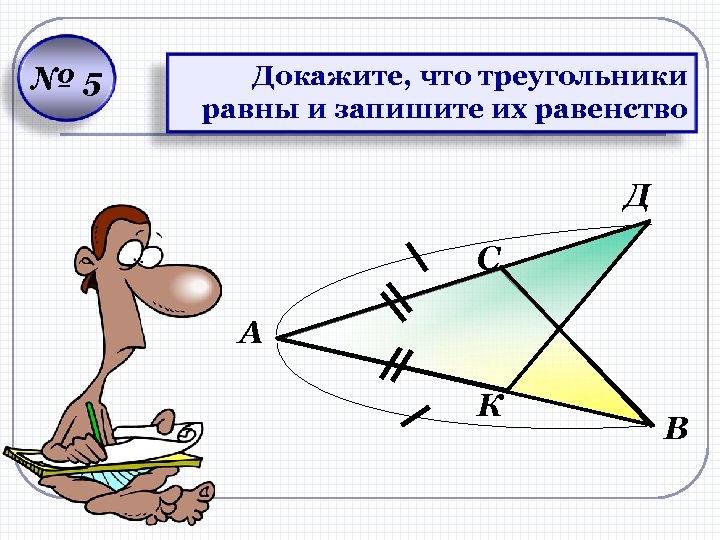№ 5 Докажите, что треугольники равны и запишите их равенство Д С А К В

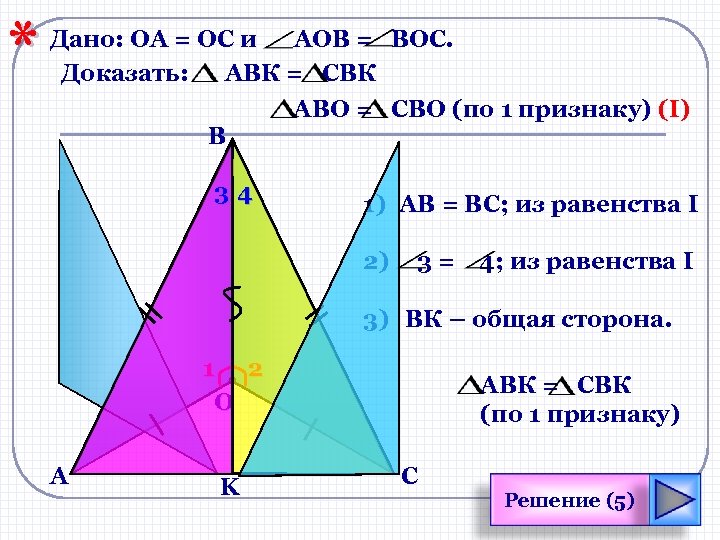* Дано: ОА = ОС и АОВ = ВОС. Доказать: АВК = CBК АВО = CBО (по 1 признаку) (I) B 34 1) АВ = ВС; из равенства I 2) 3= 4; из равенства I 3) ВК – общая сторона. 1 2 О А K АВК = CBК (по 1 признаку) С Решение (5)

Рефлексия урока Какие треугольники равны, Я сразу узнаю, Потому что 1 признак Верно применяю Элементы равные В треугольнике Я быстро распознаю, И тебе сейчас Про них напоминаю: Сторона, сторона И угол в одном, Сторона, сторона И угол в другом Угол между ними!! Помни про это Не забывай И задачи правильно решай

ЗАДАЧА № 1 С D F А В Доказать: CDF= АBF

ЗАДАЧА № 2 N M K Доказать: MNK= FNK F

ЗАДАЧА № 3 AD – биссектриса угла А; АВ = АС. Докажите: BD = CD. Решение. Δ ABD = Δ ACD по двум сторонам и углу между ними, т. к. у них AB = AC по условию, AD - общая, ے BAD = ے CAD, потому что AD биссектриса угла A. Из равенства треугольников следует равенство соответствующих сторон. Значит , BD = CD.

Сколько равных элементов треугольников необходимо найти и какие, чтобы сказать: «Треугольники равны по первому признаку равенства треугольников»

Информационные источники Литература. 1. Погорелов А. В. Геометрия: учебник для 7 – 9 кл. общеобразовательных учреждений/ А. В. Погорелов. М. : Просвещение, 2010. 2. Геометрия. 7 класс: поурочные планы по учебнику А. В. Погорелова/ авт. – сост. Е. П. Моисеева. - Волгоград: Учитель, 2006. 4. Геометрия. Рабочая тетрадь для 7 класса/Мищенко Т. М. – М. : Издательский Дом «Генжер» , 2000. 5. Тематический контроль по геометрии. 7 -9 класс/Мищенко Т. М. – М. : Издательский Дом «Генжер» , 1997. 7. Энциклопедический словарь юного математика/Сост. А. П. Савин. – М. : Педагогика, 1989. Интернет – ресурсы. 1. http: //images. yandex. ru 2. http: //www. montgomeryschoolsmd. org/sschools/rockvillehs/images/ MCButtons/ teacher. jpg 3. http: //www. profistart. ru/ps/blog/24031. html 4. http: // festival. 1 september. ru/articles/104251/