NP-полнота и сложность Задачи Штейнера Нечаева Инна 7381

NP-полнота и сложность Задачи Штейнера Нечаева Инна 7381

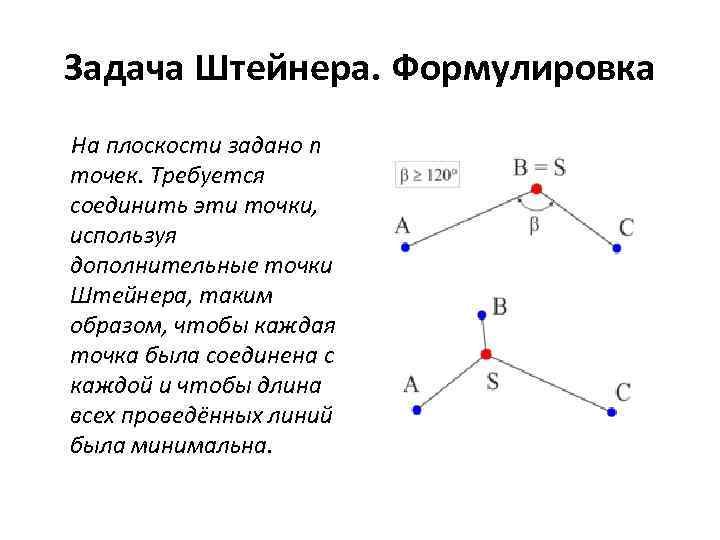Задача Штейнера. Формулировка На плоскости задано n точек. Требуется соединить эти точки, используя дополнительные точки Штейнера, таким образом, чтобы каждая точка была соединена с каждой и чтобы длина всех проведённых линий была минимальна.

Достаточные условия • В решение могут входить промежуточные точки, и все соединения должны быть отрезками, соединяющими точки (исходные и промежуточные). • В каждой промежуточной точке должны сходиться три отрезка • В исходных точках должны сходиться не более трёх отрезков. • Угол между отрезками, сходящимися в одной точке не должен быть меньше 120 градусов

Типы задач Штейнера. • Евклидова задача Штейнера • Линейная задача Штейнера • Задача Штейнера на графах.

Гипотеза Гильберта-Поллака Пусть на плоскости задано произвольное множество из n точек. Обозначим LМ длину минимального остовного дерева, которое стягивает эти точки, и LS – длину минимального дерева Штейнера. Для любого конечного множества точек на плоскости

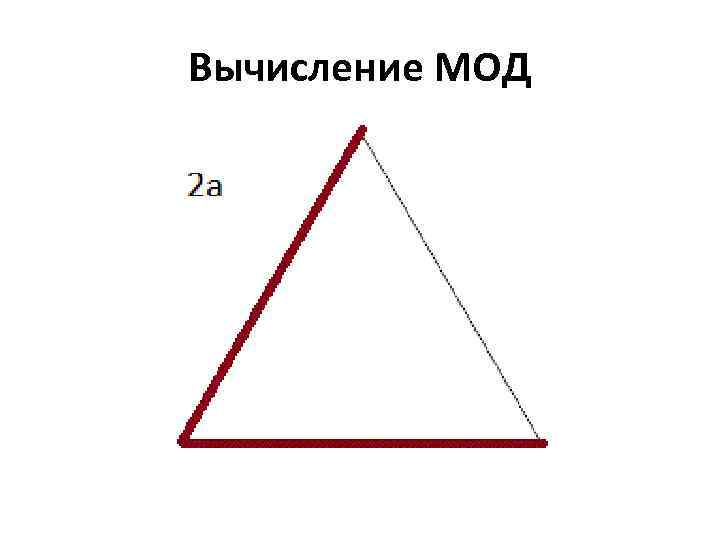Вычисление МОД

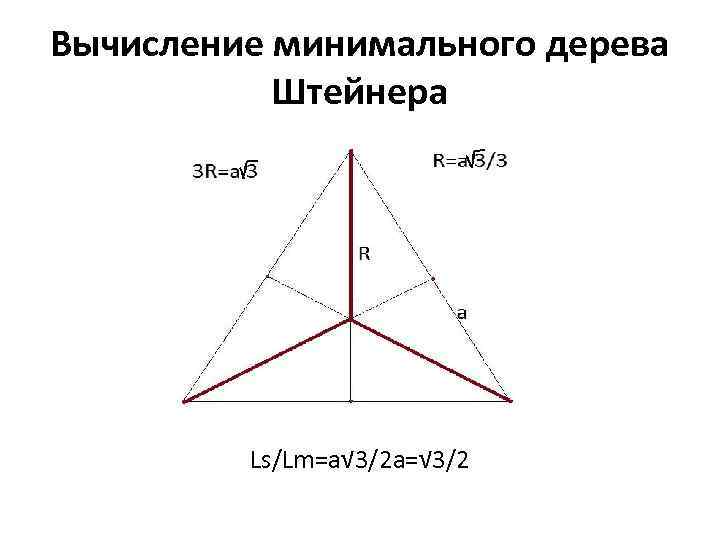Вычисление минимального дерева Штейнера Ls/Lm=a√ 3/2 a=√ 3/2

Вычисление МОД

Вычисление минимального дерева Штейнера Ls/Lm=14/15=0. 93 0. 87<0. 93<1

NP-полные задачи

Задача Штайнера NP-полная Грэм, М. Гэри, Джонсон : Теорема: задача Штейнера на графах является NP-полной. Доказательство: 1. показать, что P принадлежит классу NP; 2. Выбрать известную NP-полную задачу из P`; 3. Построить преобразование f из P` в P; 4. доказать, что f-полиномиальное преобразования.

Пункт 1. Задача Штайнера принадлежит классу NP Предположим , например принадлежит классу NP. В этом случае, существует такое решение , и мы можем проверить за полиномиальное время, что: • T действительно дерево: оно не содержит циклов и оно связно; • дерева T касается всех терминалов указанного множества R; • число ребер, которые включает дерево не более k.

Пункт 2. Задача точного покрытия трёхэлементными множествами Дано: • конечного множества X с |X| = 3 q; • Множество C состоящее из 3 -элементных подмножеств Вопрос: Существует ли такое подсемейство С C`, которое соответствует и • члены решения C` образуют разбиение множества X; • .

Пункт 3. Преобразование из X 3 C в ST Приведём пример точного покрытия трёхэлементными множествами , которое определяется множеством и группой трёхэлементных множеств Необходимо построить ST такое, что множество терминалов графа G = (V, E) будет равно R и длина остовного дерева не будет превосходить k.

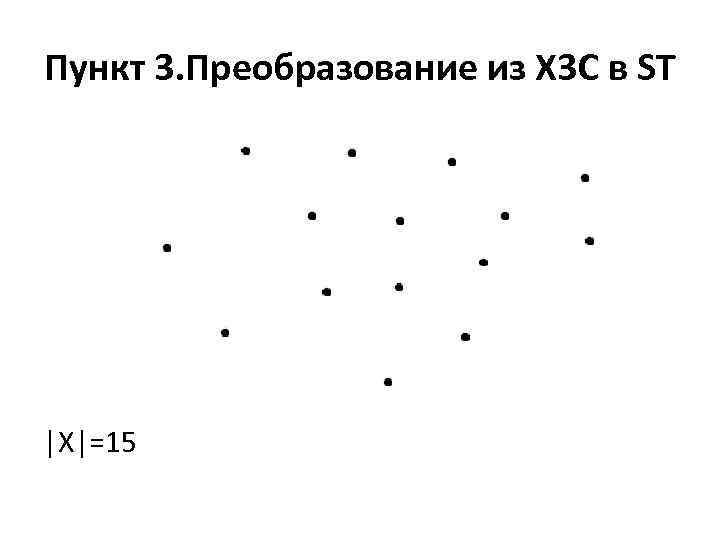Пункт 3. Преобразование из X 3 C в ST |X|=15

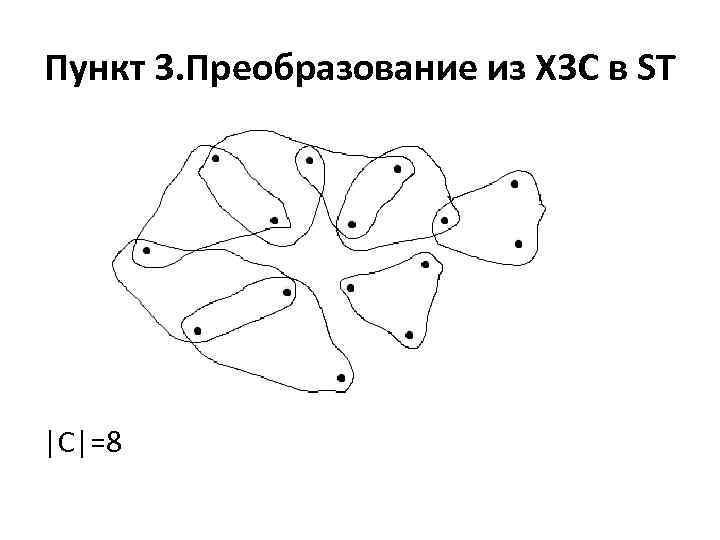Пункт 3. Преобразование из X 3 C в ST |C|=8

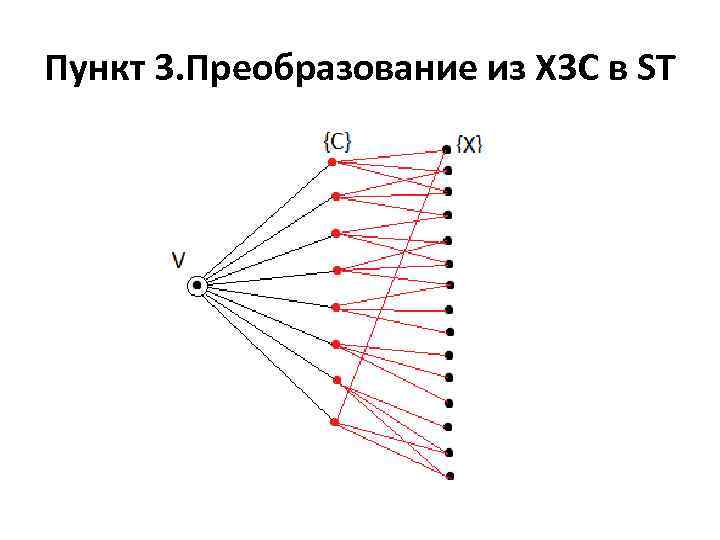Пункт 3. Преобразование из X 3 C в ST

Пункт 3. Преобразование из X 3 C в ST Условия для дерева Штайнера: • T действительно дерево: оно не содержит циклов и оно связно; • дерево T касается всех терминалов указанного множества R; • число ребер, которые включает дерево не более k. Установим K равное 4 q, где q - количество трёхэлементных подмножеств задачи Х 3 С.

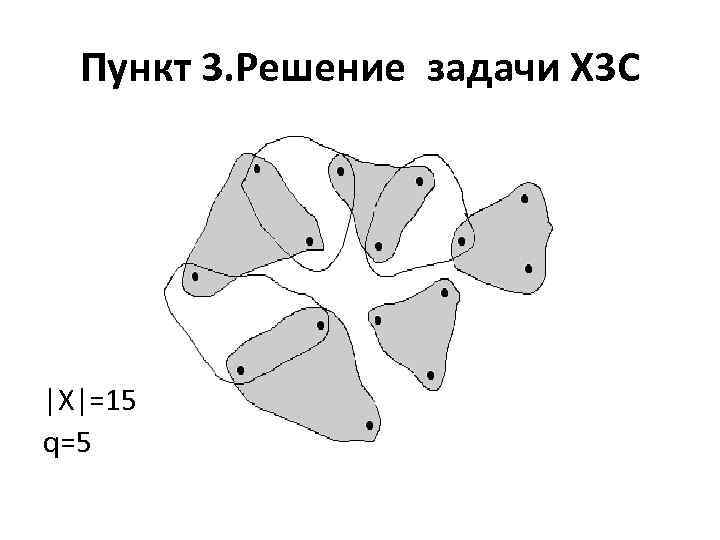Пункт 3. Решение задачи Х 3 С |X|=15 q=5

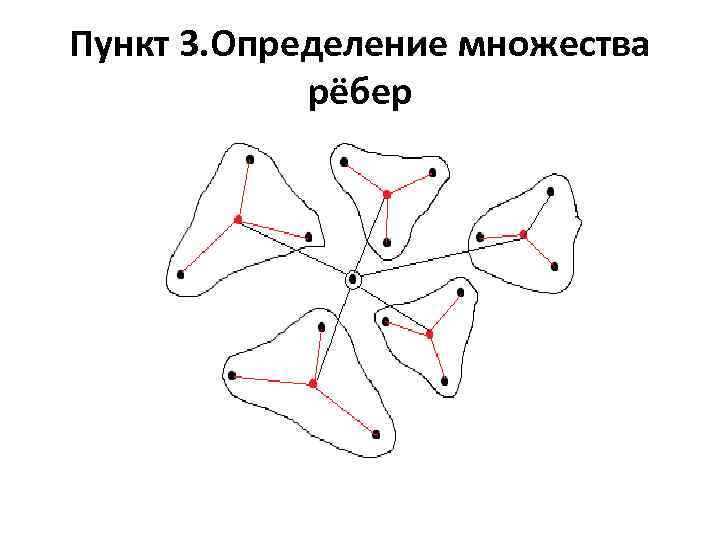Пункт 3. Определение множества рёбер

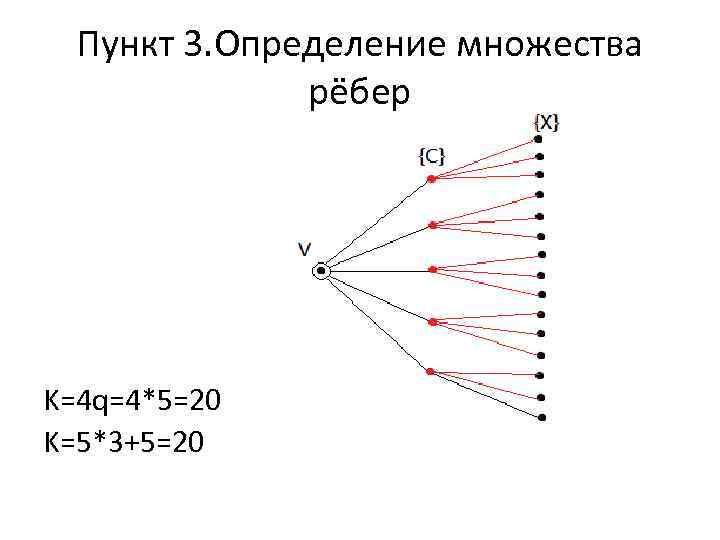Пункт 3. Определение множества рёбер K=4 q=4*5=20 K=5*3+5=20

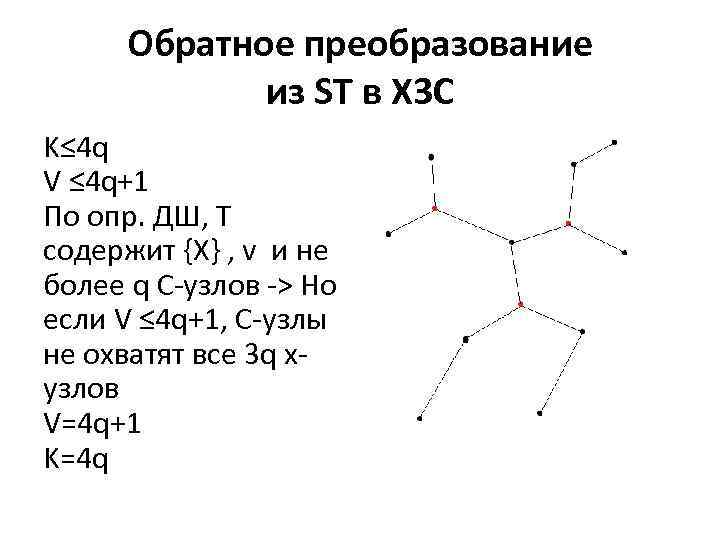Обратное преобразование из ST в Х 3 С K≤ 4 q V ≤ 4 q+1 По опр. ДШ, Т содержит {Х} , v и не более q С-узлов -> Но если V ≤ 4 q+1, С-узлы не охватят все 3 q xузлов V=4 q+1 K=4 q

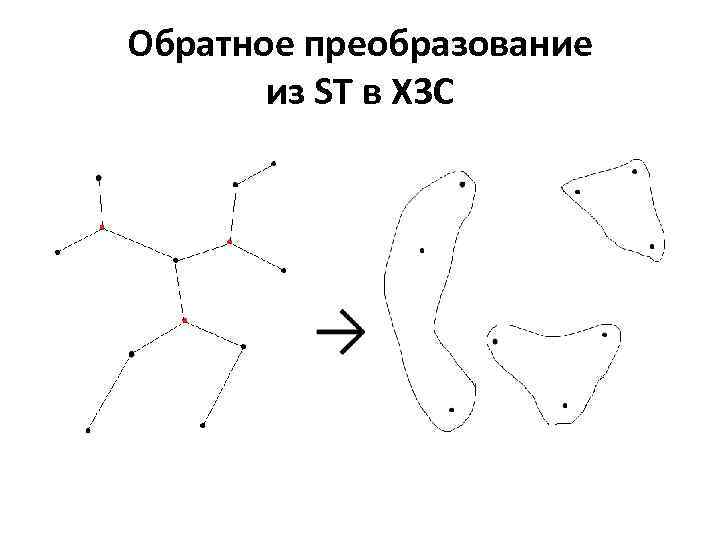Обратное преобразование из ST в Х 3 С

Алгоритм аппроксимации Robins, Zelikovsky (2000 г. ) Обозначения: Дан граф G = (V, E; cost), STP - любое дерево из G : GS представляет собой полный граф с множеством вершин S. Пусть MST (GS) минимальное остовное дерево GS. Для любого графа H, cost(H) является суммой весов всех ребер в H. Обозначаем Стоимость минимального остовного дерева Н как mst(H). Дерево Штейнера на подмножество S`, в котором все терминалы листья называется Полной компонентой. T – дерево, соединяющие каждую вершину Штейнера с терминалом. Пусть T(H) граф минимальной стоимости в , который содержит H и покрывает все терминалы. Прирост H по отношению к Т определяется loss(K) является стоимостью подключения точек Штейнера из K к терминалам.

Loss-Contracting Algorithm (k-LCA) ВХОД: полный граф G = (V; E; cost) с весом рёбер, удовлетворяющих неравенству треугольника, набором терминалов и целым ВЫХОД: k-ограниченное дерево Штайнера графа G, включающее все терминалы из S T = MST(GS) H = GS Repeat forever Поиск k-ограниченной полной компоненты K с максимальным r=gain. T(K)/loss(K) If r≤ 0 then exit repeat H = H U K T = MST(T U C[K]) Output дерево MST(H)

Время работы Loss-Contracting алгоритма в квази-двудольных графах. Loss-Contracting алгоритм может быть реализован за общее время работы O (n 2 m) , где m и n - количество терминалов и нетерминалов соответственно

Коэффициент Аппроксимации. Теорема: для любого экземпляра ST, стоимость аппроксимации ST производится с помощью алгоритма k-LCA не более чем : Approx ≈ 1+ln 3/2 <1. 55