3.6 Клики графа.ppt
- Количество слайдов: 23
 Новый подход к решению графовых задач на основе квантовых алгоритмов. Определение клик графа УЧЕБНОЕ ПОСОБИЕ ПОД РЕД. КУРЕЙЧИКА В. М. Допущено учебно-методическим объединением ВУЗов по университетскому политехническому образованию в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлениям «Информатика и вычислительная техника» и «Информационные системы» Таганрог 2012
Новый подход к решению графовых задач на основе квантовых алгоритмов. Определение клик графа УЧЕБНОЕ ПОСОБИЕ ПОД РЕД. КУРЕЙЧИКА В. М. Допущено учебно-методическим объединением ВУЗов по университетскому политехническому образованию в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлениям «Информатика и вычислительная техника» и «Информационные системы» Таганрог 2012
 Новый подход к решению графовых задач на основе квантовых алгоритмов В задаче искусственного интеллекта и других задачах оптимизации возникает необходимость получать решения NP – полных проблем с экспоненциальной временной трудностью. В последнее время появились новые подходы решения таких задач, основанные на методах квантового поиска.
Новый подход к решению графовых задач на основе квантовых алгоритмов В задаче искусственного интеллекта и других задачах оптимизации возникает необходимость получать решения NP – полных проблем с экспоненциальной временной трудностью. В последнее время появились новые подходы решения таких задач, основанные на методах квантового поиска.
 Новый подход к решению графовых задач на основе квантовых алгоритмов Квантовый поиск анализирует неструктурированные проблемы, которым в общем виде формулируются следующим образом : Задача функция f(x), аргументы X – целые числа x = 1, 2, …. , N, причем f(x) принимает значение ноль во всех случаях, кроме x=t. Необходимо найти значение t, используя наименьшее число запросов к f(x).
Новый подход к решению графовых задач на основе квантовых алгоритмов Квантовый поиск анализирует неструктурированные проблемы, которым в общем виде формулируются следующим образом : Задача функция f(x), аргументы X – целые числа x = 1, 2, …. , N, причем f(x) принимает значение ноль во всех случаях, кроме x=t. Необходимо найти значение t, используя наименьшее число запросов к f(x).
 Новый подход к решению графовых задач на основе квантовых алгоритмов Задачи такого типа при небольшом x<100 решаются на основе полного перебора (исчерпывающего поиска) или методом проб и ошибок. Например, если x=N, то в среднем потребуется O(N/2) запросов к f(x) и в худшем случае O(N-1)! запросов для нахождения x=t.
Новый подход к решению графовых задач на основе квантовых алгоритмов Задачи такого типа при небольшом x<100 решаются на основе полного перебора (исчерпывающего поиска) или методом проб и ошибок. Например, если x=N, то в среднем потребуется O(N/2) запросов к f(x) и в худшем случае O(N-1)! запросов для нахождения x=t.
 Новый подход к решению графовых задач на основе квантовых алгоритмов Изобретателем квантового алгоритма является Л. Гровер. По его идее при решении неструктурированной проблемы поиска существует “оракул”, определяющий является ли рассматриваемое решение искомым.
Новый подход к решению графовых задач на основе квантовых алгоритмов Изобретателем квантового алгоритма является Л. Гровер. По его идее при решении неструктурированной проблемы поиска существует “оракул”, определяющий является ли рассматриваемое решение искомым.
 Новый подход к решению графовых задач на основе квантовых алгоритмов Он рассматривает N целых чисел индекса x=1, 2, …, N как набор ортогональных векторов в N – размерном пространстве Гильберта.
Новый подход к решению графовых задач на основе квантовых алгоритмов Он рассматривает N целых чисел индекса x=1, 2, …, N как набор ортогональных векторов в N – размерном пространстве Гильберта.
 Новый подход к решению графовых задач на основе квантовых алгоритмов Этот шаг алгоритма, как бы на языке вычисления кванта, ставит в соответствие каждому возможному индексу уникальный собственный вектор.
Новый подход к решению графовых задач на основе квантовых алгоритмов Этот шаг алгоритма, как бы на языке вычисления кванта, ставит в соответствие каждому возможному индексу уникальный собственный вектор.
 Новый подход к решению графовых задач на основе квантовых алгоритмов Первоначально готовится пространство, , т. е. как бы квантовый регистр памяти, содержащий определенное количество суперпозиций, равное количеству всех N.
Новый подход к решению графовых задач на основе квантовых алгоритмов Первоначально готовится пространство, , т. е. как бы квантовый регистр памяти, содержащий определенное количество суперпозиций, равное количеству всех N.
 Новый подход к решению графовых задач на основе квантовых алгоритмов Для реализации поиска это квантовое пространство должно развиваться в общую суперпозицию, которая имеет амплитуду, сконцентрированную в векторе, определяющим путь до цели поиска. Предлагаемая процедура квантового кругооборота U на L=0(log 2 N).
Новый подход к решению графовых задач на основе квантовых алгоритмов Для реализации поиска это квантовое пространство должно развиваться в общую суперпозицию, которая имеет амплитуду, сконцентрированную в векторе, определяющим путь до цели поиска. Предлагаемая процедура квантового кругооборота U на L=0(log 2 N).
 Новый подход к решению графовых задач на основе квантовых алгоритмов Другими словами, если имеется отличное от нуля совпадение между стартовым пространством и целевым , то есть , тогда можно использовать унитарную процедуру U для выполнения классического поиска цели.
Новый подход к решению графовых задач на основе квантовых алгоритмов Другими словами, если имеется отличное от нуля совпадение между стартовым пространством и целевым , то есть , тогда можно использовать унитарную процедуру U для выполнения классического поиска цели.
 Новый подход к решению графовых задач на основе квантовых алгоритмов Л. Гровер предлагает использовать U и f(x), чтобы построить увеличивающий амплитуду оператор Q, который изменяет амплитуду вероятности от не – цели векторов в цель.
Новый подход к решению графовых задач на основе квантовых алгоритмов Л. Гровер предлагает использовать U и f(x), чтобы построить увеличивающий амплитуду оператор Q, который изменяет амплитуду вероятности от не – цели векторов в цель.
 Новый подход к решению графовых задач на основе квантовых алгоритмов Поведение “оракула” в алгоритме квантового поиска моделируется возвратной функцией f(x)=0, для всех x, t и f(x)=1, для x=t.
Новый подход к решению графовых задач на основе квантовых алгоритмов Поведение “оракула” в алгоритме квантового поиска моделируется возвратной функцией f(x)=0, для всех x, t и f(x)=1, для x=t.
 Новый подход к решению графовых задач на основе квантовых алгоритмов Для решения NP – полных проблем на графах предлагается анализировать структуру графа чтобы “выращивать” полные решения, рекурсивно расширяя последовательные частичные решения.
Новый подход к решению графовых задач на основе квантовых алгоритмов Для решения NP – полных проблем на графах предлагается анализировать структуру графа чтобы “выращивать” полные решения, рекурсивно расширяя последовательные частичные решения.
 Новый подход к решению графовых задач на основе квантовых алгоритмов В задачах на графах важным является нахождение инвариантов. Инвариант графа G=(X, U), |X|=U, |U|=m, это число, связанное с G, которое принимает одно и то же значение на любом графе, изоморфном G. Очевидно, что число вершин U и ребер q является простейшими инвариантами графа.
Новый подход к решению графовых задач на основе квантовых алгоритмов В задачах на графах важным является нахождение инвариантов. Инвариант графа G=(X, U), |X|=U, |U|=m, это число, связанное с G, которое принимает одно и то же значение на любом графе, изоморфном G. Очевидно, что число вершин U и ребер q является простейшими инвариантами графа.
 Новый подход к решению графовых задач на основе квантовых алгоритмов Полный набор инвариантов определяет граф с точностью до изоморфизма. Основными инвариантами графа является числа: цикломатическое, хроматическое, внешней и внутренней устойчивости, клик , ядер, планарности и т. д.
Новый подход к решению графовых задач на основе квантовых алгоритмов Полный набор инвариантов определяет граф с точностью до изоморфизма. Основными инвариантами графа является числа: цикломатическое, хроматическое, внешней и внутренней устойчивости, клик , ядер, планарности и т. д.
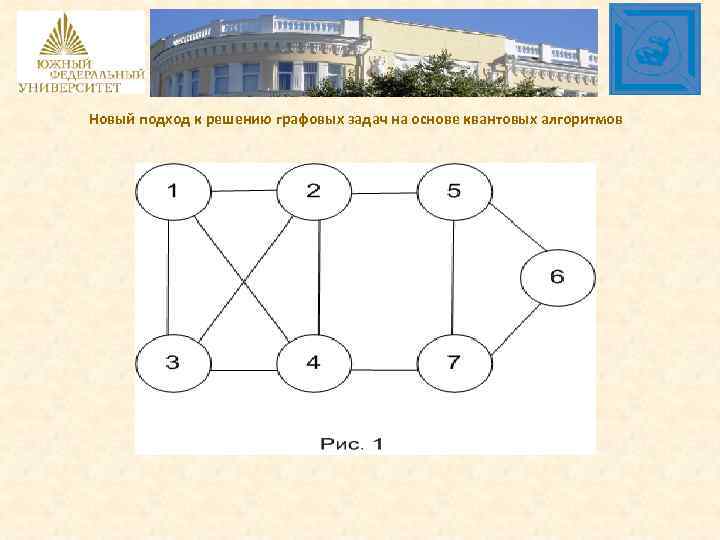
 Новый подход к решению графовых задач на основе квантовых алгоритмов Покажем на примере графа на рис. 1 определенные числа клик на основе квантового алгоритма. Клика – это полный подграф, содержащий наибольшее число ребер. Соответственно число полноты это наибольшее число вершин в клике.
Новый подход к решению графовых задач на основе квантовых алгоритмов Покажем на примере графа на рис. 1 определенные числа клик на основе квантового алгоритма. Клика – это полный подграф, содержащий наибольшее число ребер. Соответственно число полноты это наибольшее число вершин в клике.
 Новый подход к решению графовых задач на основе квантовых алгоритмов
Новый подход к решению графовых задач на основе квантовых алгоритмов
 Новый подход к решению графовых задач на основе квантовых алгоритмов Например, при определении клик графа мы должны найти частичные решения для каждой вершины графа рекурсивно расширяя “хорошие” решения, устраняя тупиковые решения.
Новый подход к решению графовых задач на основе квантовых алгоритмов Например, при определении клик графа мы должны найти частичные решения для каждой вершины графа рекурсивно расширяя “хорошие” решения, устраняя тупиковые решения.
 Новый подход к решению графовых задач на основе квантовых алгоритмов На первом шаге для вершины 1 получим следущее частичные решения: {1, 2}, {1, 3}, {1, 4}; 1 уровень {1, 2, 3}, {1, 2, 4}, {1, 3, 4}; 2 уровень {1, 2, 3, 4} 3 уровень
Новый подход к решению графовых задач на основе квантовых алгоритмов На первом шаге для вершины 1 получим следущее частичные решения: {1, 2}, {1, 3}, {1, 4}; 1 уровень {1, 2, 3}, {1, 2, 4}, {1, 3, 4}; 2 уровень {1, 2, 3, 4} 3 уровень
 Новый подход к решению графовых задач на основе квантовых алгоритмов В результате после суперпозиции частичных решений получим клику Q 1={1, 2, 3, 4}, |Q 1| = 4. На втором шаге для вершины 2 получим: {2, 5}, Q 2=2 Для третьей вершины частичных решений нет.
Новый подход к решению графовых задач на основе квантовых алгоритмов В результате после суперпозиции частичных решений получим клику Q 1={1, 2, 3, 4}, |Q 1| = 4. На втором шаге для вершины 2 получим: {2, 5}, Q 2=2 Для третьей вершины частичных решений нет.
 Новый подход к решению графовых задач на основе квантовых алгоритмов Для четвертой вершины имеем {4, 7}, Q 3={4, 7}, | Q 3|=2. Для пятой вершины получим следующие частичные решения {5, 6}, {5, 7} 1 уровень {5, 6, 7} 2 уровень После супер позиции частичных решений получим клику Q 4 ={5, 6, 7} |Q 4 |=3.
Новый подход к решению графовых задач на основе квантовых алгоритмов Для четвертой вершины имеем {4, 7}, Q 3={4, 7}, | Q 3|=2. Для пятой вершины получим следующие частичные решения {5, 6}, {5, 7} 1 уровень {5, 6, 7} 2 уровень После супер позиции частичных решений получим клику Q 4 ={5, 6, 7} |Q 4 |=3.
 Новый подход к решению графовых задач на основе квантовых алгоритмов Итак для графа G (рис. 1) построено семейство клик Q={ Q 1, Q 2 , Q 3 , Q 4}. Причем число полноты графа равно 4.
Новый подход к решению графовых задач на основе квантовых алгоритмов Итак для графа G (рис. 1) построено семейство клик Q={ Q 1, Q 2 , Q 3 , Q 4}. Причем число полноты графа равно 4.
 Новый подход к решению графовых задач на основе квантовых алгоритмов В заключении отметим, что квантовый поиск может ускорить классический случайный алгоритм создавая суперпозиции частичных решений увеличивая пространство поиска искомого решения.
Новый подход к решению графовых задач на основе квантовых алгоритмов В заключении отметим, что квантовый поиск может ускорить классический случайный алгоритм создавая суперпозиции частичных решений увеличивая пространство поиска искомого решения.


