НОВЫЕ ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ Подготовили ученицы 7 К

НОВЫЕ ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ. Подготовили ученицы 7 «К» класса Агеева Алиса и Кисляковой Анна Руководитель Капник Е. В.

ВВЕДЕНИЕ. Цели работы : Сформулировать и доказать новые признаки равенства треугольников. Обосновать эффективность применения новых признаков равенства треугольников при решении геометрических задач. Гипотеза : Существование новых признаков равенства треугольников. Методы исследования : Доказание равенства треугольников по новым признакам, опираясь на старые.

ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ, С КОТОРЫМИ МЫ УЖЕ ЗНАКОМЫ. • 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. • 2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. • 3. если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

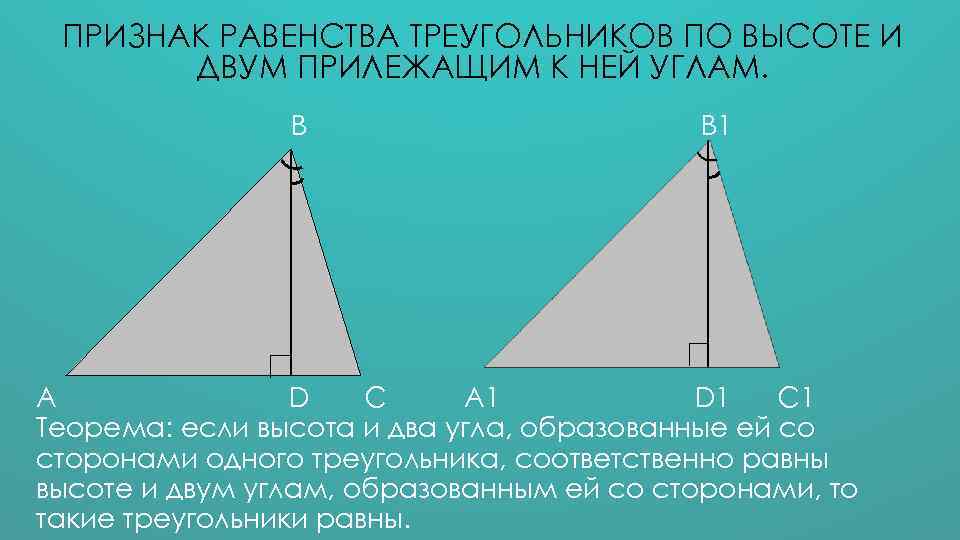ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ ПО ВЫСОТЕ И ДВУМ ПРИЛЕЖАЩИМ К НЕЙ УГЛАМ. В В 1 А D С А 1 D 1 С 1 Теорема: если высота и два угла, образованные ей со сторонами одного треугольника, соответственно равны высоте и двум углам, образованным ей со сторонами, то такие треугольники равны.

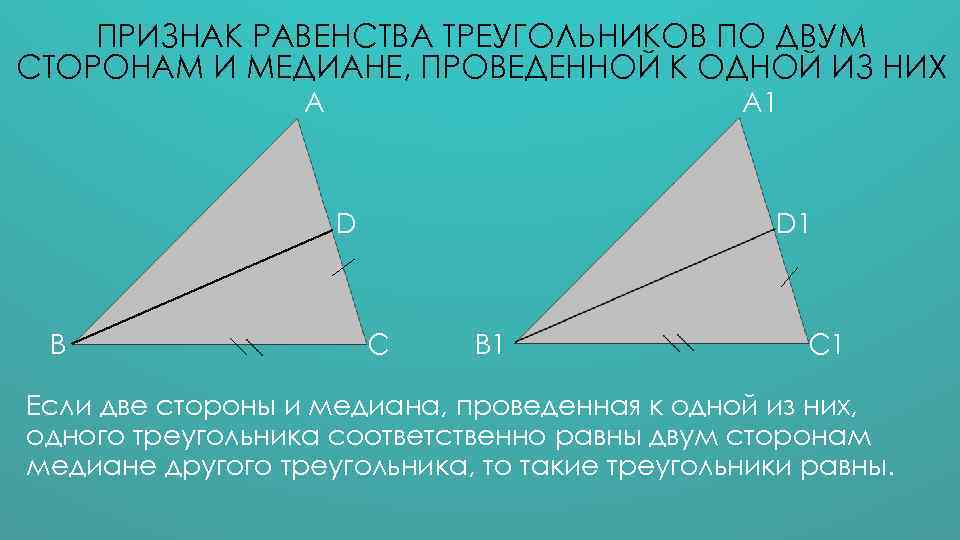ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ ПО ДВУМ СТОРОНАМ И МЕДИАНЕ, ПРОВЕДЕННОЙ К ОДНОЙ ИЗ НИХ А А 1 D В D 1 С В 1 С 1 Если две стороны и медиана, проведенная к одной из них, одного треугольника соответственно равны двум сторонам медиане другого треугольника, то такие треугольники равны.

ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ ПО БИССЕКТРИСЕ И ДВУМ УГЛАМ.

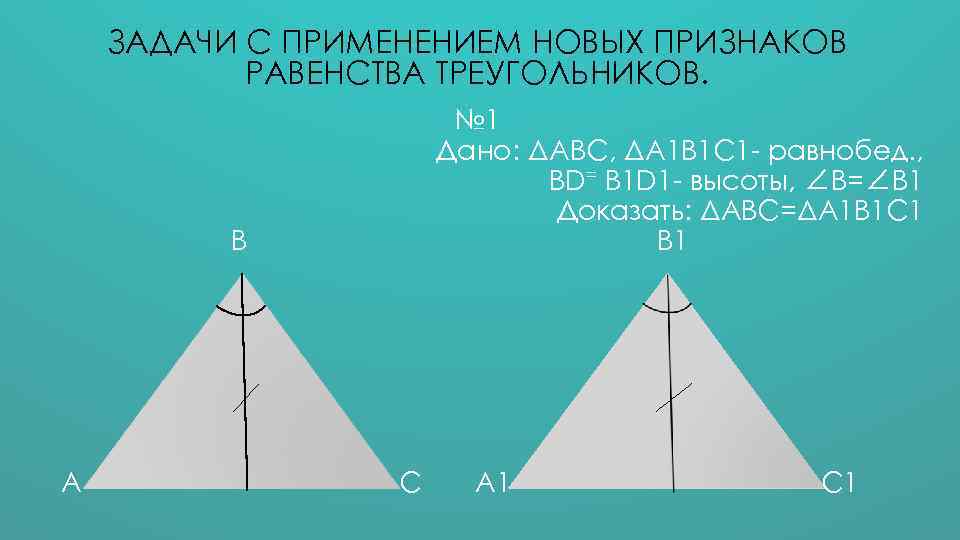ЗАДАЧИ С ПРИМЕНЕНИЕМ НОВЫХ ПРИЗНАКОВ РАВЕНСТВА ТРЕУГОЛЬНИКОВ. № 1 Дано: ΔАВС, ΔА 1 В 1 С 1 - равнобед. , ВD= В 1 D 1 - высоты, ∠В=∠В 1 Доказать: ΔАВС=ΔА 1 В 1 С 1 В А С А 1 С 1

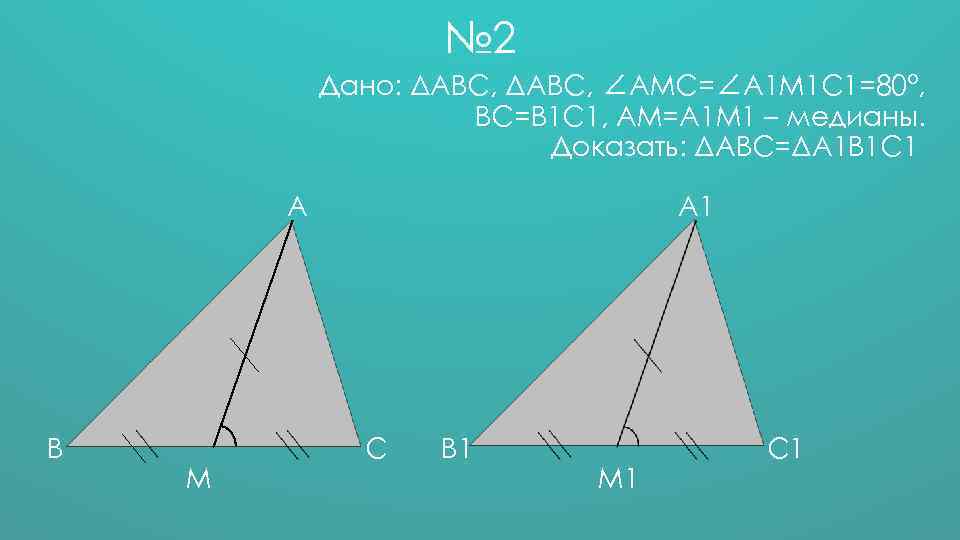№ 2 Дано: ΔАВС, ∠АМС=∠А 1 М 1 С 1=80°, ВС=В 1 С 1, АМ=А 1 М 1 – медианы. Доказать: ΔАВС=ΔА 1 В 1 С 1 А В М А 1 С В 1 М 1 С 1