Новые подходы к вопросам геолого гидродинамического моделирования

«Новые подходы к вопросам геолого гидродинамического моделирования» © ООО «РН -Уфа. НИНИнефть» Байков В. А. , …

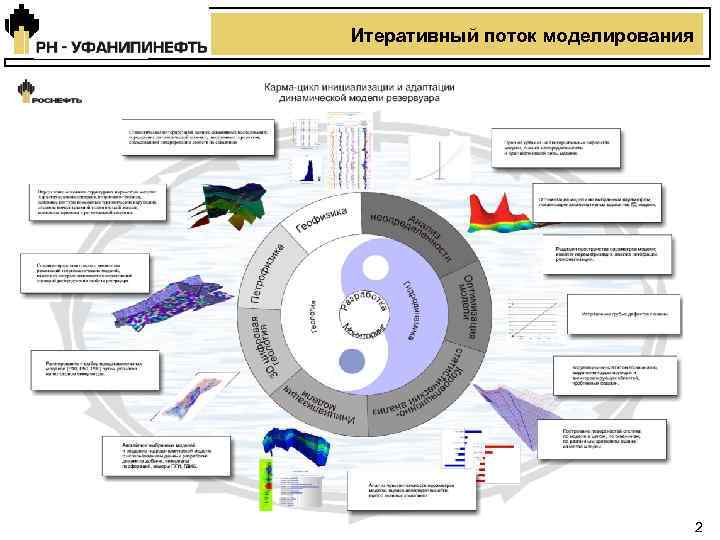Итеративный поток моделирования 2

Общие принципы моделирования Модель – это хорошая карикатура процесса. • Я. Френкель Непротиворечивость Результаты измерений, полученные отдельными элементами модели, не должны противоречить другу. • Полнота Внутри данного класса экспериментов все результаты измерений должны быть (по крайней мере, в принципе) предсказуемы. • Независимость В модели в качестве основополагающих должны присутствовать только такие параметры состояния и законы, которые не могут быть математически или логически (методом дедукции) выведены из других величин или законов. • Категориальность Различные представления модели должны быть преобразуемы друг в друга путем взаимно однозначных отображений (ковариантность). • Объективность Временные изменения состояния системы зависят, по существу, лишь от состояния самой системы и параметров обмена • Делимость Каждая система может быть разложена на две подсисте мы, взаимодействующие посредством процессов обмена. В обеих под системах действительны одни и те же параметры состояния и законы движения. Результаты будущих измерений не зависят от того, каким образом произведено разделение на подсистемы. 3

Прелюдия Геология – область науки, с огромным масштабом неопределенности управляющих физических законов. Поэтому часто говорят, геология - наука гуманитарная. Гуманитарная наука описывает не то, что существует в действительности, а то, что человек воспринимает и на что реагирует. Лев Гумилев, Древняя Русь и Великая степь Предсказание некоего события в чувственном мире всегда сопряжено с определенной долей неуверенности, тогда как все события, описываемые физической картиной мира, протекают в согласии с определенными установленными законами. Макс Планк. Пути физического познания 4

Вычислимость В любой достаточно сложной непротиворечивой теории существует утверждение, которое средствами самой теории невозможно ни доказать, ни опровергнуть. Например, такое утверждение можно добавить к системе аксиом, оставив её непротиворечивой. Курт Гёдель, 1931 гг. Истинность (непротиворечивость) или ложность некоторых утверждений установить невозможно, потому что задача принятия решений будет невероятно длинной - проблема вычислимости Д. Рюэль «Случайность и Хаос» Для тех, кто не умеет считать – дорога невероятно длинная. Для тех, кто умеет – дорога будет конечной. 5

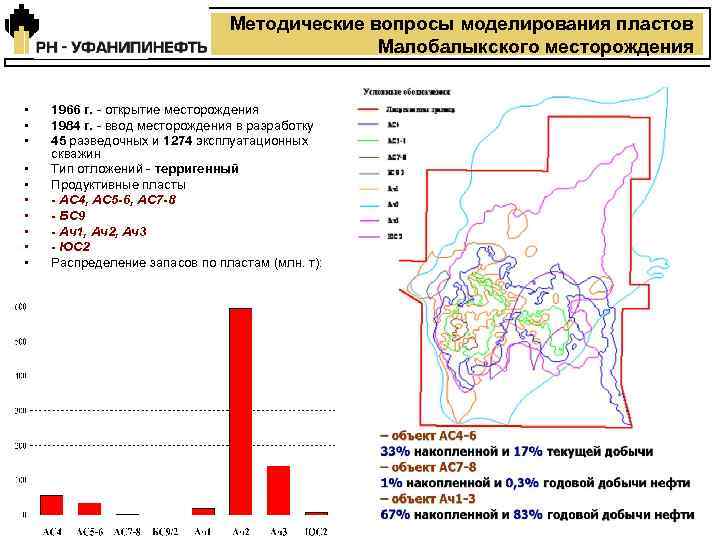Методические вопросы моделирования пластов Малобалыкского месторождения • • • 1966 г. - открытие месторождения 1984 г. - ввод месторождения в разработку 45 разведочных и 1274 эксплуатационных скважин Тип отложений - терригенный Продуктивные пласты - АС 4, АС 5 -6, АС 7 -8 - БС 9 - Ач1, Ач2, Ач3 - ЮС 2 Распределение запасов по пластам (млн. т): 6

Покачевский клиноциклит. Региональный проект. Ачимовские отложения 7

Схема распространения литотипов и концептуальная модель строения покачевского клиноциклита пласта Aч2 ПК 8

Детальная корреляция пласта Ач2 цикл 1 цикл 2 цикл 3 цикл 4 цикл 5 9

Определение пористости • По данным керна (с привлечением новых) и кривым ЯМК провели две зависимости Кпо=f( ПС) – верхний предел по керну и средние значения по ЯМК Кпо, д. ед. Керн ЯМК Из ПЗ 2009 Рекомендуемые ПС • Значения Кпо были пересчитаны в пластовые условия для Ач1 -2 Кпо_пл=Кпо-0, 006 для Ач3 Кпо_пл=0, 91*Кпо+0, 5 10

Основания математической модели в геостатистике 1. Гипотеза стационарности -инвариантность к трансляции в пространстве 2. Изотропность --- зависимость только от расстояния (геометрическая анизотропия – сжатие+поворот изотропия) 3. Эргодичность --- пространственное среднее - есть среднее по времени 4. Природа случайного поля (гаус. проц. ). . . 11

Вопрос ослабления основных ограничений Возможно ли: 1. отказаться от стационарности (подразумевается обобщение модели тренд плюс стационарный остаток) и гауссовости? 2. снять условие изотропности и геометрической анизотропии (разные вариограммы во всех направлениях)? 3. исключить параметрический анализ вариограмм (сколь угодно много моделей вариограмм, выбираются автоматически)? Ответ: ДА! 12

Допущение о стационарности Стационарность второго порядка (Слабая) • Среднее и дисперсия не зависят от местоположения точки • Ковариация значений в двух точках зависит только от расстояния между ними вариограмма 13

СТАЦИОНАРНОСТЬ ПРОТИВ НЕСТАЦИОНАРНОСТИ Стационарная модель 5000 Тренда нет 500 Дисперсия не изменяется 14

СТАЦИОНАРНОСТЬ ПРОТИВ НЕСТАЦИОНАРНОСТИ Нестационарный случай Тренд есть Дисперсия постоянна Тренд+Стационарная переменная … … … 15

КОВАРИАЦИЯ И ВАРИОГРАММА СТАЦИОНАРНОСТЬ ПРОТИВ НЕСТАЦИОНАРНОСТИ Нестационарный случай … … … , Тренда нет Дисперсия изменяется Тренд есть Дисперсия изменяется 16

2. Изотропность- Случайное поле зависит от одоной переменной, а именно от «расстояния» - 3. Эргодичность --- пространственное среднее - есть среднее по времени 17

Наиболее часто используемые непрерывные модели вариограмм 18

«Экзотические» , но важные модели вариограмм 19

Различные вариограммы, и их интерпретации фрактал «Эффект ямы» 20

Различные вариограммы, и их интерпретации Эффект самородков (шум) 21

Данные по скважинам: (ПС) 22

Вариограммы (Petrel), ALSP 23

Нестационарность, анизотропия ALPS Petrel Учет влияния нестационарности и анизотропии 24

Нестационарность, анизотропия ALPS Petrel Учет влияния нестационарности и анизотропии 25

Учет влияния анизотропии 26

3 D Геология: Принципы прекрасного + принципа конструктивности 27

3 D Геология: Принцип конструктивизма +принцип прекрасного 28

Радиус вариограммы: пример неопределенности В рамках существующей неопределенности входных данных возможно три вероятных радиуса вариограммы: VR 1 = 500 м. VR 2 = 1000 м. VR 3 = 2000 м. С точки зрения статистики все три радиуса подходят для описания пространственного взаимодействия исходных данных. Однако радиус вариограммы оказывает влияние на размер и связность песчаных тел, и, следовательно, на гидродинамические свойства модели. Таким образом, мы получаем три равновероятных радиуса вариограммы, чувствительность которых не может быть оценена в рамках геологической модели. 29

Характеристики геологических тел на примере Приобского месторождения Пласт АС-10, Куст 141 Сферические вариограммы gx= 800 м gy= 600 м gz= 1. 2 м Nugget = 0. 01 30

Расположение тел в модели Самое крупное тело в модели 31

Тело № 1 ФР=2. 40 Vтела/Vколлектора=0. 44 КИН(Т=25 лет)=9. 5 % Самое крупное тело в модели 32

Тело № 4 ФР=2. 22 Vтела/Vколлектора=0. 04 КИН(Т=25 лет)=5. 2% Самое крупное тело в модели 33

Тело № 8 ФР=1. 9 Vтела/Vколлектора=0. 007 КИН(Т=25 лет)=0 % Самое крупное тело в модели 34

Расчеты на 3 D и 2 D симуляторах 3 D численная гидродинамическая модель Время расчета (~100)*мин Расчеты на кластере 2 D аналитическая модель Время расчета (~1)*мин. Расчеты на ПК 35

3 D и 2 D модели Трехмерная ГДМ Необходим метод учета геологической неоднородности Двумерная аналитическая ГДМ для корректного перехода от 3 D к 2 D моделям Учет 3 D неоднородности + скорость расчета 2 D симулятора оптимальный (КИН, экономика) и обоснованный выбор системы разработки в короткие сроки 36

Гидродинамические характеристики геологической неоднородности • Геометрия песчаных тел в геологической модели характеризуется распределением длин трубок тока • Пространственная неоднородность в 3 D геологической модели может быть включена в 2 D аналитическую модель с помощью зависимости коэффициента охвата от длины линии тока • Статистические свойства распределения длин трубок тока в трехмерной гидродинамической модели могут использоваться для сравнения стохастических реализаций геологической модели 37

Переход от численных 3 D ГДМ к 2 D аналитическим моделям на основе линий тока 2 D однородная гидродинамическая модель Расстояние между рядами 400 м 38

Переход от численных 3 D ГДМ к 2 D аналитическим моделям на основе линий тока 3 D гидродинамическая модель Расстояние между рядами 400 м 39

Переход от численных 3 D ГДМ к 2 D аналитическим моделям на основе линий тока 3 D Шаг 1 2 D Шаг 2 40

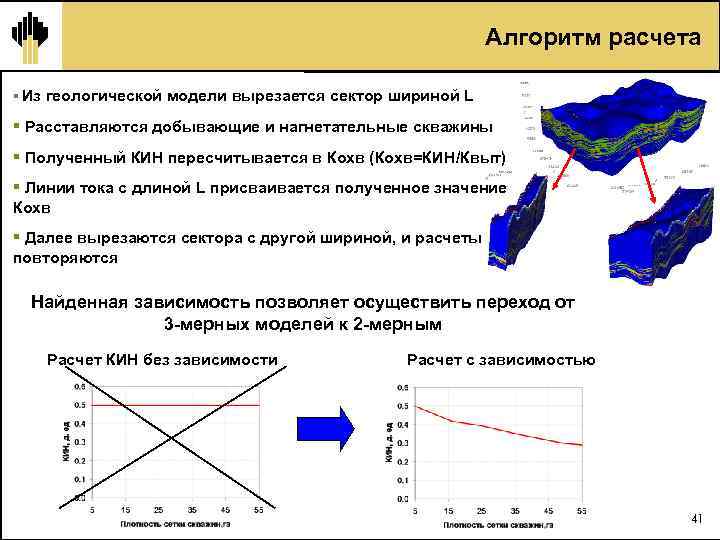Алгоритм расчета § Из геологической модели вырезается сектор шириной L § Расставляются добывающие и нагнетательные скважины § Полученный КИН пересчитывается в Кохв (Кохв=КИН/Квыт) § Линии тока с длиной L присваивается полученное значение Кохв § Далее вырезаются сектора с другой шириной, и расчеты повторяются Найденная зависимость позволяет осуществить переход от 3 мерных моделей к 2 мерным Расчет КИН без зависимости Расчет с зависимостью 41

Зависимость Кохв от длины линии тока Зависимость Кохв (L) получена из сектора существующей геологической модели. Параметры геологической модели: § Размер ячеек 100 x 0. 4 м § Радиус вариограммы для литологии 1100 и 900 м, азимут 25 0 § Песчанистость 18 % § Для получения зависимости рассчитано 69 секторных моделей Итоговая зависимость Кохв от длины линии тока § Процент падения Кохв составляет 21% § Дисперсия составляет 4*10 4 § Дисперсия говорит о неоднородности геологической модели 42

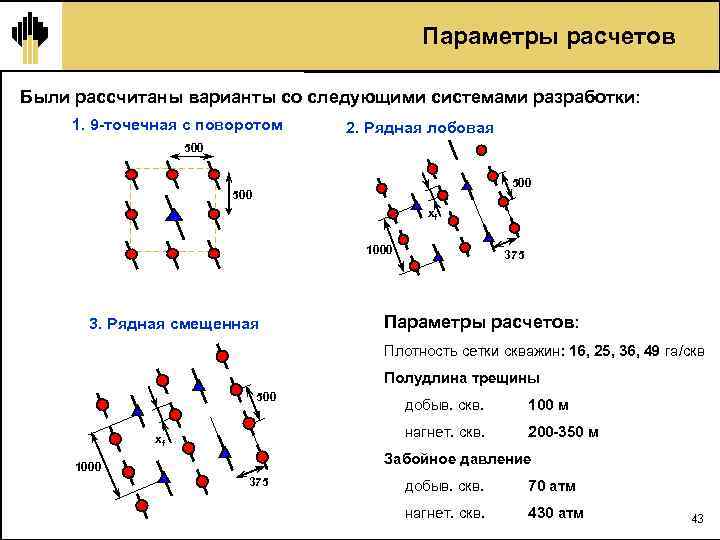Параметры расчетов Были рассчитаны варианты со следующими системами разработки: 1. 9 точечная с поворотом 2. Рядная лобовая 500 500 xf 1000 3. Рядная смещенная 375 Параметры расчетов: Плотность сетки скважин: 16, 25, 36, 49 га/скв Полудлина трещины 500 100 м нагнет. скв. xf добыв. скв. 200 350 м Забойное давление 1000 375 добыв. скв. 70 атм нагнет. скв. 430 атм 43

Результаты расчетов По результатам модельных расчетов получены следующие зависимости: 500 x 375 (25 га/скв) 600 x 450 (36 га/скв) 700 x 700 400 x 300 (16 га/скв) 400 x 400 700 x 525 (49 га/скв) Результаты расчета рядных систем (лобовая и смещенная) показывают одинаковые результаты Максимальный NPV для всех рассмотренных систем достигается при плотности 25 га/скв (3. 06 млн. руб/га) Рядные системы по сравнению с 9 точечной показывают лучшие значения КИН при одинаковых NPV (повышение NPV для 9 точечной системы связано с бо льшим количеством добывающих скважин при одинаковой плотности) Для рядных систем при уплотнении с 25 до 16 га/скв КИН увеличивается с 0. 405 до 0. 411, при этом NPV снижается с 3. 06 до 2. 8 млн/га 44

Динамика дебитов и обводненности § Обводнение для рядных систем и 9 точки (25 га) происходит одинаково первые 6 лет (до обв. 65%) § Далее на рядных системах происходит ускоренное обводнение из за приближения зоны отбора и закачки (рядная система - 375 м между доб. и нагн. рядами, 9 -точка 500 между скважинами) § Добыча нефти на скважину для рядных систем выше из за приближения зоны отбора и закачки § Первые 1. 5 года у 9 точки с плотностью 16 га средний дебит нефти выше, чем в случае плотности 25 га. § Далее средний дебит нефти при плотности 16 га/скв 45 падает из за резкого роста обводненности

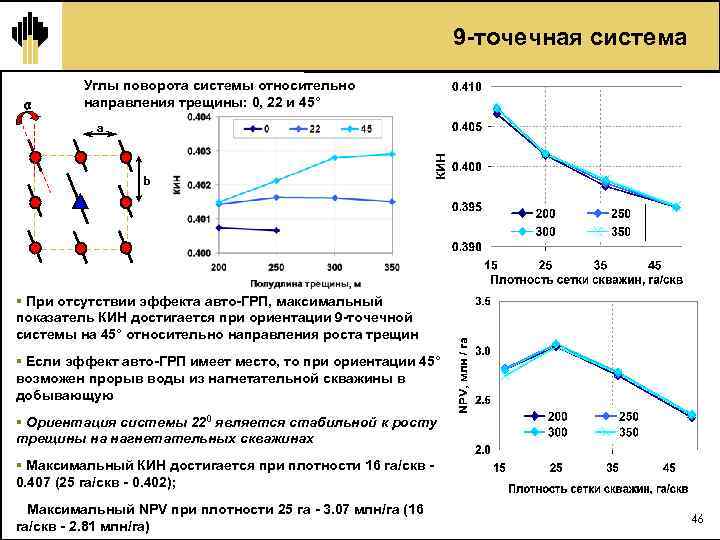9 точечная система α Углы поворота системы относительно направления трещины: 0, 22 и 45° a b § При отсутствии эффекта авто ГРП, максимальный показатель КИН достигается при ориентации 9 точечной системы на 45° относительно направления роста трещин § Если эффект авто ГРП имеет место, то при ориентации 45° возможен прорыв воды из нагнетательной скважины в добывающую § Ориентация системы 220 является стабильной к росту трещины на нагнетательных скважинах § Максимальный КИН достигается при плотности 16 га/скв 0. 407 (25 га/скв 0. 402); Максимальный NPV при плотности 25 га 3. 07 млн/га (16 га/скв 2. 81 млн/га) 46

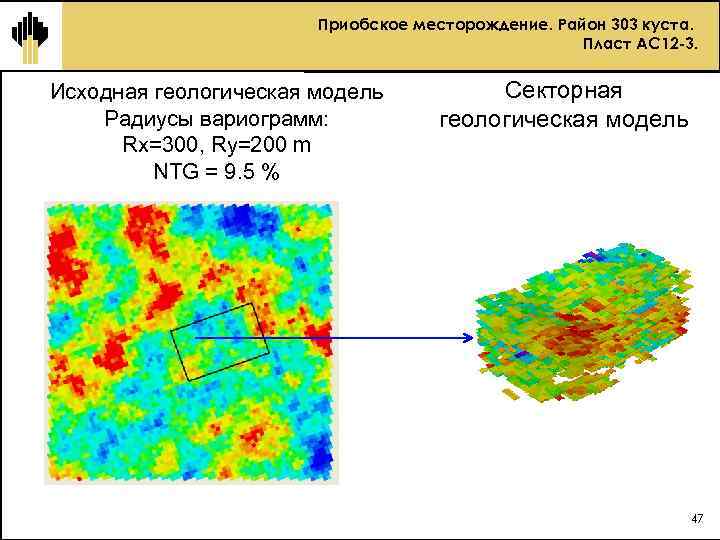Приобское месторождение. Район 303 куста. Пласт АС 12 -3. Исходная геологическая модель Радиусы вариограмм: Rx=300, Ry=200 m NTG = 9. 5 % Секторная геологическая модель 47

Приобское месторождение. Район 303 куста. Пласт АС 12 -3. ∆ Кохв = 0. 33 Кохв = 0. 44, расстояние между рядами 300 м Кохв = 0, расстояние между рядами 1400 м Падение Кохв. говорит о гидродинамической несвязанности геологических тел Для апскейленной до 1 слоя модели Кохв=0. 79, что почти в 2 раза больше, чем в исходной геологической модели. 48

Приобское месторождение. Район 303 куста. Пласт АС 12 -3. Средняя длина линий тока Расстояние между рядами 500 м Среднее значение 625 м Расстояние между рядами 1300 м Среднее значение 1682 м 49

Вместо послесловия Возникновению новых теорий предшествует период резко выраженной профессиональной неуверенности. Вероятно, такая неуверенность порождается постоянной неспособностью нормальной науки решать ее головоломки в той мере, в какой она должна это делать. Банкротство существующих правил означает прелюдию к поиску новых. Т. Кун Доблесть ума заключается не в том, чтобы быть осторожным и избегать ошибок, а в том, чтобы бескомпромиссно устранять их. Имре Лакатос 50

Спасибо за внимание 51