November 2009 Paper 3 11 Bearings

Зарегистрируйтесь, чтобы просмотреть полный документ!

November 2009 Paper 3

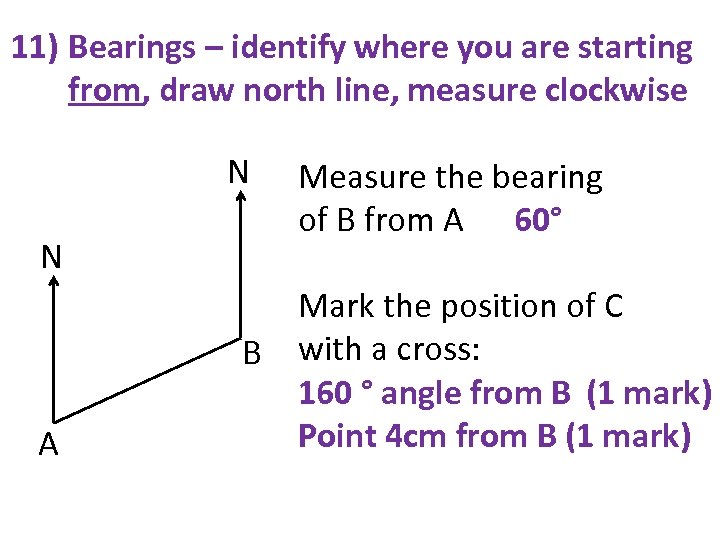
11) Bearings – identify where you are starting from, draw north line, measure clockwise N N A Measure the bearing of B from A 60° Mark the position of C B with a cross: 160 ° angle from B (1 mark) Point 4 cm from B (1 mark)

12) Batteries are sold in packets and boxes. Each packet contains 4 batteries. Each box contains 20 batteries. Bill buys p packets of batteries and b boxes of batteries. Bill buys a total of N batteries. Write down a formula for N in terms of p and b N = 4 p + 20 b Hint: make up values for p and b and work out what sum you would need to do

13) (a) Write in standard form 213 000 2. 13 x 105 (b) Write in standard form 0. 00123 1. 23 x 10 -3

14) (a) Write down the value of 50 anything to the power 0 = 1 (b) Write down the value of 2– 1 a negative power means ‘one over’ 2 -1 = ½ 21

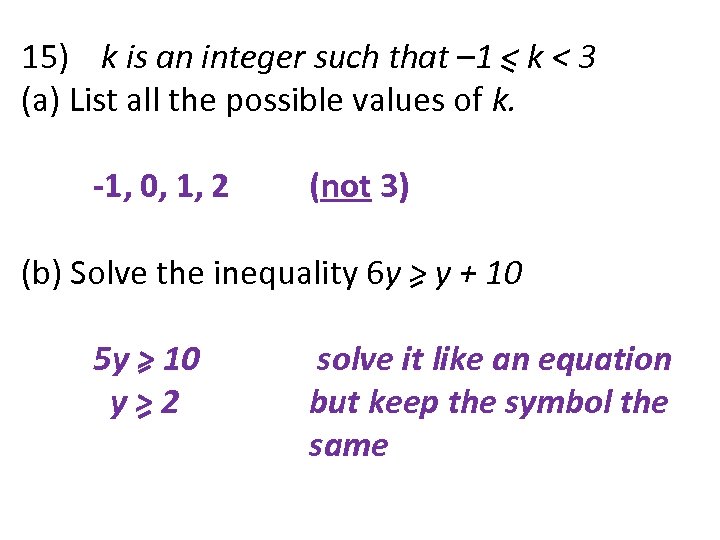
15) k is an integer such that – 1 < k < 3 (a) List all the possible values of k. -1, 0, 1, 2 (not 3) (b) Solve the inequality 6 y > y + 10 5 y > 10 y>2 solve it like an equation but keep the symbol the same

16) Make q the subject of the formula 5(q + p) = 4 + 8 p Give your answer in its simplest form. 5 q + 5 p = 4 + 8 p 5 p = 4 + 3 p 5 (one mark for expanding the bracket) (one mark for putting the ps together) final mark for isolating p

17) (a) What is the highest mark in the English test? 50 (b) Compare the distributions of the marks in the English test and marks in the Maths test. One comment must relate to the medians e. g. the median was higher for English so students did better in English. One comment must relate to the inter-quartile range e. g. the IQR is smaller for maths so the results weren’t as spread out

18) (a) Find the size of angle ABD. Give a reason for your answer. 55° (1 mark) tangent is perpendicular to a radius (1 mark) (b) Find the size of angle DEB. Give a reason for your answer. 55° (1 mark) either alternate segment theorem or angle in a semicircle and angles in a triangle (1 mark)

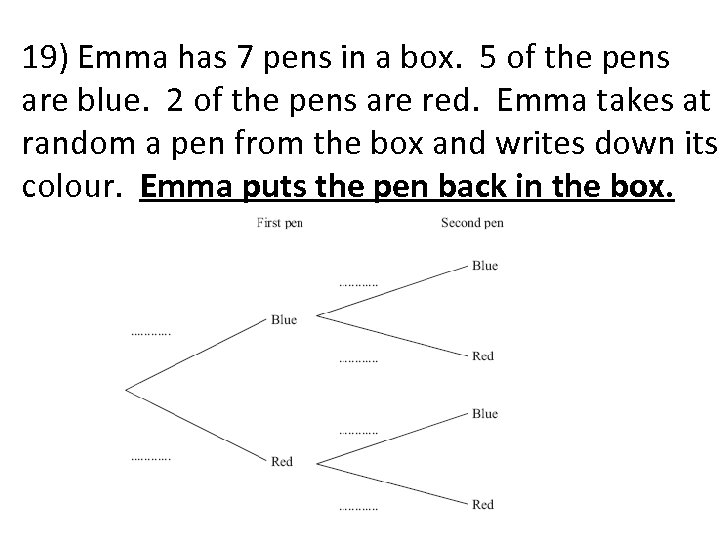
19) Emma has 7 pens in a box. 5 of the pens are blue. 2 of the pens are red. Emma takes at random a pen from the box and writes down its colour. Emma puts the pen back in the box.

19 b) Work out the probability that Emma takes exactly one pen of each colour from the box. Blue and red 5/ x 2/7 = 10/49 7 2/ x 5/7 = 10/49 7 or Red and blue 10/ + 10/49 = 20/49 49 ‘and’ means ‘x’, ‘or’ means ‘+’

20) Solve the simultaneous equations 4 x + y = -1 (1) 4 x – 3 y = 7 (2) (1)x 3 12 x + 3 y = -3 4 x – 3 y = 7 16 x = 4/16 = ¼ in (1) 1 + y = -1 y = -2 Make the ys the same Same signs subtract (our signs are different so we add)

21) Work out (2 + 3)(2 – 3) Give your answer in its simplest form. Use bird face/smiley face/FOIL 4 – 2 3 + 2 3 – 3 = 1

22) (a) Find the vector AB in terms of a and b. -a + b P is the point on AB so that AP : PB = 2 : 1 (b) Find the vector OP in terms of a and b. Give your answer in its simplest form. OA + 2/3 AB = a + 2/3(-a + b) = a - 2/3 a + 2/3 b = 1/3 a + 2/3 b

23) Prove that the recurring decimal 0. 36 = 4/11 x = 0. 3636…. 100 x = 36. 3636… 99 x = 36 = 4 99 11

24) (a) Write down the coordinates of the minimum point of the curve with the equation y = f(x – 2) (5, -4) (b) Write down the coordinates of the minimum point of the curve with the equation y = f(x + 5) + 6 (-2, 2)

25) Prove, using algebra, that the sum of two consecutive whole numbers is always an odd number. n = + 2 n + 1 (n + 1) (1 mark) Therefore it is always an odd number (1 mark)

Скачать презентацию November 2009 Paper 3 11 Bearings

7956dd46f9dbe5989da20ec79f1afae1.ppt

Количество слайдов: 21