dee42145ee329b45e57a547eea937cce.ppt
- Количество слайдов: 35
 Notes 8: Predicate logic and inference ICS 270 a Spring 2003
Notes 8: Predicate logic and inference ICS 270 a Spring 2003
 Outline w New ontology n objects, relations, properties, functions. w New Syntax n Constants, predicates, properties, functions w New semantics n meaning of new syntax w Inference rules for Predicate Logic (FOL) n Resolution n Forward-chaining, Backword-chaining n unification w Readings: Nillson’s Chapters 15 -16, Russel and Norvig Chapter 8, chapter 9
Outline w New ontology n objects, relations, properties, functions. w New Syntax n Constants, predicates, properties, functions w New semantics n meaning of new syntax w Inference rules for Predicate Logic (FOL) n Resolution n Forward-chaining, Backword-chaining n unification w Readings: Nillson’s Chapters 15 -16, Russel and Norvig Chapter 8, chapter 9
 Propositional logic is not expressive w Needs to refer to objects in the world, w Needs to express general rules n On(x, y) ~ clear(y) n All man are mortal n Everyone who passed age 21 can drink n One student in this class got perfect score n Etc…. w First order logic, also called Predicate calculus allows more expressiveness
Propositional logic is not expressive w Needs to refer to objects in the world, w Needs to express general rules n On(x, y) ~ clear(y) n All man are mortal n Everyone who passed age 21 can drink n One student in this class got perfect score n Etc…. w First order logic, also called Predicate calculus allows more expressiveness
 Syntax w Components n Infinite set of object constants, alphanumerc strings w Bb, 12345, Jerusalem, 270 a, Irvine n Function constants of all aritys (convention: start with lower case) w mother. Of, times, greater. Than, color n Relation constants, Predicates of all aritys (start with capital) w B 21, Parent, multistoried, XYZ, prime w Terms n n An object constant is a term A function constant of arity n followed by n terms in parenthesis is a term (called functional expression) w mother. Of(Silvia), Sam, leftlegof(John), add 1(5), times(5, plus(3, 6))
Syntax w Components n Infinite set of object constants, alphanumerc strings w Bb, 12345, Jerusalem, 270 a, Irvine n Function constants of all aritys (convention: start with lower case) w mother. Of, times, greater. Than, color n Relation constants, Predicates of all aritys (start with capital) w B 21, Parent, multistoried, XYZ, prime w Terms n n An object constant is a term A function constant of arity n followed by n terms in parenthesis is a term (called functional expression) w mother. Of(Silvia), Sam, leftlegof(John), add 1(5), times(5, plus(3, 6))
 Wffs sentences w An atomic sentence is formed from a predicate (relation) symbol followed by a parenthesized list of symbols n Atoms: a relation constant (predicate) followed by n terms in parenthesis seperated by commas. w Greater. Than(6, 3), Q, Q(A, B, C, D), Brother(Richard, John) w Married(Father. Of(Richard), Mother. Of(John)) w Complex propositional wffs: w Use logic connectives: n n n Brother(Richard, John) / Brother(John, Richard) Older(John, 30) V Younger(John, 30) Older(John) --> ~Younger(John, 30) V P
Wffs sentences w An atomic sentence is formed from a predicate (relation) symbol followed by a parenthesized list of symbols n Atoms: a relation constant (predicate) followed by n terms in parenthesis seperated by commas. w Greater. Than(6, 3), Q, Q(A, B, C, D), Brother(Richard, John) w Married(Father. Of(Richard), Mother. Of(John)) w Complex propositional wffs: w Use logic connectives: n n n Brother(Richard, John) / Brother(John, Richard) Older(John, 30) V Younger(John, 30) Older(John) --> ~Younger(John, 30) V P
 Semantics: Worlds w The world consists of objects that has properties. n n There are relations and functions between these objects Objects in the world, individuals: people, houses, numbers, colors, baseball games, wars, centuries w Clock A, John, 7, the-house in the corner, Tel-Aviv n Functions on individuals: w father-of, best friend, third inning of, one more than n Relations: w brother-of, bigger than, inside, part-of, has color, occurred after n Properties (a relation of arity 1): w red, round, bogus, prime, multistoried, beautiful
Semantics: Worlds w The world consists of objects that has properties. n n There are relations and functions between these objects Objects in the world, individuals: people, houses, numbers, colors, baseball games, wars, centuries w Clock A, John, 7, the-house in the corner, Tel-Aviv n Functions on individuals: w father-of, best friend, third inning of, one more than n Relations: w brother-of, bigger than, inside, part-of, has color, occurred after n Properties (a relation of arity 1): w red, round, bogus, prime, multistoried, beautiful
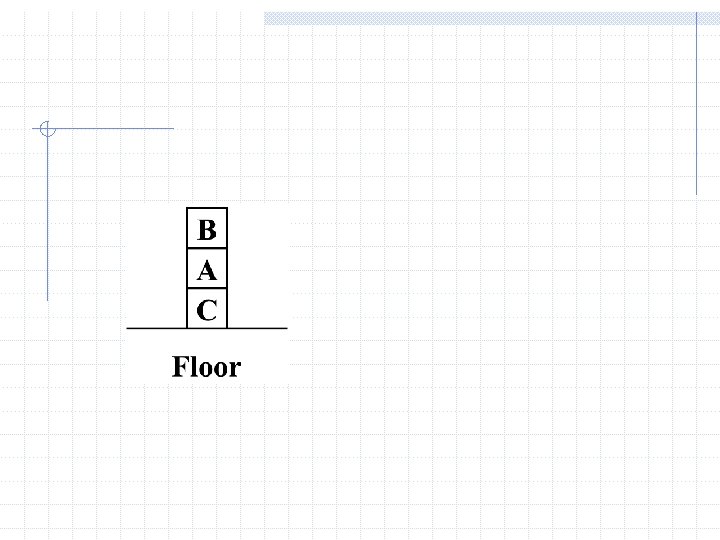
 Semantics: Interpretation w An interpretation of a wff is an assignment that maps n object constants to objects in the worlds, n n-ary function symbols to n-ary functions in the world, n n-ary relation symbols to n-ary relations in the world w Given an interpretation, an atom has the value “true” in case it denotes a relation that holds for those individuals denoted in the terms. Otherwise it has the value “false” n Example: A, B, C, floor, w On, Clear n World: n On(A, B) is false, Clear(B) is true, On(C, F 1) is true…
Semantics: Interpretation w An interpretation of a wff is an assignment that maps n object constants to objects in the worlds, n n-ary function symbols to n-ary functions in the world, n n-ary relation symbols to n-ary relations in the world w Given an interpretation, an atom has the value “true” in case it denotes a relation that holds for those individuals denoted in the terms. Otherwise it has the value “false” n Example: A, B, C, floor, w On, Clear n World: n On(A, B) is false, Clear(B) is true, On(C, F 1) is true…
 Semantics: Models w An interpretation satisfies a wff (sentence) if the wff has the value “true” under the interpretation. w An interpretation that satisfies a wff is a model of that wff w Any wff that has the value “true” under all interpretations is valid w Any wff that does not have a model is inconsistent or unsatisfiable w If a wff w has a value true under all the models of a set of sentences delta then delta logically entails w
Semantics: Models w An interpretation satisfies a wff (sentence) if the wff has the value “true” under the interpretation. w An interpretation that satisfies a wff is a model of that wff w Any wff that has the value “true” under all interpretations is valid w Any wff that does not have a model is inconsistent or unsatisfiable w If a wff w has a value true under all the models of a set of sentences delta then delta logically entails w
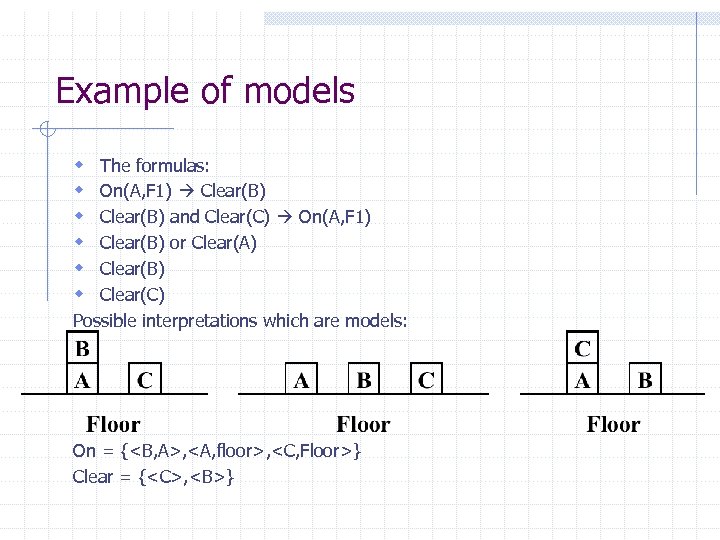 Example of models w w w The formulas: On(A, F 1) Clear(B) and Clear(C) On(A, F 1) Clear(B) or Clear(A) Clear(B) Clear(C) Possible interpretations which are models: On = {
Example of models w w w The formulas: On(A, F 1) Clear(B) and Clear(C) On(A, F 1) Clear(B) or Clear(A) Clear(B) Clear(C) Possible interpretations which are models: On = {
 Quantification w Universal and existential quantifiers allow expressing general rules with variables w Universal quantification n All cats are mammals w n It is equivalent to the conjunction of all the sentences obtained by substitution the name of an object for the variable x. w Syntax: if w is a wff then (forall x) w is a wff.
Quantification w Universal and existential quantifiers allow expressing general rules with variables w Universal quantification n All cats are mammals w n It is equivalent to the conjunction of all the sentences obtained by substitution the name of an object for the variable x. w Syntax: if w is a wff then (forall x) w is a wff.
 Quantification: Existential w Existential quantification : an existentially quantified sentence is true in case one of the disjunct is true w Equivalent to disjunction: w We can mix existential and universal quantification.
Quantification: Existential w Existential quantification : an existentially quantified sentence is true in case one of the disjunct is true w Equivalent to disjunction: w We can mix existential and universal quantification.
 Useful Equivalences w De Morgan laws w Inference rules: n Universal instantiation: foall x f(x) |-- f(alpha) n Existential generalization: from f(alpha) |-- exist x f(x)
Useful Equivalences w De Morgan laws w Inference rules: n Universal instantiation: foall x f(x) |-- f(alpha) n Existential generalization: from f(alpha) |-- exist x f(x)
 Modeling a domain; Conceptualization w The kinship domain: n n object are people Properties include gender and they are related by relations such as parenthood, brotherhood, marriage n predicates: Male, Female (unary) Parent, Sibling, Daughter, Son. . . n Function: Mother Father
Modeling a domain; Conceptualization w The kinship domain: n n object are people Properties include gender and they are related by relations such as parenthood, brotherhood, marriage n predicates: Male, Female (unary) Parent, Sibling, Daughter, Son. . . n Function: Mother Father
 Resolution in the predicate calculus w Unification n w w w Algorithm unify Using unification in predicate calculus resolution Completeness and soundness Converting a wff to clause form The mechanics of resolution Answer extraction
Resolution in the predicate calculus w Unification n w w w Algorithm unify Using unification in predicate calculus resolution Completeness and soundness Converting a wff to clause form The mechanics of resolution Answer extraction
 Inference Rules in FOL w All the inference rules for propositional logic applies and additional three rules that use substitution; assigning constants to variables n Subst(x/constant) n Subst({x/Sam, y/Pam}, Likes(x, y)) = Likes(Sam, Pam) w Universal elimination n From fromall x Likes(x, Ice. Cream) we can substitute {x/Ben} and infer Likes(Ben, Ice. Cream) w Existential Elimination n For any sentence and for any symbol k that does not appear elsewhere in the knowledge-base w exists x Kill(x, Victim) we can infer Kill(Murderer, victim) n As long as Murdered soes not appear anywhere w Existential introduction n From Likes(Jerry, Ice. Cream) we can infer exists x Likes(x, Ice. Cream)
Inference Rules in FOL w All the inference rules for propositional logic applies and additional three rules that use substitution; assigning constants to variables n Subst(x/constant) n Subst({x/Sam, y/Pam}, Likes(x, y)) = Likes(Sam, Pam) w Universal elimination n From fromall x Likes(x, Ice. Cream) we can substitute {x/Ben} and infer Likes(Ben, Ice. Cream) w Existential Elimination n For any sentence and for any symbol k that does not appear elsewhere in the knowledge-base w exists x Kill(x, Victim) we can infer Kill(Murderer, victim) n As long as Murdered soes not appear anywhere w Existential introduction n From Likes(Jerry, Ice. Cream) we can infer exists x Likes(x, Ice. Cream)
 Predicate calculus resolution w Suppose the 1 and 2 are two clauses represented as set of literals. If there is an atom in 1 and a literal ~ in 2 such as and have a common unifier w Then these two clauses have a resolvent row. It is obtained by applying the substitution to 1 2 leaving out complementary literals w Example:
Predicate calculus resolution w Suppose the 1 and 2 are two clauses represented as set of literals. If there is an atom in 1 and a literal ~ in 2 such as and have a common unifier w Then these two clauses have a resolvent row. It is obtained by applying the substitution to 1 2 leaving out complementary literals w Example:
 Converting to clause form
Converting to clause form
 Example: Answer Extraction
Example: Answer Extraction
 Example: Resoluction Refutation Prove I(A, 27)
Example: Resoluction Refutation Prove I(A, 27)
 Rule-Based Systems w Rule-based Knowledge Representation and Inference n combines rules w if DOG(x) then TAIL(X) n with working memory, w DOG(SPOT) w DOG(LUNA) n is not a formal knowledge representation scheme like logic w somewhat like a combination of propositional and FOPL w uses simple methods for inference w often combined with other mechanisms such as inheritance w motivated by practical use rather than theoretical properties w also has some basis in cognitive models
Rule-Based Systems w Rule-based Knowledge Representation and Inference n combines rules w if DOG(x) then TAIL(X) n with working memory, w DOG(SPOT) w DOG(LUNA) n is not a formal knowledge representation scheme like logic w somewhat like a combination of propositional and FOPL w uses simple methods for inference w often combined with other mechanisms such as inheritance w motivated by practical use rather than theoretical properties w also has some basis in cognitive models
 Forward Chaining Procedure While (rules can still fire or goal is not reached) for each rule in the rulebase which has not fired 1. try to bind premises by matching to assertions in WM 2. if all premises in a rule are supported then assert the conclusion and add to WM Repeat 1. and 2. for all matching/ instantiation alternatives end continue
Forward Chaining Procedure While (rules can still fire or goal is not reached) for each rule in the rulebase which has not fired 1. try to bind premises by matching to assertions in WM 2. if all premises in a rule are supported then assert the conclusion and add to WM Repeat 1. and 2. for all matching/ instantiation alternatives end continue
 Example: Zoo Rulebase w Want to identify animals based on their characteristics w could have rules like n if A 1 and A 2 and A 3. . . and A 27 then animal is a monkey n i. e. , one very specific rule per animal w Better to use intermediate concepts n e. g. , the intermediate concept of a mammal n if ? x is a mammal and B 1. . . and B 3 then ? x is a monkey w Why are intermediate concepts useful? n rules are easier to create n rulebase is easier to maintain n easier to perform inference
Example: Zoo Rulebase w Want to identify animals based on their characteristics w could have rules like n if A 1 and A 2 and A 3. . . and A 27 then animal is a monkey n i. e. , one very specific rule per animal w Better to use intermediate concepts n e. g. , the intermediate concept of a mammal n if ? x is a mammal and B 1. . . and B 3 then ? x is a monkey w Why are intermediate concepts useful? n rules are easier to create n rulebase is easier to maintain n easier to perform inference
 Where do the rules come from ? w Manual Knowledge Acquisition n interview experts n expert describes the rules n n process of translating expert knowledge into a formal representation is also known as knowledge engineering this is notoriously difficult w experts are often very poor at explicitly describing what they do w e. g. , ask Michael Jordan how he plays basketball or ask Tiger Woods how he plays golf w Automated Knowledge Acquisition n derive rules automatically from formal specifications w e. g. , by automatic analysis of solution manuals n machine learning
Where do the rules come from ? w Manual Knowledge Acquisition n interview experts n expert describes the rules n n process of translating expert knowledge into a formal representation is also known as knowledge engineering this is notoriously difficult w experts are often very poor at explicitly describing what they do w e. g. , ask Michael Jordan how he plays basketball or ask Tiger Woods how he plays golf w Automated Knowledge Acquisition n derive rules automatically from formal specifications w e. g. , by automatic analysis of solution manuals n machine learning
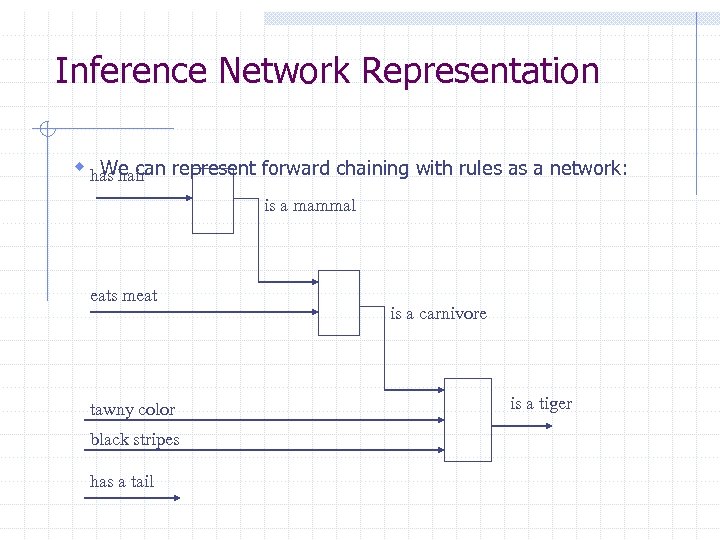 Inference Network Representation w has hair represent forward chaining with rules as a network: We can is a mammal eats meat tawny color black stripes has a tail is a carnivore is a tiger
Inference Network Representation w has hair represent forward chaining with rules as a network: We can is a mammal eats meat tawny color black stripes has a tail is a carnivore is a tiger
 Inference using Backward Chaining w Establish a hypothesis n e. g. , Tony is a tiger n a hypothesis is as assertion whose truth we wish to test w i. e. , assert the hypothesis w see if that is consistent with other data w Work backwards, i. e. , n match the hypothesis to the conclusion of the rules n look at the premise conditions of the rule w if these are unknown, n declare these as intermediate hypotheses n backward chain recursively (depth-first manner) w Can use search algorithms to control how backward chaining proceeds
Inference using Backward Chaining w Establish a hypothesis n e. g. , Tony is a tiger n a hypothesis is as assertion whose truth we wish to test w i. e. , assert the hypothesis w see if that is consistent with other data w Work backwards, i. e. , n match the hypothesis to the conclusion of the rules n look at the premise conditions of the rule w if these are unknown, n declare these as intermediate hypotheses n backward chain recursively (depth-first manner) w Can use search algorithms to control how backward chaining proceeds
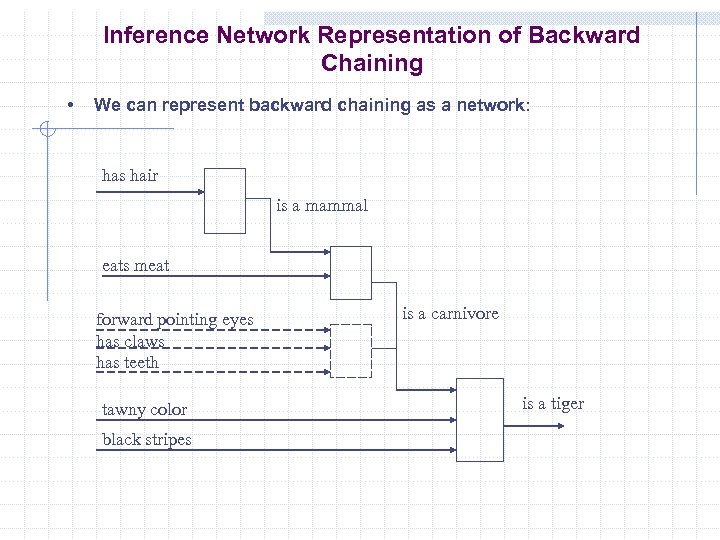 Inference Network Representation of Backward Chaining • We can represent backward chaining as a network: has hair is a mammal eats meat forward pointing eyes has claws has teeth tawny color black stripes is a carnivore is a tiger
Inference Network Representation of Backward Chaining • We can represent backward chaining as a network: has hair is a mammal eats meat forward pointing eyes has claws has teeth tawny color black stripes is a carnivore is a tiger
 Backward Chaining Procedure While (unsupported hypotheses exist or goal is not reached) for each hypothesis H for each rule R whose conclusion matches with H try to support each rule’s premises by 1. matching assertions in WM 2. recursively applying backward chaining if rule’s premises are supported conclude that H is true end continue
Backward Chaining Procedure While (unsupported hypotheses exist or goal is not reached) for each hypothesis H for each rule R whose conclusion matches with H try to support each rule’s premises by 1. matching assertions in WM 2. recursively applying backward chaining if rule’s premises are supported conclude that H is true end continue
 Forward Chaining or Backward Chaining: which is better? w Which direction is better depends on the circumstances w 4 main factors of relevance n the number of possible start states and number of possible goal states w smaller is better n the branching factor in each direction w smaller is better n what type of explanation the user wants w more natural explanations may be important n the typical action which triggers a rule w i. e. , data-driven or hypothesis-driven?
Forward Chaining or Backward Chaining: which is better? w Which direction is better depends on the circumstances w 4 main factors of relevance n the number of possible start states and number of possible goal states w smaller is better n the branching factor in each direction w smaller is better n what type of explanation the user wants w more natural explanations may be important n the typical action which triggers a rule w i. e. , data-driven or hypothesis-driven?
 What is a rule-based expert system (ES)? w ES performs a task in limited domains that require human expertise n medical diagnosis; fault diagnosis; status monitoring; data interpretation; mineral exploration; credit checking; tutoring; computer configuration w ES solves problems by application of domain specific knowledge rather than weak methods. w Domain knowledge is acquired by interviewing human experts w ES can explain a problem solution in human-understandable terms
What is a rule-based expert system (ES)? w ES performs a task in limited domains that require human expertise n medical diagnosis; fault diagnosis; status monitoring; data interpretation; mineral exploration; credit checking; tutoring; computer configuration w ES solves problems by application of domain specific knowledge rather than weak methods. w Domain knowledge is acquired by interviewing human experts w ES can explain a problem solution in human-understandable terms
 Examples of Expert Systems 1965 1972 1975 1978 1979 1980 1982 1983 1984 1986 1987 1992 1995 1997 DENDRAL MACSYMA MYCIN Prospector Cadeceus DIGITALIS PUFF R 1 XCON KNOBS ACE FAITH ACES DELTA/CATS MAX Stanford MIT Stanford SRI analyze mass spectrometry data symbolic mathematics problems diagnosis of blood diseases Mineral Exploration U. of PITT Internal Medicine MIT digitalis therapy advise Stanford obstructive airway diseases CMU computer configuration DEC computer configuration MITRE mission planning AT&T diagnosis faults in telephone cables JPL spacecraft diagnosis Aerospace satellite anomaly diagnosis Cambpell diagnose cooker malfunctions GE diagnosis of diesel locomotives AMEX credit authorization NYNEX telephone network troubleshooting Caltech Pac. Bell network management UCI planning drug treatment for HIV
Examples of Expert Systems 1965 1972 1975 1978 1979 1980 1982 1983 1984 1986 1987 1992 1995 1997 DENDRAL MACSYMA MYCIN Prospector Cadeceus DIGITALIS PUFF R 1 XCON KNOBS ACE FAITH ACES DELTA/CATS MAX Stanford MIT Stanford SRI analyze mass spectrometry data symbolic mathematics problems diagnosis of blood diseases Mineral Exploration U. of PITT Internal Medicine MIT digitalis therapy advise Stanford obstructive airway diseases CMU computer configuration DEC computer configuration MITRE mission planning AT&T diagnosis faults in telephone cables JPL spacecraft diagnosis Aerospace satellite anomaly diagnosis Cambpell diagnose cooker malfunctions GE diagnosis of diesel locomotives AMEX credit authorization NYNEX telephone network troubleshooting Caltech Pac. Bell network management UCI planning drug treatment for HIV
 Mycin: Diagnosis and treatment of blood diseases RULES PREMISE ($AND (SAME CNTXT GRAMNEG) (SAME CNTXT MORH ROD) (SAME CNTXT AIR AEROBIC)) ACTION: (CONCLUDE CNTXT CLASS ENTEROBACTERIACEAE. 8) If THEN the stain of the organism is gramneg, and the morphology of the organism is rod, and the aerobicity of the organism is aerobic there is strongly suggestive evidence (. 8) that the class of organism is enterocabateriaceae DATA ORGANISM-1: GRAM = (GRAMNEG 1. 0) MORP = (ROD. 8) (COCCUS. 2) AIR = (AEROBIC. 6)(FACUL. 4)
Mycin: Diagnosis and treatment of blood diseases RULES PREMISE ($AND (SAME CNTXT GRAMNEG) (SAME CNTXT MORH ROD) (SAME CNTXT AIR AEROBIC)) ACTION: (CONCLUDE CNTXT CLASS ENTEROBACTERIACEAE. 8) If THEN the stain of the organism is gramneg, and the morphology of the organism is rod, and the aerobicity of the organism is aerobic there is strongly suggestive evidence (. 8) that the class of organism is enterocabateriaceae DATA ORGANISM-1: GRAM = (GRAMNEG 1. 0) MORP = (ROD. 8) (COCCUS. 2) AIR = (AEROBIC. 6)(FACUL. 4)
 The XCON Application w A rule-based expert system n expert in the sense that the rules capture expert design knowledge n addresses a design/configuration problem w Digital Equipment Corporation (or Compaq by now!) n XCON = rule-based expert system for computer configuration n decides how peripherals are configured on new orders n has 10, 000 rules n developed in early 1980’s n based on “reactive rule-based systems” w if antecedents then action w forward chaining in style n estimated to have saved DEC several hundred million $’s
The XCON Application w A rule-based expert system n expert in the sense that the rules capture expert design knowledge n addresses a design/configuration problem w Digital Equipment Corporation (or Compaq by now!) n XCON = rule-based expert system for computer configuration n decides how peripherals are configured on new orders n has 10, 000 rules n developed in early 1980’s n based on “reactive rule-based systems” w if antecedents then action w forward chaining in style n estimated to have saved DEC several hundred million $’s
 Limitations of Rule-Based Representations w Can be difficult to create n the “knowledge engineering” problem w Can be difficult to maintain n in large rule-bases, adding a rule can cause many unforeseen interactions and effects => difficult to debug w Many types of knowledge are not easily represented by rules n uncertain knowledge: “if it is cold it will probably rain” n information which changes over time n procedural information (e. g. a sequence of tests to diagnose a disease)
Limitations of Rule-Based Representations w Can be difficult to create n the “knowledge engineering” problem w Can be difficult to maintain n in large rule-bases, adding a rule can cause many unforeseen interactions and effects => difficult to debug w Many types of knowledge are not easily represented by rules n uncertain knowledge: “if it is cold it will probably rain” n information which changes over time n procedural information (e. g. a sequence of tests to diagnose a disease)
 Summary w Knowledge Representation methods n formal logic n rule-based systems (less formal) w Rule-based representations are composed of n Working memory: n Rules w Inference occurs by n forward or backward chaining w Rule-based expert systems n useful for certain classes of problems which do not have direct algorithmic solutions
Summary w Knowledge Representation methods n formal logic n rule-based systems (less formal) w Rule-based representations are composed of n Working memory: n Rules w Inference occurs by n forward or backward chaining w Rule-based expert systems n useful for certain classes of problems which do not have direct algorithmic solutions


