Нормальным вектором плоскости или нормалью плоскости называют вектор

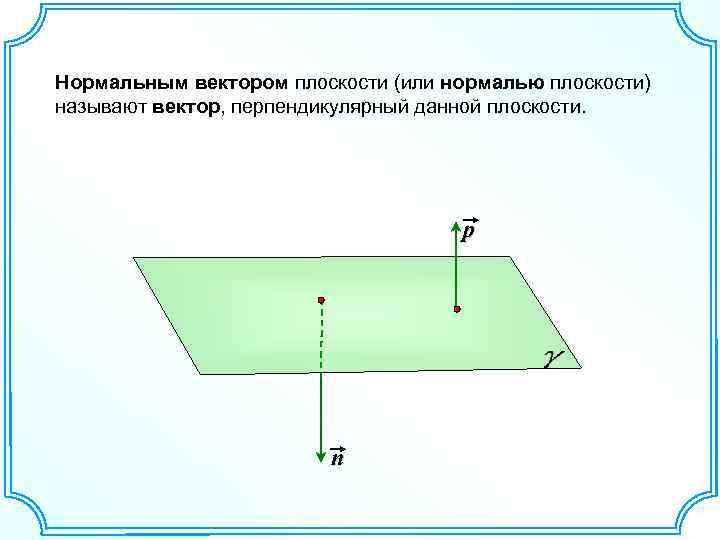Нормальным вектором плоскости (или нормалью плоскости) называют вектор, перпендикулярный данной плоскости. p n

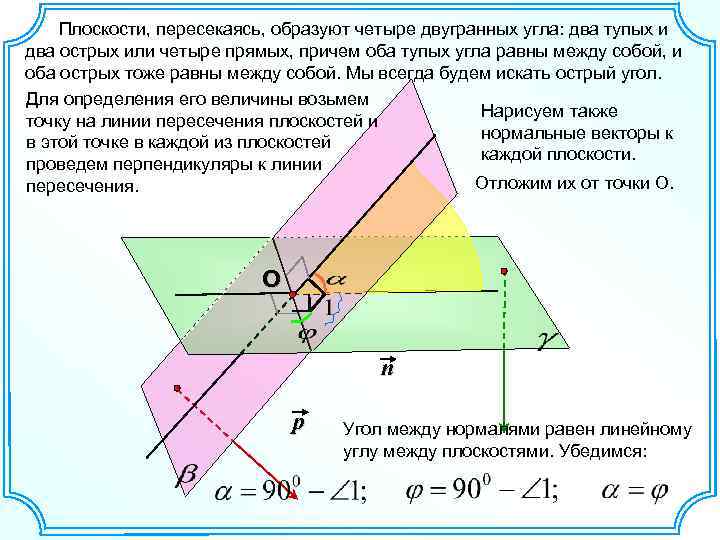Плоскости, пересекаясь, образуют четыре двугранных угла: два тупых и два острых или четыре прямых, причем оба тупых угла равны между собой, и оба острых тоже равны между собой. Мы всегда будем искать острый угол. Для определения его величины возьмем Нарисуем также точку на линии пересечения плоскостей и нормальные векторы к в этой точке в каждой из плоскостей каждой плоскости. проведем перпендикуляры к линии Отложим их от точки О. пересечения. О n p Угол между нормалями равен линейному углу между плоскостями. Убедимся:

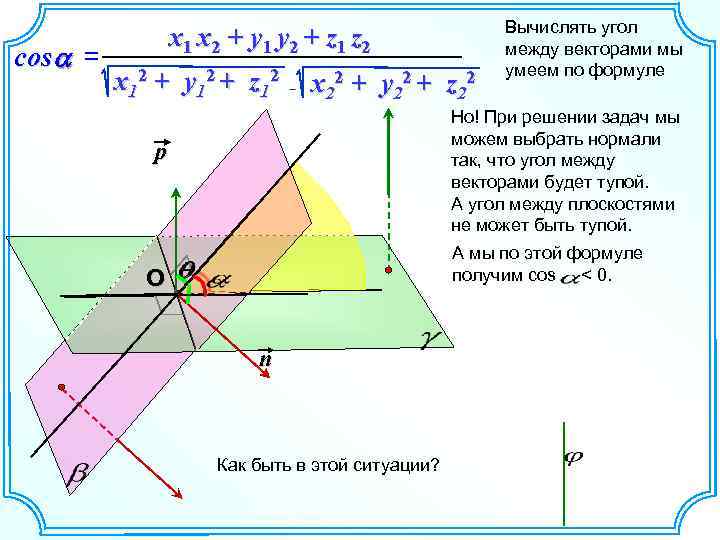cos a = x 1 x 2 + y 1 y 2 + z 1 z 2 x 12 + y 12 + z 12 x 22 + y 22 + z 22 Вычислять угол между векторами мы умеем по формуле Но! При решении задач мы можем выбрать нормали так, что угол между векторами будет тупой. А угол между плоскостями не может быть тупой. p А мы по этой формуле получим cos < 0. О n Как быть в этой ситуации?

a - искомый угол между прямой и плоскостью q - угол между векторами p и n p (уже обосновали) n Тогда cos a = x 1 x 2 + y 1 y 2 + z 1 z 2 x 12 + y 12 + z 12 x 22 + y 22 + z 22 Итак, если угол между нормалями острый, то мы сразу получаем угол между плоскостями (формула со знаком «+» ). Если угол между нормалями тупой, то чтобы получить косинус острого угла, надо взять полученный косинус со знаком «–» . А лучше и проще…

Алгоритм. Применение скалярного произведения для вычисления угла между плоскостями. 1. Нормальный вектор (нормаль) для первой плоскости 2. Нормальный вектор (нормаль) для второй плоскости 3. Вычислить cos a по формуле cos a = x 1 x 2 + y 1 y 2 + z 1 z 2 x 12 + y 12 + z 12 x 22 + y 22 + z 22 4. Найти угол a. Если значение косинуса не табличное, то записать ответ, используя арккосинус. Данная формула даст правильный ответ (острый угол между прямыми), даже если вы при решении задачи выберите нормальные векторы так, что угол между ними будет тупой.

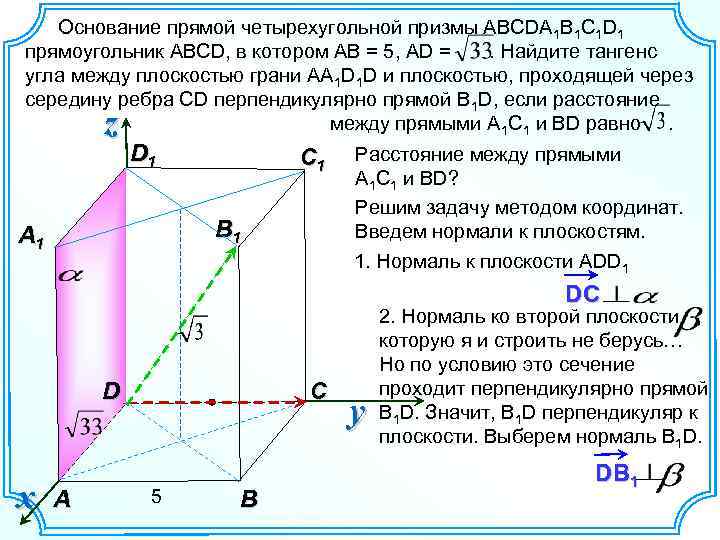Основание прямой четырехугольной призмы ABCDA 1 B 1 C 1 D 1 прямоугольник ABCD, в котором AB = 5, AD =. Найдите тангенс угла между плоскостью грани AA 1 D 1 D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B 1 D, если расстояние между прямыми A 1 C 1 и BD равно. z D 1 C 1 B 1 A 1 Расстояние между прямыми A 1 C 1 и BD? Решим задачу методом координат. Введем нормали к плоскостям. 1. Нормаль к плоскости АDD 1 DC D x A C 5 B y 2. Нормаль ко второй плоскости , которую я и строить не берусь… Но по условию это сечение проходит перпендикулярно прямой В 1 D. Значит, В 1 D перпендикуляр к плоскости. Выберем нормаль B 1 D. DB 1

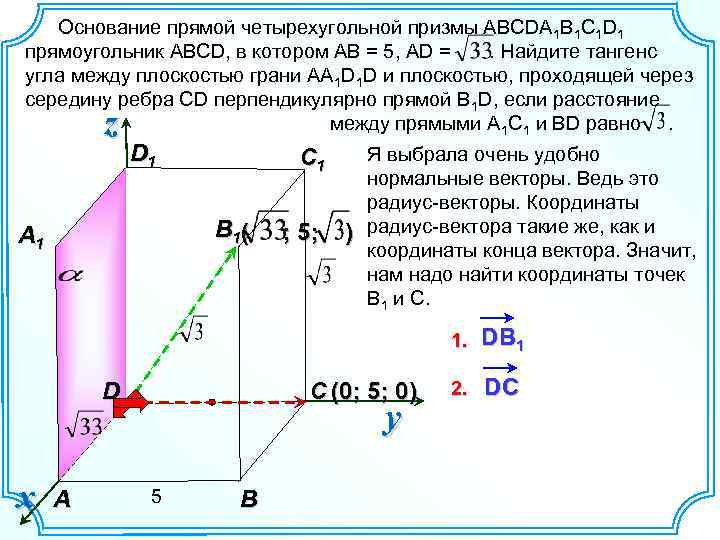Основание прямой четырехугольной призмы ABCDA 1 B 1 C 1 D 1 прямоугольник ABCD, в котором AB = 5, AD =. Найдите тангенс угла между плоскостью грани AA 1 D 1 D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B 1 D, если расстояние между прямыми A 1 C 1 и BD равно. z D 1 C 1 B 1 ( A 1 ; 5; ) Я выбрала очень удобно нормальные векторы. Ведь это радиус-векторы. Координаты радиус-вектора такие же, как и координаты конца вектора. Значит, нам надо найти координаты точек В 1 и С. 1. D x A C (0; 5; 0) y 5 B DB 1 2. DC

DB 1 ( 3. ; 5; ) DC (0; 5; 0) Теперь найдем тангенс. 2 tg A + 1 = т. к. 1 cos 2 A – острый угол

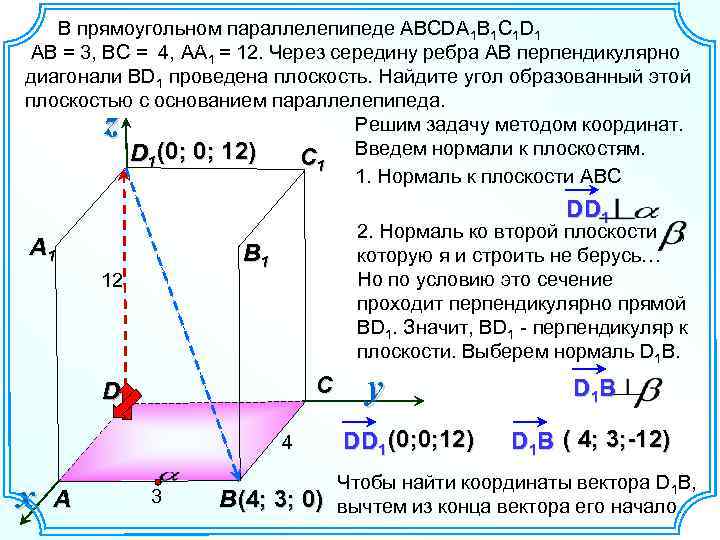В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 AB = 3, ВС = 4, АА 1 = 12. Через середину ребра АВ перпендикулярно диагонали ВD 1 проведена плоскость. Найдите угол образованный этой плоскостью с основанием параллелепипеда. Решим задачу методом координат. D 1 (0; 0; 12) C 1 Введем нормали к плоскостям. 1. Нормаль к плоскости АBC z DD 1 A 1 2. Нормаль ко второй плоскости , которую я и строить не берусь… Но по условию это сечение проходит перпендикулярно прямой BD 1. Значит, ВD 1 - перпендикуляр к плоскости. Выберем нормаль D 1 B. B 1 12 C D 4 x A 3 B (4 ; 3 ; 0 ) y DD 1 (0; 0; 12) D 1 B ( 4; 3; -12) DD 1 – это радиус-вектор, поэтому 1 B, Чтобы найти координаты вектора Dего координаты такие же, как и начало. вычтем из конца вектора его точки D 1

DD 1 (0; 0; 12) D 1 B ( 4; 3; -12) 12

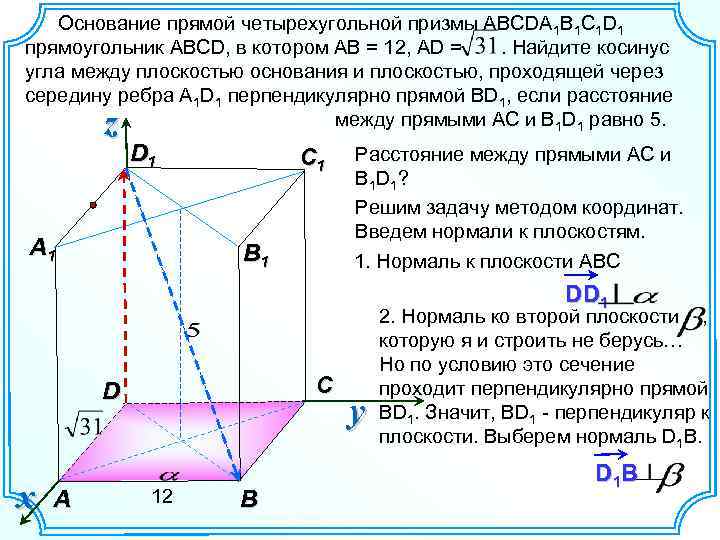Основание прямой четырехугольной призмы ABCDA 1 B 1 C 1 D 1 прямоугольник ABCD, в котором AB = 12, AD =. Найдите косинус угла между плоскостью основания и плоскостью, проходящей через середину ребра A 1 D 1 перпендикулярно прямой BD 1, если расстояние между прямыми AC и B 1 D 1 равно 5. z D 1 A 1 C 1 B 1 Расстояние между прямыми AC и B 1 D 1 ? Решим задачу методом координат. Введем нормали к плоскостям. 1. Нормаль к плоскости АBC DD 1 C D x A 12 B y 2. Нормаль ко второй плоскости , которую я и строить не берусь… Но по условию это сечение проходит перпендикулярно прямой BD 1. Значит, ВD 1 - перпендикуляр к плоскости. Выберем нормаль D 1 B

Основание прямой четырехугольной призмы ABCDA 1 B 1 C 1 D 1 прямоугольник ABCD, в котором AB = 12, AD =. Найдите косинус угла между плоскостью основания и плоскостью, проходящей через середину ребра A 1 D 1 перпендикулярно прямой BD 1, если расстояние между прямыми AC и B 1 D 1 равно 5. D 1 (0; 0; 5) C 1 DD 1 – это радиус-вектор, поэтому его координаты такие же, как и точки D 1 z DD 1 (0; 0; 5) A 1 B 1 Чтобы найти координаты вектора D 1 B, 5 вычтем из конца вектора его начало. D 1 B ( C D x A 12 B( y ; 12; 0) ; 12; -5)

DD 1 (0; 0; 5) D 1 B ( ; 12; -5)

В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 известны ребра: , AB = 5, AD = 12, СС 1 = 5. Найдите угол между плоскостями CD 1 B 1 и AD 1 B 1. В данной задаче построение линейного угла не столь очевидно. z Поэтому применим метод координат. D 1 (0 ; 5 ) C 1 Найдем вектор нормали плоскости AD 1 B 1. Из (1): Рассмотрим два вектора этой плоскости: «–» A 1 5 AD 1 (-12; 0; 5) B 1 (12; 5; 5) AB 1 (0; 5; 5) Пусть вектор нормали n {x; y; z}. Вектор, перпендикулярный плоскости, будет перпендикулярен D 5 C (0; 5; 0) любой прямой, лежащей в этой Эта система имеет бесконечное плоскости. Тогда, y множество решений, так как 12 AD 1 n значит, AD 1 n = 0 векторов, перпендикулярных 5 AB 1 n значит, AB 1 n = 0 плоскости )AD 1 B 1, бесконечно A (12; 0; 0 B х много. Выберем из данного множества ненулевой вектор n, положив х = 1, 12 тогда у = – , z = 12 5 5 Получим систему Вектор нормали плоскости AD 1 B 1: n (1; – 12; 12 ) 5 5

В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 известны ребра: , AB = 5, AD = 12, СС 1 = 5. Найдите угол между плоскостями CD 1 B 1 и AD 1 B 1. z D 1 (0 ; 5 ) C 1 Найдем вектор нормали плоскости CD 1 B 1. Из (2): Рассмотрим два вектора этой плоскости: «–» A 1 5 CD 1 (0; -5; 5) B 1 (12; 5; 5) CB 1 (12; 0; 5) Пусть вектор нормали s {x; y; z}. Вектор, перпендикулярный плоскости, будет перпендикулярен D 5 C (0; 5; 0) любой прямой, лежащей в этой плоскости. Тогда, Эта система имеет бесконечное y 1 решений, так как множество 2 CD 1 s значит, CD 1 s = 0 векторов, перпендикулярных 5 CB 1 s значит, CB 1 s = 0 плоскости 0) 1 B 1, бесконечно CD A (12; 0; B х много. Выберем из данного множества ненулевой вектор s, положив х = 1, тогда у = – 12 , z = – 12 5 5 Получим систему Вектор нормали плоскости CD 1 B 1: s (1; – 12) 5 5

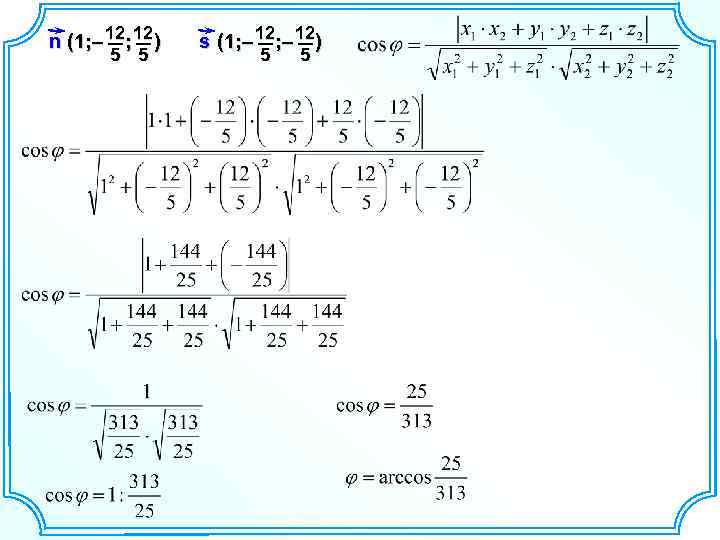n (1; – 12; 12 ) 5 5 s (1; – 12) 5 5

Дан прямоугольный параллелепипед ABCDA 1 B 1 C 1 D 1, длины ребер которого АВ = 2, AD = AA 1 = 1. Найдите угол между плоскостями CD 1 B 1 и CDA 1. Радиус-вектор имеет такие же координаты, как и его конец. z CD (0; 2; 0) C 1 D 1 CB 1 (1; 0; 1) Найдем вектор нормали плоскости СDА 1. A 1 Пусть вектор нормали n {x; y; z}. 1 Вектор, перпендикулярный Эта система имеет бесконечное плоскости, будет перпендикулярен множество решений, так как 1 векторов, перпендикулярных любой прямой, лежащей в этой плоскости СDА 1, бесконечно плоскости. Тогда, много. Выберем из данного CD n значит, CD n = 0 множества ненулевой вектор n, D (0; 2; 0) C положив х = 1, 2 CB 1 n значит, CB 1 n = 0 y 1 у=0 , z=– 1 тогда Получим плоскости 1 Вектор нормали систему СDА 1: B 1 (1 ; 0 ; 1 ) х B 2 A n (1; 0; – 1)

Дан прямоугольный параллелепипед ABCDA 1 B 1 C 1 D 1, длины ребер которого АВ = 2, AD = AA 1 = 1. Найдите угол между плоскостями CD 1 B 1 и CDA 1. Радиус-вектор имеет такие же координаты, как и его конец. z CD 1 (0; 2; 1) C Из (2) 1 «–» Найдем вектор нормали плоскости СD 1 В 1. B 1 (1 ; 0 ; 1 ) A 1 1 1 Эта система имеет бесконечное множество решений, так как векторов, перпендикулярных плоскости СD 1 B 1, бесконечно много. Выберем из данного множества ненулевой вектор s. D (0; 2; 0) , 2 C y положив х = 2, 1 тогда у = 1 х B CB 1 (1; 0; 1) D 1 (0; 2; 1) 1 , z=– 2 2 A Пусть вектор нормали s {x; y; z}. Вектор, перпендикулярный плоскости, будет перпендикулярен любой прямой, лежащей в этой плоскости. Тогда, CD 1 s значит, CD 1 s = 0 CB 1 s значит, CB 1 s = 0 Получим плоскости СD 1 А 1: Вектор нормали систему s (2; 1; – 2)

n (1; 0; – 1) 2 s (2; 1; – 2)

В правильной четырехугольной призме ABCDA 1 B 1 C 1 D 1 диагональ основания в 2 раза больше бокового ребра. Найдите угол между плоскостью АCB 1 и боковой гранью ВВ 1 С 1 С. В данной задаче построение линейного угла не столь очевидно. Поэтому применим метод координат. Если в задаче не дано числовое Вектор нормали плоскости ВВ 1 С 1: значение, то можем обозначить / : 2 Из (1) боковое ребро плоскости АCB 1. Найдем вектор нормали « 1» , тогда диагональ z основания равна 2. Найдем сторону Рассмотрим два вектора этой плоскости: D 1 основания. Основание – квадрат. C 1 С D AC (- 2 ; 0) AB 1 (0; 2 ; 1) Пусть вектор нормали n {x; y; z}. 2 ? A 1 B 1 ( 2 ; 1 ) Вектор, перпендикулярный Эта система имеет бесконечное плоскости, будет перпендикулярен 450 А множество решений, так как любой прямой, В лежащей в этой векторов, перпендикулярных плоскости. Тогда, 2 D плоскости ACB 1, бесконечно C (0 ; 2 ; 0 ) p (0; 2 ; 0) AC n значит, AC n = 0 много. Выберем из данного y 2 множества ненулевой вектор n, AB 1 n значит, AB 1 n = 0 1 х A ( 2; 0; 0) положив х = 1, тогда у. B 1, z = – 2 = Получим систему Вектор нормали плоскости ACB 1: n (1; 1; - 2)

p (0; 2 ; 0) n (1; 1; - 2)

В правильной четырехугольной призме АВСDA 1 B 1 C 1 D 1 стороны основания равны 2, а боковые ребра равны 5. На ребре АА 1 отмечена точка Е так, что АЕ : ЕА 1 = 3 : 2. Найдите угол между плоскостями АВС AA 1 = 5, это – 5 частей, тогда и ВЕD 1. = 3 Вектор нормали плоскости АВС: s (0; 0; 1) АЕ = 5: 5*3 ЕА 1= 5: 5*2 = 2 z D 1(0; 0; 5) D 1 F (0; 2; -3) C 1 D 1 E (2; 0; -2) 3 части 2 части Найдем вектор нормали плоскости ВЕD 1. A 1 3 B 1 Пусть вектор нормали n {x; y; z}. Вектор, перпендикулярный 2 плоскости, будет перпендикулярен Эта система имеет бесконечное F (0; 2; 2) любой прямой, лежащей в этой множество решений, так как E 5 (2; 0; перпендикулярных векторов, 3) плоскости. Тогда, плоскости BED 1, бесконечно 2 D 1 F n значит, D 1 F n = 0 много. Выберем из данного 3 D 1 E n значит, D 1 E n = 0 множества ненулевой вектор n, C D y положив х = 2, 2 Вектор нормали Получим систему1: n (2; 3; 2) плоскости ВЕD тогда у = 3, z = 2 х А 2 В

s (0; 0; 1) n (2; 3; 2)