Нормальные формы отношений Этапы























Лекция 9. Нормализация.ppt
- Количество слайдов: 24
 Нормальные формы отношений Этапы разработки базы данных При разработке базы данных обычно выделяется несколько уровней моделирования, при помощи которых происходит переход от предметной области к конкретной реализации базы данных средствами конкретной СУБД. Можно выделить следующие уровни: • Сама предметная область • Модель предметной области • Логическая модель данных • Физическая модель данных • Собственно база данных и приложения
Нормальные формы отношений Этапы разработки базы данных При разработке базы данных обычно выделяется несколько уровней моделирования, при помощи которых происходит переход от предметной области к конкретной реализации базы данных средствами конкретной СУБД. Можно выделить следующие уровни: • Сама предметная область • Модель предметной области • Логическая модель данных • Физическая модель данных • Собственно база данных и приложения
 Нормальные формы отношений Нормализация Для правильного проектирования модели данных применяется метод нормализации отношений. Нормализация представляет собой процесс реорганизации данных путем ликви дации повторяющихся групп и иных противоречий с целью приведения таблиц к виду, позволяющему осуществлять непротиворечивое и корректное редактиро вание данных.
Нормальные формы отношений Нормализация Для правильного проектирования модели данных применяется метод нормализации отношений. Нормализация представляет собой процесс реорганизации данных путем ликви дации повторяющихся групп и иных противоречий с целью приведения таблиц к виду, позволяющему осуществлять непротиворечивое и корректное редактиро вание данных.
 Нормальные формы отношений Цели нормализации Обычно различают следующие проблемы, возникающие при наличии ненормализованных таблиц: • избыточность данных; • аномалии обновления; • аномалии удаления; • аномалии ввода.
Нормальные формы отношений Цели нормализации Обычно различают следующие проблемы, возникающие при наличии ненормализованных таблиц: • избыточность данных; • аномалии обновления; • аномалии удаления; • аномалии ввода.
 Нормальные формы отношений Пример Рассмотрим в качестве предметной области некоторую организацию, выполняющую некоторые проекты. Сотрудники организации выполняют проекты. Проекты состоят из нескольких заданий. Каждый сотрудник может участвовать в одном или нескольких проектах, или временно не участвовать ни в каких проектах. Над каждым проектом может работать несколько сотрудников, или временно проект может быть приостановлен, тогда над ним не работает ни один сотрудник. Над каждым заданием в проекте работает ровно один сотрудник. Каждый сотрудник числится в одном отделе. Каждый сотрудник имеет телефон, находящийся в отделе сотрудника.
Нормальные формы отношений Пример Рассмотрим в качестве предметной области некоторую организацию, выполняющую некоторые проекты. Сотрудники организации выполняют проекты. Проекты состоят из нескольких заданий. Каждый сотрудник может участвовать в одном или нескольких проектах, или временно не участвовать ни в каких проектах. Над каждым проектом может работать несколько сотрудников, или временно проект может быть приостановлен, тогда над ним не работает ни один сотрудник. Над каждым заданием в проекте работает ровно один сотрудник. Каждый сотрудник числится в одном отделе. Каждый сотрудник имеет телефон, находящийся в отделе сотрудника.
 Нормальные формы отношений Пример В ходе дополнительного уточнения того, какие данные необходимо учитывать, выяснилось следующее: О каждом сотруднике необходимо хранить табельный номер и фамилию. Табельный номер является уникальным для каждого сотрудника. Каждый отдел имеет уникальный номер. Каждый проект имеет номер и наименование. Номер проекта является уникальным. Каждая работа из проекта имеет номер, уникальный в пределах проекта. Работы в разных проектах могут иметь одинаковые номера.
Нормальные формы отношений Пример В ходе дополнительного уточнения того, какие данные необходимо учитывать, выяснилось следующее: О каждом сотруднике необходимо хранить табельный номер и фамилию. Табельный номер является уникальным для каждого сотрудника. Каждый отдел имеет уникальный номер. Каждый проект имеет номер и наименование. Номер проекта является уникальным. Каждая работа из проекта имеет номер, уникальный в пределах проекта. Работы в разных проектах могут иметь одинаковые номера.
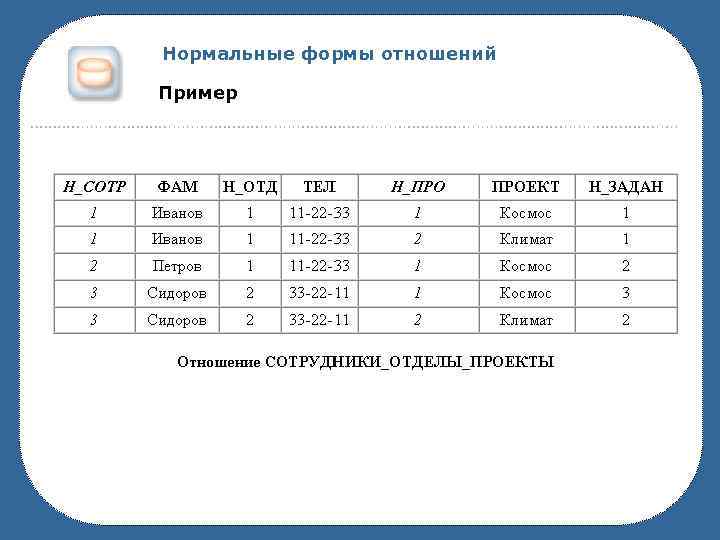
 Нормальные формы отношений Пример В ходе логического моделирования на первом шаге предложено хранить данные в одном отношении, имеющем следующие атрибуты: СОТРУДНИКИ_ОТДЕЛЫ_ПРОЕКТЫ ( Н_СОТР , ФАМ, Н_ОТД, ТЕЛ, Н_ПРО , ПРОЕКТ, Н_ЗАДАН) Н_СОТР табельный номер сотрудника ФАМ фамилия сотрудника Н_ОТД номер отдела, в котором числится сотрудник ТЕЛ телефон сотрудника Н_ПРО номер проекта, над которым работает сотрудник ПРОЕКТ наименование проекта, над которым работает сотрудник Н_ЗАДАН номер задания, над которым работает сотрудник Т. к. каждый сотрудник в каждом проекте выполняет ровно одно задание, то в качестве потенциального ключа отношения необходимо взять пару атрибутов { Н_СОТР , Н_ПРО}.
Нормальные формы отношений Пример В ходе логического моделирования на первом шаге предложено хранить данные в одном отношении, имеющем следующие атрибуты: СОТРУДНИКИ_ОТДЕЛЫ_ПРОЕКТЫ ( Н_СОТР , ФАМ, Н_ОТД, ТЕЛ, Н_ПРО , ПРОЕКТ, Н_ЗАДАН) Н_СОТР табельный номер сотрудника ФАМ фамилия сотрудника Н_ОТД номер отдела, в котором числится сотрудник ТЕЛ телефон сотрудника Н_ПРО номер проекта, над которым работает сотрудник ПРОЕКТ наименование проекта, над которым работает сотрудник Н_ЗАДАН номер задания, над которым работает сотрудник Т. к. каждый сотрудник в каждом проекте выполняет ровно одно задание, то в качестве потенциального ключа отношения необходимо взять пару атрибутов { Н_СОТР , Н_ПРО}.
 Нормальные формы отношений Пример
Нормальные формы отношений Пример
 Нормальные формы отношений Пример Данные хранятся в таблице с большой избыточностью В случае изменения состояния предметной области, при попытках соответствующим образом изменить состояние базы данных, возникает большое количество проблем: • нельзя вставить данные о сотруднике, который пока не участвует ни в одном проекте – аномалии ввода; • обновление базы данных одним действием реализовать невозможно аномалии обновления; • при удалении некоторых данных может произойти потеря другой информации аномалии удаления. Логическая модель данных неадекватна модели предметной области. База данных, основанная на такой модели, будет работать неправильно.
Нормальные формы отношений Пример Данные хранятся в таблице с большой избыточностью В случае изменения состояния предметной области, при попытках соответствующим образом изменить состояние базы данных, возникает большое количество проблем: • нельзя вставить данные о сотруднике, который пока не участвует ни в одном проекте – аномалии ввода; • обновление базы данных одним действием реализовать невозможно аномалии обновления; • при удалении некоторых данных может произойти потеря другой информации аномалии удаления. Логическая модель данных неадекватна модели предметной области. База данных, основанная на такой модели, будет работать неправильно.
 Нормальные формы отношений Нормализация основана на понятии функциональной зависимости атрибутов отношения. Каждой нормальной форме соответствует некоторый определенный набор ограничений, и отношение находится в некоторой нормальной форме, если удовлетворяет свойственному ей набору ограничений.
Нормальные формы отношений Нормализация основана на понятии функциональной зависимости атрибутов отношения. Каждой нормальной форме соответствует некоторый определенный набор ограничений, и отношение находится в некоторой нормальной форме, если удовлетворяет свойственному ей набору ограничений.
 Нормальные формы отношений Виды нормальных форм Выделяют следующие последовательности нормальных форм: • первая нормальная форма (1 NF); • вторая нормальная форма (2 NF); • третья нормальная форма (3 NF); • нормальная форма Бойса-Кодда (BCNF); • четвертая нормальная форма (4 NF); • пятая нормальная форма, или нормальная форма проекции- соединения (5 NF или PJ/NF).
Нормальные формы отношений Виды нормальных форм Выделяют следующие последовательности нормальных форм: • первая нормальная форма (1 NF); • вторая нормальная форма (2 NF); • третья нормальная форма (3 NF); • нормальная форма Бойса-Кодда (BCNF); • четвертая нормальная форма (4 NF); • пятая нормальная форма, или нормальная форма проекции- соединения (5 NF или PJ/NF).
 Нормальные формы отношений Свойства нормальных форм Основные свойства нормальных форм: • каждая следующая нормальная форма в некотором смысле лучше предыдущей; • при переходе к следующей нормальной форме свойства предыдущих нормальных свойств сохраняются. В основе процесса проектирования лежит метод нормализации, декомпозиция отношения, находящегося в предыдущей нормальной форме, в два или более отношения, удовлетворяющих требованиям следующей нормальной формы.
Нормальные формы отношений Свойства нормальных форм Основные свойства нормальных форм: • каждая следующая нормальная форма в некотором смысле лучше предыдущей; • при переходе к следующей нормальной форме свойства предыдущих нормальных свойств сохраняются. В основе процесса проектирования лежит метод нормализации, декомпозиция отношения, находящегося в предыдущей нормальной форме, в два или более отношения, удовлетворяющих требованиям следующей нормальной формы.
 Нормальные формы отношений 1 НФ (Первая Нормальная Форма) Первая нормальная форма (1 НФ) это обычное отношение, значения всех атрибутов которого атомарны. Свойства отношений (это и будут свойства 1 НФ): • В отношении нет одинаковых кортежей. • Кортежи не упорядочены. • Атрибуты не упорядочены и различаются по наименованию. • Все значения атрибутов атомарны.
Нормальные формы отношений 1 НФ (Первая Нормальная Форма) Первая нормальная форма (1 НФ) это обычное отношение, значения всех атрибутов которого атомарны. Свойства отношений (это и будут свойства 1 НФ): • В отношении нет одинаковых кортежей. • Кортежи не упорядочены. • Атрибуты не упорядочены и различаются по наименованию. • Все значения атрибутов атомарны.
 Нормальные формы отношений Функциональные зависимости Определение : В отношении R атрибут Y функционально зависит от атрибута X (X и Y могут быть составными) в том и только в том случае, если каждому значению X соответствует в точности одно значение Y: R. X (r) R. Y. Определение : Функциональная зависимость R. X (r) R. Y называется полной , если атрибут Y не зависит функционально от любого точного подмножества X.
Нормальные формы отношений Функциональные зависимости Определение : В отношении R атрибут Y функционально зависит от атрибута X (X и Y могут быть составными) в том и только в том случае, если каждому значению X соответствует в точности одно значение Y: R. X (r) R. Y. Определение : Функциональная зависимость R. X (r) R. Y называется полной , если атрибут Y не зависит функционально от любого точного подмножества X.
 Нормальные формы отношений Функциональные зависимости Определение : Неключевым атрибутом называется любой атрибут отношения, не входящий в состав первичного ключа (в частности, первичного). Определение: Функциональная зависимость R. X > R. Y называется транзитивной , если существует такой атрибут Z, что имеются функциональные зависимости R. X > R. Z и R. Z > R. Y и отсутствует функциональная зависимость R. Z > R. X. (При отсутствии последнего требования мы имели бы "неинтересные" транзитивные зависимости в любом отношении, обладающем несколькими ключами).
Нормальные формы отношений Функциональные зависимости Определение : Неключевым атрибутом называется любой атрибут отношения, не входящий в состав первичного ключа (в частности, первичного). Определение: Функциональная зависимость R. X > R. Y называется транзитивной , если существует такой атрибут Z, что имеются функциональные зависимости R. X > R. Z и R. Z > R. Y и отсутствует функциональная зависимость R. Z > R. X. (При отсутствии последнего требования мы имели бы "неинтересные" транзитивные зависимости в любом отношении, обладающем несколькими ключами).
 Нормальные формы отношений Функциональные зависимости
Нормальные формы отношений Функциональные зависимости
 Нормальные формы отношений 2 НФ (Вторая Нормальная Форма) Определение. Отношение находится во второй нормальной форме (2 НФ) тогда и только тогда, когда отношение находится в 1 НФ и нет неключевых атрибутов, зависящих от части сложного ключа. Замечание. Если потенциальный ключ отношения является простым, то отношение автоматически находится в 2 НФ.
Нормальные формы отношений 2 НФ (Вторая Нормальная Форма) Определение. Отношение находится во второй нормальной форме (2 НФ) тогда и только тогда, когда отношение находится в 1 НФ и нет неключевых атрибутов, зависящих от части сложного ключа. Замечание. Если потенциальный ключ отношения является простым, то отношение автоматически находится в 2 НФ.
 Нормальные формы отношений Пример Отношение СОТРУДНИКИ_ОТДЕЛЫ_ПРОЕКТЫ не находится в 2 НФ, т. к. есть атрибуты, зависящие от части сложного ключа:
Нормальные формы отношений Пример Отношение СОТРУДНИКИ_ОТДЕЛЫ_ПРОЕКТЫ не находится в 2 НФ, т. к. есть атрибуты, зависящие от части сложного ключа:
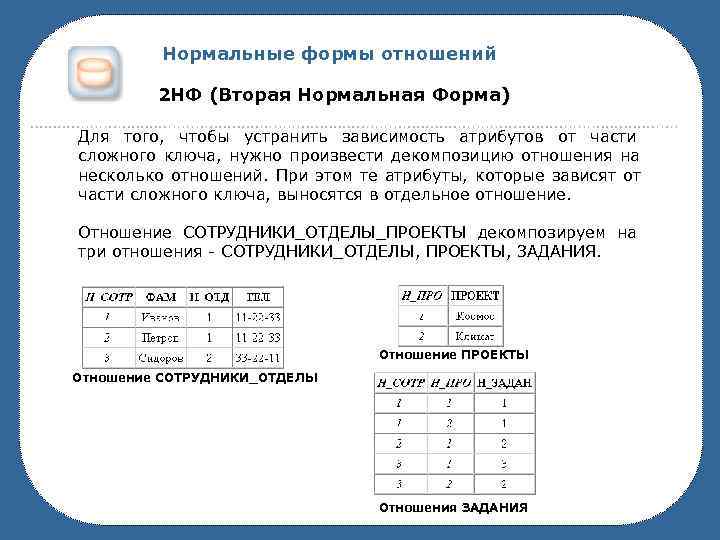
 Нормальные формы отношений 2 НФ (Вторая Нормальная Форма) Для того, чтобы устранить зависимость атрибутов от части сложного ключа, нужно произвести декомпозицию отношения на несколько отношений. При этом те атрибуты, которые зависят от части сложного ключа, выносятся в отдельное отношение. Отношение СОТРУДНИКИ_ОТДЕЛЫ_ПРОЕКТЫ декомпозируем на три отношения СОТРУДНИКИ_ОТДЕЛЫ, ПРОЕКТЫ, ЗАДАНИЯ. Отношение ПРОЕКТЫ Отношение СОТРУДНИКИ_ОТДЕЛЫ Отношения ЗАДАНИЯ
Нормальные формы отношений 2 НФ (Вторая Нормальная Форма) Для того, чтобы устранить зависимость атрибутов от части сложного ключа, нужно произвести декомпозицию отношения на несколько отношений. При этом те атрибуты, которые зависят от части сложного ключа, выносятся в отдельное отношение. Отношение СОТРУДНИКИ_ОТДЕЛЫ_ПРОЕКТЫ декомпозируем на три отношения СОТРУДНИКИ_ОТДЕЛЫ, ПРОЕКТЫ, ЗАДАНИЯ. Отношение ПРОЕКТЫ Отношение СОТРУДНИКИ_ОТДЕЛЫ Отношения ЗАДАНИЯ
 Нормальные формы отношений 3 НФ (Третья Нормальная Форма) Определение. Атрибуты называются взаимно независимыми , если ни один из них не является функционально зависимым от другого. Определение. Отношение находится в третьей нормальной форме (3 НФ) тогда и только тогда, когда отношение находится в 2 НФ и все неключевые атрибуты взаимно независимы.
Нормальные формы отношений 3 НФ (Третья Нормальная Форма) Определение. Атрибуты называются взаимно независимыми , если ни один из них не является функционально зависимым от другого. Определение. Отношение находится в третьей нормальной форме (3 НФ) тогда и только тогда, когда отношение находится в 2 НФ и все неключевые атрибуты взаимно независимы.
 Нормальные формы отношений Пример Отношение СОТРУДНИКИ_ОТДЕЛЫ не находится в 3 НФ, т. к. имеется функциональная зависимость неключевых атрибутов (зависимость номера телефона от номера отдела): Для того, чтобы устранить зависимость неключевых атрибутов, нужно произвести декомпозицию отношения на несколько отношений. При этом те неключевые атрибуты, которые являются зависимыми, выносятся в отдельное отношение. Отношение СОТРУДНИКИ_ОТДЕЛЫ декомпозируем на два отношения СОТРУДНИКИ, ОТДЕЛЫ. Отношение СОТРУДНИКИ Отношение ОТДЕЛЫ
Нормальные формы отношений Пример Отношение СОТРУДНИКИ_ОТДЕЛЫ не находится в 3 НФ, т. к. имеется функциональная зависимость неключевых атрибутов (зависимость номера телефона от номера отдела): Для того, чтобы устранить зависимость неключевых атрибутов, нужно произвести декомпозицию отношения на несколько отношений. При этом те неключевые атрибуты, которые являются зависимыми, выносятся в отдельное отношение. Отношение СОТРУДНИКИ_ОТДЕЛЫ декомпозируем на два отношения СОТРУДНИКИ, ОТДЕЛЫ. Отношение СОТРУДНИКИ Отношение ОТДЕЛЫ
 Нормальные формы отношений Алгоритм нормализации (приведение к 3 НФ) Шаг 1 (Приведение к 1 НФ). На первом шаге задается одно или несколько отношений, отображающих понятия предметной области. По модели предметной области (не по внешнему виду полученных отношений!) выписываются обнаруженные функциональные зависимости. Все отношения автоматически находятся в 1 НФ. Шаг 2 (Приведение к 2 НФ). Если в некоторых отношениях обнаружена зависимость атрибутов от части сложного ключа, то проводим декомпозицию этих отношений на несколько отношений следующим образом: те атрибуты, которые зависят от части сложного ключа выносятся в отдельное отношение вместе с этой частью ключа. В исходном отношении остаются все ключевые атрибуты. Шаг 3 (Приведение к 3 НФ). Если в некоторых отношениях обнаружена зависимость некоторых неключевых атрибутов других неключевых атрибутов, то проводим декомпозицию этих отношений следующим образом: те неключевые атрибуты, которые зависят других неключевых атрибутов выносятся в отдельное отношение. В новом отношении ключом становится детерминант функциональной зависимости
Нормальные формы отношений Алгоритм нормализации (приведение к 3 НФ) Шаг 1 (Приведение к 1 НФ). На первом шаге задается одно или несколько отношений, отображающих понятия предметной области. По модели предметной области (не по внешнему виду полученных отношений!) выписываются обнаруженные функциональные зависимости. Все отношения автоматически находятся в 1 НФ. Шаг 2 (Приведение к 2 НФ). Если в некоторых отношениях обнаружена зависимость атрибутов от части сложного ключа, то проводим декомпозицию этих отношений на несколько отношений следующим образом: те атрибуты, которые зависят от части сложного ключа выносятся в отдельное отношение вместе с этой частью ключа. В исходном отношении остаются все ключевые атрибуты. Шаг 3 (Приведение к 3 НФ). Если в некоторых отношениях обнаружена зависимость некоторых неключевых атрибутов других неключевых атрибутов, то проводим декомпозицию этих отношений следующим образом: те неключевые атрибуты, которые зависят других неключевых атрибутов выносятся в отдельное отношение. В новом отношении ключом становится детерминант функциональной зависимости
 Нормальные формы отношений Нормальная Форма Бойса - Кодда Определение. Детерминант любой атрибут, от которого полностью функционально зависит некоторый другой атрибут. Определение. Отношение находится в нормальной форме Бойса-Кодда (BCNF) в том и только в том случае, если каждый детерминант является возможным ключом.
Нормальные формы отношений Нормальная Форма Бойса - Кодда Определение. Детерминант любой атрибут, от которого полностью функционально зависит некоторый другой атрибут. Определение. Отношение находится в нормальной форме Бойса-Кодда (BCNF) в том и только в том случае, если каждый детерминант является возможным ключом.
 Нормальные формы отношений 4 НФ (Четвертая нормальная Форма) Теорема Фейджина: Отношение R (A, B, C) можно спроецировать без потерь в отношения R 1 (A, B) и R 2 (A, C) в том и только в том случае, когда существует MVD A > > B | C. Под проецированием без потерь понимается такой способ декомпозиции отношения, при котором исходное отношение полностью и без избыточности восстанавливается путем естественного соединения полученных отношений. Отношение находится в четвертой нормальной форме (4 NF) в том и только в том случае, если в случае существования многозначной зависимости A > > B все остальные атрибуты R функционально зависят от A.
Нормальные формы отношений 4 НФ (Четвертая нормальная Форма) Теорема Фейджина: Отношение R (A, B, C) можно спроецировать без потерь в отношения R 1 (A, B) и R 2 (A, C) в том и только в том случае, когда существует MVD A > > B | C. Под проецированием без потерь понимается такой способ декомпозиции отношения, при котором исходное отношение полностью и без избыточности восстанавливается путем естественного соединения полученных отношений. Отношение находится в четвертой нормальной форме (4 NF) в том и только в том случае, если в случае существования многозначной зависимости A > > B все остальные атрибуты R функционально зависят от A.
 Нормальные формы отношений 5 НФ (Пятая нормальная Форма) Определение : Отношение R (X, Y, . . . , Z) удовлетворяет зависимости соединения * (X, Y, . . . , Z) в том и только в том случае, когда R восстанавливается без потерь путем соединения своих проекций на X, Y, . . . , Z. Отношение находится в пятой нормальной форме (нормальной форме проекции соединения PJ/NF) в том и только в том случае, когда любая зависимость соединения в R следует из существования некоторого возможного ключа в R.
Нормальные формы отношений 5 НФ (Пятая нормальная Форма) Определение : Отношение R (X, Y, . . . , Z) удовлетворяет зависимости соединения * (X, Y, . . . , Z) в том и только в том случае, когда R восстанавливается без потерь путем соединения своих проекций на X, Y, . . . , Z. Отношение находится в пятой нормальной форме (нормальной форме проекции соединения PJ/NF) в том и только в том случае, когда любая зависимость соединения в R следует из существования некоторого возможного ключа в R.

