aff1e52d62008d76de960a5887810397.ppt
- Количество слайдов: 51
 Nonlinear optics at the quantum level and quantum information in optical systems Aephraim Steinberg Dept. of Physics, University of Toronto 2003 GRC on Nonlinear Optics & Lasers
Nonlinear optics at the quantum level and quantum information in optical systems Aephraim Steinberg Dept. of Physics, University of Toronto 2003 GRC on Nonlinear Optics & Lasers
 Acknowledgments U of T quantum optics & laser cooling group: PDFs: Morgan Mitchell Marcelo Martinelli Optics: Kevin Resch( Zeilinger) Jeff Lundeen Chris Ellenor Masoud Mohseni ( Lidar) Reza Mir Rob Adamson Karen Saucke (visiting from Munich) Atom Traps: Stefan Myrskog Ana Jofre Samansa Maneshi Jalani Fox Mirco Siercke Salvatore Maone ( real world) Some of our theory friends: Daniel Lidar, Janos Bergou, Mark Hillery, John Sipe, Paul Brumer, Howard Wiseman
Acknowledgments U of T quantum optics & laser cooling group: PDFs: Morgan Mitchell Marcelo Martinelli Optics: Kevin Resch( Zeilinger) Jeff Lundeen Chris Ellenor Masoud Mohseni ( Lidar) Reza Mir Rob Adamson Karen Saucke (visiting from Munich) Atom Traps: Stefan Myrskog Ana Jofre Samansa Maneshi Jalani Fox Mirco Siercke Salvatore Maone ( real world) Some of our theory friends: Daniel Lidar, Janos Bergou, Mark Hillery, John Sipe, Paul Brumer, Howard Wiseman
 OUTLINE Something you already know Introduction to quantum information with optics Something you may have known. . . but may have forgotten by now All good talks are alike. . . Making a every bad talk isinteractionown way. strong effective bad in its between two photons Something you most likely haven't heard before Quantum state and process tomography for q. info. Something you may not even buy Weak measurements -- Hardy's Paradox et cetera: "How much can we know about a photon? "
OUTLINE Something you already know Introduction to quantum information with optics Something you may have known. . . but may have forgotten by now All good talks are alike. . . Making a every bad talk isinteractionown way. strong effective bad in its between two photons Something you most likely haven't heard before Quantum state and process tomography for q. info. Something you may not even buy Weak measurements -- Hardy's Paradox et cetera: "How much can we know about a photon? "
 Intro to Quantum Info -pros & cons of optical schemes. . .
Intro to Quantum Info -pros & cons of optical schemes. . .
 Quantum Information What's so great about it?
Quantum Information What's so great about it?
 Quantum Information What's so great about it?
Quantum Information What's so great about it?
 Quantum Computer Scientists
Quantum Computer Scientists
 What makes a computer quantum?
What makes a computer quantum?
 Quantum Interference for effective single-photon–single-photon interactions. . . ?
Quantum Interference for effective single-photon–single-photon interactions. . . ?
 Can we build a two-photon switch? Photons don't interact(good for transmission; bad for computation) Nonlinear optics: photon-photon interactions generally exceedingly weak. Potential solutions: Better materials (1010 times better? !) - Want l 3 regime, but also resonant nonlinearity? - Cf. talks by Walmsley, Fejer, Gaeta, . . . Cavity QED (example of l 3 regime plus resonance) - Kimble, Haroche, Walther, Rempe, . . . EIT, slow light, etc. . . - Lukin, Fleischhauer, Harris, Scully, Hau, . . . Measurement as nonlinearity (Knill. Laflamme. Milburn) - KLM; Franson, White, . . . Other quantum interference effects? - Exchange effects in quantum NLO (Franson) ? - Interferometrically-enhanced SHG, etc (us) ?
Can we build a two-photon switch? Photons don't interact(good for transmission; bad for computation) Nonlinear optics: photon-photon interactions generally exceedingly weak. Potential solutions: Better materials (1010 times better? !) - Want l 3 regime, but also resonant nonlinearity? - Cf. talks by Walmsley, Fejer, Gaeta, . . . Cavity QED (example of l 3 regime plus resonance) - Kimble, Haroche, Walther, Rempe, . . . EIT, slow light, etc. . . - Lukin, Fleischhauer, Harris, Scully, Hau, . . . Measurement as nonlinearity (Knill. Laflamme. Milburn) - KLM; Franson, White, . . . Other quantum interference effects? - Exchange effects in quantum NLO (Franson) ? - Interferometrically-enhanced SHG, etc (us) ?
 The germ of the KLM idea INPUT STATE a|0> + b|1> + c|2> ANCILLA |1> OUTPUT STATE a'|0> + b'|1> + c'|2> TRIGGER (postselection) |1> In particular: with a similar but somewhat more complicated setup, one can engineer a |0> + b |1> + c |2> a |0> + b |1> – c |2> ; effectively a huge self-phase modulation (p per photon). More surprisingly, one can efficiently use this for scalable QC. KLM Nature 409, 46, (2001); Cf. experiments by Franson et al. , White et al. , . . .
The germ of the KLM idea INPUT STATE a|0> + b|1> + c|2> ANCILLA |1> OUTPUT STATE a'|0> + b'|1> + c'|2> TRIGGER (postselection) |1> In particular: with a similar but somewhat more complicated setup, one can engineer a |0> + b |1> + c |2> a |0> + b |1> – c |2> ; effectively a huge self-phase modulation (p per photon). More surprisingly, one can efficiently use this for scalable QC. KLM Nature 409, 46, (2001); Cf. experiments by Franson et al. , White et al. , . . .
 The mad, mad idea of Jim Franson J. D. Franson, Phys. Rev. Lett 78, 3852 (1997) Nonlinear coefficients scale linearly with the number of atoms. Could the different atoms' effects be made to add coherently, providing an N 2 enhancement (where N might be 1013)? atom 1 w 2 atom 2 w 1 Appears to violate local energy conservation. . . but consists of perfectly reasonable Feynman diagrams, with energy conserved in final state. {Controversy regarding some magic cancellations. . } Each of N(N-1)/2 pairs of atoms should contribute. Franson proposes that this can lead to immense nonlinearities. No conclusive data.
The mad, mad idea of Jim Franson J. D. Franson, Phys. Rev. Lett 78, 3852 (1997) Nonlinear coefficients scale linearly with the number of atoms. Could the different atoms' effects be made to add coherently, providing an N 2 enhancement (where N might be 1013)? atom 1 w 2 atom 2 w 1 Appears to violate local energy conservation. . . but consists of perfectly reasonable Feynman diagrams, with energy conserved in final state. {Controversy regarding some magic cancellations. . } Each of N(N-1)/2 pairs of atoms should contribute. Franson proposes that this can lead to immense nonlinearities. No conclusive data.
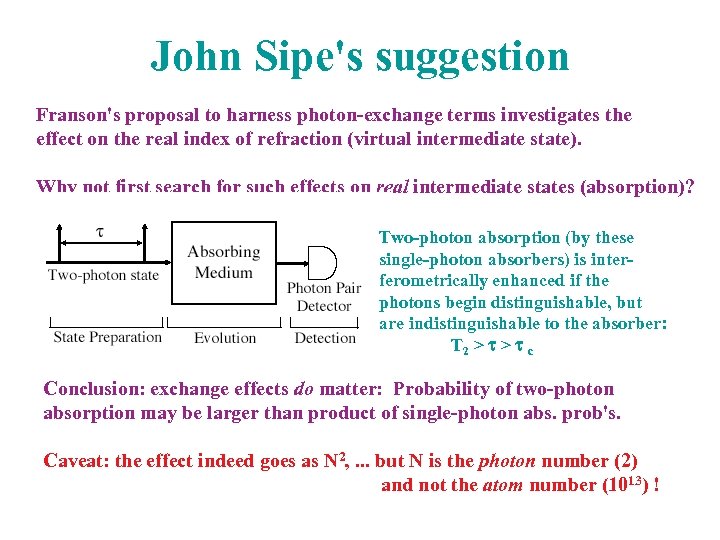 John Sipe's suggestion Franson's proposal to harness photon-exchange terms investigates the effect on the real index of refraction (virtual intermediate state). Why not first search for such effects on real intermediate states (absorption)? Two-photon absorption (by these single-photon absorbers) is interferometrically enhanced if the photons begin distinguishable, but are indistinguishable to the absorber: T 2 > t c Conclusion: exchange effects do matter: Probability of two-photon absorption may be larger than product of single-photon abs. prob's. Caveat: the effect indeed goes as N 2, . . . but N is the photon number (2) and not the atom number (1013) !
John Sipe's suggestion Franson's proposal to harness photon-exchange terms investigates the effect on the real index of refraction (virtual intermediate state). Why not first search for such effects on real intermediate states (absorption)? Two-photon absorption (by these single-photon absorbers) is interferometrically enhanced if the photons begin distinguishable, but are indistinguishable to the absorber: T 2 > t c Conclusion: exchange effects do matter: Probability of two-photon absorption may be larger than product of single-photon abs. prob's. Caveat: the effect indeed goes as N 2, . . . but N is the photon number (2) and not the atom number (1013) !
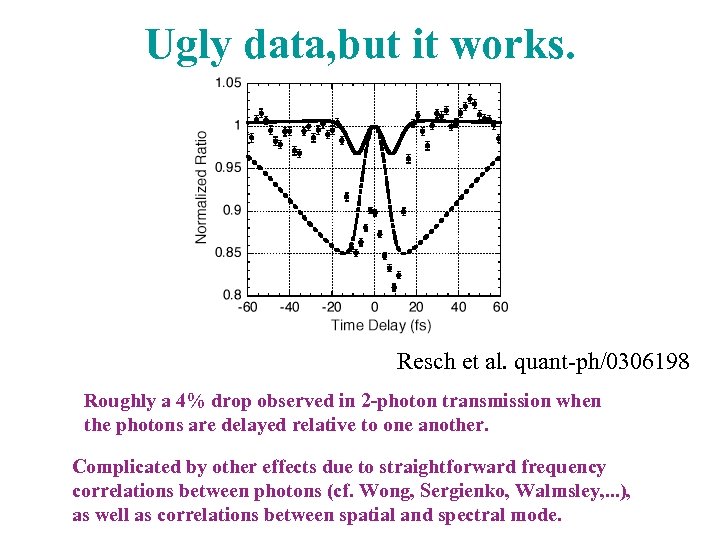 Ugly data, but it works. Resch et al. quant-ph/0306198 Roughly a 4% drop observed in 2 -photon transmission when the photons are delayed relative to one another. Complicated by other effects due to straightforward frequency correlations between photons (cf. Wong, Sergienko, Walmsley, . . . ), as well as correlations between spatial and spectral mode.
Ugly data, but it works. Resch et al. quant-ph/0306198 Roughly a 4% drop observed in 2 -photon transmission when the photons are delayed relative to one another. Complicated by other effects due to straightforward frequency correlations between photons (cf. Wong, Sergienko, Walmsley, . . . ), as well as correlations between spatial and spectral mode.
 What was the setup? Type-II SPDC + birefringent delay + 45 o polarizer produces delayed pairs. Use a reflective notch filter as absorbing medium, and detect remaining pairs. This is just a Hong-Ou-Mandel interferometer, with detection in a complementary mode. Although the filter is placed after the output, this is irrelevant for a linear system. Interpretations: • Our "suppressed" two-photon reflection is merely the ratio of two different interference patterns; the modified spectrum broadens the pattern. • Yet photons which reach the filter in pairs really do not behave independently. HOM interference pattern is itself a manifestation of photon exchange effects. The
What was the setup? Type-II SPDC + birefringent delay + 45 o polarizer produces delayed pairs. Use a reflective notch filter as absorbing medium, and detect remaining pairs. This is just a Hong-Ou-Mandel interferometer, with detection in a complementary mode. Although the filter is placed after the output, this is irrelevant for a linear system. Interpretations: • Our "suppressed" two-photon reflection is merely the ratio of two different interference patterns; the modified spectrum broadens the pattern. • Yet photons which reach the filter in pairs really do not behave independently. HOM interference pattern is itself a manifestation of photon exchange effects. The
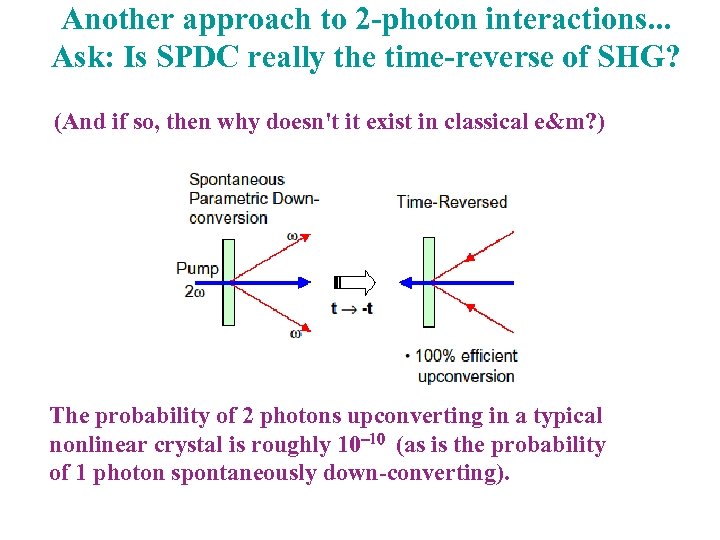 Another approach to 2 -photon interactions. . . Ask: Is SPDC really the time-reverse of SHG? (And if so, then why doesn't it exist in classical e&m? ) The probability of 2 photons upconverting in a typical nonlinear crystal is roughly 10 -10 (as is the probability of 1 photon spontaneously down-converting).
Another approach to 2 -photon interactions. . . Ask: Is SPDC really the time-reverse of SHG? (And if so, then why doesn't it exist in classical e&m? ) The probability of 2 photons upconverting in a typical nonlinear crystal is roughly 10 -10 (as is the probability of 1 photon spontaneously down-converting).
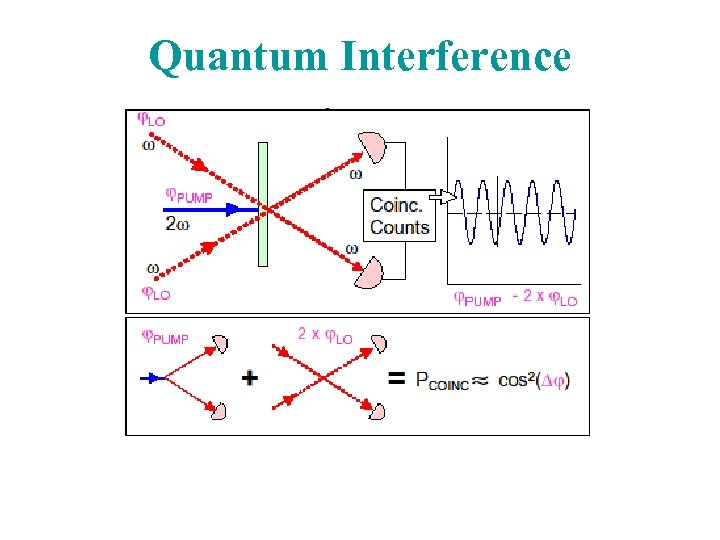 Quantum Interference
Quantum Interference
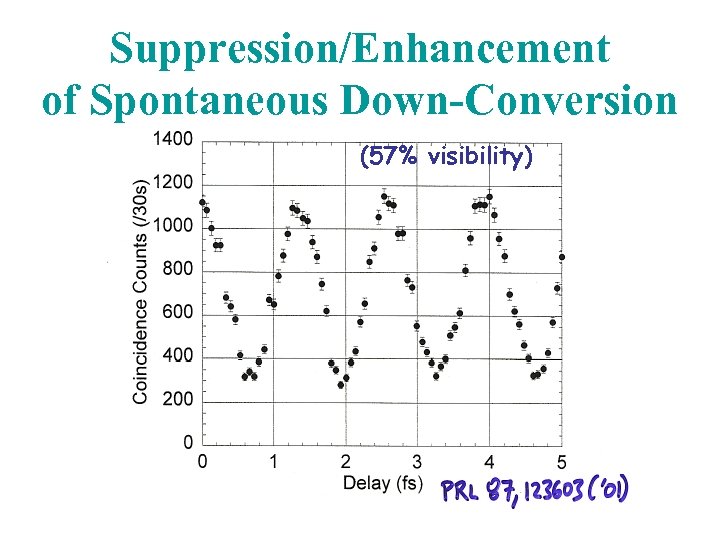 Suppression/Enhancement of Spontaneous Down-Conversion (57% visibility)
Suppression/Enhancement of Spontaneous Down-Conversion (57% visibility)
 Photon-photon transmission switch On average, less than one photon per pulse. One photon present in a given pulse is sufficient to switch off transmission. The photons upconvert with near-unit eff. (Peak power approx. m. W/cm 2). The blue pump serves as a catalyst, enhancing the interaction by 1010.
Photon-photon transmission switch On average, less than one photon per pulse. One photon present in a given pulse is sufficient to switch off transmission. The photons upconvert with near-unit eff. (Peak power approx. m. W/cm 2). The blue pump serves as a catalyst, enhancing the interaction by 1010.
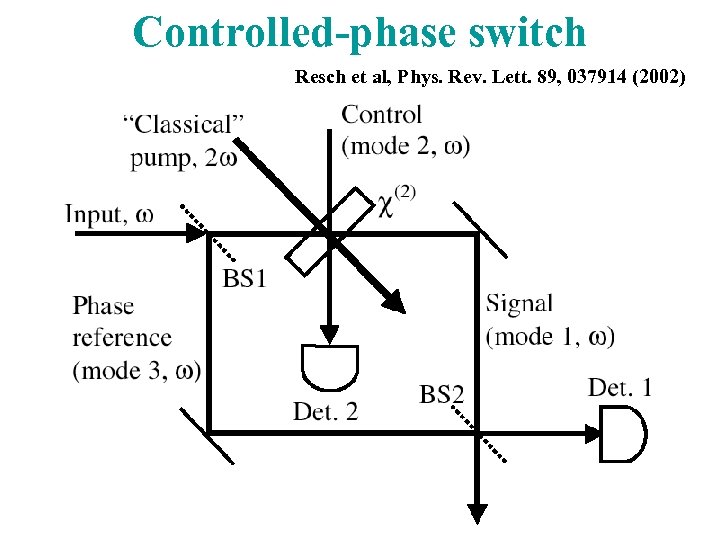 Controlled-phase switch Resch et al, Phys. Rev. Lett. 89, 037914 (2002)
Controlled-phase switch Resch et al, Phys. Rev. Lett. 89, 037914 (2002)
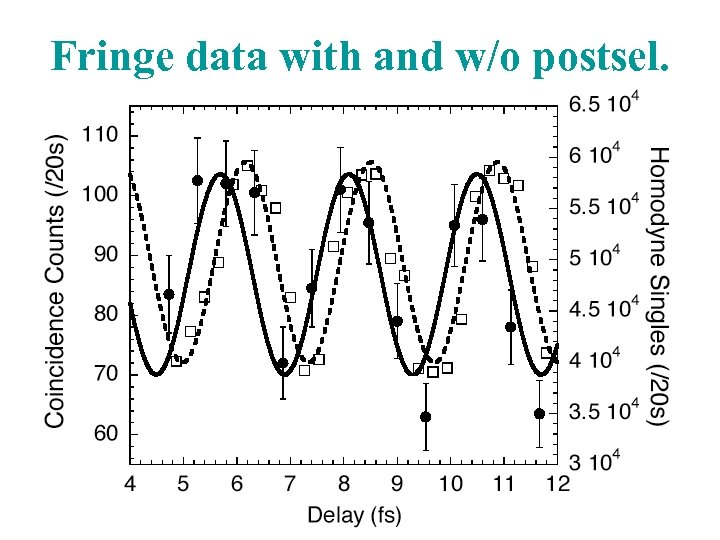 Fringe data with and w/o postsel.
Fringe data with and w/o postsel.
 So why don't we "rule the world"? N. B. : This switch relies on interference. Input state must have specific phase. Single photons don't have well-defined phase. The switch does not work on Fock states. The phase shifts if and only if a control photon is present-so long as we make sure not to know in advance whether or not it is present. Another example of postselected logic. Nonetheless: Have shown theoretically that a polarisation version could be used for Bell-state determination (and, e. g. , dense coding)… a task known to be impossible with LO. [Resch et al. , quant-ph/0204034] Present "application, " however, is to a novel test of QM (later in this talk, with any luck. . . ).
So why don't we "rule the world"? N. B. : This switch relies on interference. Input state must have specific phase. Single photons don't have well-defined phase. The switch does not work on Fock states. The phase shifts if and only if a control photon is present-so long as we make sure not to know in advance whether or not it is present. Another example of postselected logic. Nonetheless: Have shown theoretically that a polarisation version could be used for Bell-state determination (and, e. g. , dense coding)… a task known to be impossible with LO. [Resch et al. , quant-ph/0204034] Present "application, " however, is to a novel test of QM (later in this talk, with any luck. . . ).
 Characterisation of quantum processes in QI systems
Characterisation of quantum processes in QI systems
 Quantum State/Process Tomography • "Pre"-QI: Wigner function for nonclassical light (Raymer et al), molecules (Walmsley et al), et cetera • Kwiat/White et al. : tomography of entangled photons; entanglement-assisted tomography • Jessen et al. : density matrix reconstruction for high-spin state (9 x 9 density matrix in F=4 Cs) • Cory et al. : use of superoperator to design QEC pulse sequences for NMR (QFT etc) • Many, many people I've omitted. . .
Quantum State/Process Tomography • "Pre"-QI: Wigner function for nonclassical light (Raymer et al), molecules (Walmsley et al), et cetera • Kwiat/White et al. : tomography of entangled photons; entanglement-assisted tomography • Jessen et al. : density matrix reconstruction for high-spin state (9 x 9 density matrix in F=4 Cs) • Cory et al. : use of superoperator to design QEC pulse sequences for NMR (QFT etc) • Many, many people I've omitted. . .
 Density matrices and superoperators
Density matrices and superoperators
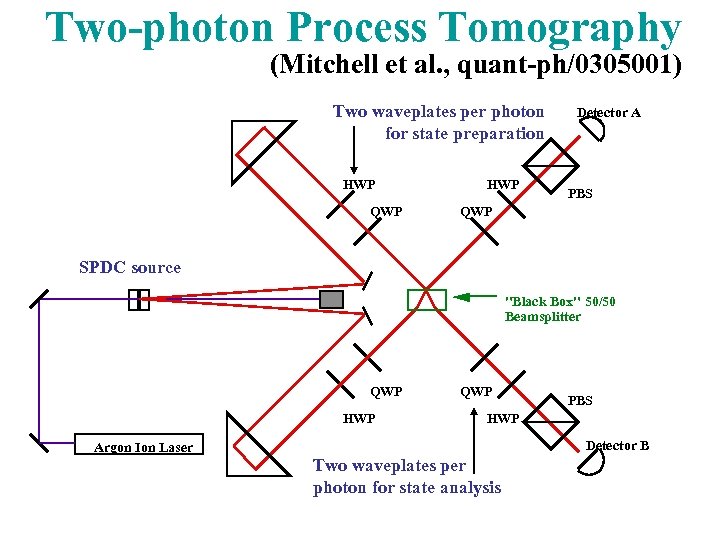 Two-photon Process Tomography (Mitchell et al. , quant-ph/0305001) Two waveplates per photon for state preparation HWP QWP HWP Detector A PBS QWP SPDC source "Black Box" 50/50 Beamsplitter QWP HWP Argon Ion Laser QWP PBS HWP Detector B Two waveplates per photon for state analysis
Two-photon Process Tomography (Mitchell et al. , quant-ph/0305001) Two waveplates per photon for state preparation HWP QWP HWP Detector A PBS QWP SPDC source "Black Box" 50/50 Beamsplitter QWP HWP Argon Ion Laser QWP PBS HWP Detector B Two waveplates per photon for state analysis
 Hong-Ou-Mandel Interference r r + t t How often will both detectors fire together? r 2+t 2 = 0; total destructive interf. (if photons indistinguishable). If the photons begin in a symmetric state, no coincidences. {Exchange effect; cf. behaviour of fermions in analogous setup!} The only antisymmetric state is the singlet state |HV> – |VH>, in which each photon is unpolarized but the two are orthogonal. This interferometer is a "Bell-state filter, " needed for quantum teleportation and other applications. Our Goal: use process tomography to test this filter.
Hong-Ou-Mandel Interference r r + t t How often will both detectors fire together? r 2+t 2 = 0; total destructive interf. (if photons indistinguishable). If the photons begin in a symmetric state, no coincidences. {Exchange effect; cf. behaviour of fermions in analogous setup!} The only antisymmetric state is the singlet state |HV> – |VH>, in which each photon is unpolarized but the two are orthogonal. This interferometer is a "Bell-state filter, " needed for quantum teleportation and other applications. Our Goal: use process tomography to test this filter.
 Comparison to ideal filter Measured superoperator, in Bell-state basis: Superoperator after transformation to correct polarisation rotations: A singlet-state filter would have a single peak, indicating the one transmitted state. Dominated by a single peak; residuals allow us to estimate degree of decoherence and other errors.
Comparison to ideal filter Measured superoperator, in Bell-state basis: Superoperator after transformation to correct polarisation rotations: A singlet-state filter would have a single peak, indicating the one transmitted state. Dominated by a single peak; residuals allow us to estimate degree of decoherence and other errors.
 Tomography in Optical Lattices Atoms trapped in standing waves of light are a promising medium for QIP. (Deutsch/Jessen, Cirac/Zoller, Bloch, . . . ) We would like to characterize their time-evolution & decoherence. First: must learn how to measure state populations in a lattice…
Tomography in Optical Lattices Atoms trapped in standing waves of light are a promising medium for QIP. (Deutsch/Jessen, Cirac/Zoller, Bloch, . . . ) We would like to characterize their time-evolution & decoherence. First: must learn how to measure state populations in a lattice…
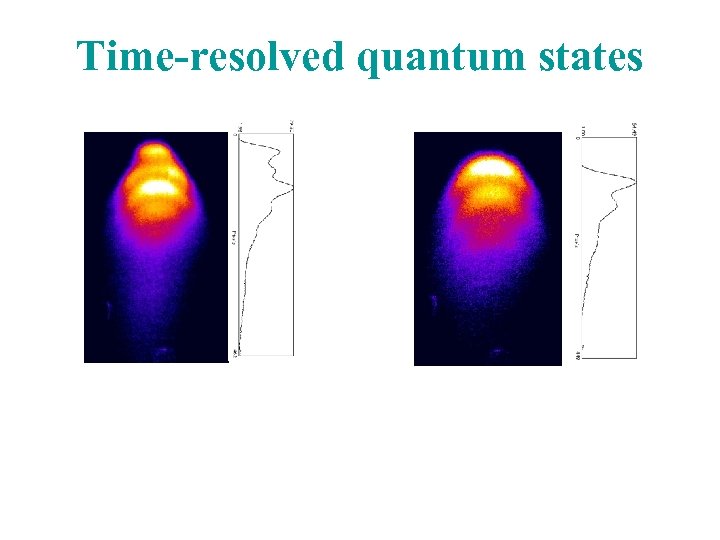 Time-resolved quantum states
Time-resolved quantum states
 Quantum state reconstruction Dx Wait… Measure ground state population (OR: can now translate in x and p directly. . . ) Shift…
Quantum state reconstruction Dx Wait… Measure ground state population (OR: can now translate in x and p directly. . . ) Shift…
 Create a coherent state by shifting lattice; delay and shift to measure W.
Create a coherent state by shifting lattice; delay and shift to measure W.
 A different value of the delay
A different value of the delay
 Oscillations in lattice wells Ground-state population vs. time bet. translations Fancy NLO interpretation: Raman pump-probe study of vibrational states
Oscillations in lattice wells Ground-state population vs. time bet. translations Fancy NLO interpretation: Raman pump-probe study of vibrational states
 Exp't: "W" or [Pg-Pe](x, p)
Exp't: "W" or [Pg-Pe](x, p)
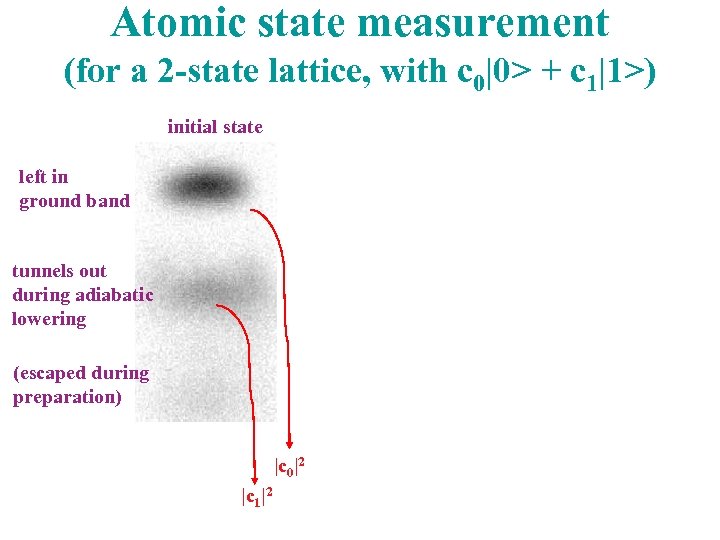 Atomic state measurement (for a 2 -state lattice, with c 0|0> + c 1|1>) initial state displaced delayed & displaced left in ground band tunnels out during adiabatic lowering (escaped during preparation) |c 0|2 |c 1|2 |c 0 + c 1 |2 |c 0 + i c 1 |2
Atomic state measurement (for a 2 -state lattice, with c 0|0> + c 1|1>) initial state displaced delayed & displaced left in ground band tunnels out during adiabatic lowering (escaped during preparation) |c 0|2 |c 1|2 |c 0 + c 1 |2 |c 0 + i c 1 |2
 Time-evolution of some states input density matrices output density matrices
Time-evolution of some states input density matrices output density matrices
 Atom superoperators sitting in lattice, quietly decohering… being shaken back and forth resonantly Initial Bloch sphere CURRENT PROJECTS: On atoms, incorporate "bang-bang" (pulse echo) to preserve coherence & measure homog. linewidth. With photons, study "tailored" quantum error correction (adaptive encodings for collective noise).
Atom superoperators sitting in lattice, quietly decohering… being shaken back and forth resonantly Initial Bloch sphere CURRENT PROJECTS: On atoms, incorporate "bang-bang" (pulse echo) to preserve coherence & measure homog. linewidth. With photons, study "tailored" quantum error correction (adaptive encodings for collective noise).
 Can we talk about what goes on behind closed doors?
Can we talk about what goes on behind closed doors?
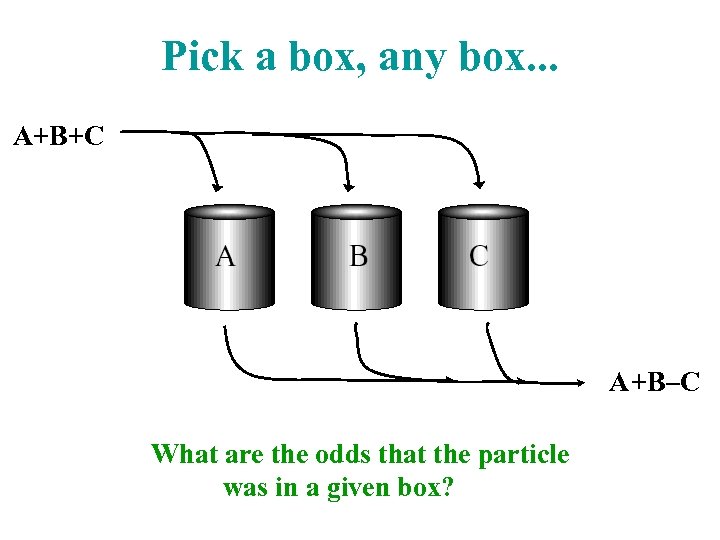 Pick a box, any box. . . A+B+C A +B–C What are the odds that the particle was in a given box?
Pick a box, any box. . . A+B+C A +B–C What are the odds that the particle was in a given box?
 Conditional measurements (Aharonov, Albert, and Vaidman) AAV, PRL 60, 1351 ('88) Prepare a particle in |i> …try to "measure" some observable A… postselect the particle to be in |f> Measurement of A Does depend more on i or f, or equally on both? Clever answer: both, as Schrödinger time-reversible. Conventional answer: i, because of collapse.
Conditional measurements (Aharonov, Albert, and Vaidman) AAV, PRL 60, 1351 ('88) Prepare a particle in |i> …try to "measure" some observable A… postselect the particle to be in |f> Measurement of A Does depend more on i or f, or equally on both? Clever answer: both, as Schrödinger time-reversible. Conventional answer: i, because of collapse.
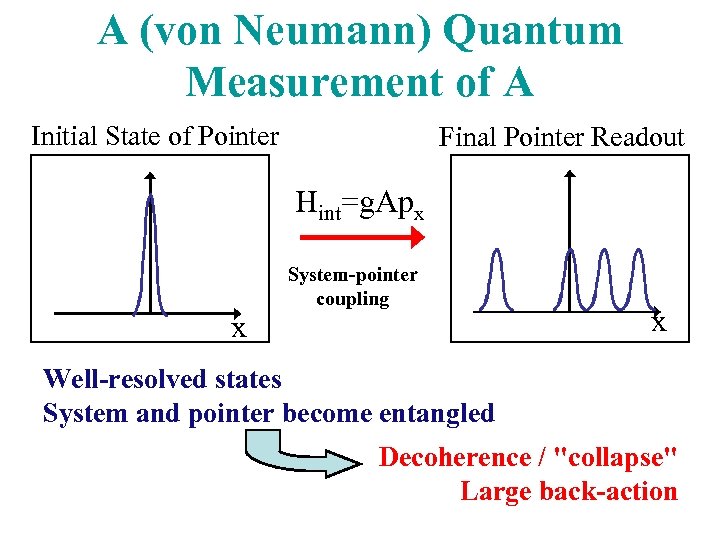 A (von Neumann) Quantum Measurement of A Initial State of Pointer Final Pointer Readout Hint=g. Apx x System-pointer coupling x Well-resolved states System and pointer become entangled Decoherence / "collapse" Large back-action
A (von Neumann) Quantum Measurement of A Initial State of Pointer Final Pointer Readout Hint=g. Apx x System-pointer coupling x Well-resolved states System and pointer become entangled Decoherence / "collapse" Large back-action
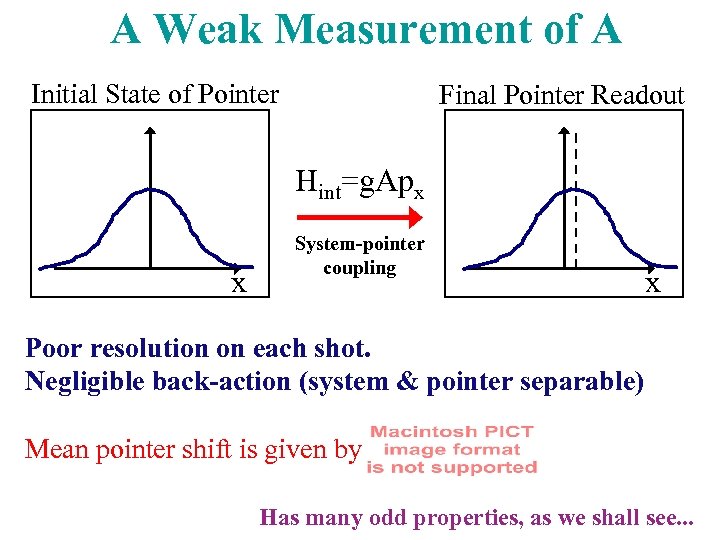 A Weak Measurement of A Initial State of Pointer Final Pointer Readout Hint=g. Apx x System-pointer coupling x Poor resolution on each shot. Negligible back-action (system & pointer separable) Mean pointer shift is given by Has many odd properties, as we shall see. . .
A Weak Measurement of A Initial State of Pointer Final Pointer Readout Hint=g. Apx x System-pointer coupling x Poor resolution on each shot. Negligible back-action (system & pointer separable) Mean pointer shift is given by Has many odd properties, as we shall see. . .
 "Interaction-Free Measurements" (AKA: The Elitzur-Vaidman bomb experiment) A. C. Elitzur, and L. Vaidman, Found. Phys. 23, 987 (1993) Problem: D C Consider a collection of bombs so sensitive that a collision with any single particle (photon, electron, etc. ) Bomb absent: is guarranteed to trigger it. Only detector C fires BS 2 Suppose that certain of the bombs are defective, but differ in their behaviour in no way other than that Bomb present: they will not blow up when triggered. "boom!" 1/2 Is there any way to identify the working bombs (or C some of them) without blowing them up? 1/4 BS 1 D 1/4
"Interaction-Free Measurements" (AKA: The Elitzur-Vaidman bomb experiment) A. C. Elitzur, and L. Vaidman, Found. Phys. 23, 987 (1993) Problem: D C Consider a collection of bombs so sensitive that a collision with any single particle (photon, electron, etc. ) Bomb absent: is guarranteed to trigger it. Only detector C fires BS 2 Suppose that certain of the bombs are defective, but differ in their behaviour in no way other than that Bomb present: they will not blow up when triggered. "boom!" 1/2 Is there any way to identify the working bombs (or C some of them) without blowing them up? 1/4 BS 1 D 1/4
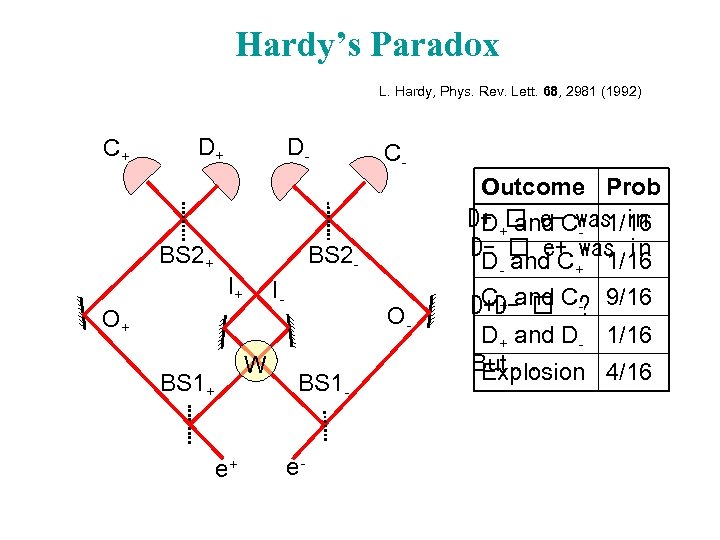 Hardy’s Paradox L. Hardy, Phys. Rev. Lett. 68, 2981 (1992) C+ D+ D- BS 2+ C- BS 2 I+ I- O+ W BS 1+ e+ OBS 1 e- Outcome Prob D+ + e-Cwas in D and - 1/16 D- e+ was in D- and C+ 1/16 C+ D+D-and C-? 9/16 D+ and D- 1/16 But … Explosion 4/16
Hardy’s Paradox L. Hardy, Phys. Rev. Lett. 68, 2981 (1992) C+ D+ D- BS 2+ C- BS 2 I+ I- O+ W BS 1+ e+ OBS 1 e- Outcome Prob D+ + e-Cwas in D and - 1/16 D- e+ was in D- and C+ 1/16 C+ D+D-and C-? 9/16 D+ and D- 1/16 But … Explosion 4/16
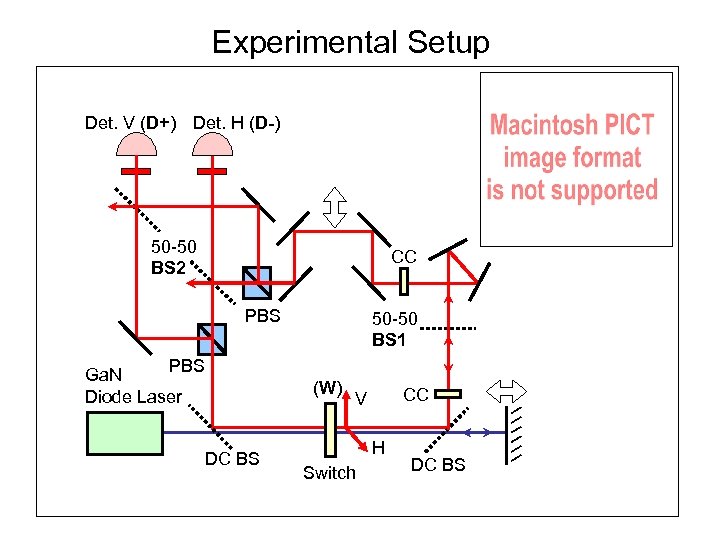 Experimental Setup Det. V (D+) Det. H (D-) 50 -50 BS 2 CC PBS Ga. N Diode Laser 50 -50 BS 1 (W) DC BS CC V H Switch DC BS
Experimental Setup Det. V (D+) Det. H (D-) 50 -50 BS 2 CC PBS Ga. N Diode Laser 50 -50 BS 1 (W) DC BS CC V H Switch DC BS


 But what can we say about where the particles were or weren't, once D+ & D– fire? Probabilities e- in e+ in 0 e- out 1 1 e+ out 1 -1 0 Upcoming experiment: demonstrate that "weak measurements" (à la Aharonov + Vaidman) will bear out these predictions.
But what can we say about where the particles were or weren't, once D+ & D– fire? Probabilities e- in e+ in 0 e- out 1 1 e+ out 1 -1 0 Upcoming experiment: demonstrate that "weak measurements" (à la Aharonov + Vaidman) will bear out these predictions.
 PROBLEM SOLVED!(? )
PROBLEM SOLVED!(? )
 SUMMARY • Quantum interference allows huge enhancements of effective optical nonlinearities. How do they relate to"real" nonlinearities? What are or aren't they good for? • Two-photon switch useful for studies of quantum weirdness (Hardy's paradox, weak measurement), and Bell-state detection. • Two-photon process tomography useful for characterizing various candidate QI systems. Next round of experiments on tailored quantum error correction (w/ D. Lidar et al. ). • As we learn to control individual quantum systems, more and more applications of postselection appear; need to learn how to think about postselected subensembles (weak measurement, conditional logic, et cetera). (see Steinberg, quant-ph/0302003) • No matter what the Silicon crowd thinks, there's a lot of mileage left in (nonlinear/quantum) optics!
SUMMARY • Quantum interference allows huge enhancements of effective optical nonlinearities. How do they relate to"real" nonlinearities? What are or aren't they good for? • Two-photon switch useful for studies of quantum weirdness (Hardy's paradox, weak measurement), and Bell-state detection. • Two-photon process tomography useful for characterizing various candidate QI systems. Next round of experiments on tailored quantum error correction (w/ D. Lidar et al. ). • As we learn to control individual quantum systems, more and more applications of postselection appear; need to learn how to think about postselected subensembles (weak measurement, conditional logic, et cetera). (see Steinberg, quant-ph/0302003) • No matter what the Silicon crowd thinks, there's a lot of mileage left in (nonlinear/quantum) optics!


