0af3ed49ec2b7c1ffbcbe95c1fe63578.ppt
- Количество слайдов: 35

Nonlinear Model-Based Estimation Algorithms: Tutorial and Recent Developments Mark L. Psiaki Sibley School of Mechanical & Aerospace Engr. , Cornell University Aero. Engr. & Engr. Mech. , UT Austin 31 March 2011

Acknowledgements n n Collaborators q Paul Kintner, former Cornell ECE faculty member q Steve Powell, Cornell ECE research engineer q Hee Jung, Eric Klatt, Todd Humphreys, & Shan Mohiuddin, Cornell GPS group Ph. D. alumni q Joanna Hinks, Ryan Dougherty, Ryan Mitch, & Karen Chiang, Cornell GPS group Ph. D. candidates q Jon Schoenberg & Isaac Miller, Cornell Ph. D. candidate/alumnus of Prof. M. Campbell’s autonomous systems group q Prof. Yaakov Oshman, The Technion, Haifa, Israel, faculty of Aerospace Engineering q Massaki Wada, Saila System Inc. of Tokyo, Japan Sponsors q Boeing Integrated Defense Systems q NASA Goddard q NASA OSS q NSF UT Austin March ‘ 11 2 of 35

Goals: n n Use sensor data from nonlinear systems to infer internal states or hidden parameters Enable navigation, autonomous control, etc. in challenging environments (e. g. , heavy GPS jamming) or with limited/simplified sensor suites Strategies: n n Develop models of system dynamics & sensors that relate internal states or hidden parameters to sensor outputs Use nonlinear estimation to “invert” models & determine states or parameters that are not directly measured q q q Nonlinear least-squares Kalman filtering Bayesian probability analysis UT Austin March ‘ 11 3 of 35

Outline I. III. IV. V. VI. VIII. Related research Example problem: Blind tricyclist w/bearings-only measurements to uncertain target locations Observability/minimum sensor suite Batch filter estimation § Math model of tricyclist problem § Linearized observability analysis § Nonlinear least-squares solution Models w/process noise, batch filter limitations Nonlinear dynamic estimators: mechanizations & performance § Extended Kalman Filter (EKF) § Sigma-points filter/Unscented Kalman Filter (UKF) § Particle filter (PF) § Backwards-smoothing EKF (BSEKF) Introduction of Gaussian sum techniques Summary & conclusions UT Austin March ‘ 11 4 of 35

Related Research n n n Nonlinear least squares batch estimation: Extensive literature & textbooks, – e. g. , Gill, Murray, & Wright (1981) Kalman filter & EKF: Extensive literature & textbooks, e. g. , Brown & Hwang 1997 or Bar-Shalom, Li & Kirubarajan (2001) Sigma-points filter/UKF: Julier, Uhlmann, & Durrant-Whyte (2000), Wan & van der Merwe (2001), … etc. Particle filter: Gordon, Salmond, & Smith (1993), Arulampalam et al. tutorial (2002), … etc. Backwards-smoothing EKF: Psiaki (2005) Gaussian mixture filter: Sorenson & Alspach (1971), van der Merwe & Wan (2003), Psiaki, Schoenberg, & Miller (2010), … etc. UT Austin March ‘ 11 5 of 35

A Blind Tricyclist Measuring Relative Bearing to a Friend on a Merry-Go-Round n Assumptions/constraints: q q q n Tricyclist doesn’t know initial x-y position or heading, but can accurately accumulate changes in location & heading via dead-reckoning Friend of tricyclist rides a merry-go-round & periodically calls to him giving him a relative bearing measurement Tricyclist knows merry-go-round location & diameter, but not its initial orientation or its constant rotation rate Estimation problem: determine initial location & heading plus merry-go-round initial orientation & rotation rate UT Austin March ‘ 11 6 of 35

Example Tricycle Trajectory & Relative Bearing Measurements n See 1 st Matlab movie UT Austin March ‘ 11 7 of 35

Is the System Observable? n n Observability is condition of having unique internal states/parameters that produce a given measurement time history Verify observability before designing an estimator because estimation algorithms do not work for unobservable systems q q n Linear system observability tested via matrix rank calculations Nonlinear system observability tested via local linearization rank calculations & global minimum considerations of associated leastsquares problem Failed observability test implies need for additional sensing UT Austin March ‘ 11 8 of 35

Observability Failure of Tricycle Problem & a Fix n n See 2 nd Matlab movie for failure/nonuniqueness See 3 rd Matlab movie for fix via additional sensing UT Austin March ‘ 11 9 of 35
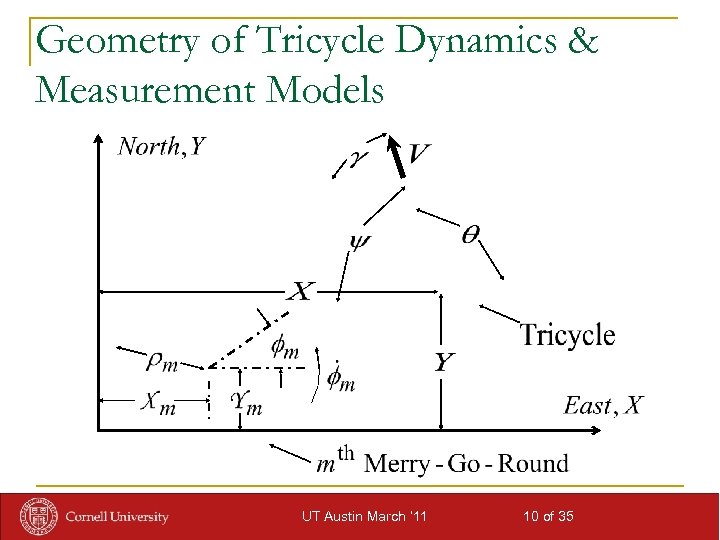
Geometry of Tricycle Dynamics & Measurement Models UT Austin March ‘ 11 10 of 35

Tricycle Dynamics Model from Kinematics n Constant-turn-radius transition from tk to tk+1 = tk +Dt: n State & control vector definitions n Consistent with standard discrete-time state-vector dynamic model form: UT Austin March ‘ 11 11 of 35

Bearing Measurement Model n Trigonometry of bearing measurement to mth merry-go -round rider n Sample-dependent measurement vector definition: n Consistent with standard discrete-time state-vector measurement model form: UT Austin March ‘ 11 12 of 35

Nonlinear Batch Filter Model n Over-determined system of equations: n Definitions of vectors & model function: UT Austin March ‘ 11 13 of 35

Batch Filter Observability & Estimation n Linearized local observability analysis: n Batch filter nonlinear least-squares estimation problem n Approximate estimation error covariance UT Austin March ‘ 11 14 of 35
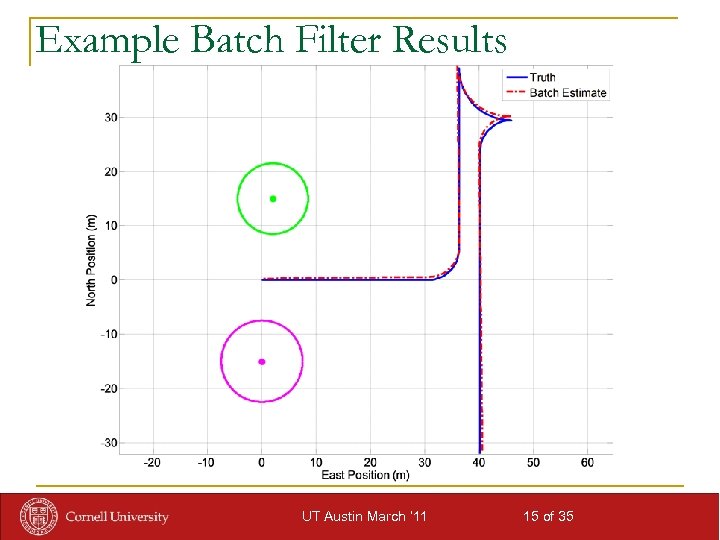
Example Batch Filter Results UT Austin March ‘ 11 15 of 35

Dynamic Models with Process Noise n Typical form driven by Gaussian white random process noise vk: n Tricycle problem dead-reckoning errors naturally modeled as process noise Specific process noise terms n q q Random errors between true speed V & true steer angle g and the measured values used for dead-reckoning Wheel slip that causes odometry errors or that occurs in the side-slip direction. UT Austin March ‘ 11 16 of 35

Effect of Process Noise on Truth Trajectory UT Austin March ‘ 11 17 of 35

Effect of Process Noise on Batch Filter UT Austin March ‘ 11 18 of 35

Dynamic Filtering based on Bayesian Conditional Probability Density subject to xi for i = 0, …, k-1 determined as functions of xk & v 0, …, vk-1 via inversion of the equations: UT Austin March ‘ 11 19 of 35

EKF Approximation n Uses Taylor series approximations of fk(xk, uk, vk) & hk(xk) q q n Gaussian statistics assumed q q q n Taylor expansions about approximate xk expectation values & about vk = 0 Normally only first-order, i. e. , linear, expansions used, but sometimes quadratic terms are used Allows complete probability density characterization in terms of means & covariances Allows closed-form mean & covariance propagations Optimal for truly linear, truly Gaussian systems Drawbacks q q Requires encoding of analytic derivatives Loses accuracy or even stability in the presence of severe nonlinearities UT Austin March ‘ 11 20 of 35

EKF Performance, Moderate Initial Uncertainty UT Austin March ‘ 11 21 of 35

EKF Performance, Large Initial Uncertainty UT Austin March ‘ 11 22 of 35

Sigma-Points UKF Approximation n Evaluate fk(xk, uk, vk) & hk(xk) at specially chosen “sigma” points & compute statistics of results q q n Gaussian statistics assumed, as in EKF q q n “Sigma” points & weights yield pseudo-random approximate Monte-Carlo calculations Can be tuned to match statistical effects of more Taylor series terms than EKF approximation Mean & covariance assumed to fully characterize distribution Sigma points provide a describing-function-type method for improving mean & covariance propagations, which are performed via weighted averaging over sigma points No need for analytic derivatives of functions Also optimal for truly linear, truly Gaussian systems Drawback q q q Additional Taylor series approximation accuracy may not be sufficient for severe nonlinearities Extra parameters to tune Singularities & discontinuities may hurt UKF more than other filters UT Austin March ‘ 11 23 of 35

UKF Performance, Moderate Initial Uncertainty UT Austin March ‘ 11 24 of 35

UKF Performance, Large Initial Uncertainty UT Austin March ‘ 11 25 of 35

Particle Filter Approximation n Approximate the conditional probability distribution using Monte-Carlo techniques q q q n Advantages q q q n Keep track of a large number of state samples & corresponding weights Update weights based on relative goodness of their fits to measured data Re-sample distribution if weights become overly skewed to a few points, using regularization to avoid point degeneracy No need for Gaussian assumption Evaluates fk(xk, uk, vk) & hk(xk) at many points, does not need analytic derivatives Theoretically exact in the limit of large numbers of points Drawbacks q q Point degeneracy due to skewed weights not fully compensated by regularization Too many points required for accuracy/convergence robustness for highdimensional problems UT Austin March ‘ 11 26 of 35

PF Performance, Moderate Initial Uncertainty UT Austin March ‘ 11 27 of 35

PF Performance, Large Initial Uncertainty UT Austin March ‘ 11 28 of 35

Backwards-Smoothing EKF Approximation n Maximizes probability density instead of trying to approximate intractable integrals q q q n Maximum a posteriori (MAP) estimation can be biased, but also can be very near optimal Standard numerical trajectory optimization-type techniques can be used to form estimates Performs explicit re-estimation of a number of past process noise vectors & explicitly considers a number of past measurements in addition to the current one, re-linearizing many fi(xi, ui, vi) & hi(xi) for values of i <= k as part of a non-linear smoothing calculation Drawbacks q q q Computationally intensive, though highly parallelizable MAP not good for multi-modal distributions Tuning parameters adjust span & solution accuracy of re-smoothing problems UT Austin March ‘ 11 29 of 35
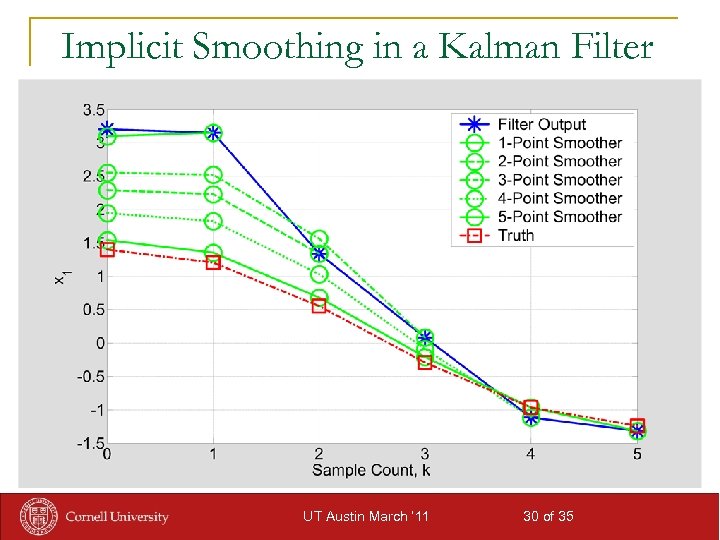
Implicit Smoothing in a Kalman Filter UT Austin March ‘ 11 30 of 35

BSEKF Performance, Moderate Initial Uncertainty UT Austin March ‘ 11 31 of 35

BSEKF Performance, Large Initial Uncertainty UT Austin March ‘ 11 32 of 35

A PF Approximates the Probability Density Function as a Sum of Dirac Delta Functions GNC/Aug. ‘ 10 33 of 24

A Gaussian Sum Spreads the Component Functions & Can Achieve Better Accuracy GNC/Aug. ‘ 10 34 of 24

Summary & Conclusions n n n Developed novel navigation problem to illustrate challenges & opportunities of nonlinear estimation Reviewed estimation methods that extract/estimate internal states from sensor data Presented & evaluated 5 nonlinear estimation algorithms q q Examined Batch filter, EKF, UKF, PF, & BSEKF EKF, PF, & BSEKF have good performance for moderate initial errors Only BSEKF has good performance for large initial errors BSEKF has batch-like properties of insensitivity to initial estimates/guesses due to nonlinear least-squares optimization with algorithmic convergence guarantees UT Austin March ‘ 11 35 of 35
0af3ed49ec2b7c1ffbcbe95c1fe63578.ppt