c94a8b3ca6f2f0327eca5a289ef65a0e.ppt
- Количество слайдов: 24

Non-tree Routing for Reliability & Yield Improvement A. B. Kahng – UCSD B. Liu – Incentia I. I. Mandoiu – UCSD Work supported by Cadence, MARCO GSRC, and NSF

Outline l Motivation for non-tree routing l Problem formulation l Exact solution by integer programming l Greedy heuristic l Experimental results ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 2

Motivation for Redundant Interconnect l Manufacturing defects increasingly difficult to control in nanometer processes Ø Cannot expect continued decreases in defect density l Defects occur at Ø Ø Front end of the line (FEOL), i. e. , devices Back end of the line (BEOL), i. e. interconnect and vias l In nanometer processes BEOL defects are increasingly dominant Aluminum interconnects etched defect modality = short faults Ø Copper interconnects deposited defect modality = open faults Ø ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 3

Catastrophic Interconnect Faults Ø Open faults = missing material (or extra oxide where via should be formed) Ø Short faults = Extra material (or missing oxide) ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 4
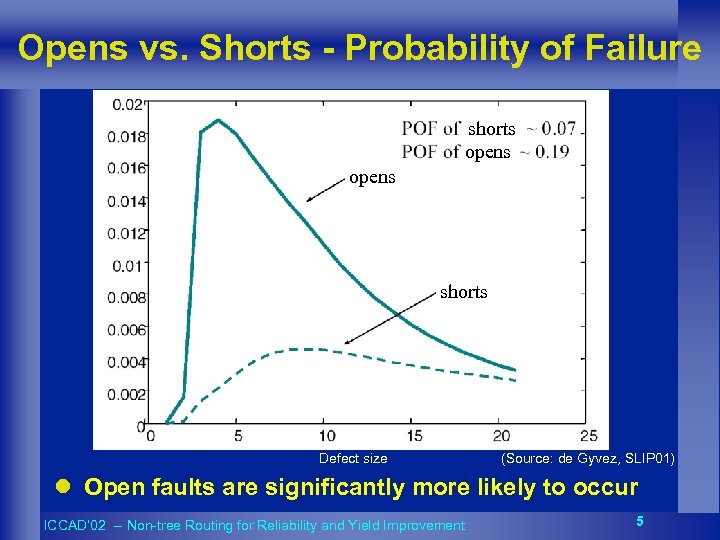
Opens vs. Shorts - Probability of Failure shorts opens shorts Defect size (Source: de Gyvez, SLIP 01) l Open faults are significantly more likely to occur ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 5

Opens vs. Shorts - Critical Area (CA) Shorts Opens (Source: de Gyvez, SLIP 01) Open fault CA larger than short fault CA ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 6

Reliability Improvement Approaches l Reduction of short critical area Conservative design rules Ø Decompaction Ø Effective in practice! Ø l Reduction of open critical area Wider wires Ø Non-tree interconnect Ø How effective? What are the tradeoffs involved? Ø l Related work Ø Ø [Mc. Coy-Robins 1995, Xue-Kuh 1995] non-tree interconnect for delay and skew reduction 2 -Edge-Connectivity Augmentation (E 2 AUG) ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 7

Our Contributions l Post-processing approach to non-tree routing for reliability improvement Ø Ø Ø One net at a time Easy to integrate in current flows Most appropriate for large non-critical nets l Compact integer program, practical up to 100 terminals l Faster, near-optimal greedy heuristic l Experimental study including comparison with best E 2 AUG heuristics and SPICE verification of delay and process variability ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 8

Problem Formulation Manhattan Routed Tree Augmentation (MRTA) Problem Given: Ø Tree T routed in the Manhattan plane Ø Feasible routing region FRR Ø Wirelength increase budget W Find: Ø Augmenting paths A within FRR Such that: Ø Total length of augmenting paths is less than W Ø Total length of biconnected edges in T A is maximum l Wirelength increase budget used to balance open CA decrease with short CA increase ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 9
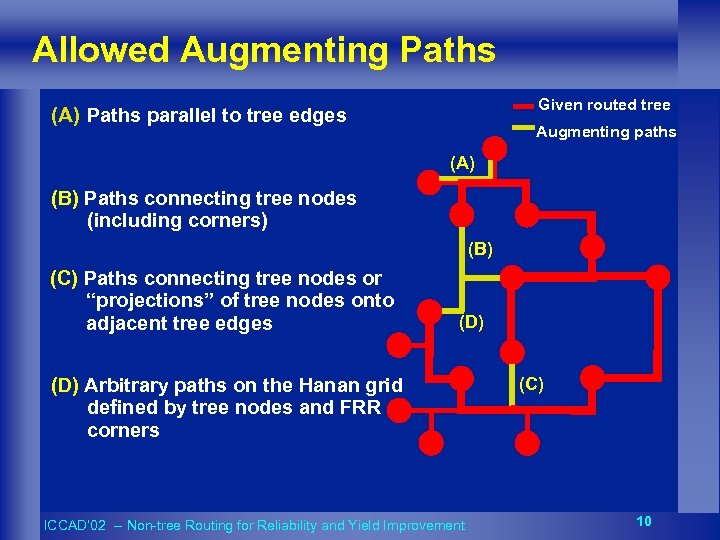
Allowed Augmenting Paths Given routed tree (A) Paths parallel to tree edges Augmenting paths (A) (B) Paths connecting tree nodes (including corners) (B) (C) Paths connecting tree nodes or “projections” of tree nodes onto adjacent tree edges (D) Arbitrary paths on the Hanan grid defined by tree nodes and FRR corners ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement (C) 10
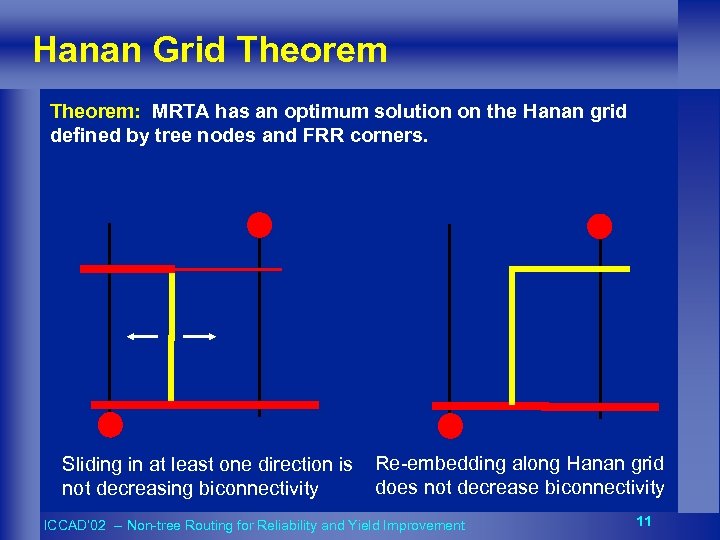
Hanan Grid Theorem: MRTA has an optimum solution on the Hanan grid defined by tree nodes and FRR corners. Sliding in at least one direction is not decreasing biconnectivity Re-embedding along Hanan grid does not decrease biconnectivity ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 11
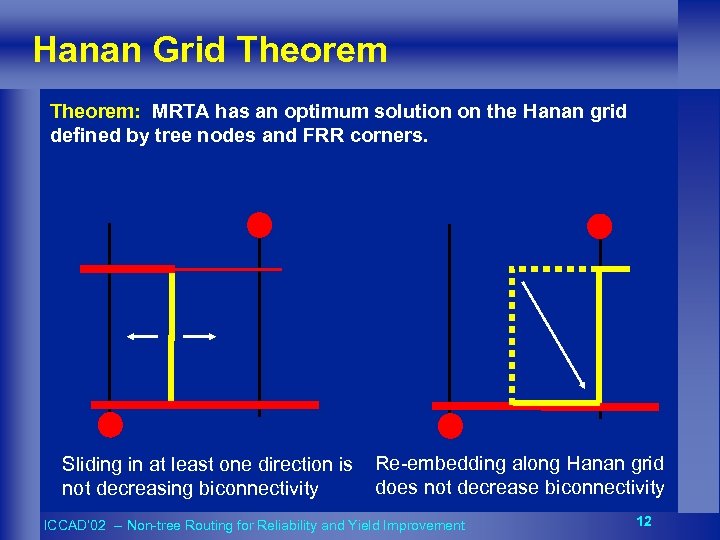
Hanan Grid Theorem: MRTA has an optimum solution on the Hanan grid defined by tree nodes and FRR corners. Sliding in at least one direction is not decreasing biconnectivity Re-embedding along Hanan grid does not decrease biconnectivity ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 12

MRTA vs. 2 -Edge-Connectivity Augmentation (E 2 AUG) Problem Given weighted graph G=(V, E) and spanning tree T, find minimum weight A E s. t. T A is 2 -edge-connected, i. e. , cannot be disconnected by removal of a single edge l E 2 AUG can be solved by performing binary search on WL increase budget of MRTA is NP-hard l Differences between MRTA and E 2 AUG Ø WL increase budget Ø Geometric context (Manhattan plane with obstacles) Ø “Partial” parallel edges Ø Steiner points (paths of type C and D) ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 13

Integer Linear Program (type A-C paths) Total biconnected length Subject to: Wirelength budget e biconnected if p connecting Tu & Tv {e|xe=1} gives augmenting paths {e|y e=1} gives biconnected tree edges l P = set of -- at most O(n 2) -- augmenting paths l WL budget is fully utilized by (implicit) parallel paths ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 14

Integer Linear Program (type D paths) Subject to l H = Hanan grid defined tree nodes and FRR corners l Exponentially many cut constraints Ø Fractional relaxation can still be solved using the ellipsoid algorithm ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 15

Greedy MRTA Algorithm Input : Routed tree T, wirelength budget W, feasible routing region, set V of allowed augmenting path endpoints Output: Augmented routing T A, with l(A) ≤ W 1. A = {}; mark all edges of T as bridges 2. Compute augmenting path lengths between every u, v V by |V| Dijkstra calls 3. Compute length of bridges on tree path between every u, v V by |V| DFS calls 4. Find path p with l(p) ≤ W and max ratio between length of bridges on the tree path between ends of p and l(p) 5. If ratio 1 then Ø Ø Add p to A Mark all edges on the tree path between ends of p as biconnected Update V and compute lengths for newly allowed paths (C type augmentation) Go to step 3 6. Else exit Runtime = O(N*D + K*N 2), reduced to O(K*N 2) w/o obstacles where N = #allowed endpoints, K = #added paths, D = Dijkstra runtime ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 16

Experimental Setup l Compared algorithms Ø Greedy Ø Integer program solved with CPLEX 7. 0 Ø Best-drop E 2 AUG heuristic [Khuller-Raghavachari-Zhu 99] v v Ø Uses min-weight branching to select best path to add and multiple restarts Modified to observe WL budget Recent E 2 AUG genetic algorithm [Raidl-Ljubic 2002] v Features compact edge-set representation + stochastic local improvement for solution space reduction l Test cases Ø WL increase budget = 1%, 2%, 5%, 10%, 20%, no limit Ø Net size between 5 and 1000 terminals v v Ø Random nets routed using BOI heuristic Min-area and timing driven nets extracted from real designs No routing obstacles ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 17
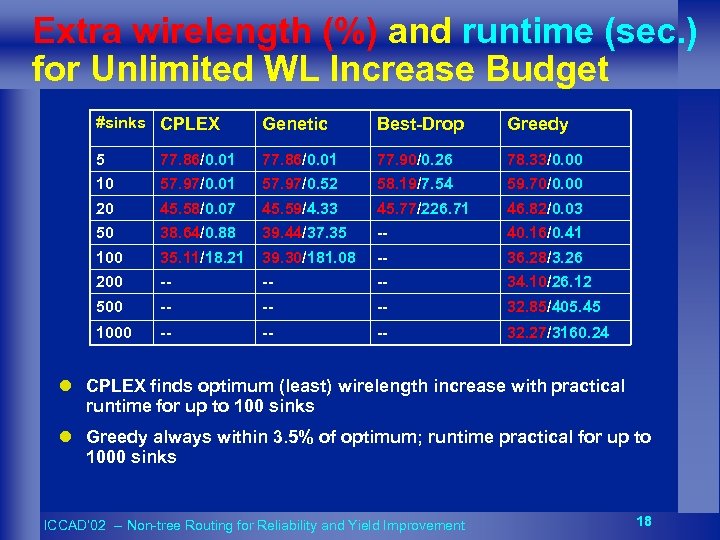
Extra wirelength (%) and runtime (sec. ) for Unlimited WL Increase Budget #sinks CPLEX Genetic Best-Drop Greedy 5 77. 86/0. 01 77. 90/0. 26 78. 33/0. 00 10 57. 97/0. 01 57. 97/0. 52 58. 19/7. 54 59. 70/0. 00 20 45. 58/0. 07 45. 59/4. 33 45. 77/226. 71 46. 82/0. 03 50 38. 64/0. 88 39. 44/37. 35 -- 40. 16/0. 41 100 35. 11/18. 21 39. 30/181. 08 -- 36. 28/3. 26 200 -- -- -- 34. 10/26. 12 500 -- -- -- 32. 85/405. 45 1000 -- -- -- 32. 27/3160. 24 l CPLEX finds optimum (least) wirelength increase with practical runtime for up to 100 sinks l Greedy always within 3. 5% of optimum; runtime practical for up to 1000 sinks ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 18
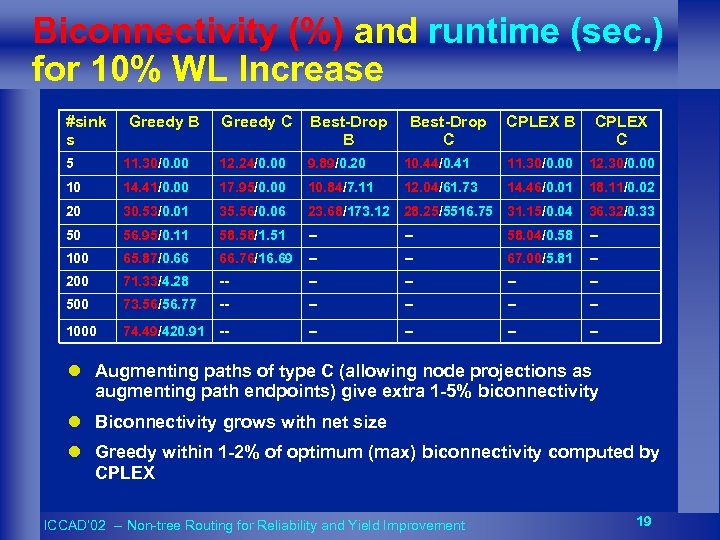
Biconnectivity (%) and runtime (sec. ) for 10% WL Increase #sink s Greedy B Greedy C Best-Drop B Best-Drop C CPLEX B CPLEX C 5 11. 30/0. 00 12. 24/0. 00 9. 89/0. 20 10. 44/0. 41 11. 30/0. 00 12. 30/0. 00 10 14. 41/0. 00 17. 95/0. 00 10. 84/7. 11 12. 04/61. 73 14. 46/0. 01 18. 11/0. 02 20 30. 53/0. 01 35. 56/0. 06 23. 68/173. 12 28. 25/5516. 75 31. 15/0. 04 36. 32/0. 33 50 56. 95/0. 11 58. 58/1. 51 -- -- 58. 04/0. 58 -- 100 65. 87/0. 66 66. 76/16. 69 -- -- 67. 00/5. 81 -- 200 71. 33/4. 28 -- -- -- 500 73. 56/56. 77 -- -- -- 1000 74. 49/420. 91 -- -- -- l Augmenting paths of type C (allowing node projections as augmenting path endpoints) give extra 1 -5% biconnectivity l Biconnectivity grows with net size l Greedy within 1 -2% of optimum (max) biconnectivity computed by CPLEX ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 19
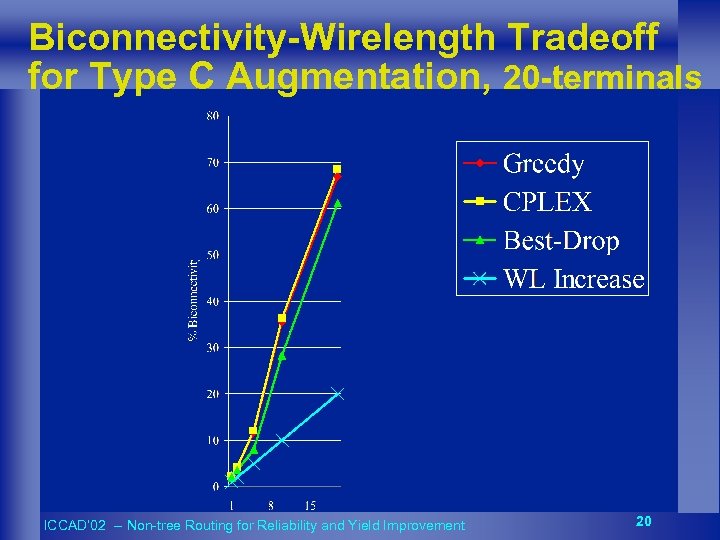
Biconnectivity-Wirelength Tradeoff for Type C Augmentation, 20 -terminals ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 20
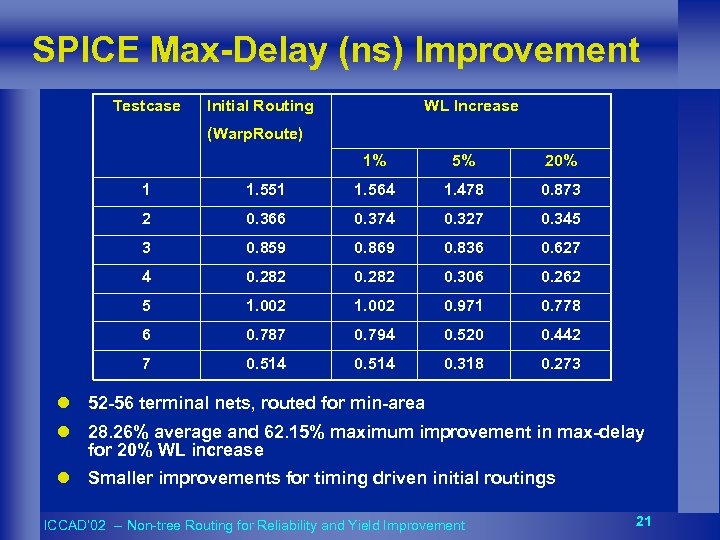
SPICE Max-Delay (ns) Improvement Testcase Initial Routing WL Increase (Warp. Route) 1% 5% 20% 1 1. 551 1. 564 1. 478 0. 873 2 0. 366 0. 374 0. 327 0. 345 3 0. 859 0. 869 0. 836 0. 627 4 0. 282 0. 306 0. 262 5 1. 002 0. 971 0. 778 6 0. 787 0. 794 0. 520 0. 442 7 0. 514 0. 318 0. 273 l 52 -56 terminal nets, routed for min-area l 28. 26% average and 62. 15% maximum improvement in max-delay for 20% WL increase l Smaller improvements for timing driven initial routings ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 21

Process Variability Robustness Testcase Initial Routing (Warp. Route) 20% WL Increase 1 1. 551± 4. 126% 0. 873± 3. 780% 2 0. 366± 3. 552% 0. 345± 2. 898% 3 0. 859± 3. 958% 0. 627± 3. 668% 4 0. 282± 2. 837% 0. 262± 3. 053% 5 1. 002± 3. 792% 0. 778± 3. 470% 6 0. 787± 3. 812% 0. 442± 3. 167% 7 0. 514± 3. 502% 0. 273± 2. 930% l Width w=w 0, w 0± 6. 67% l Delay variation computed as (maxw d(w) – minw d(w)) / d(w 0) l 13. 79% average and 28. 86% maximum reduction in delay variation for 20% WL increase ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 22

Summary l Post-processing tree augmentation approach to reliability and manufacturing yield improvement Ø Results show significant biconnectivity increase with small increase in wirelength, especially for large nets l. Future work includes ØMultiple net augmentation ØSimultaneous non-tree augmentation & decompaction ØConsideration of defect-size distribution ØReliability with timing constraints ICCAD’ 02 -- Non-tree Routing for Reliability and Yield Improvement 23

Thank You!
c94a8b3ca6f2f0327eca5a289ef65a0e.ppt