Non-linear Regression Analysis with Fitter Software Application Alexey

Non-linear Regression Analysis with Fitter Software Application Alexey Pomerantsev Semenov Institute of Chemical Physics Russian Chemometrics Society 12. 02 1

Agenda 1. Introduction 2. TGA Example 3. NLR Basics 4. Multicollinearity 5. Prediction 6. Testing 7. Bayesian Estimation 8. Conclusions 12. 02 2

1. Introduction 12. 02 3

Linear and Non-linear Regressions Linear Non Linear f=a exp(-20 x) f=exp(-ax) Formula Example Source Choice Dimension Soft Close relatives? Multicollinearity Interpretation Purpose Soft Tools 12. 02 Hard Easy ? Large Difficult ? Small Excess of parameters Well-known Interpolation Many Lack of data Uncommon Extrapolation Few 4

2. Thermo Gravimetric Analysis Example Object Goal PVC Cable Isolation Let’s see it! Service-Life Prediction Experiment Thermo Gravimetric Method Tool Non-Linear Regression and Fitter 12. 02 5

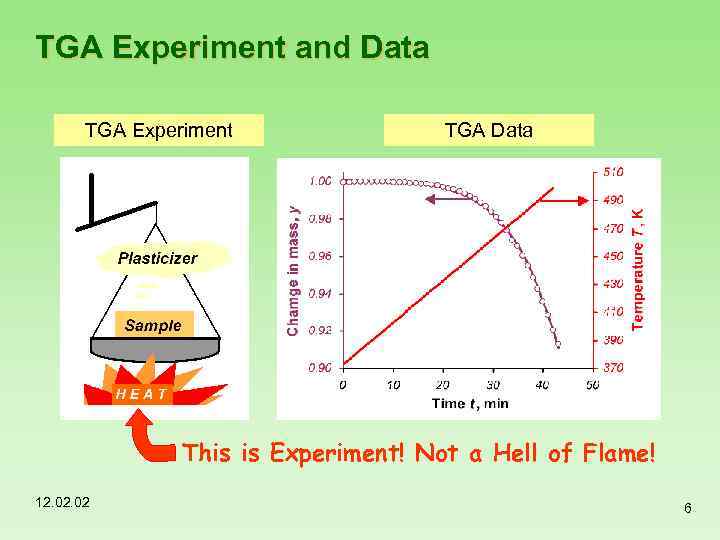TGA Experiment and Data TGA Experiment TGA Data This is Experiment! Not a Hell of Flame! 12. 02 6

TGA Example Variables Estimated Measured Intermediate Response y=m/m 0 Change in mass Predictors t Time C Plasticizer concentration Small size problem! Parameters y 0 Initial value of y C 0 Initial concentration k 0 Evaporation rate constant v T 0 Heating rate E Activation energy F Sample specific surface 12. 02 Initial temperature 7

Plasticizer Evaporation Model Evaporation Law Diffusion is not relevant! Volume Change The Arrhenius law Temperature growth 12. 02 8

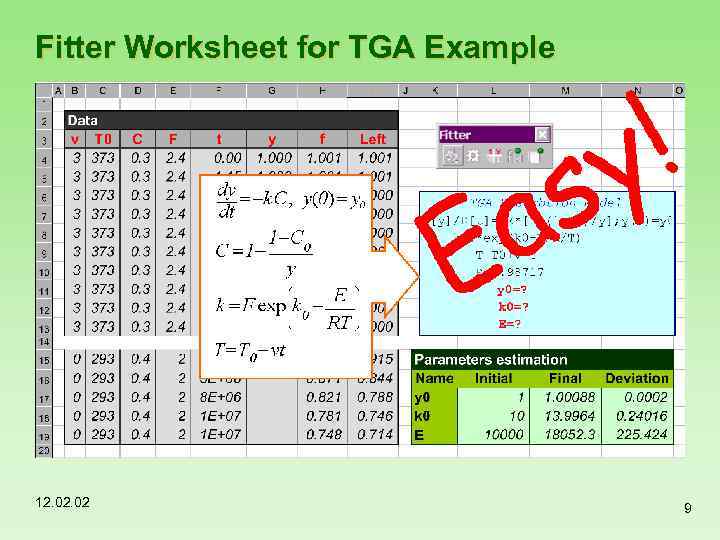Fitter Worksheet for TGA Example 12. 02 9

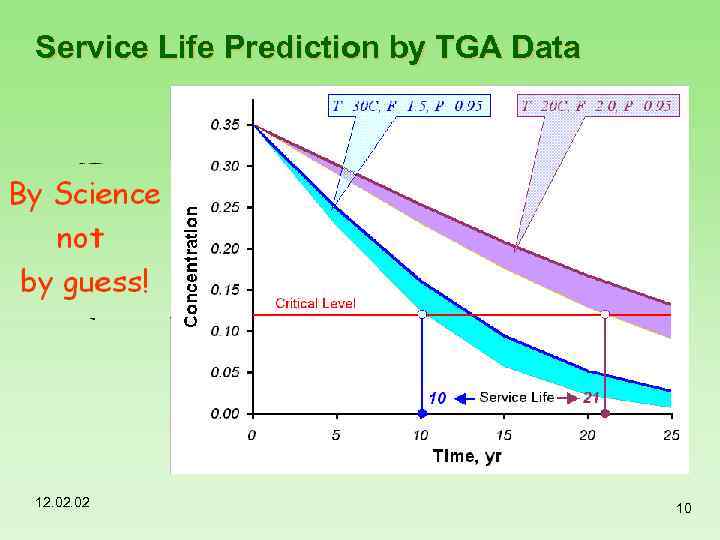Service Life Prediction by TGA Data 12. 02 10

3. NLR Basics 12. 02 11

Data and Errors Response Predictors Weights Parameters Fit Weight is an effective instrument! Absolute error Weight and variance Relative error 12. 02 12

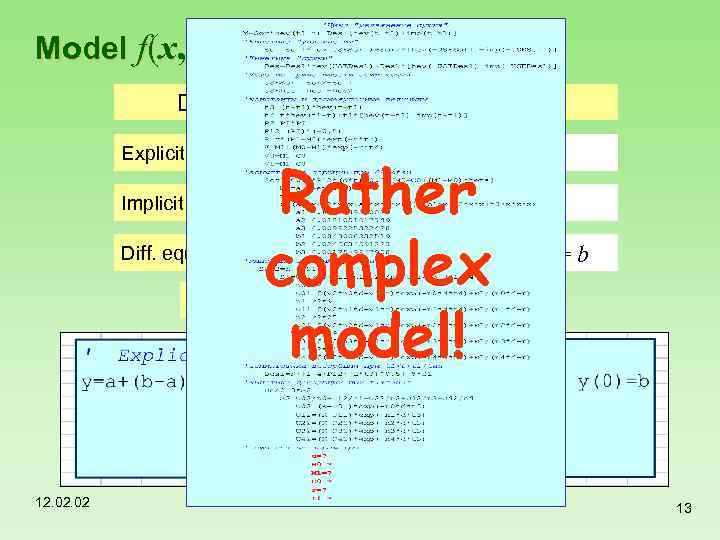Model f(x, a) Different shapes of the same model Explicit model Implicit model Diff. equation y = a + (b – a)*exp(–c*x) Rather complex model! 0 = a + (b – a)*exp(–c*x) – y d[y]/d[x] = – c*(y –a); y(0) = b Presentation at worksheet 12. 02 13

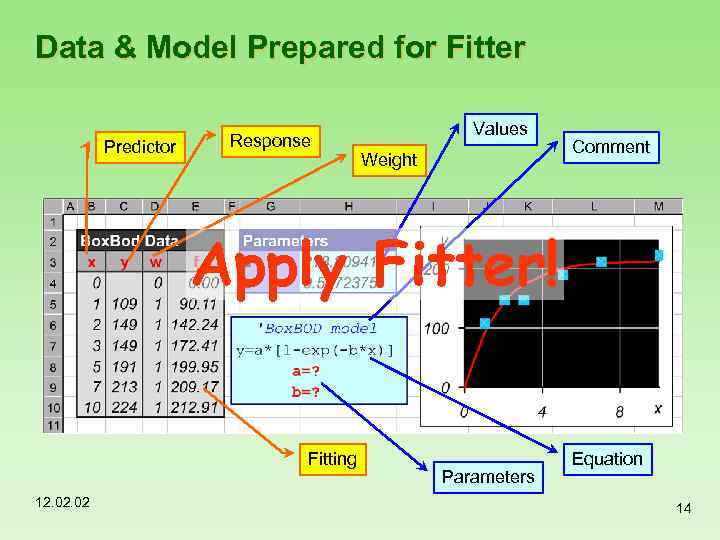Data & Model Prepared for Fitter Predictor Response Values Weight Comment Apply Fitter! Fitting 12. 02 Parameters Equation 14

Objective Function Q(a) Sum of squares Objective function Q is a sum of squares and may be more… Bayesian term Objective function Parameter estimates 12. 02 Weighted variance estimate 15

Very Important Matrix A Hesse’s matrix Gauss’ approximation Matrix A is the cause of troubles. . Model derivatives Covariance matrix F-matrix 12. 02 16

Quality of Estimation Covariances Matrix Deviations Vector Matrix A is the measure of quality! Correlations Matrix Final Objective Value Error Variance and Number Degrees of Freedom 12. 02 17

Search by Gradient Method Matrix A is the key to search! a Search problems Initial point 0 Local minima 12. 02 18

4. Multicollinearity 12. 02 19

Multicollinearity: View Multicollinearity is degradation of matrix A Objective function Q(a) Spread of eigenvalues is a measure of degradation N(A) = 1 7 6 5 4 2 12. 02 20

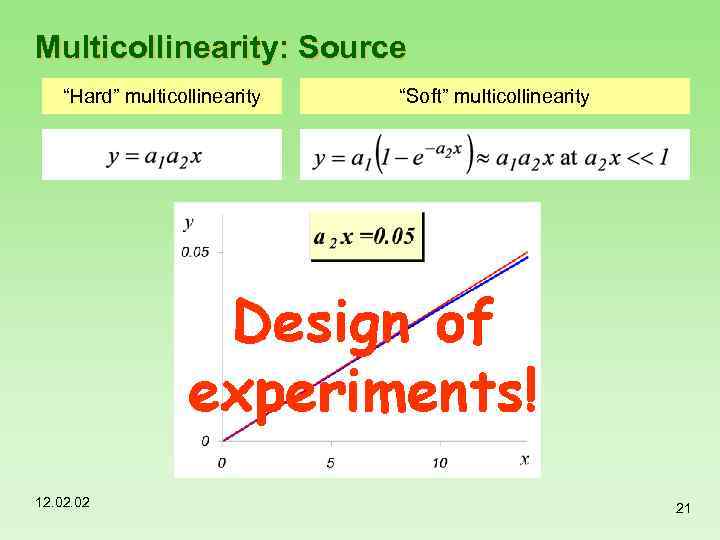Multicollinearity: Source “Hard” multicollinearity 12. 02 “Soft” multicollinearity 21

Data & Model Preprocessing ((a + b) + c) + d a + (b + (c + d)) as 1+10 – 20 = 1 Representation of a number in computer with 64 bits 1 0 0 1 … 0 1 1 Target is to make Hesse matrix A regular and decrease N(A) M e a n s 12. 02 X m. X Data Scaling X X – X 0 Data Centering Model Adjusting a (a) x (x) y (y) 22

Example: The Arrhenius Law Standard form Adjusted form Scaling & centering Adjusting k 10+11 E 10+4 N(A) = 20 12. 02 a 1 1 a 2 10 N(A) = 2 23

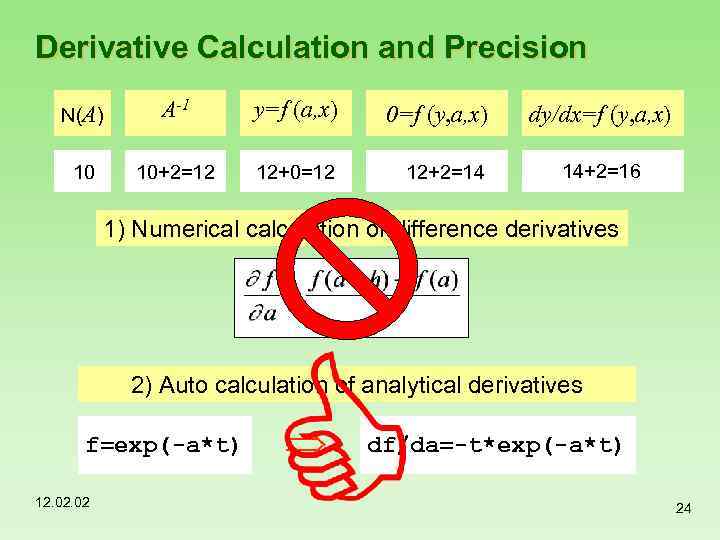Derivative Calculation and Precision N(A) A-1 y=f (a, x) 0=f (y, a, x) dy/dx=f (y, a, x) 6 10 8 6+2=8 10+2=12 8+2=10 8+0=8 12+0=12 10+0=10 8+2=10 10+2=12 12+2=14 14+2=16 10+2=12 12+2=14 1) Numerical calculation of difference derivatives 2) Auto calculation of analytical derivatives f=exp(-a*t) 12. 02 df/da=-t*exp(-a*t) 24

5. Prediction 12. 02 25

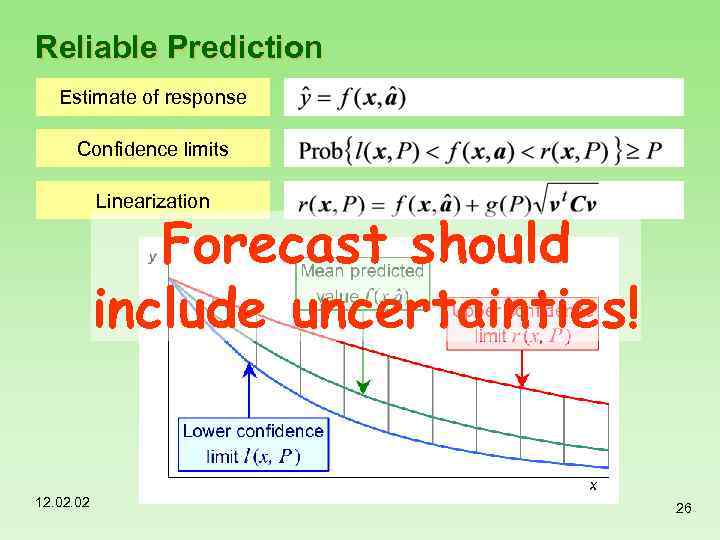Reliable Prediction Estimate of response Confidence limits Linearization Forecast should include uncertainties! 12. 02 26

Nonlinearity and Simulation Non-linear models call for special methods of reliable prediction! 12. 02 27

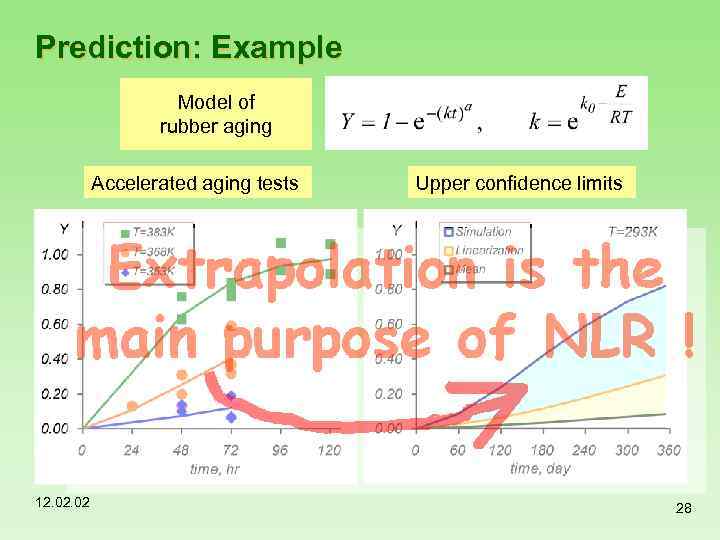Prediction: Example Model of rubber aging Accelerated aging tests 12. 02 Upper confidence limits 28

6. Testing 12. 02 29

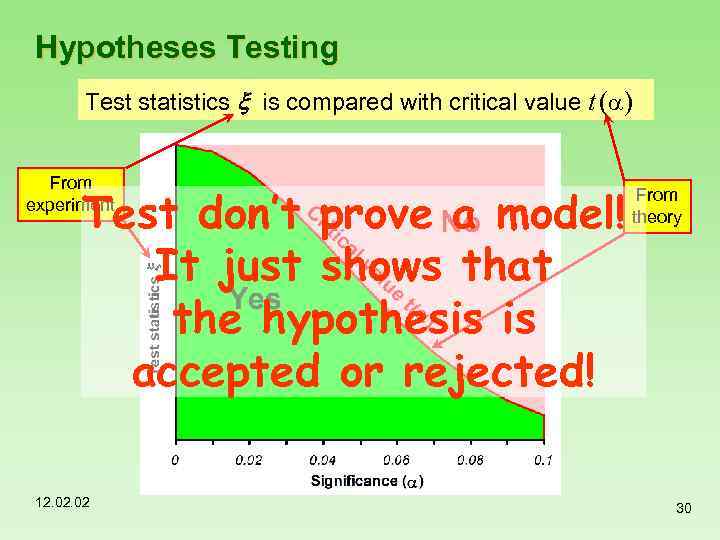Hypotheses Testing Test statistics x is compared with critical value t (a) From experiment Test don’t prove a model! It just shows that the hypothesis is accepted or rejected! 12. 02 From theory 30

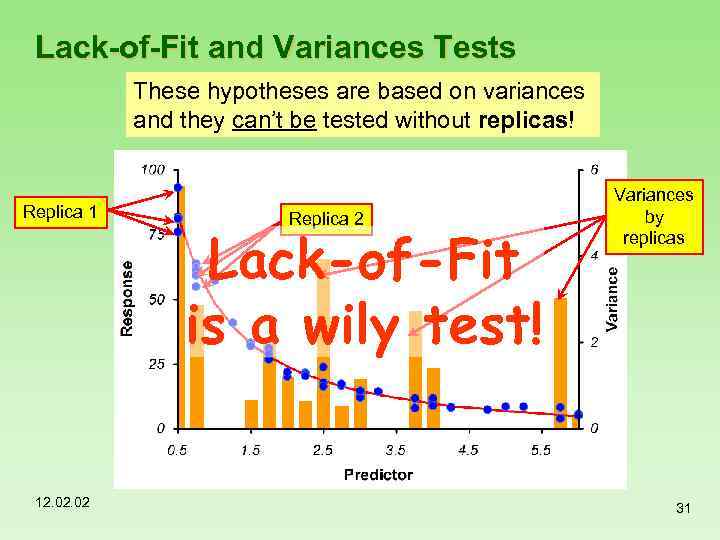Lack-of-Fit and Variances Tests These hypotheses are based on variances and they can’t be tested without replicas! Replica 1 12. 02 Replica 2 Lack-of-Fit is a wily test! Variances by replicas 31

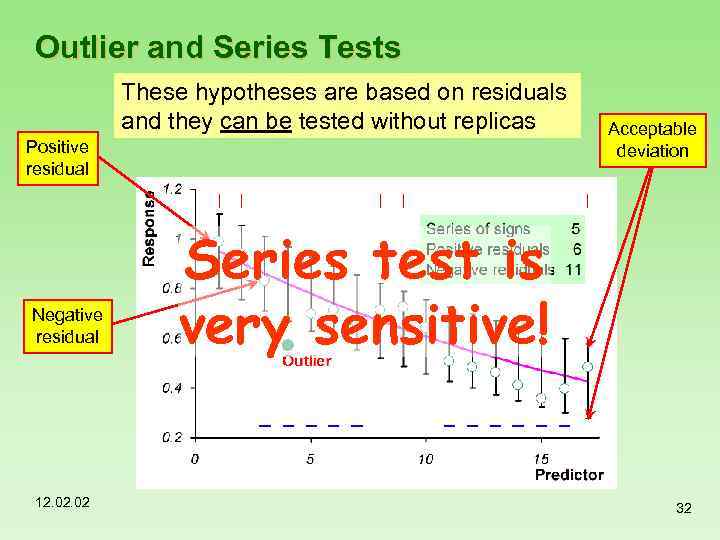Outlier and Series Tests These hypotheses are based on residuals and they can be tested without replicas Positive residual Negative residual 12. 02 Acceptable deviation Series test is very sensitive! 32

7. Bayesian Estimation 12. 02 33

Bayesian Estimation How to eat away an elephant? Slice by slice! 12. 02 34

Posterior and Prior Information. Type I Posterior Information Parameter estimates Prior parameter values b Matrix F Recalculated matrix H Error variance s 2 Prior variance value NDF Prior NDF The same error sin N N each portion of data! f 2 0 0 Objective Function 12. 02 35

Posterior and Prior Information. Type II Posterior Information Parameter estimates Prior parameter values b Matrix F Recalculated matrix H Different errors in each portion of data! Objective Function 12. 02 36

8. Conclusions Mysterious Nature LR Model NLR Model Thank you! 12. 02 37