Non-Hierarchical Sequencing Graphs Algorithmic Graph Theory 2

Скачать презентацию Non-Hierarchical Sequencing Graphs Algorithmic Graph Theory 2

3ff7cb4950fcfd7e5f7daeb80fbc3bb4.ppt

Количество слайдов: 98

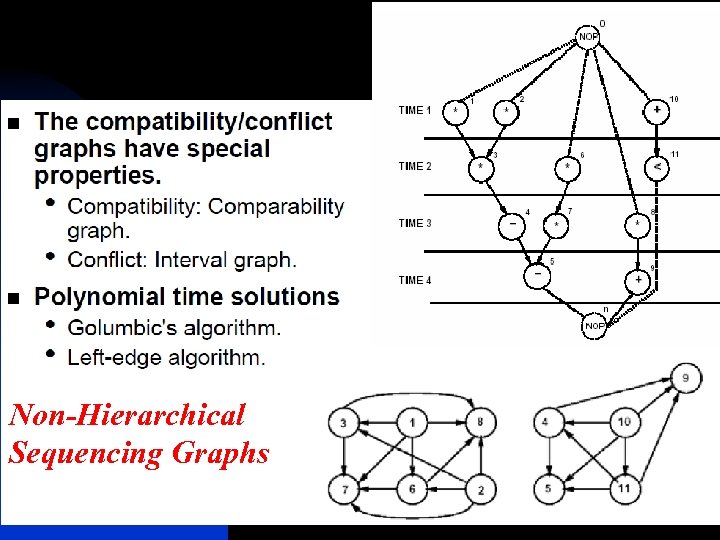Non-Hierarchical Sequencing Graphs

Algorithmic Graph Theory 2

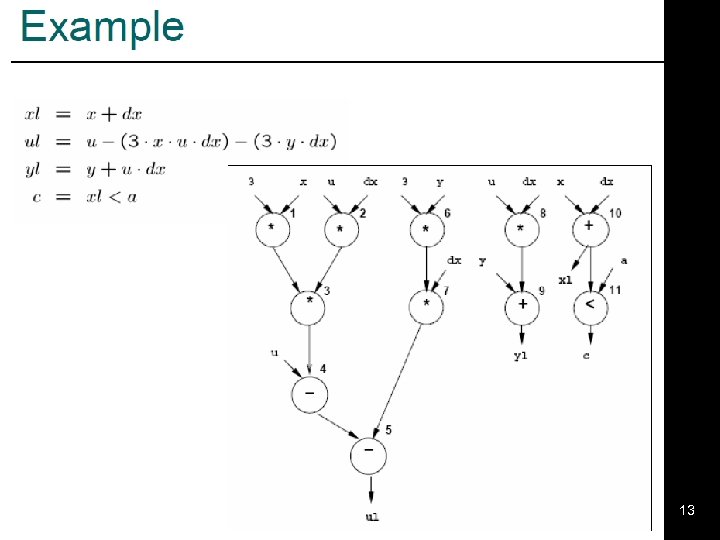
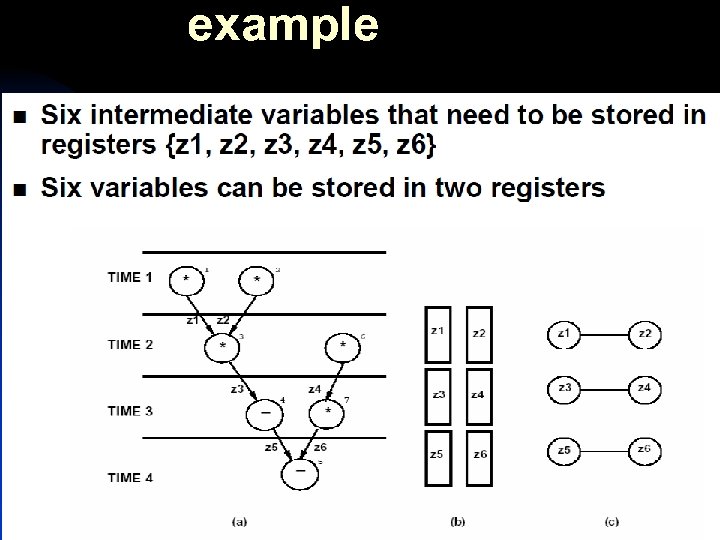example Algorithmic Graph Theory 3

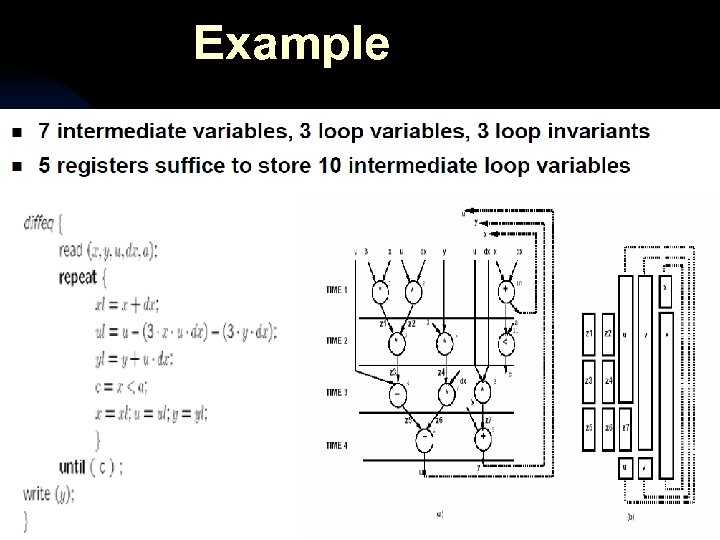Example Algorithmic Graph Theory 4

Algorithmic Graph Theory 5

Algorithmic Graph Theory 6

Algorithmic Graph Theory 7

Algorithmic Graph Theory 8

Algorithmic Graph Theory 9

Algorithmic Graph Theory 10

Algorithmic Graph Theory 11

Algorithmic Graph Theory 12

Algorithmic Graph Theory 13

Algorithmic Graph Theory 14

Algorithmic Graph Theory 15

Algorithmic Graph Theory 16

Algorithmic Graph Theory 17

Algorithmic Graph Theory 18

Algorithmic Graph Theory 19

Algorithmic Graph Theory 20

Algorithmic Graph Theory 21

Algorithmic Graph Theory 22

Algorithmic Graph Theory 23

Algorithmic Graph Theory 24

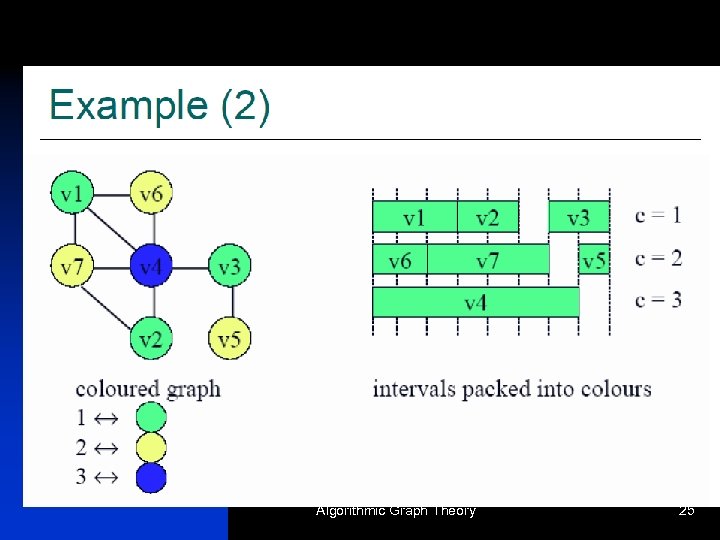Algorithmic Graph Theory 25

Algorithmic Graph Theory 26

Algorithmic Graph Theory and its Applications Martin Charles Golumbic Algorithmic Graph Theory 32

Algorithmic Graph Theory and its Applications Martin Charles Golumbic Algorithmic Graph Theory 33

Algorithmic Graph Theory and its Applications Martin Charles Golumbic Algorithmic Graph Theory 34

Introduction n n n Intersection Graphs Interval Graphs Greedy Coloring The Berge Mystery Story Other Structure Families of Graphs Graph Sandwich Problems Probe Graphs and Tolerance Graphs Algorithmic Graph Theory 35

The concept of an intersection graph n n n applications in computation operations research molecular biology scheduling designing circuits rich mathematical problems Algorithmic Graph Theory 36

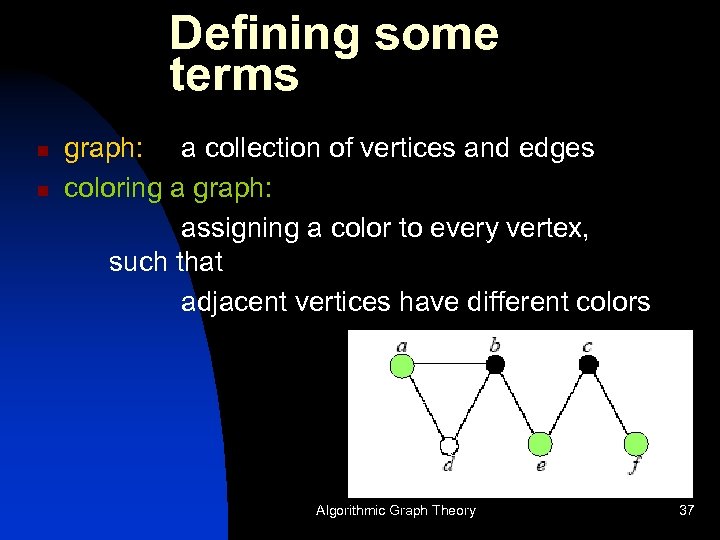Defining some terms n n graph: a collection of vertices and edges coloring a graph: assigning a color to every vertex, such that adjacent vertices have different colors Algorithmic Graph Theory 37

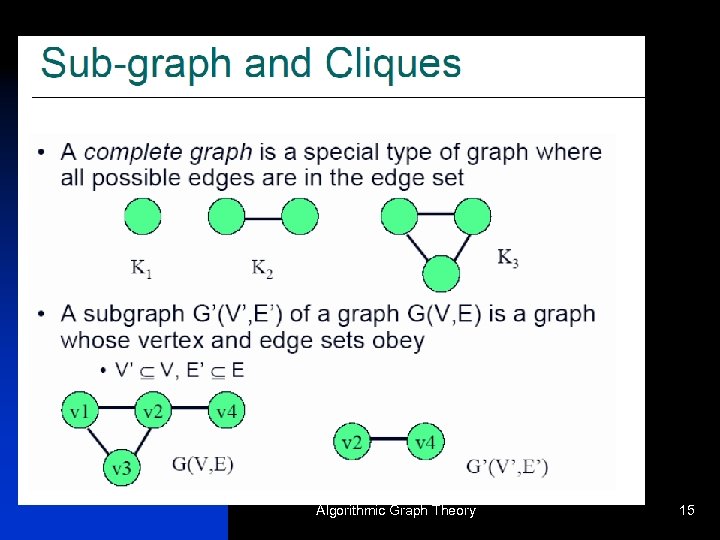
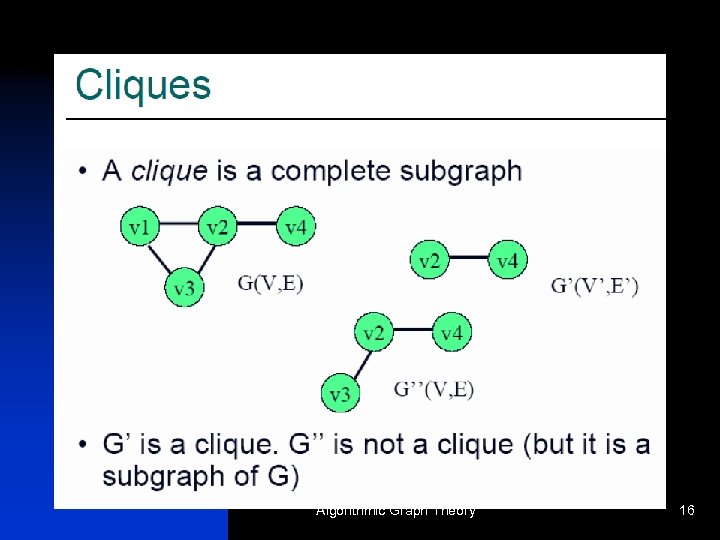
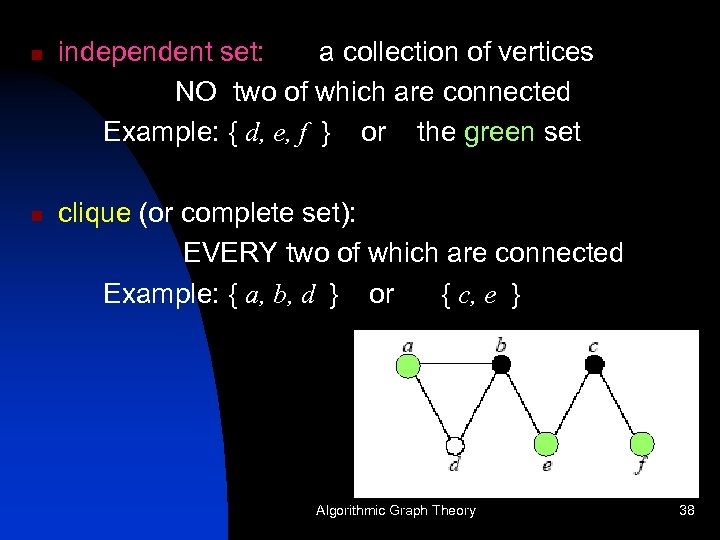n n independent set: a collection of vertices NO two of which are connected Example: { d, e, f } or the green set clique (or complete set): EVERY two of which are connected Example: { a, b, d } or { c, e } Algorithmic Graph Theory 38

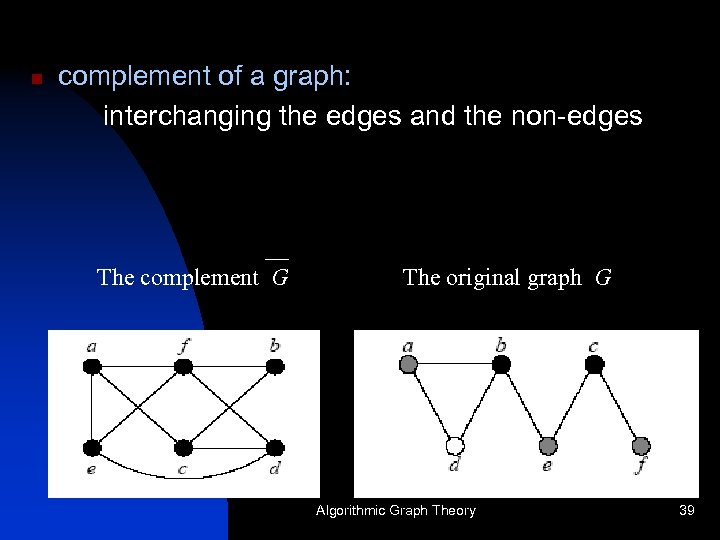n complement of a graph: interchanging the edges and the non-edges __ The complement G The original graph G Algorithmic Graph Theory 39

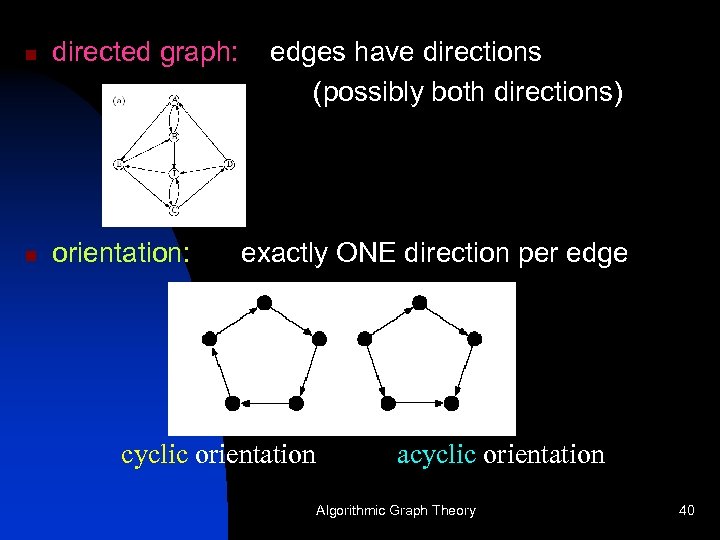n directed graph: n orientation: edges have directions (possibly both directions) exactly ONE direction per edge cyclic orientation acyclic orientation Algorithmic Graph Theory 40

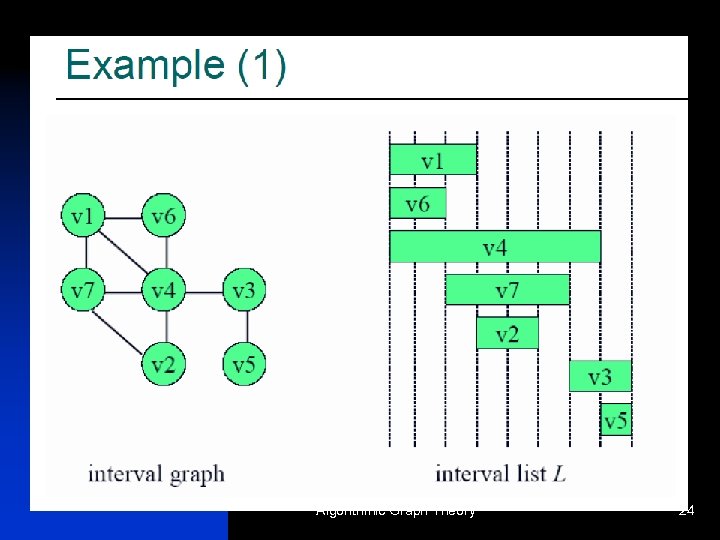
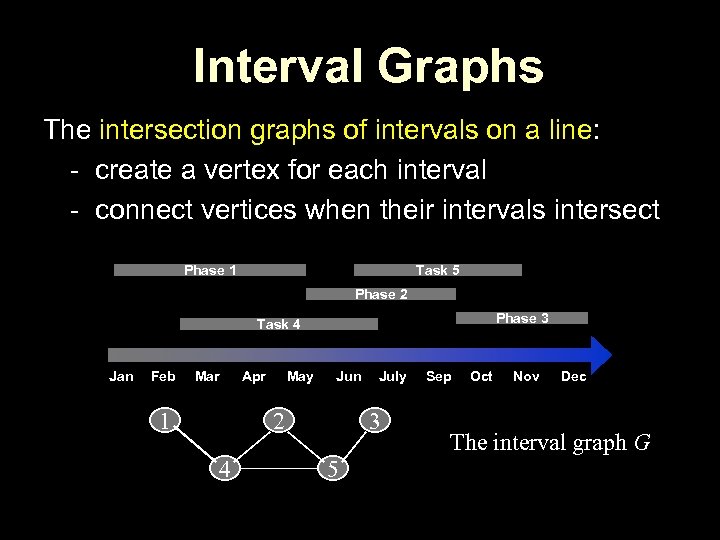Interval Graphs The intersection graphs of intervals on a line: - create a vertex for each interval - connect vertices when their intervals intersect Phase 1 Task 5 Phase 2 Phase 3 Task 4 Jan Feb Mar 1 Apr May Jun 2 4 July 3 5 Sep Oct Nov Dec The interval graph G

History of Interval Graphs n n n Hajos 1957: Combinatorics (scheduling) Benzer 1959: Biology (genetics) Gilmore & Hoffman 1964: Characterization Booth & Lueker 1976: First linear time recognition algorithm Many other applications: mobile radio frequency assignment VLSI design temporal reasoning in AI computer storage allocation Algorithmic Graph Theory 42

Scheduling Example n Lectures need to be assigned classrooms at the University. Lecture #a: 9: 00 -10: 15 u Lecture #b: 10: 00 -12: 00 u etc. u n n Conflicting lectures Different rooms How many rooms?

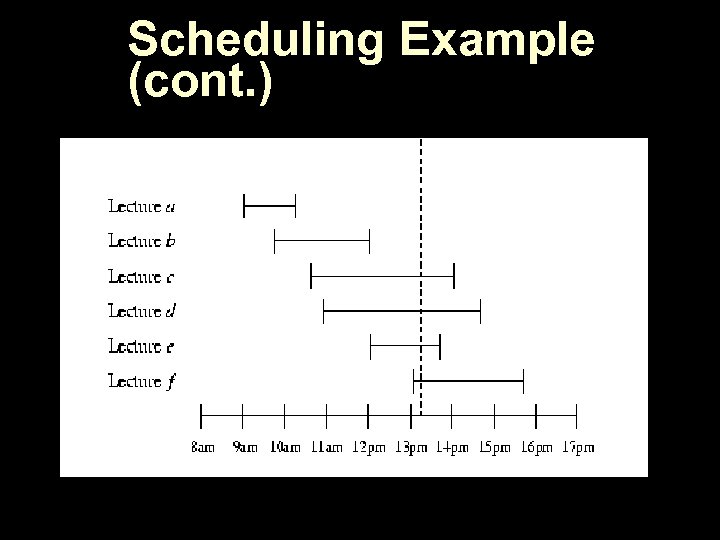Scheduling Example (cont. )

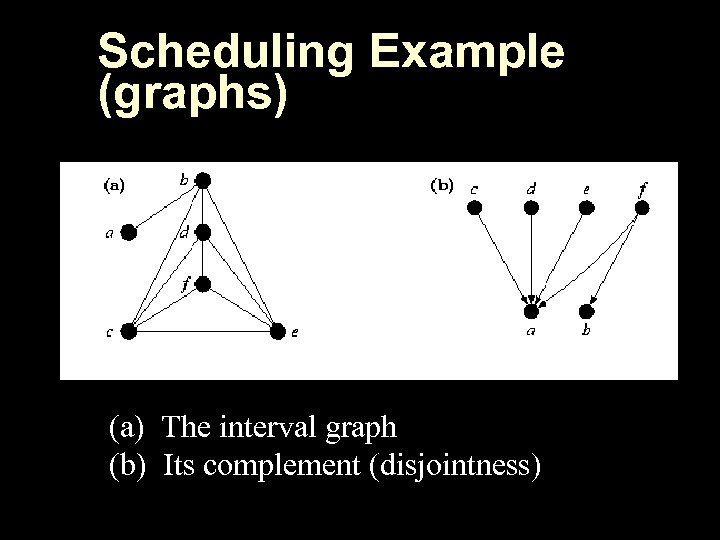Scheduling Example (graphs) (a) The interval graph (b) Its complement (disjointness)

Coloring Interval Graphs n n n interval graphs have special properties used to color them efficiently coloring algorithm sweeps across from left to right assigning colors in a ``greedy manner” This is optimal ! Algorithmic Graph Theory 46

Coloring Interval Graphs Algorithmic Graph Theory 47

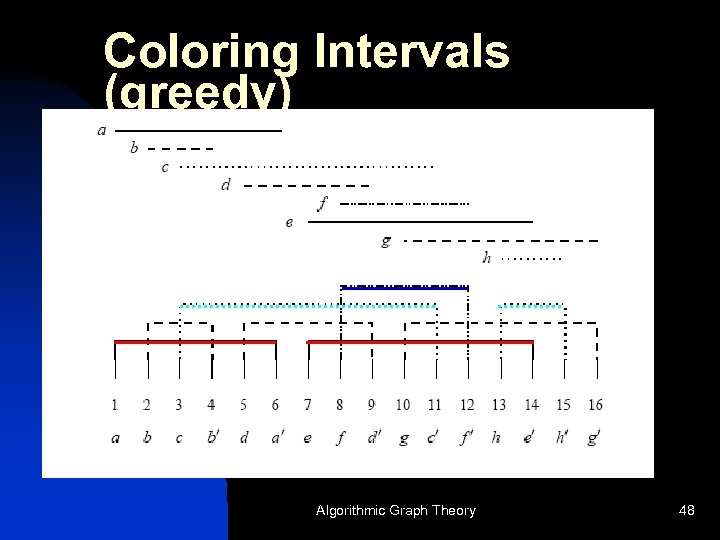Coloring Intervals (greedy) Algorithmic Graph Theory 48

Is greedy the best we can do? n n Can we prove optimality? Yes: It uses the smallest # colors. Proof: Let k be the number of colors used. Look at the point P, when color k was used first. At P all the colors 1 to k-1 were busy! We are forced to use k colors at P. And, they form a clique of size k in the interval graph. Algorithmic Graph Theory 49

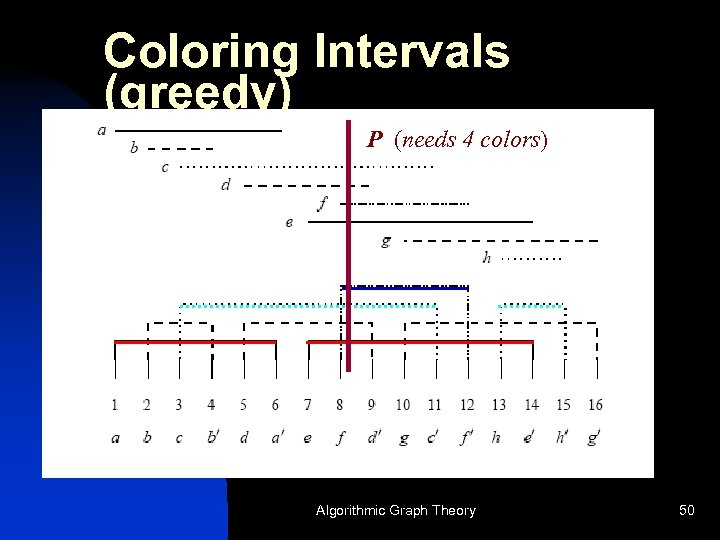Coloring Intervals (greedy) P (needs 4 colors) Algorithmic Graph Theory 50

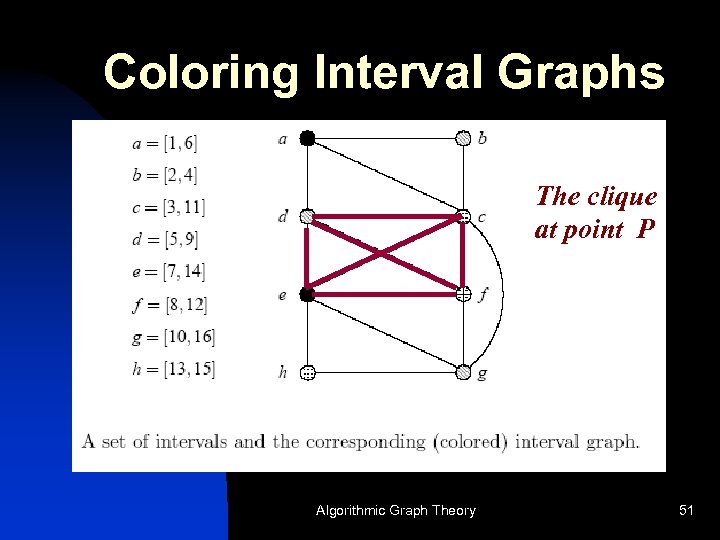Coloring Interval Graphs The clique at point P Algorithmic Graph Theory 51

Greedy the best we can do ! Formally, (1) at least k colors are required (because of the clique) (2) greedy succeeded using k colors. Therefore, the solution is optimal. Algorithmic Graph Theory Q. E. D. 52

Characterizing Interval Graphs n n n Properties of interval graphs How to recognize them Their mathematical structure Algorithmic Graph Theory 53

Characterizing Interval Graphs n n n Properties of interval graphs How to recognize them Their mathematical structure Two properties characterize interval graphs: - The Chordal Graph Property - The co-TRO Property Algorithmic Graph Theory 54

The Chordal Graph Property chordal graph: every cycle of length > 4 has a chord (connecting two vertices that are not consecutive) i. e. , they may not contain chordless cycles! Algorithmic Graph Theory 55

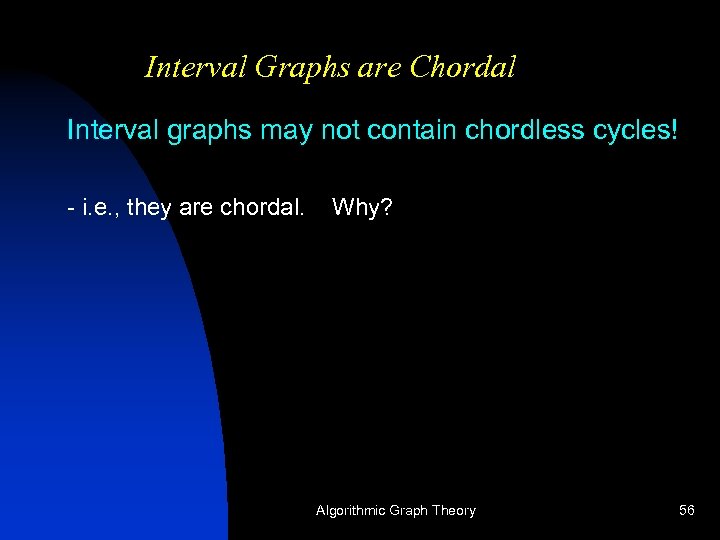Interval Graphs are Chordal Interval graphs may not contain chordless cycles! - i. e. , they are chordal. Why? Algorithmic Graph Theory 56

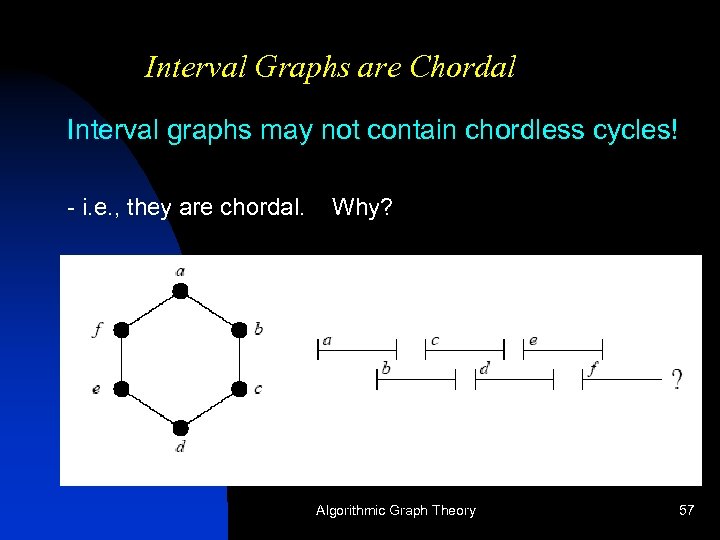Interval Graphs are Chordal Interval graphs may not contain chordless cycles! - i. e. , they are chordal. Why? Algorithmic Graph Theory 57

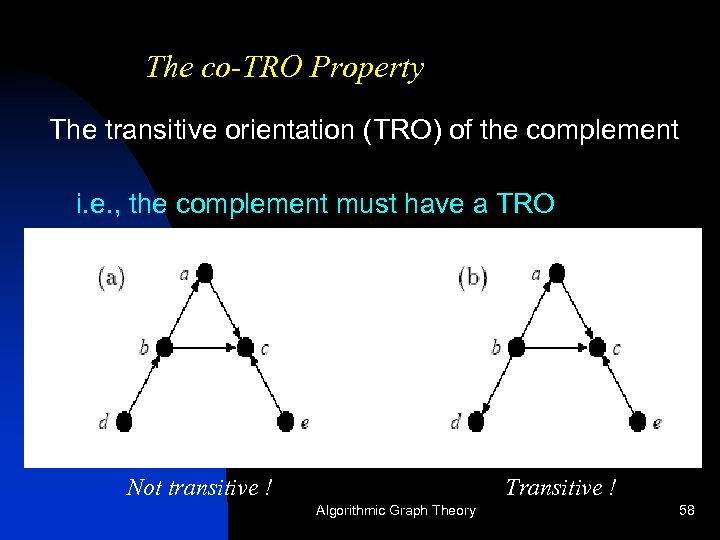The co-TRO Property The transitive orientation (TRO) of the complement i. e. , the complement must have a TRO Not transitive ! Transitive ! Algorithmic Graph Theory 58

Interval Graphs are co-TRO The complement of an Interval graph has a transitive orientation! - Why? The complement is the disjointness graph. So, orient from the earlier interval to the later interval. Algorithmic Graph Theory 59

Gilmore and Hoffman (1964) Theorem: A graph G is an interval graph if and only if__ Is chordal and G its complement G is transitively orientable. This provides the basis for the first set of recognition algorithms in the early 1970’s. Algorithmic Graph Theory 60

A Mystery in the Library The Berge Mystery Story: Six professors had been to the library on the day that the rare tractate was stolen. Each had entered once, stayed for some time and then left. If two were in the library at the same time, then at least one of them saw the other. Detectives questioned the professors and gathered the following testimony:

The Facts: n n n Abe said that he saw Burt and Eddie Burt reported that he saw Abe and Ida Charlotte claimed to have seen Desmond and Ida Desmond said that he saw Abe and Ida Eddie testified to seeing Burt and Charlotte Ida said that she saw Charlotte and Eddie One of the Professor LIED !! Who was it?

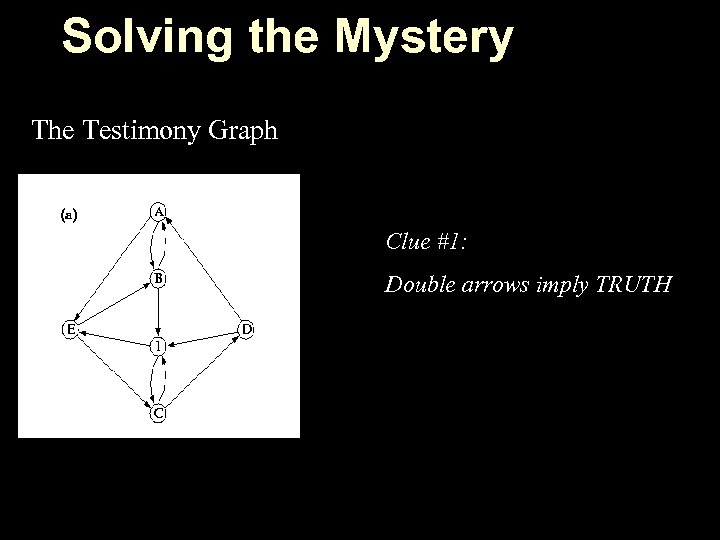Solving the Mystery The Testimony Graph Clue #1: Double arrows imply TRUTH

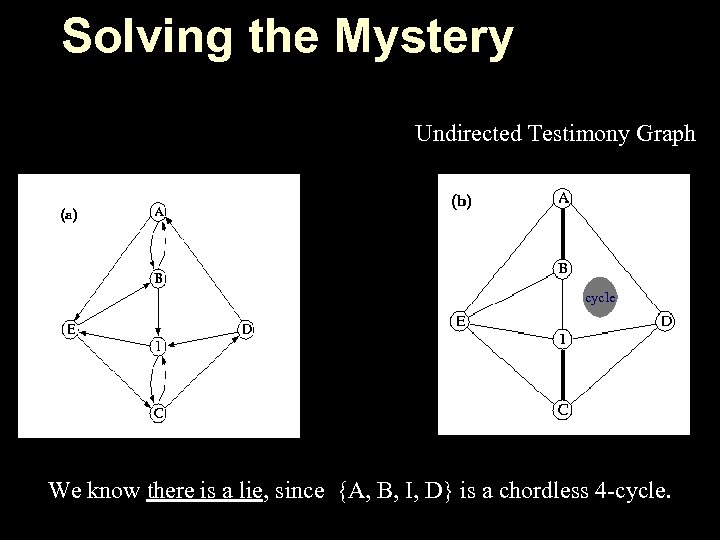Solving the Mystery Undirected Testimony Graph cycle We know there is a lie, since {A, B, I, D} is a chordless 4 -cycle.

Intersecting Intervals cannot form Chordless Cycles Burt Desmond Abe No place for Ida’s interval: It must hit both B and D but cannot hit A. Impossible!

Solving the Mystery One professor from the chordless 4 -cycle must be a liar. There are three chordless 4 -cycles: {A, B, I, D} {A, D, I, E} {A, E, C, D} Burt is NOT a liar: He is missing from the second cycle. Ida is NOT a liar: She is missing from the third cycle. Charlotte is NOT a liar: She is missing from the second. Eddie is NOT a liar: He is missing from the first cycle. WHO IS THE LIAR? Abe or Desmond ?

Solving the Mystery (cont. ) WHO IS THE LIAR? Abe or Desmond ? If Abe were the liar and Desmond truthful, then {A, B, I, D} would remain a chordless 4 -cycle, since B and I are truthful. Therefore: Desmond is the liar.

Was Desmond Stupid or Just Ignorant? If Desmond had studied algorithmic graph theory, he would have known that his testimony to the police would not hold up. Algorithmic Graph Theory 68

Many other Families of Intersection Graphs Victor Klee, in a paper in 1969: ``What are the intersection graphs of arcs in a circle? ’’ Algorithmic Graph Theory 69

Many other Families of Intersection Graphs Victor Klee, in a paper in 1969: ``What are the intersection graphs of arcs in a circle? “ Algorithmic Graph Theory 70

Many other Families of Intersection Graphs Victor Klee, in a paper in 1969: ``What are the intersection graphs of arcs in a circle? “ Klee’s paper was an implicit challenge - consider a whole variety of problems - on many kinds of intersection graphs. Algorithmic Graph Theory 71

Families of Intersection Graphs n n n boxes in the plane paths in a tree chords of a circle spheres in 3 -space trapezoids, parallelograms, curves of functions many other geometrical and topological bodies The Algorithmic Problems: – – recognize them color them find maximum cliques find maximum independent sets Algorithmic Graph Theory 73

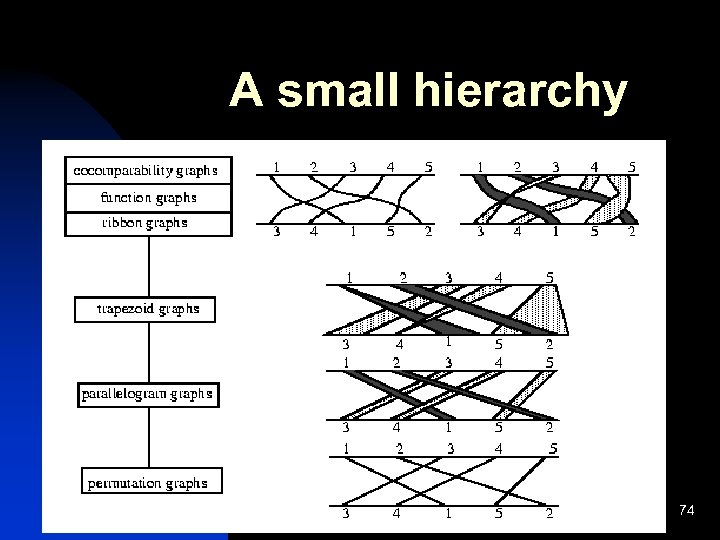A small hierarchy Algorithmic Graph Theory 74

The Story Begins Bell Labs in New Jersey (Spring 1981) John Klincewicz: Suppose you are routing phone calls in a tree network. Two calls interfere if they share an edge of the tree. How can you optimally schedule the calls? An Olive Tree Network • A call is a path between a pair of nodes. • A typical example of a type of intersection graph. • Intersection here means “share an edge”. • Coloring this intersection graph is scheduling the calls. Algorithmic Graph Theory 77

Edge Intersection Graphs of Paths in a Tree (EPT graphs) n n tree communication network connecting different places if two of these paths overlap, they conflict and cannot use the same resource at the same time. n Two types of intersections – share an edge vs share a node Algorithmic Graph Theory 78

EPT graphs EPT graph share an edge Algorithmic Graph Theory 79

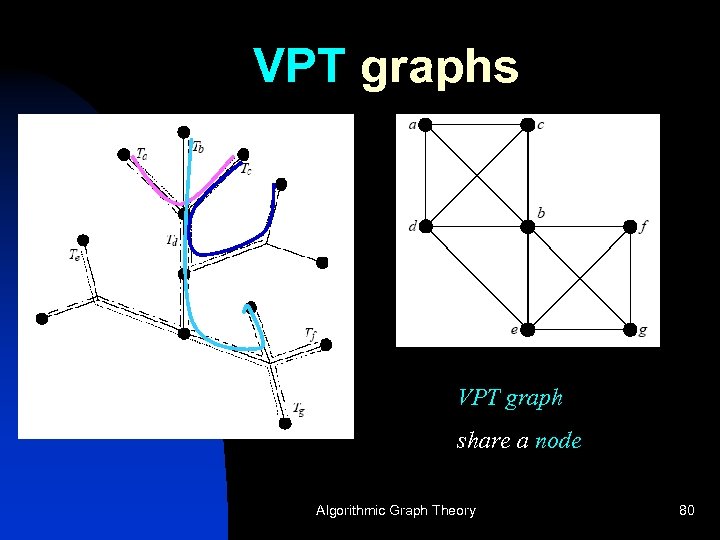VPT graphs VPT graph share a node Algorithmic Graph Theory 80

Some Interesting Theorems n n VPT graphs are chordal EPT graphs are NOT chordal Algorithmic Graph Theory 81

Some Interesting Theorems VPT graphs are chordal n n Buneman, Gavril, Wallace (early 1970's) G is the vertex intersection graph of subtrees of a tree if and only if it is a chordal graph. Mc. Morris & Shier (1983) A graph G is a vertex intersection graph of distinct subtrees of a star if and only if both G and its complement are chordal. Algorithmic Graph Theory 82

Some Interesting Theorems EPT graphs are NOT chordal An EPT representation of C 6 1 6 called a “ 6 -pie”. 2 5 4 3 Chordless cycles have a unique EPT representation. Algorithmic Graph Theory 83

Algorithmic Complexity Results Algorithmic Graph Theory 84

Some Interesting Theorems n Folklore (1970’s) Every graph G is the edge intersection graph of distinct subtrees of a star. Algorithmic Graph Theory 85

Degree 3 host trees (continued) Theorem (1985): All four classes are equivalent: chordal EPT deg 3 EPT VPT EPT deg 3 VPT What about degree 4? Algorithmic Graph Theory 86

Degree 3 host trees (continued) Theorem (1985): All four classes are equivalent: chordal EPT deg 3 EPT VPT EPT deg 3 VPT Degree 4 host trees Theorem (2005) [Golumbic, Lipshteyn, Stern]: weakly chordal EPT deg 4 EPT Algorithmic Graph Theory 87

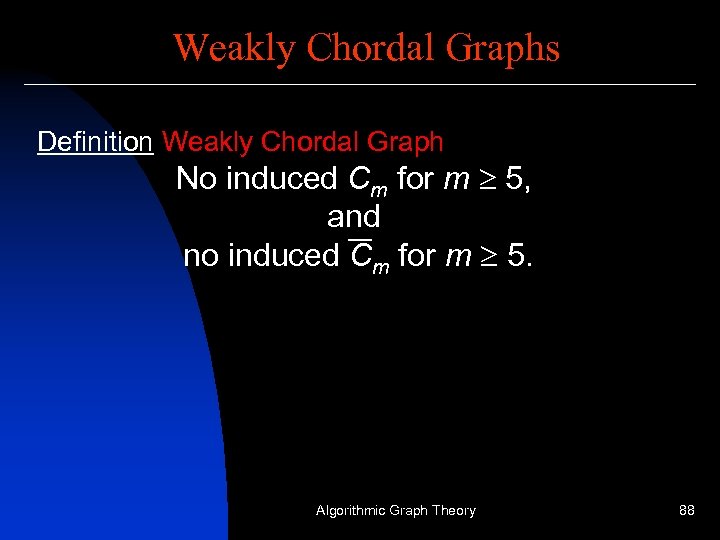Weakly Chordal Graphs Definition Weakly Chordal Graph No induced Cm for m 5, and no induced Cm for m 5. Algorithmic Graph Theory 88

The Story Continues Algorithmic Graph Theory 89

The Interval Graph Sandwich Problem n n Interval problems with missing edges Benzer’s original problem partial intersection data u Is it consistent ? u n n Complete data would be recognition interval graphs (polynomial) Partial data needs a different model and is NP-complete Algorithmic Graph Theory 90

Interval Graph Sandwich Problem n given a partially specified graph E 1 u E 2 u E 3 u n n required edges optional edges forbidden edges Can you fill-in some of the optional edges, so that the result will be an interval graph? Golumbic & Shamir (1993): NP-Complete Algorithmic Graph Theory 91

Interval Probe Graphs n A special tractable case of interval sandwich Computational biology motivated n Interval probe graph: vertices are partitioned n P probes & N non-probes (independent set) u can fill-in some of the N x N edges, u so that the result will be an interval graph n Motivation Algorithmic Graph Theory 92

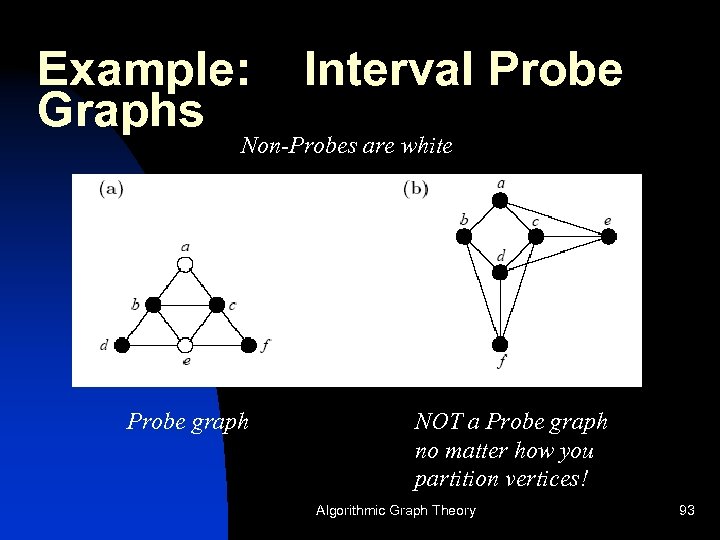Example: Graphs Interval Probe Non-Probes are white Probe graph NOT a Probe graph no matter how you partition vertices! Algorithmic Graph Theory 93

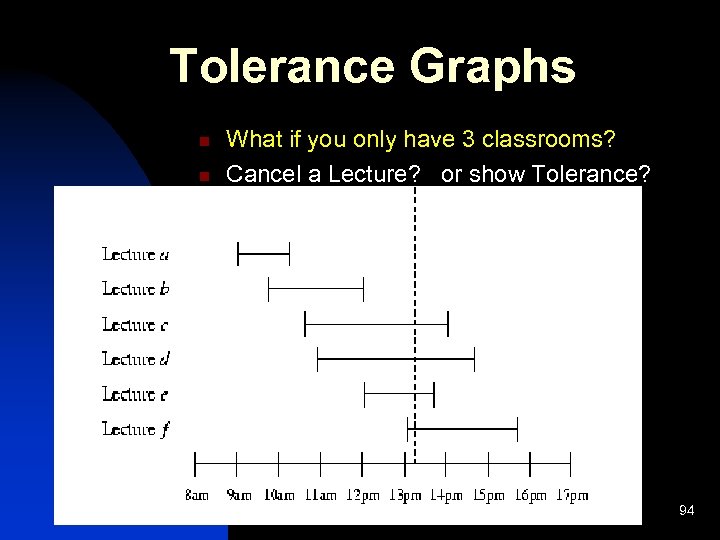Tolerance Graphs n n What if you only have 3 classrooms? Cancel a Lecture? or show Tolerance? Algorithmic Graph Theory 94

Tolerance Graphs Measured intersection: small, or ``tolerable’’ amount of overlap, may be ignored does NOT produce an edge at least one of them has to be ``bothered’’ Algorithmic Graph Theory 95

Tolerance Graphs Measured intersection: small, or ``tolerable’’ amount of overlap, may be ignored does NOT produce an edge at least one of them has to be ``bothered’’ n Assignment of positive numbers {tv} (v V) such that vw E if and only if | Iv Iw | min {tv , tw} Algorithmic Graph Theory 96

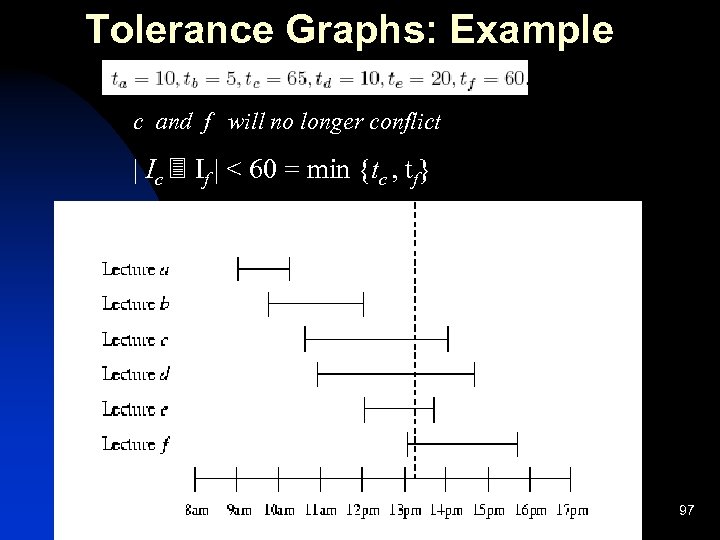Tolerance Graphs: Example c and f will no longer conflict | Ic If | < 60 = min {tc , tf} Algorithmic Graph Theory 97