Скачать презентацию Non-compartmental analysis and The Mean Residence Time approach Скачать презентацию Non-compartmental analysis and The Mean Residence Time approach

9a1c07a4c50eca390a2f60e28eca2cea.ppt

  • Количество слайдов: 47

Non-compartmental analysis and The Mean Residence Time approach A Bousquet-Mélou 1 Non-compartmental analysis and The Mean Residence Time approach A Bousquet-Mélou 1

Synonymous Mean Residence Time approach Statistical Moment Approach Non-compartmental analysis 2 Synonymous Mean Residence Time approach Statistical Moment Approach Non-compartmental analysis 2

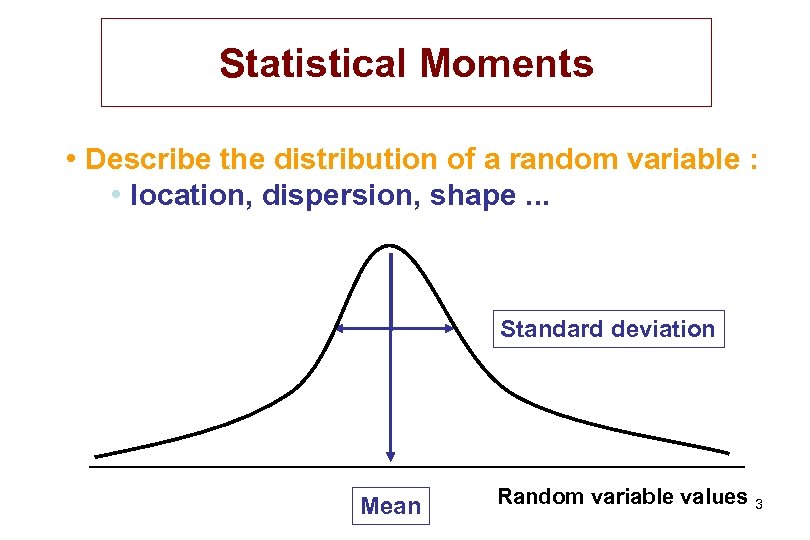Statistical Moments • Describe the distribution of a random variable : • location, dispersion, Statistical Moments • Describe the distribution of a random variable : • location, dispersion, shape. . . Standard deviation Mean Random variable values 3

Statistical Moment Approach Stochastic interpretation of drug disposition • Individual particles are considered : Statistical Moment Approach Stochastic interpretation of drug disposition • Individual particles are considered : they are assumed to move independently accross kinetic spaces according to fixed transfert probabilities • The time spent in the system by each particule is considered as a random variable • The statistical moments are used to describe the distribution of this random variable, and more generally the behaviour of drug particules in the system 4

Statistical Moment Approach • n-order statistical moment • zero-order : • one-order : 5 Statistical Moment Approach • n-order statistical moment • zero-order : • one-order : 5

Statistical Moment Approach Statistical moments in pharmacokinetics. J Pharmacokinet Biopharm. 1978 Dec; 6(6): 547 Statistical Moment Approach Statistical moments in pharmacokinetics. J Pharmacokinet Biopharm. 1978 Dec; 6(6): 547 -58. Yamaoka K, Nakagawa T, Uno T. Statistical moments in pharmacokinetics: models and assumptions. J Pharmacol. 1993 Oct; 45(10): 871 -5. Dunne A. 6

The Mean Residence Time 7 The Mean Residence Time 7

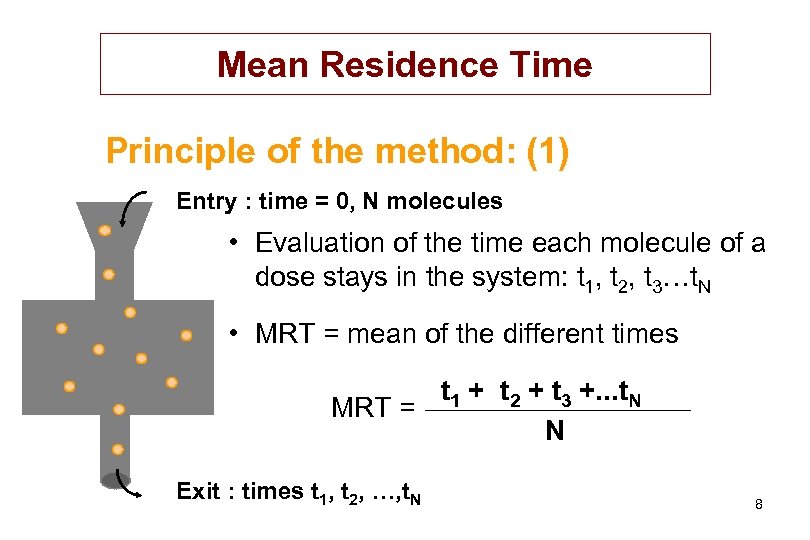Mean Residence Time Principle of the method: (1) Entry : time = 0, N Mean Residence Time Principle of the method: (1) Entry : time = 0, N molecules • Evaluation of the time each molecule of a dose stays in the system: t 1, t 2, t 3…t. N • MRT = mean of the different times t 1 + t 2 + t 3 +. . . t. N MRT = N Exit : times t 1, t 2, …, t. N 8

Mean Residence Time Principle of the method : (2) • Under minimal assumptions, the Mean Residence Time Principle of the method : (2) • Under minimal assumptions, the plasma concentration curve provides information on the time spent by the drug molecules in the body 9

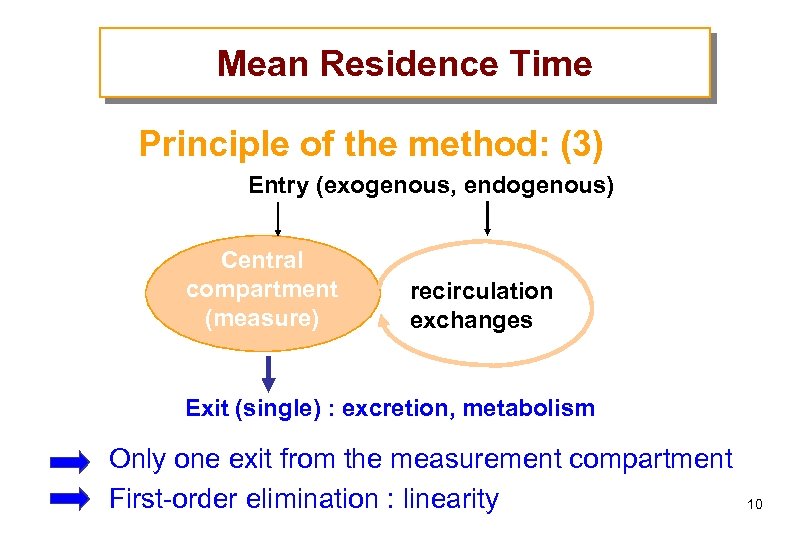Mean Residence Time Principle of the method: (3) Entry (exogenous, endogenous) Central compartment (measure) Mean Residence Time Principle of the method: (3) Entry (exogenous, endogenous) Central compartment (measure) recirculation exchanges Exit (single) : excretion, metabolism Only one exit from the measurement compartment First-order elimination : linearity 10

Mean Residence Time Principle of the method: (4) • N molecules administered in the Mean Residence Time Principle of the method: (4) • N molecules administered in the system at t=0 • The molecules eliminated at t 1 have a residence time in the system equal to t 1 Consequence of linearity • AUCtot is proportional to N C • Number n 1 of molecules eliminated at t 1+ t is proportional to AUC t: C 1 n 1 = t 1 (t) AUC t AUCtot XN = C(t 1) x t AUCtot XN 11

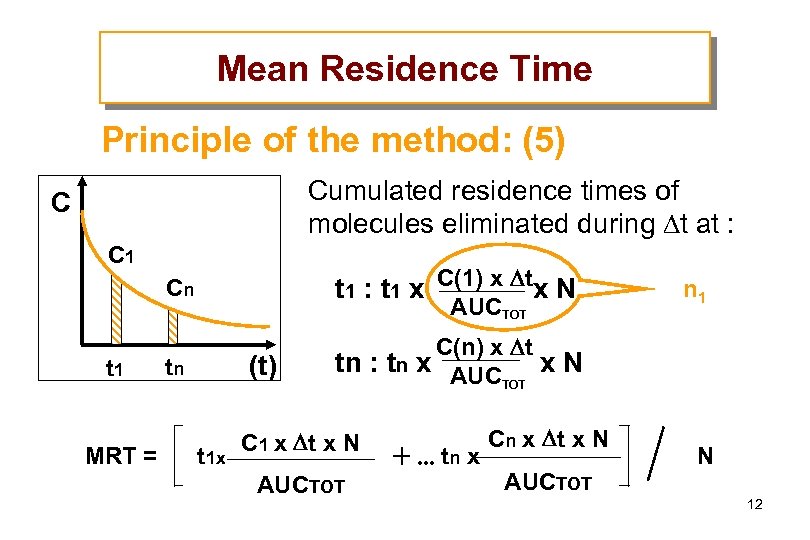Mean Residence Time Principle of the method: (5) Cumulated residence times of molecules eliminated Mean Residence Time Principle of the method: (5) Cumulated residence times of molecules eliminated during t at : C C 1 Cn t 1 MRT = t 1 : t 1 x C(1) x tx N tn C(n) x t tn : tn x AUC x N TOT AUCTOT (t) C 1 x t x N n 1 Cn x t x N t 1 x tn x N AUCTOT 12

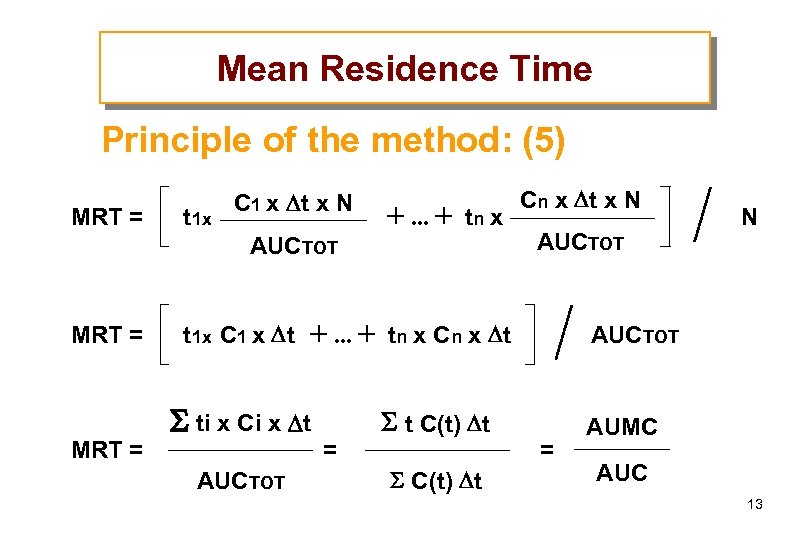Mean Residence Time Principle of the method: (5) Cn x t x N C Mean Residence Time Principle of the method: (5) Cn x t x N C 1 x t x N MRT = t 1 x tn x N AUCTOT MRT = t 1 x C 1 x t tn x Cn x t MRT = ti x Ci x t AUCTOT = t C(t) t AUCTOT = AUMC AUC 13

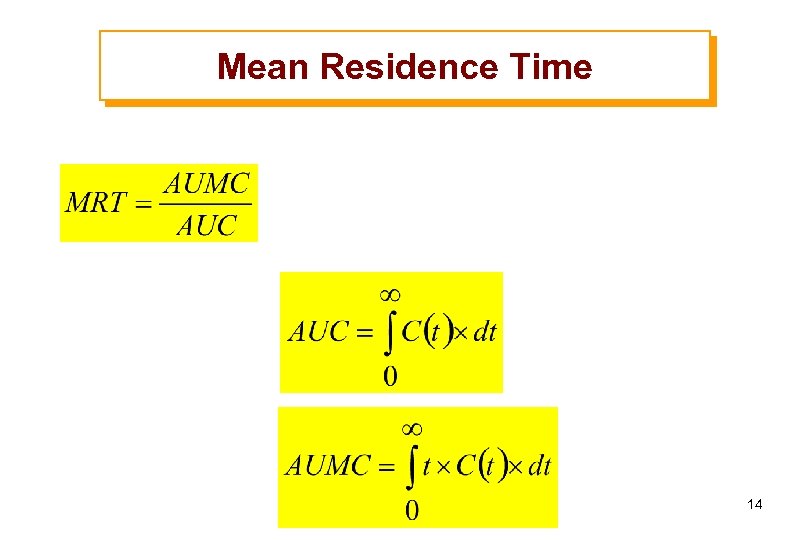Mean Residence Time 14 Mean Residence Time 14

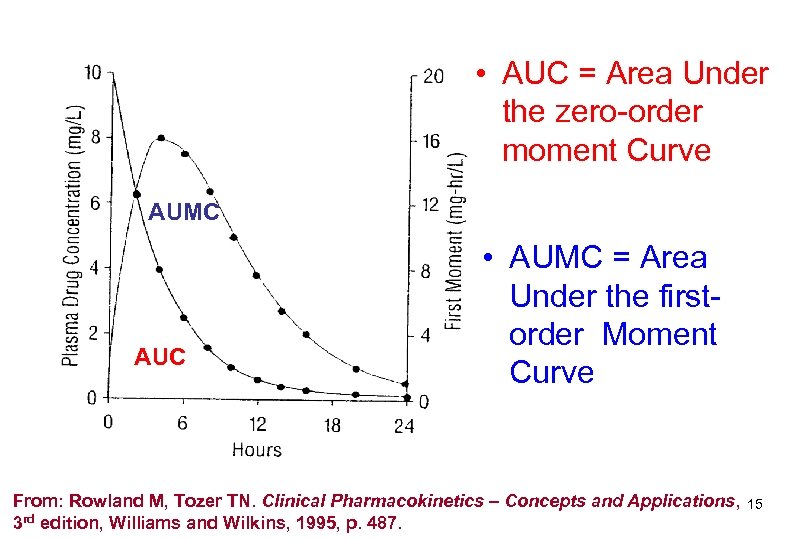• AUC = Area Under the zero-order moment Curve AUMC AUC • AUMC • AUC = Area Under the zero-order moment Curve AUMC AUC • AUMC = Area Under the firstorder Moment Curve From: Rowland M, Tozer TN. Clinical Pharmacokinetics – Concepts and Applications, 3 rd edition, Williams and Wilkins, 1995, p. 487. 15

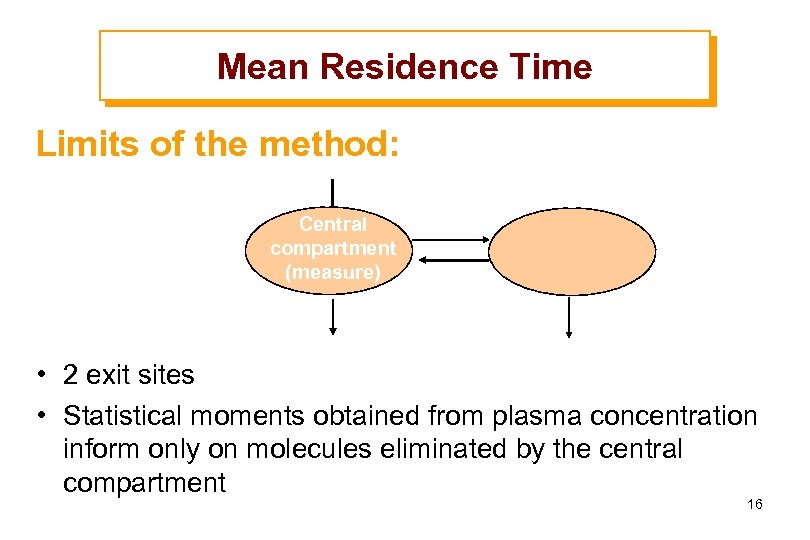Mean Residence Time Limits of the method: Central compartment (measure) • 2 exit sites Mean Residence Time Limits of the method: Central compartment (measure) • 2 exit sites • Statistical moments obtained from plasma concentration inform only on molecules eliminated by the central compartment 16

Computational methods • Non-compartmental analysis Area calculations Trapezes • Fitting with a poly-exponential equation Computational methods • Non-compartmental analysis Area calculations Trapezes • Fitting with a poly-exponential equation Equation parameters : Yi, li • Analysis with a compartmental model Model parameters : kij 17

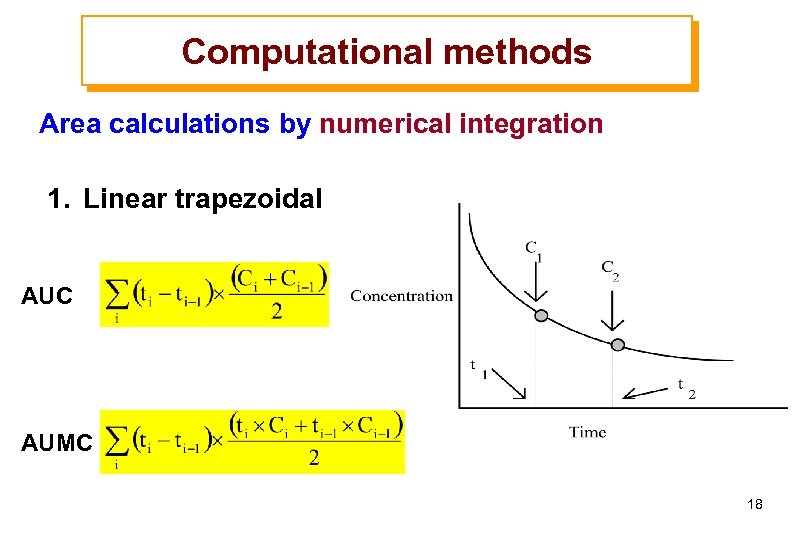Computational methods Area calculations by numerical integration 1. Linear trapezoidal AUC AUMC 18 Computational methods Area calculations by numerical integration 1. Linear trapezoidal AUC AUMC 18

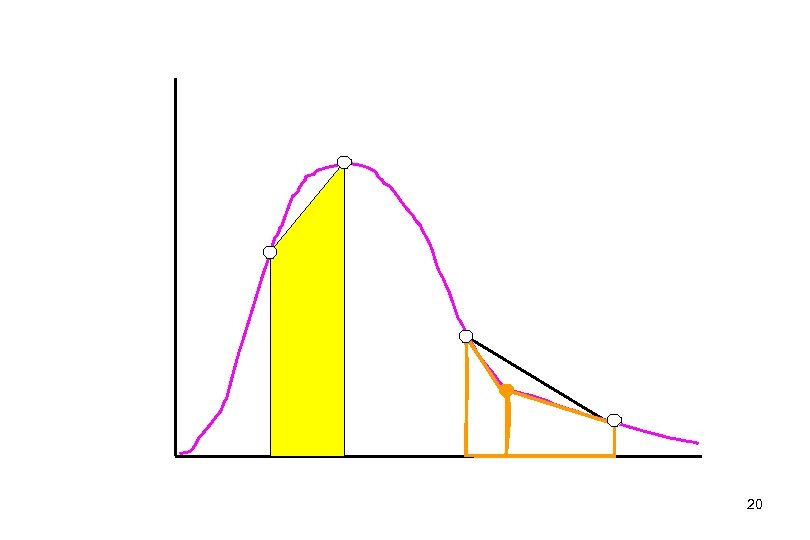
Computational methods Area calculations by numerical integration 1. Linear trapezoidal Advantages: Simple (can calculate Computational methods Area calculations by numerical integration 1. Linear trapezoidal Advantages: Simple (can calculate by hand) Disadvantages: • Assumes straight line between data points • If curve is steep, error may be large • Under or over estimation, depending on whether the curve is ascending of descending 19

20 20

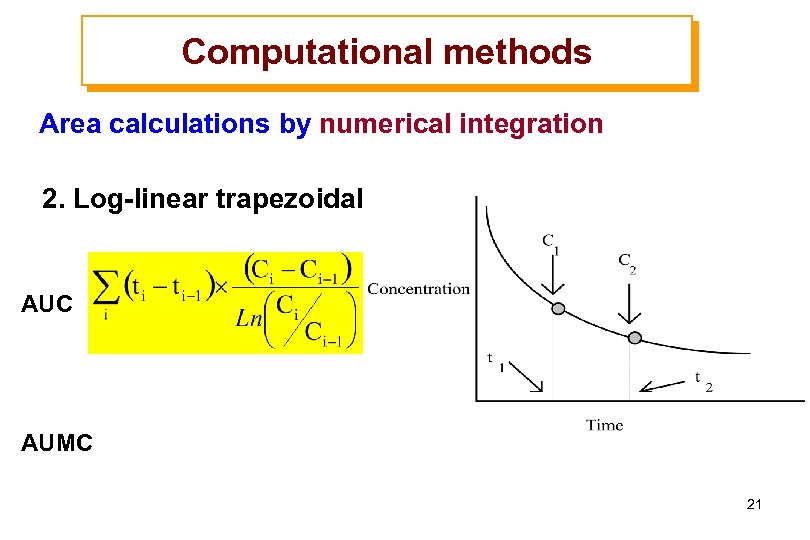Computational methods Area calculations by numerical integration 2. Log-linear trapezoidal AUC AUMC 21 Computational methods Area calculations by numerical integration 2. Log-linear trapezoidal AUC AUMC 21

Computational methods Area calculations by numerical integration 2. Log-linear trapezoidal < Linear trapezoidal Disadvantages: Computational methods Area calculations by numerical integration 2. Log-linear trapezoidal < Linear trapezoidal Disadvantages: Advantages: • Produces large errors on • Hand calculator an ascending curve, near • Very accurate for monothe peak, or steeply exponential declining polyexponential • Very accurate in late time points curve where interval between points is substantially increased 22

Computational methods Extrapolation to infinity Assumes loglinear decline 23 Computational methods Extrapolation to infinity Assumes loglinear decline 23

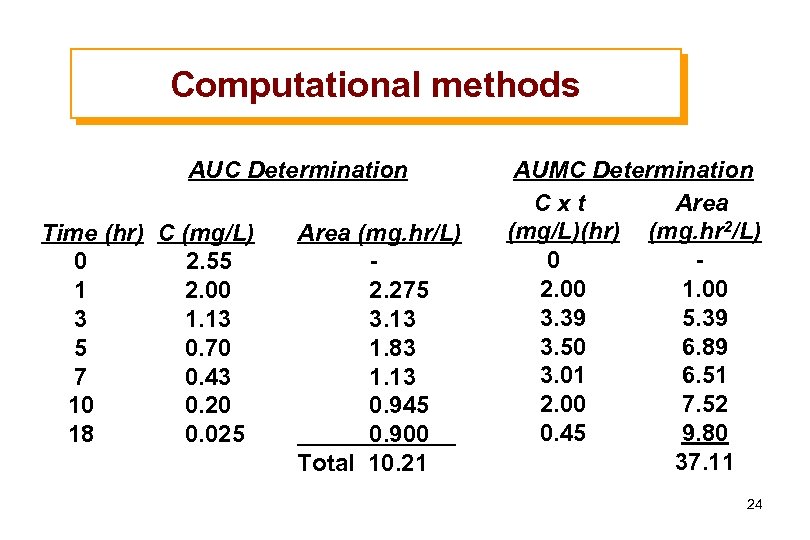Computational methods AUC Determination Time (hr) C (mg/L) 0 2. 55 1 2. 00 Computational methods AUC Determination Time (hr) C (mg/L) 0 2. 55 1 2. 00 3 1. 13 5 0. 70 7 0. 43 10 0. 20 18 0. 025 Area (mg. hr/L) 2. 275 3. 13 1. 83 1. 13 0. 945 0. 900 Total 10. 21 AUMC Determination Cxt Area (mg/L)(hr) (mg. hr 2/L) 0 2. 00 1. 00 3. 39 5. 39 3. 50 6. 89 3. 01 6. 51 2. 00 7. 52 0. 45 9. 80 37. 11 24

Non-compartmental analysis The Main PK parameters can be calculated using non-compartmental analysis • MRT Non-compartmental analysis The Main PK parameters can be calculated using non-compartmental analysis • MRT = AUMC / AUC • Clearance = Dose / AUC • Vss = Cl x MRT = Dose x AUMC AUC 2 • F% = AUC EV / AUC IV DEV = DIV 25

Computational methods • Non-compartmental analysis Area calculations Trapezes • Fitting with a poly-exponential equation Computational methods • Non-compartmental analysis Area calculations Trapezes • Fitting with a poly-exponential equation Equation parameters : Yi, li Area calculations • Analysis with a compartmental model Model parameters : kij 26

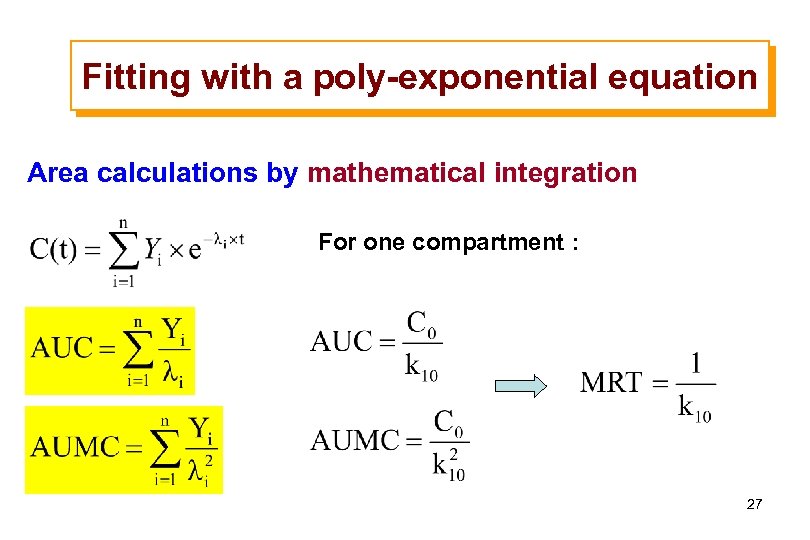Fitting with a poly-exponential equation Area calculations by mathematical integration For one compartment : Fitting with a poly-exponential equation Area calculations by mathematical integration For one compartment : 27

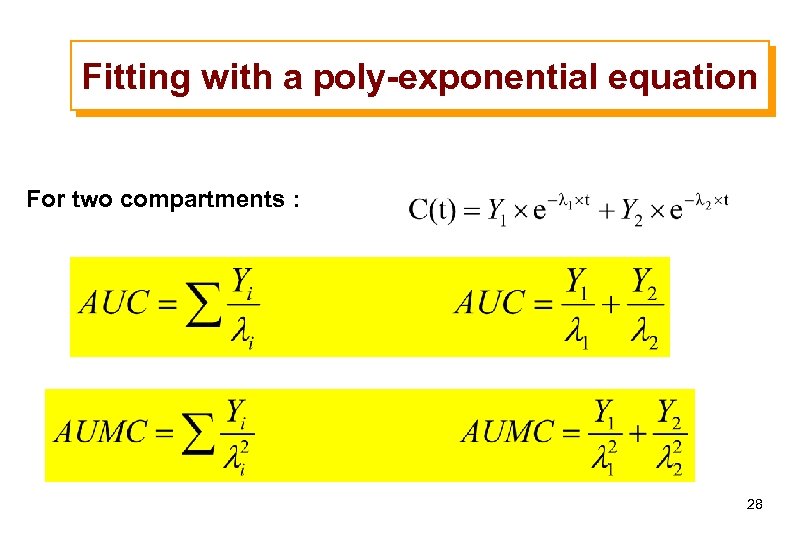Fitting with a poly-exponential equation For two compartments : 28 Fitting with a poly-exponential equation For two compartments : 28

Computational methods • Non-compartmental analysis Area calculations Trapezes • Fitting with a poly-exponential equation Computational methods • Non-compartmental analysis Area calculations Trapezes • Fitting with a poly-exponential equation Equation parameters : Yi, li • Analysis with a compartmental model Model parameters : kij Area calculations Direct MRT calculations 29

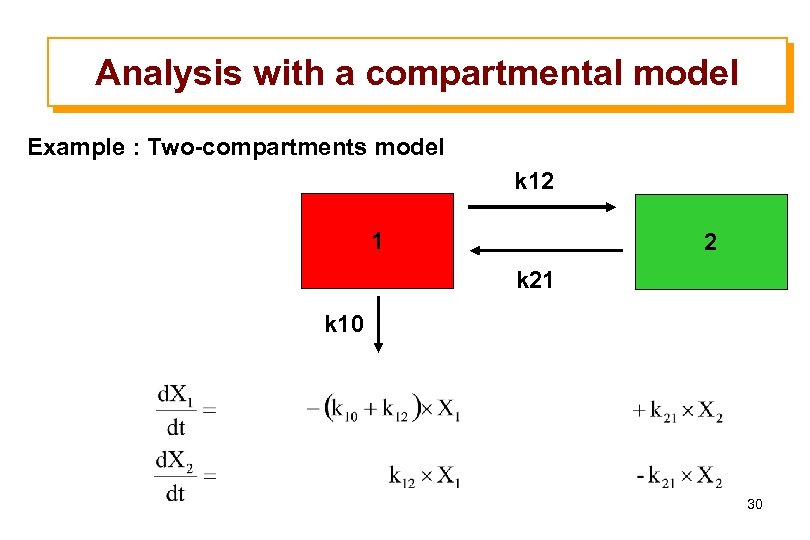Analysis with a compartmental model Example : Two-compartments model k 12 1 2 k Analysis with a compartmental model Example : Two-compartments model k 12 1 2 k 21 k 10 30

Analysis with a compartmental model Example : Two-compartments model K is the 2 x Analysis with a compartmental model Example : Two-compartments model K is the 2 x 2 matrix of the system of differential equations describing the drug transfer between compartments X 1 X 2 d. X 1/dt K= d. X 2/dt 31

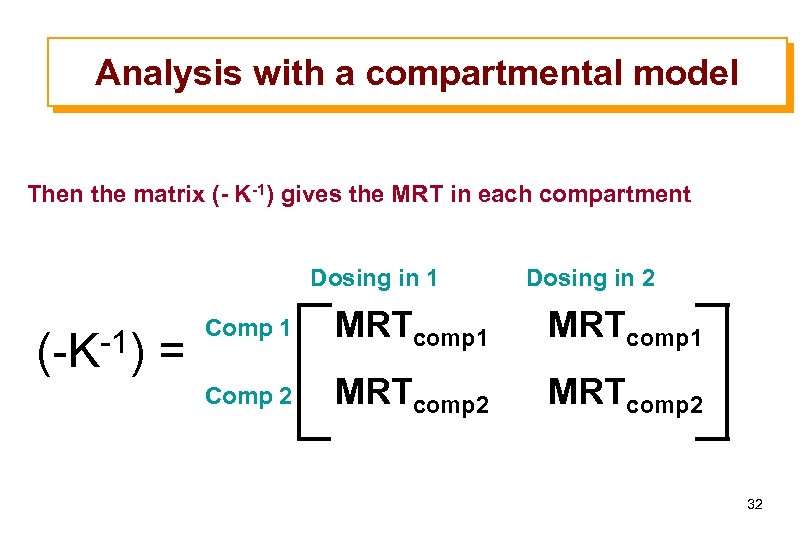Analysis with a compartmental model Then the matrix (- K-1) gives the MRT in Analysis with a compartmental model Then the matrix (- K-1) gives the MRT in each compartment Dosing in 1 (-K-1) = Dosing in 2 Comp 1 MRTcomp 1 Comp 2 MRTcomp 2 32

The Mean Residence Times Fundamental property of MRT : ADDITIVITY The mean residence time The Mean Residence Times Fundamental property of MRT : ADDITIVITY The mean residence time in the system is the sum of the mean residence times in the compartments of the system • Mean Absorption Time / Mean Dissolution Time • MRT in central and peripheral compartments 33

The Mean Absorption Time (MAT) 34 The Mean Absorption Time (MAT) 34

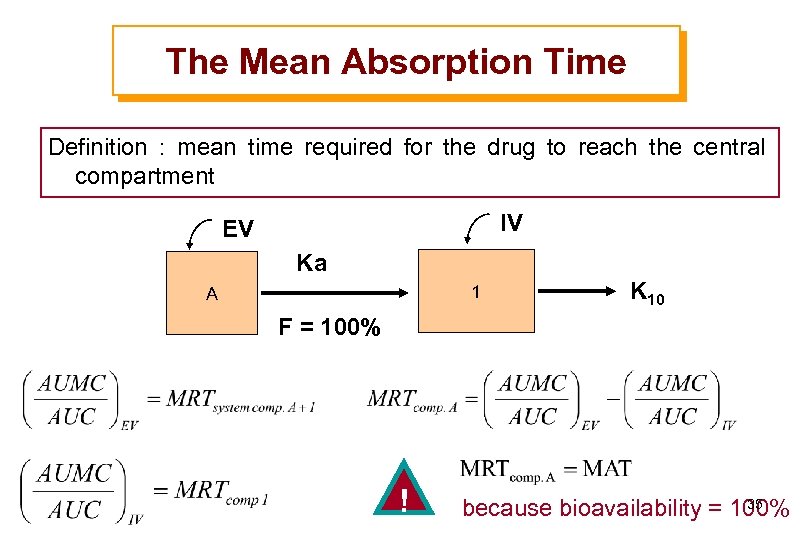The Mean Absorption Time Definition : mean time required for the drug to reach The Mean Absorption Time Definition : mean time required for the drug to reach the central compartment IV EV Ka 1 A K 10 F = 100% ! 35 because bioavailability = 100%

The Mean Absorption Time ! MAT and bioavailability • Actually, the MAT calculated from The Mean Absorption Time ! MAT and bioavailability • Actually, the MAT calculated from plasma data is the MRT at the injection site • This MAT does not provide information about the absorption process unless F = 100% • Otherwise the real MAT is : 36

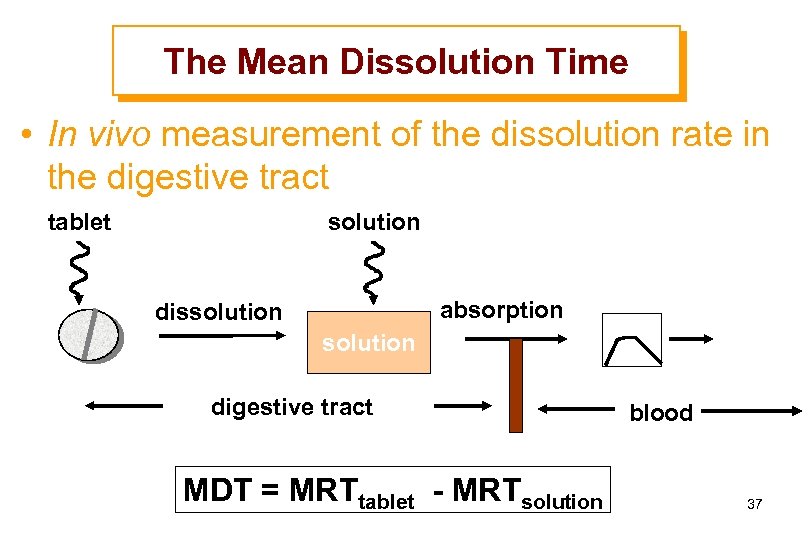The Mean Dissolution Time • In vivo measurement of the dissolution rate in the The Mean Dissolution Time • In vivo measurement of the dissolution rate in the digestive tract tablet solution absorption dissolution digestive tract MDT = MRTtablet - MRTsolution blood 37

Mean Residence Time in the Central Compartment (MRTC) and in the Peripheral (Tissues) Compartment Mean Residence Time in the Central Compartment (MRTC) and in the Peripheral (Tissues) Compartment (MRTT) 38

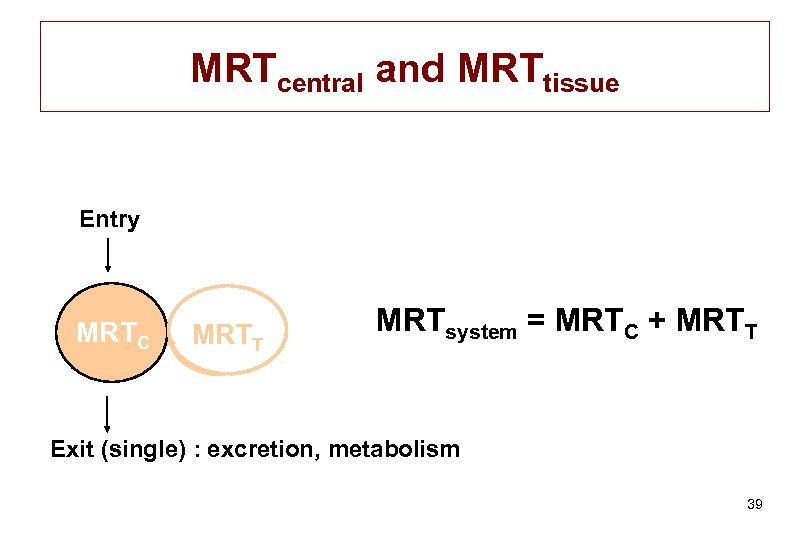MRTcentral and MRTtissue Entry MRTC MRTT MRTsystem = MRTC + MRTT Exit (single) : MRTcentral and MRTtissue Entry MRTC MRTT MRTsystem = MRTC + MRTT Exit (single) : excretion, metabolism 39

The Mean Transit Time (MTT) 40 The Mean Transit Time (MTT) 40

The Mean Transit Times (MTT) • Definition : – Average interval of time spent The Mean Transit Times (MTT) • Definition : – Average interval of time spent by a drug particle from its entry into the compartment to its next exit – Average duration of one visit in the compartment • Computation : – The MTT in the central compartment can be calculated for plasma concentrations after i. v. 41

The Mean Residence Number (MRN) 42 The Mean Residence Number (MRN) 42

The Mean Residence Number (MRN) • Definition : – Average number of times drug The Mean Residence Number (MRN) • Definition : – Average number of times drug particles enter into a compartment after their injection into the kinetic system – Average number of visits in the compartment – For each compartment : MRN = MRT MTT 43

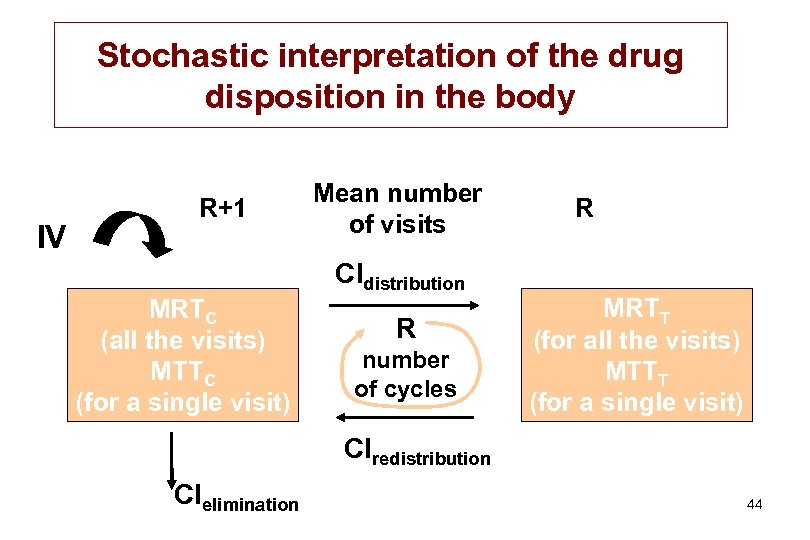Stochastic interpretation of the drug disposition in the body IV R+1 MRTC (all the Stochastic interpretation of the drug disposition in the body IV R+1 MRTC (all the visits) MTTC (for a single visit) Mean number of visits Cldistribution R number of cycles R MRTT (for all the visits) MTTT (for a single visit) Clredistribution Clelimination 44

Stochastic interpretation of the drug disposition in the body Computation : intravenous administration MRTsystem Stochastic interpretation of the drug disposition in the body Computation : intravenous administration MRTsystem = AUMC / AUC MRTC = AUC / C(0) MTTC = - C(0) / C’(0) MRTT = MRTsystem- MRTC R+1= MTTT = MRTC MTTC MRTT R 45

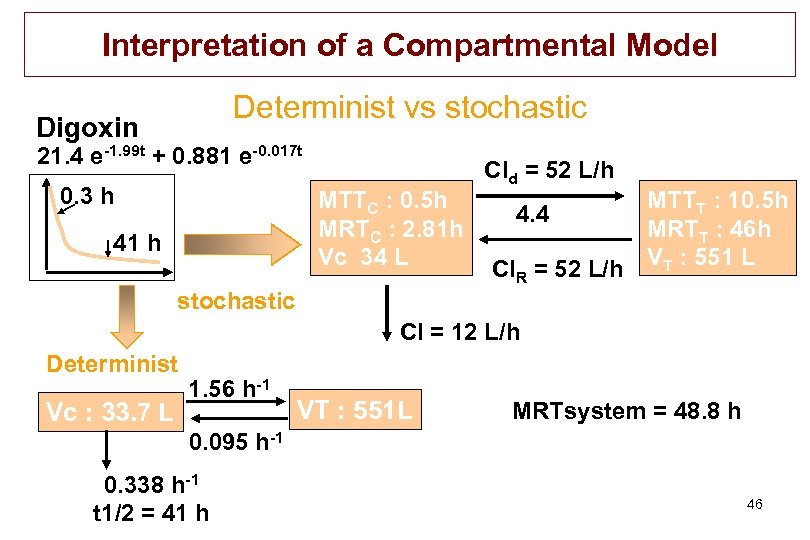Interpretation of a Compartmental Model Determinist vs stochastic Digoxin 21. 4 e-1. 99 t Interpretation of a Compartmental Model Determinist vs stochastic Digoxin 21. 4 e-1. 99 t + 0. 881 e-0. 017 t 0. 3 h MTTC : 0. 5 h MRTC : 2. 81 h Vc 34 L 41 h Cld = 52 L/h MTTT : 10. 5 h 4. 4 MRTT : 46 h Cl. R = 52 L/h VT : 551 L stochastic Cl = 12 L/h Determinist Vc : 33. 7 L 1. 56 h-1 VT : 551 L MRTsystem = 48. 8 h 0. 095 h-1 0. 338 h-1 t 1/2 = 41 h 46

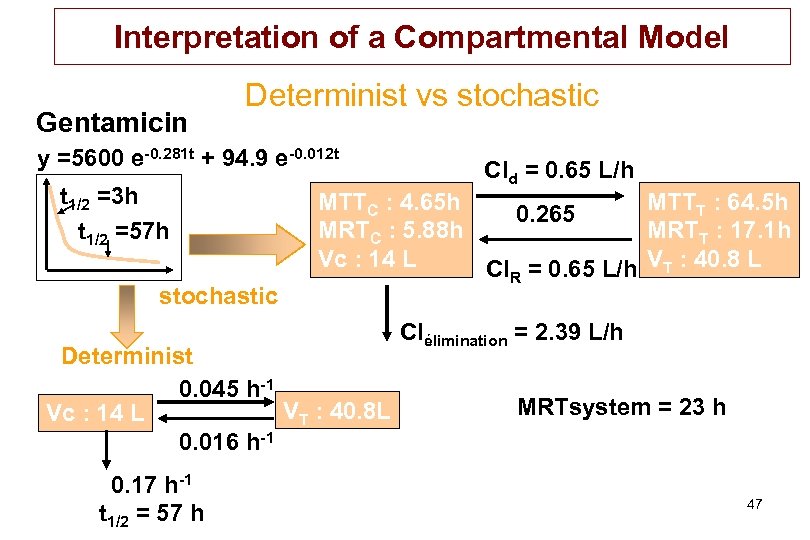Interpretation of a Compartmental Model Gentamicin Determinist vs stochastic y =5600 e-0. 281 t Interpretation of a Compartmental Model Gentamicin Determinist vs stochastic y =5600 e-0. 281 t + 94. 9 e-0. 012 t t 1/2 =3 h t 1/2 =57 h stochastic MTTC : 4. 65 h MTTT : 64. 5 h 0. 265 MRTC : 5. 88 h MRTT : 17. 1 h Vc : 14 L Cl. R = 0. 65 L/h VT : 40. 8 L Determinist 0. 045 h-1 VT : 40. 8 L Vc : 14 L 0. 016 h-1 0. 17 h-1 t 1/2 = 57 h Cld = 0. 65 L/h Clélimination = 2. 39 L/h MRTsystem = 23 h 47