Non-adiabatic electron transfer in chemistry and biology Igor

Non-adiabatic electron transfer in chemistry and biology Igor Kurnikov Dept. of Chemistry Carnegie Mellon Univ.

Electron Transfer reactions in biology. • Part of enzymatic oxidation-reduction reactions • Photosynthesis • Energy storage and transfer • Synthesis and chemical degradation • Protein folding control (SS bridge formation) • DNA repair • Enzyme activation

Unimolecular vs bimolecular ET reactions • Unimolecular ET reactions - same molecule or intermolecular complex. • Only “one” conformation although fluctuations of the structures can be important. • Bimolecular reactions - diffusion of reagents, many orientations and conformations. • A small fraction of configurations contributes to ET. • Bimolecular ET = Unimolecular ET + Docking

Marcus Theory: 1992 Nobel

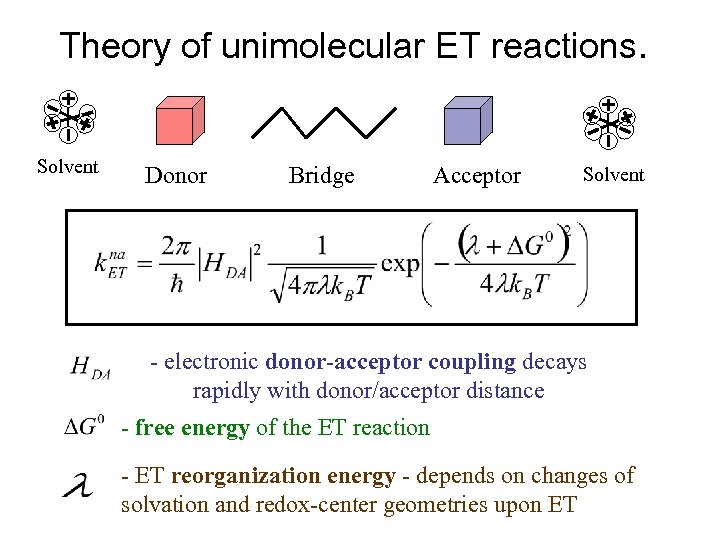
Theory of unimolecular ET reactions. Solvent Donor Bridge Acceptor Solvent - electronic donor-acceptor coupling decays rapidly with donor/acceptor distance - free energy of the ET reaction - ET reorganization energy - depends on changes of solvation and redox-center geometries upon ET

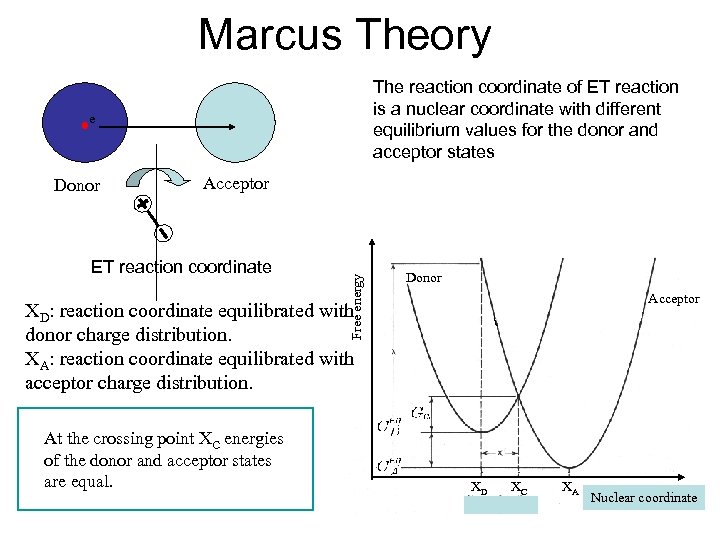
Marcus Theory The reaction coordinate of ET reaction is a nuclear coordinate with different equilibrium values for the donor and acceptor states e Acceptor ET reaction coordinate Free energy Donor Acceptor XD: reaction coordinate equilibrated with donor charge distribution. XA: reaction coordinate equilibrated with acceptor charge distribution. At the crossing point XC energies of the donor and acceptor states are equal. XD XC XA Nuclear coordinate

Calculation of the crossing point. Free energy of the donor state vs reaction coordinate: Free energy of the acceptor state: The crossing point can be calculated using these expressions: Activation energy can be expressed as: Where reorganization energy λ is:

Normal and Inverted Regimes of ET reactions G 0 Normal: increase of G 0 decreases the rate inverted normal No activation barrier maximum k. ET Inverted: decrease of G 0 decreases the rate In reality other factors also play a role in the electron transfer problem: distance between donor and acceptor, diffusion can be rate limiting step. The inverted regime has only been observed in rigid systems, such as proteins.

Quantum expression for ET rate. Slow(classical) coordinate y and Fast(quantum) coordinate q:

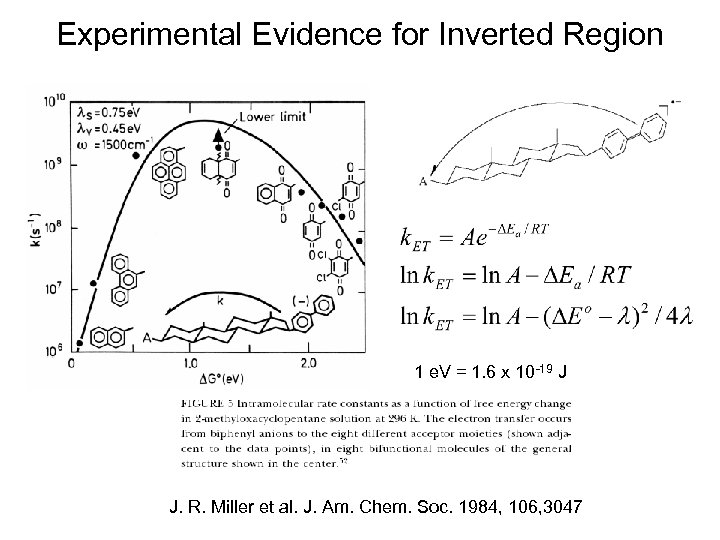
Experimental Evidence for Inverted Region 1 e. V = 1. 6 x 10 -19 J J. R. Miller et al. J. Am. Chem. Soc. 1984, 106, 3047

Finite-Difference Poisson-Boltzmann Equation calculations of electrostatic energies. Poisson-Bolzmann equation is solved on a rectangular grid by finite-difference method. Atomic charges are from AMBER force-field. PARSE atomic radii parameter set. Electrostatic energy calculated with:

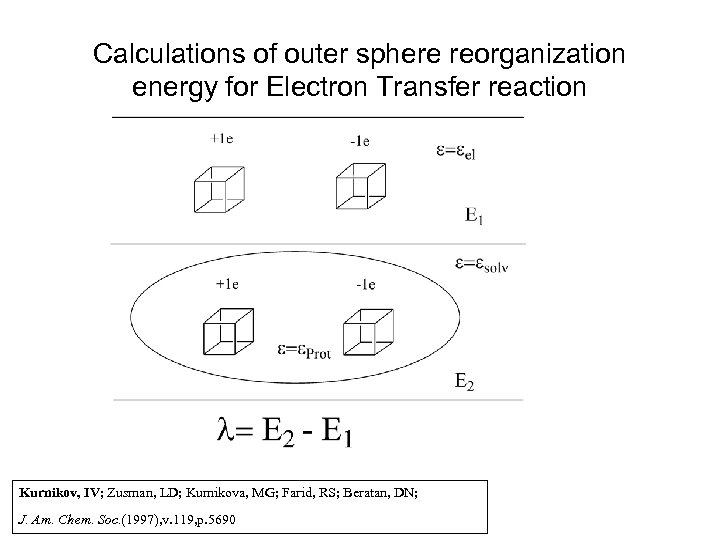
Calculations of outer sphere reorganization energy for Electron Transfer reaction Kurnikov, IV; Zusman, LD; Kurnikova, MG; Farid, RS; Beratan, DN; J. Am. Chem. Soc. (1997), v. 119, p. 5690

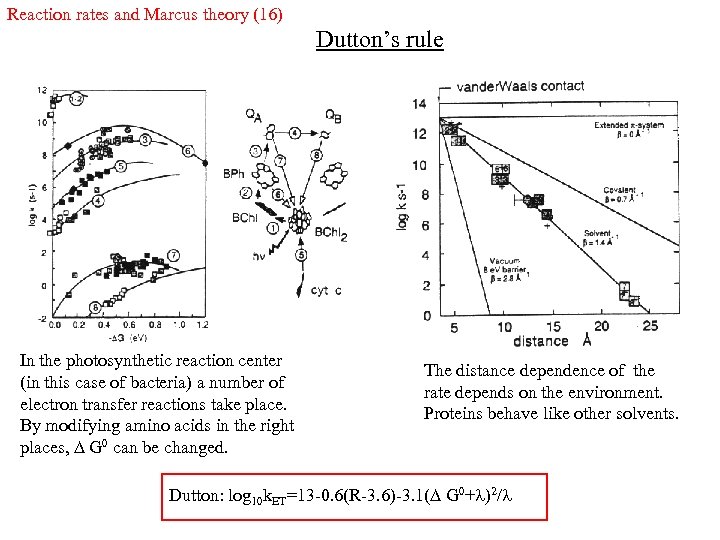
Reaction rates and Marcus theory (16) Dutton’s rule In the photosynthetic reaction center (in this case of bacteria) a number of electron transfer reactions take place. By modifying amino acids in the right places, G 0 can be changed. The distance dependence of the rate depends on the environment. Proteins behave like other solvents. Dutton: log 10 k. ET=13 -0. 6(R-3. 6)-3. 1( G 0+ )2/

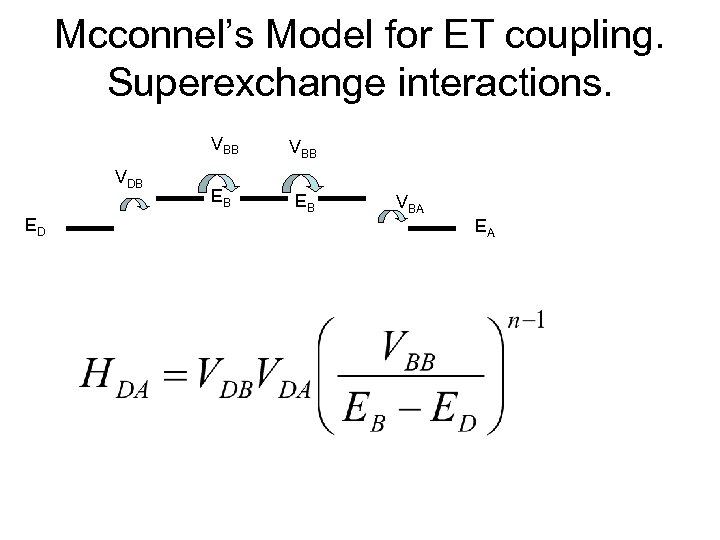
Mcconnel’s Model for ET coupling. Superexchange interactions. VBB VDB ED VBB EB EB VBA EA

PATHWAYS calculations of ET electronic coupling. prefactor = 0. 1 - 1. 0 e. V

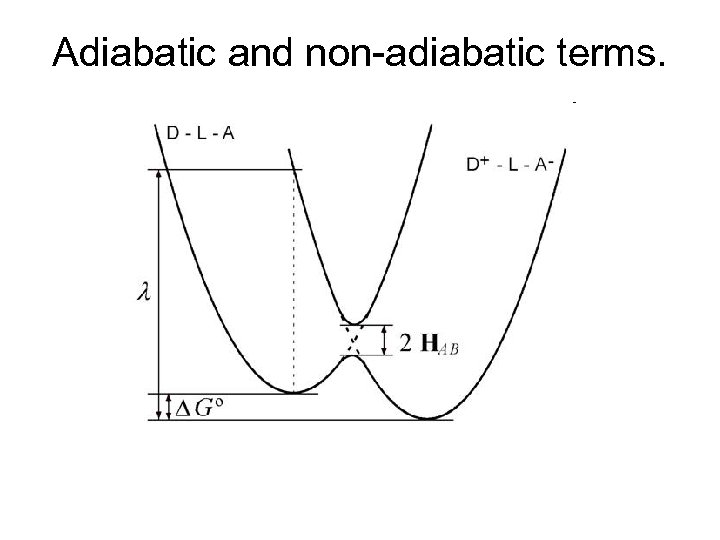
Adiabatic and non-adiabatic terms.

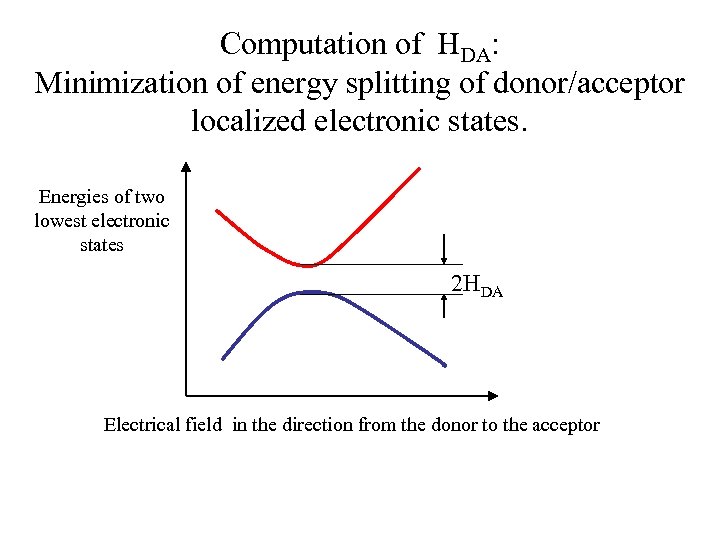
Computation of HDA: Minimization of energy splitting of donor/acceptor localized electronic states. Energies of two lowest electronic states 2 HDA Electrical field in the direction from the donor to the acceptor

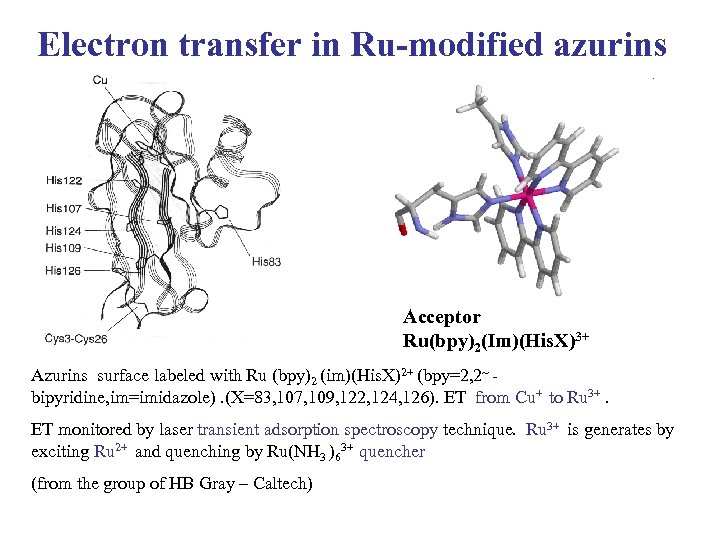
Electron transfer in Ru-modified azurins Acceptor Ru(bpy)2(Im)(His. X)3+ Azurins surface labeled with Ru (bpy)2 (im)(His. X)2+ (bpy=2, 2~ bipyridine, im=imidazole). (X=83, 107, 109, 122, 124, 126). ET from Cu+ to Ru 3+. ET monitored by laser transient adsorption spectroscopy technique. Ru 3+ is generates by exciting Ru 2+ and quenching by Ru(NH 3 )63+ quencher (from the group of HB Gray – Caltech)

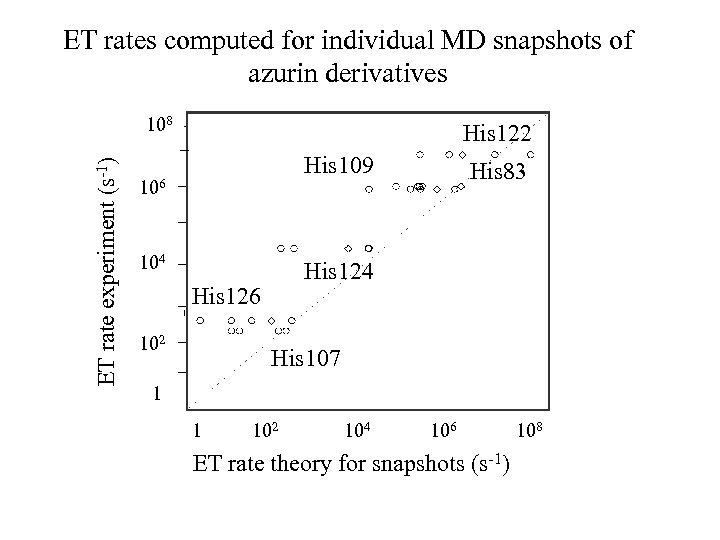
ET rates computed for individual MD snapshots of azurin derivatives ET rate experiment (s-1) 108 His 122 His 109 106 104 His 126 102 His 83 His 107 1 1 102 104 106 ET rate theory for snapshots (s-1) 108

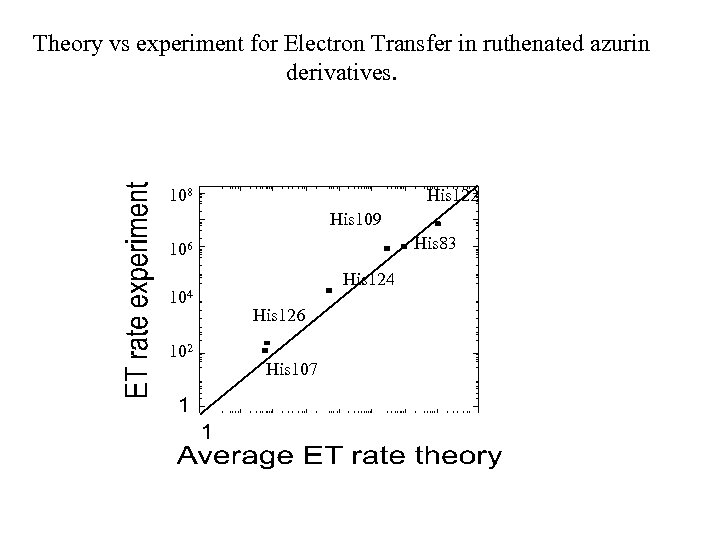
(s-1) Theory vs experiment for Electron Transfer in ruthenated azurin derivatives. 108 His 122 His 109 His 83 106 104 102 His 124 His 126 104 His 107 106 108 (s-1)

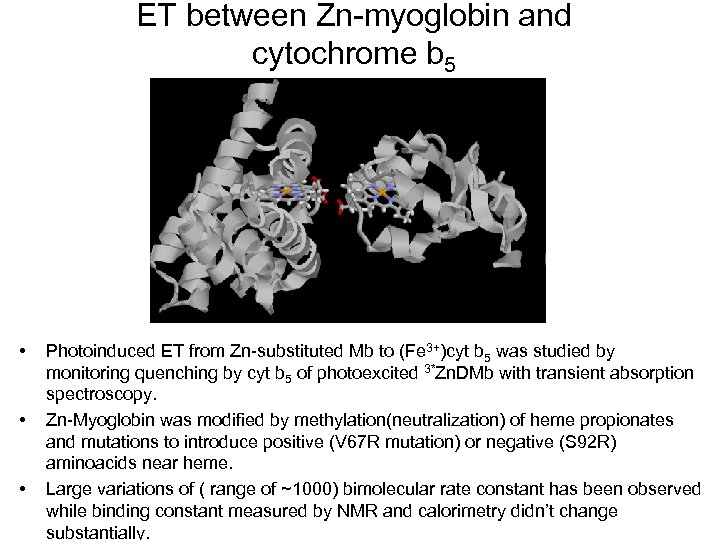
ET between Zn-myoglobin and cytochrome b 5 • • • Photoinduced ET from Zn-substituted Mb to (Fe 3+)cyt b 5 was studied by monitoring quenching by cyt b 5 of photoexcited 3*Zn. DMb with transient absorption spectroscopy. Zn-Myoglobin was modified by methylation(neutralization) of heme propionates and mutations to introduce positive (V 67 R mutation) or negative (S 92 R) aminoacids near heme. Large variations of ( range of ~1000) bimolecular rate constant has been observed while binding constant measured by NMR and calorimetry didn’t change substantially.

Diffusion and rapid-equilibration limits of bimolecular ET reactions • Diffusion limit: ET in “active” configuration reactions are faster than equilibration. • One needs to consider explicitly diffusion from initially prepared configurations to the “active” configurations. ET rates in “active” configurations are not important as long as they are large enough. • Rapid-equilibration limit: the system is equilibrated over configurations. Only free energies of different configurations and unimolecular rates in these configurations are important. Diffusive dynamics is not important. This regime is realized for weakly bound protein-protein complexes and slow ET rates in the complex.

Rate of bimolecular ET in rapidequilibration regime. - unimolecular ET rate in the i-th configuration strongly geometry dependent. The system consist of two proteins in volume V - Second-order bimolecular ET rate constant

Effective energy approach to calculate relative bimolecular ET rates. Effective energy combines intermolecular energy and ET rate for a configuration i: Ratio of bimolecular ET rates for different experimental conditions (chemically modified proteins, different p. H etc. ): Second bracket is close to 1 if zero energy correspond to isolated proteins and bimolecular ET is described by second order rate constant k(2).

Computation of effective “ET free energy” changes. Effective free energy changes can be calculated using free energy perturbation method and Monte Carlo simulations with the effective energy functional: Only a small number of configurations will be sampled as donor-acceptor coupling rapidly decays with distance and the effective energy increases.

Calculations of effective energies of protein configurations (intermolecular interaction energies and ET rates). - Computed using PATHWAYS model: Ei – interaction energies computed using continuum electrostatics FDPB approach ( charges in the field model – one protein in the field of another or more expensive – 3 FDPB calculations in each point of MC trajectory – take care of desolvation). Vd. W contribution computed with excluded volume approach (fast) or with Lennard-Jones atom-atom interaction potentials.

Electronic coupling of surface atoms of myoglobin (left) and cytochrome- b 5 (right) to their hemes. Red - strong electronic coupling to the heme Blue - weak electronic coupling to the heme

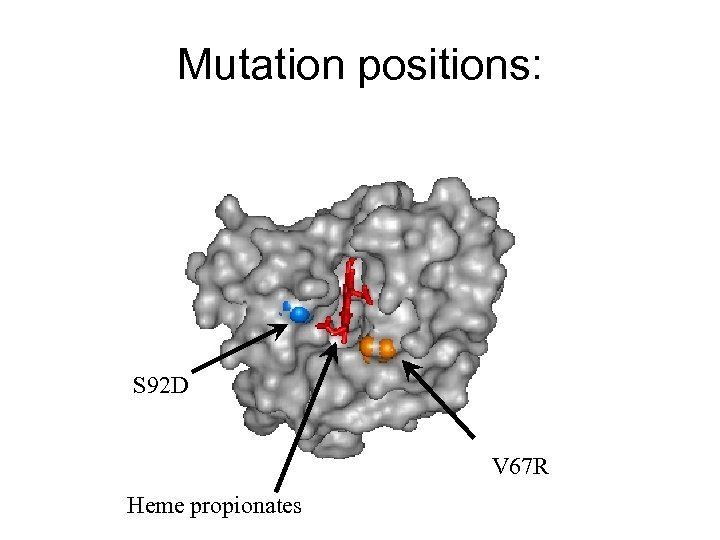
Mutation positions: S 92 D V 67 R Heme propionates

MC trajectory of Zn-myoglobin and cytochrome b 5 with effective “ET” energy.

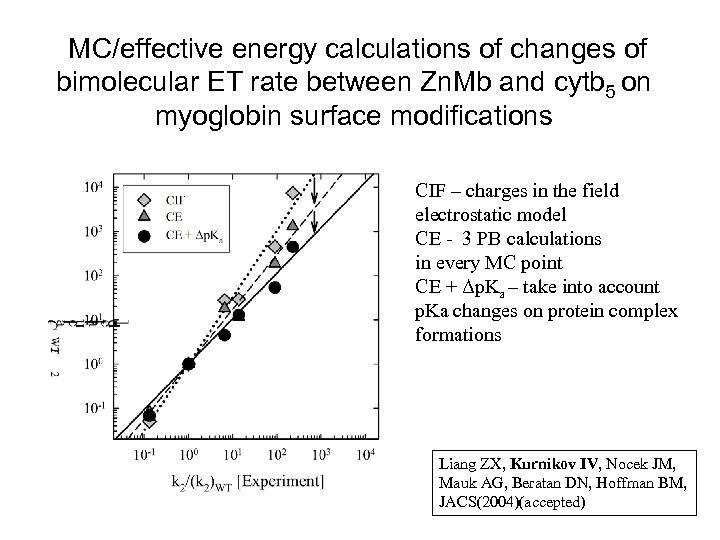
MC/effective energy calculations of changes of bimolecular ET rate between Zn. Mb and cytb 5 on myoglobin surface modifications CIF – charges in the field electrostatic model CE - 3 PB calculations in every MC point CE + Δp. Ka – take into account p. Ka changes on protein complex formations Liang ZX, Kurnikov IV, Nocek JM, Mauk AG, Beratan DN, Hoffman BM, JACS(2004)(accepted)

Bimolecular ET. Conclusions. • New Monte-Carlo/effective energy approach for quantitative studies of bimolecular ET reactions in fast-equilibration regime has been introduced and applied to study ET reaction between Zn-myoglobin and cytochrome b 5 • ET rate between Zn-Mb and cyt b 5 is controlled by the stability of the interprotein configurations with strong donor/acceptor coupling. Configurations with strongest binding energy do not contribute to ET. • Protonation p. Ka changes upon Zn-myoglobin modifications and on protein binding are important. • Torsional flexibility is needed? Fast-equilibration limit is not valid for most positively charged derivative? Are p. Ks needed to be recomputed dynamically?

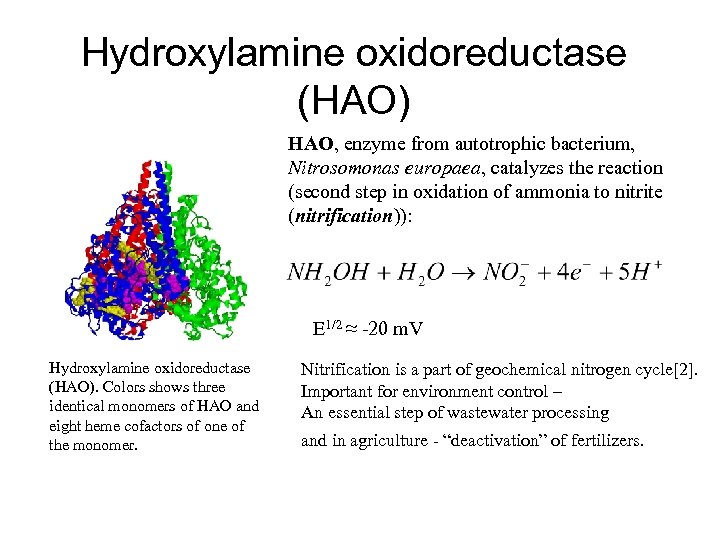
Hydroxylamine oxidoreductase (HAO) HAO, enzyme from autotrophic bacterium, Nitrosomonas europaea, catalyzes the reaction (second step in oxidation of ammonia to nitrite (nitrification)): E 1/2 ≈ -20 m. V Hydroxylamine oxidoreductase (HAO). Colors shows three identical monomers of HAO and eight heme cofactors of one of the monomer. Nitrification is a part of geochemical nitrogen cycle[2]. Important for environment control – An essential step of wastewater processing and in agriculture - “deactivation” of fertilizers.

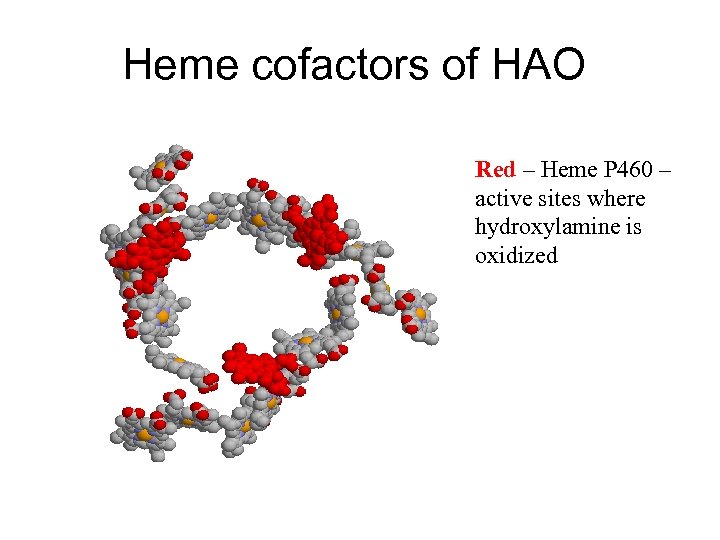
Heme cofactors of HAO Red – Heme P 460 – active sites where hydroxylamine is oxidized

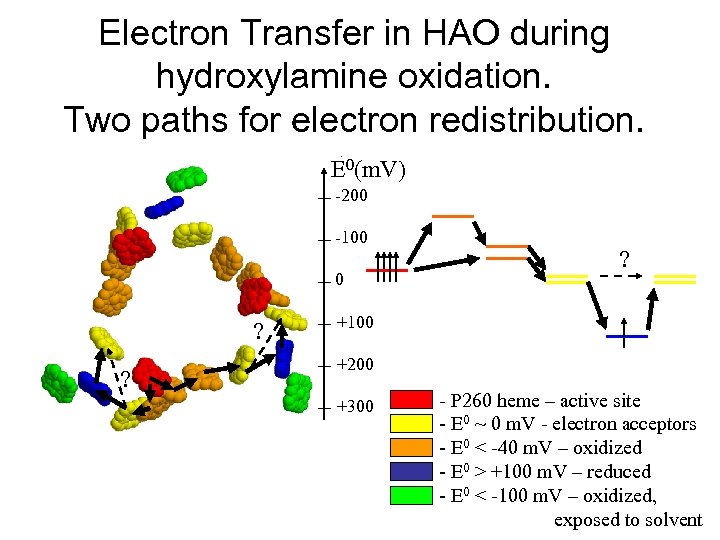
Electron Transfer in HAO during hydroxylamine oxidation. Two paths for electron redistribution. E 0(m. V) -200 -100 0 ? ? ? +100 +200 +300 - P 260 heme – active site - E 0 ~ 0 m. V - electron acceptors - E 0 < -40 m. V – oxidized - E 0 > +100 m. V – reduced - E 0 < -100 m. V – oxidized, exposed to solvent

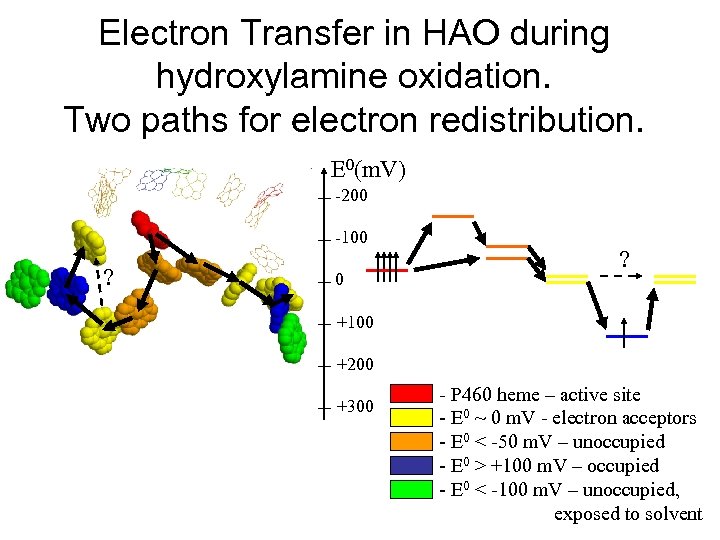
Electron Transfer in HAO during hydroxylamine oxidation. Two paths for electron redistribution. E 0(m. V) -200 -100 ? +100 +200 +300 - P 460 heme – active site - E 0 ~ 0 m. V - electron acceptors - E 0 < -50 m. V – unoccupied - E 0 > +100 m. V – occupied - E 0 < -100 m. V – unoccupied, exposed to solvent

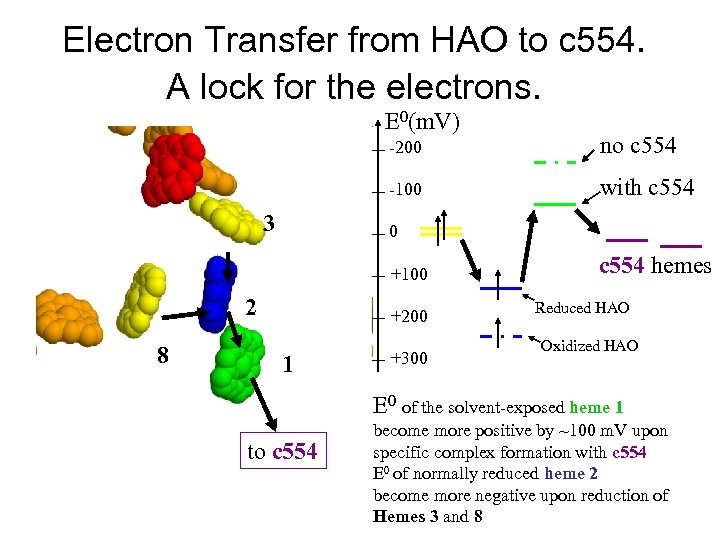
Electron Transfer from HAO to c 554. A lock for the electrons. E 0(m. V) -200 -100 3 no c 554 with c 554 0 +100 2 8 +200 1 +300 c 554 hemes Reduced HAO Oxidized HAO E 0 of the solvent-exposed heme 1 to c 554 become more positive by ~100 m. V upon specific complex formation with c 554 E 0 of normally reduced heme 2 become more negative upon reduction of Hemes 3 and 8

Biological nitrogen fixation reaction. Even without Mg. ATP ammonia synthesis is favored at 298 K and p. H 7, with an estimated G 0=-15. 2 kcal/mol. Substrate reduction by nitrogenase involves three basic types of electron-transfer reactions: • the reduction of Fe protein by electron carriers such as ferredoxin and flavodoxin in vivo or dithionite in vitro • transfer of single electrons from Fe protein to Mo. Fe protein in a Mg. ATP-dependent process with a minimal stoichiometry of two Mg. ATP hydrolyzed per electron transfered • electron transfer to the substrate at the active site within the Mo. Fe protein.

Motivation. • In the nitrogenase cycle the role for ATP hydrolysis is to control the electron-transfer “gate” between protein components. How this is accomplished is the one of the two main unanswered questions about the nitrogenase mechanism (the other being how substrates are reduced at the cofactor).

Nitrogenase complex. Av 1 Fe. Moco cofactor P Cluster [Fe 4 S 4]S 4 Cys Av 2 20 Å 2 x Mg. ATP

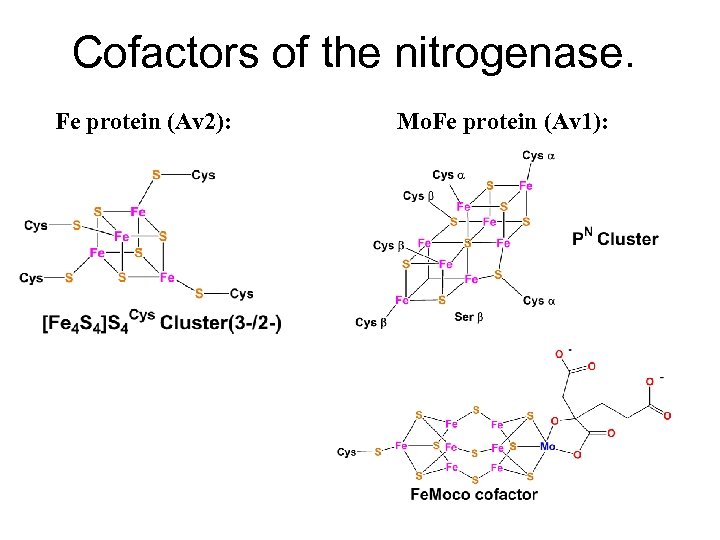
Cofactors of the nitrogenase. Fe protein (Av 2): Mo. Fe protein (Av 1):

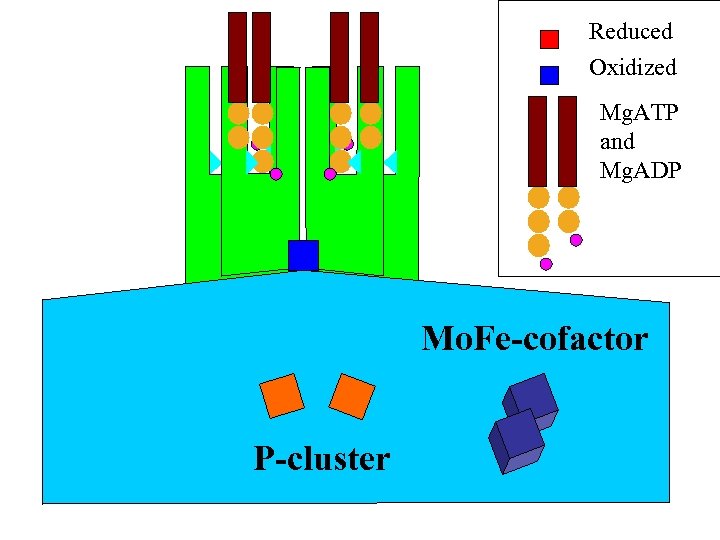
Reduced Oxidized Mg. ATP and Mg. ADP Mo. Fe-cofactor P-cluster

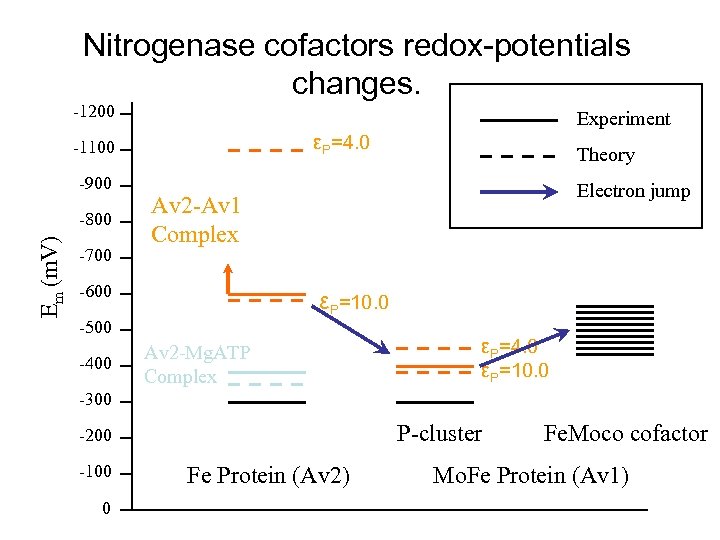
Nitrogenase cofactors redox-potentials changes. -1200 Experiment εP=4. 0 -1100 -900 Em (m. V) -800 -700 Electron jump Av 2 -Av 1 Complex -600 εP=10. 0 -500 -400 Theory Av 2 -Mg. ATP Complex εP=4. 0 εP=10. 0 -300 P-cluster -200 -100 0 Fe Protein (Av 2) Fe. Moco cofactor Mo. Fe Protein (Av 1)

Computation of ET rates in nitrogenase. ET Step Don/Acc coupling HDA(e. V) Reorg energy λ(e. V) ET free energy ΔG 0(e. V) ET rate k. ET(s-1) [Fe 4 S 4]S 4 > Pcluster 3. *10 -6 0. 3 - 0. 5 -0. 4 - -0. 2 4. *104 2. *105 P-cluster > Fe. Moco 1. *10 -5 0. 2 - 0. 4 +0. 1 +0. 2 5. 0*103 – 5. 0*104 [Fe 4 S 4]S 4 > Pcluster (concerted ) 101 – 103

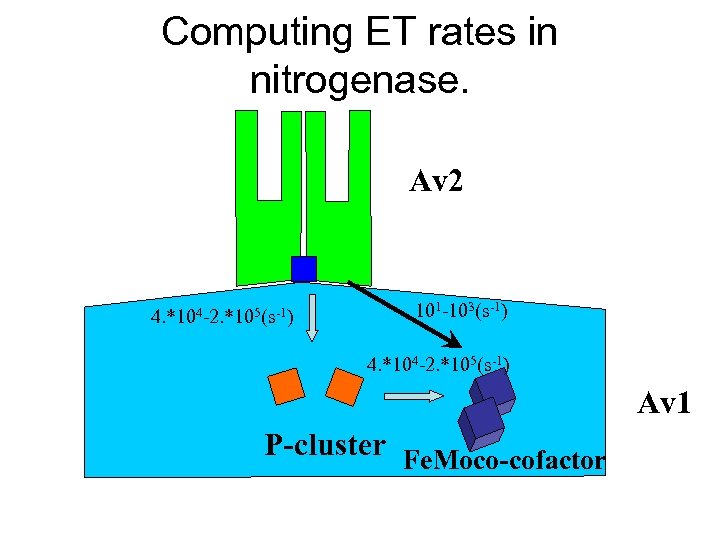
Computing ET rates in nitrogenase. Av 2 4. *104 -2. *105(s-1) 101 -103(s-1) 4. *104 -2. *105(s-1) Av 1 P-cluster Fe. Moco-cofactor