NMR Spectroscopy Gunther Chapters 1 4 Basic

NMR Spectroscopy, Gunther: Chapters 1 & 4 Basic One and Two Dimensional NMR Spectroscopy, Friebolin; Chapter 2 Nuclear Magnetic Resonance Spectroscopy, Lambert and Mazzola Chapter 3

Tuning Training Tues. 2/6 10 AM Wed 2/7 10 AM Thurs. 2/10 12: 30

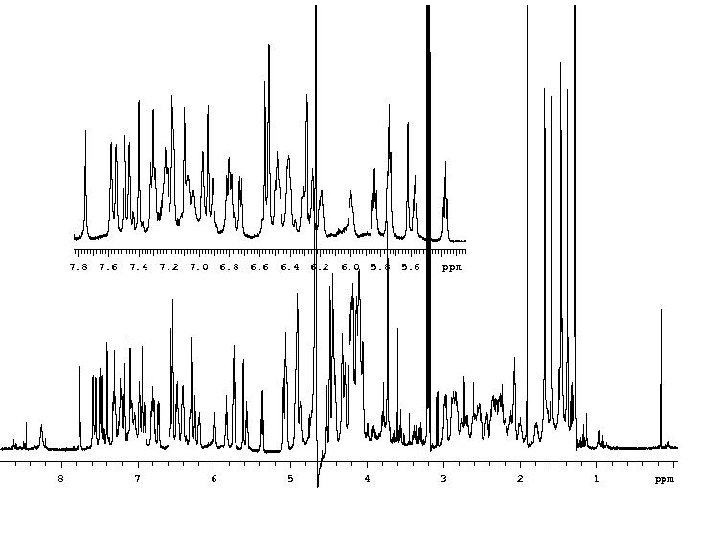
Chemical Shift A molecule is placed in a magnetic field, nuclei precess at a rate corresponding to the resonant frequency for that nucleus at that magnetic field. But, all nuclei do not see the exact same field. . . the resonance frequency of a particular nucleus in a molecule is affected by molecular structure. electrons within the molecule shield the nuclei. The field at the nucleus does not equal the applied field. Thus, the distribution of electrons affect the resonance frequency of the nucleus. The nuclear shielding is proportional to the magnetic field, a 60 Hz shielding at 14. 1 Tesla (600 Mhz) will be a 90 Hz shielding at 21. 1 Tesla (900 MHz) The standard units for chemical shift are parts per million (ppm). = [(Breference - Bsample)/Breference] * 106 ppm Chemical shift is a molecular parameter, independent of the size of the magnet, dependent upon only sample conditions such as solvent and temperature.

Reference Compounds For chemical shift to be a parameter comparable between experiments, a standard for each nucleus must be chosen and assigned a chemical shift value (normally 0). For proton: the standard is normally tetramethylsilane, Si(CH 3)4, (TMS). An alternative, especially for solutions in water is sodium 3 -trimethylsilylproprionate 2, 2, 3, 3, d 4, Me 3 Si. CD 2 CO 2 Na, (TSP). 2, 2 -dimethyl-silapentane-5 -sulfonic acid (DSS) For Carbon: TMS (or TSP, DSS) = 0 ppm For Nitrogen: liquid ammnonia = 0 ppm Fluorine: CFCl 3 = 0 Phosphorus: Phosphoric acid = 0 External Reference Compounds/Internal Reference Compounds

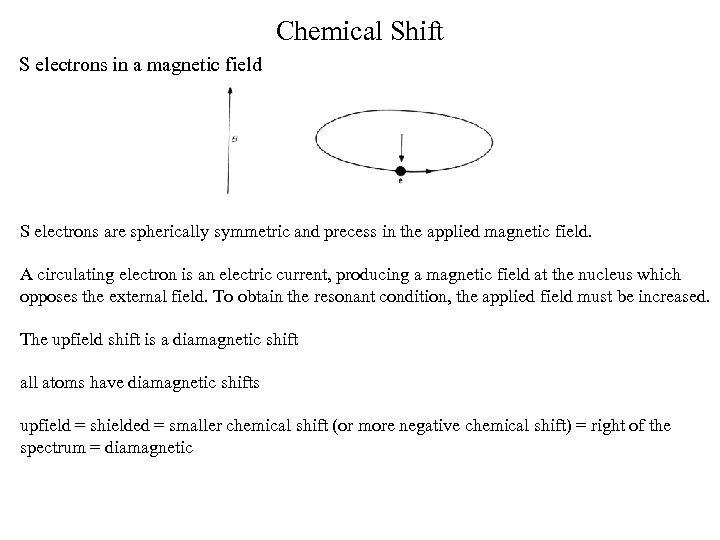
Chemical Shift S electrons in a magnetic field S electrons are spherically symmetric and precess in the applied magnetic field. A circulating electron is an electric current, producing a magnetic field at the nucleus which opposes the external field. To obtain the resonant condition, the applied field must be increased. The upfield shift is a diamagnetic shift all atoms have diamagnetic shifts upfield = shielded = smaller chemical shift (or more negative chemical shift) = right of the spectrum = diamagnetic

Chemical Shift Electrons in p-orbitals are not spherical and produce large magnetic fields at the nucleus. These are paramagnetic shifts downfield = deshielded = larger positive chemical shift = left of the spectrum = paramagnetic Hydrogen has no p-orbitals, thus no paramagnetic shifts from their own electrons. This is the primary reason proton chemical shifts vary over ~15 ppm range whereas other nuclei vary over 100's to 1000's of ppm. The other result of no paramagnetic shifts is that the diamagnetic term has more direct influence. When both terms are present, it can be more difficult to discern the individual contributions of each.

s = s(local dia) + s(local para) + s. N + s. R + se + si s. N = magnetic anisotropy of neigboring groups s. R = ring current effect se = electric field effect si = intermolecular interactions

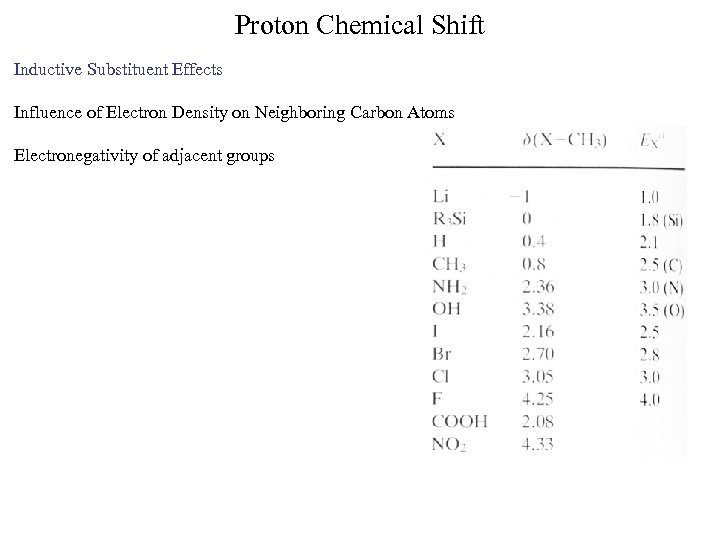
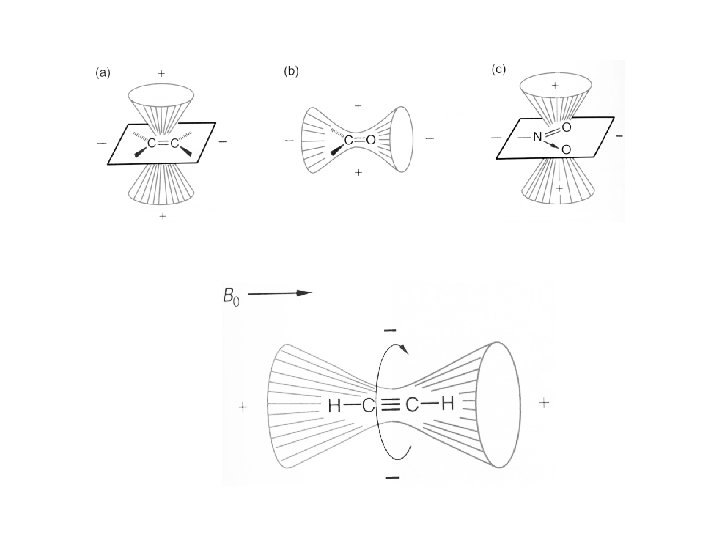
Proton Chemical Shift Inductive Substituent Effects Influence of Electron Density on Neighboring Carbon Atoms Electronegativity of adjacent groups

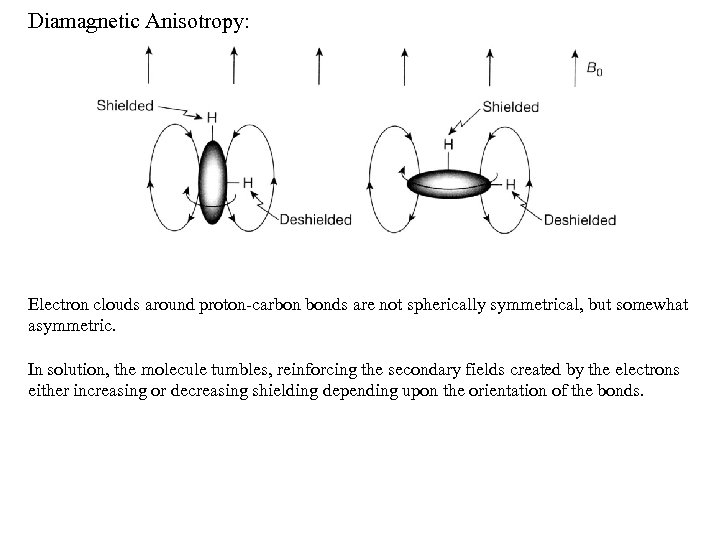
Diamagnetic Anisotropy: Electron clouds around proton-carbon bonds are not spherically symmetrical, but somewhat asymmetric. In solution, the molecule tumbles, reinforcing the secondary fields created by the electrons either increasing or decreasing shielding depending upon the orientation of the bonds.

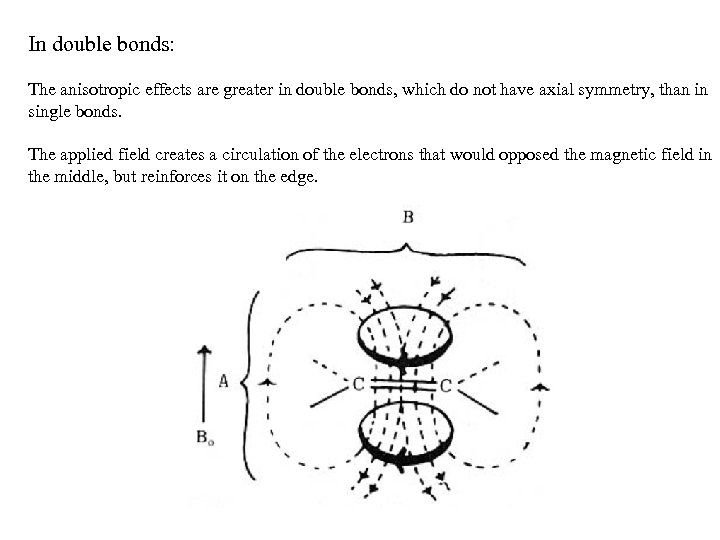
In double bonds: The anisotropic effects are greater in double bonds, which do not have axial symmetry, than in single bonds. The applied field creates a circulation of the electrons that would opposed the magnetic field in the middle, but reinforces it on the edge.

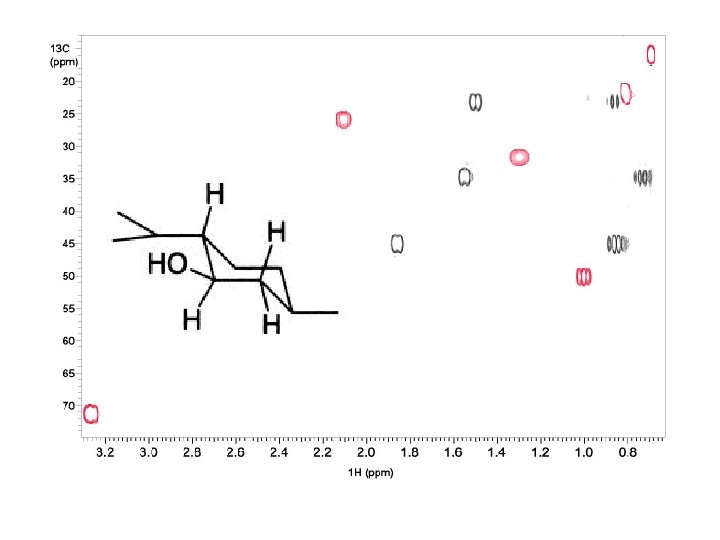
Ring Current Effect: When a molecule of benzene is oriented perpendicular to the magnetic field, the -electrons precess the same way. An approximate formula for the ring current shift is: (ppm) = (1 - 3 cos 2 )/r 3 Ring Current shifts affect nuclei other than proton, but the amount of shift is the same.

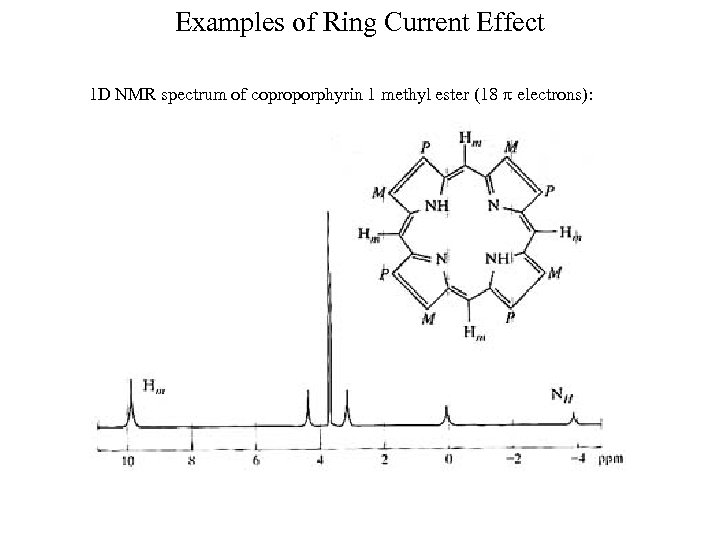
Examples of Ring Current Effect 1 D NMR spectrum of coproporphyrin 1 methyl ester (18 electrons):

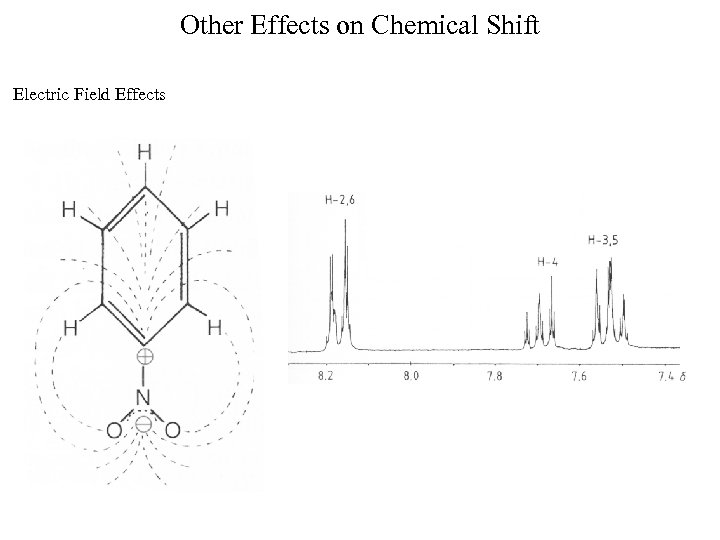
Other Effects on Chemical Shift Electric Field Effects

Other Effects on Chemical Shift Solvent Effects/intermolecular effects: Dissolved substances affected: 1) Polarity of solvent 2) Magnetic Anisotropy of solvent (especially C 6 D 6) When resonances are not resolved in one solvent, switch solvents- possibly improve dispersion

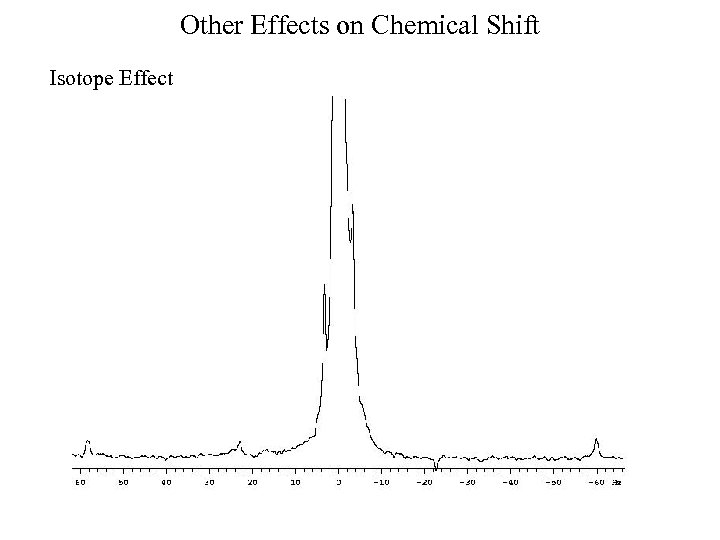
Other Effects on Chemical Shift Isotope Effect

Other Effects on Chemical Shift Metals, Paramagnetic Contact shifts and Pseudocontact shifts: Protons bound to metals will experience large shifts due to the asymmetry in the valence oribtals. Unpaired electrons, from paramagnetic species, can lead to contact or pseudocontact shifts.

Water Exchangeable Proton Chemical Shifts Concentration, Temperature and Hydrogen Bonding: OH, NH 2, CO 2 H The chemical shift of these are all VERY dependent upon temperature, solvent, concentration. H 2 O chemical shift changes at a rate of ~0. 01 ppm/ºC; thus, H 2 O chemical shift is ~4. 77 ppm at 25º, but 4. 67 ppm at 35º or 4. 87 ppm at 15º. Also, linewidth for these protons can be very large due to solvent exchange Intramolecular and intermolecular Hydrogen bonds affect chemical shift. The strength (or presence) of intermolecular Hydrogen bonds is concentration, temperature and solvent dependent. Intramolecular Hydrogen bonds can be temperature and solvent dependent as well, but should not be concentration dependent. Protons in Hydrogen bonds are shifted downfield.

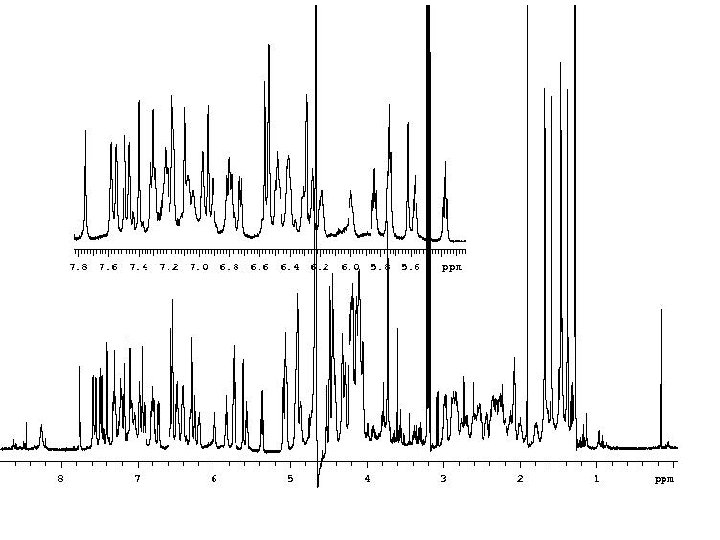
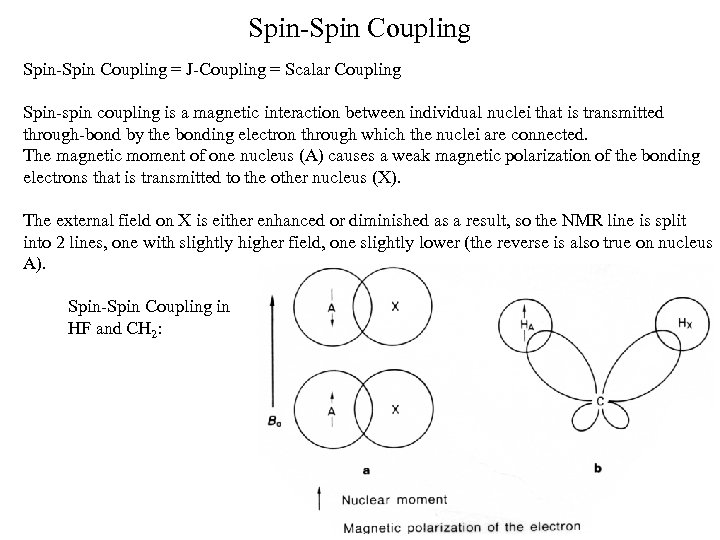
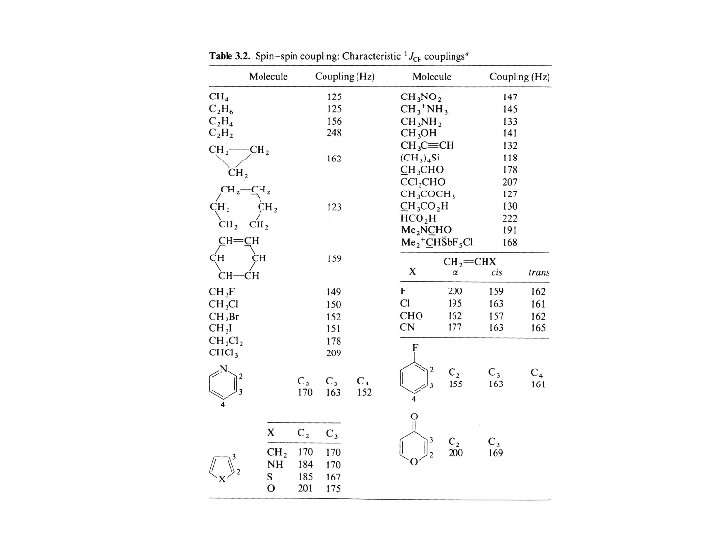
Spin-Spin Coupling = J-Coupling = Scalar Coupling Spin-spin coupling is a magnetic interaction between individual nuclei that is transmitted through-bond by the bonding electron through which the nuclei are connected. The magnetic moment of one nucleus (A) causes a weak magnetic polarization of the bonding electrons that is transmitted to the other nucleus (X). The external field on X is either enhanced or diminished as a result, so the NMR line is split into 2 lines, one with slightly higher field, one slightly lower (the reverse is also true on nucleus A). Spin-Spin Coupling in HF and CH 2:

Scalar Coupling Constant The energy of the spin states is given by: E = JAXIAIX E is the energy of the interaction IA and IX are nuclear spin vectors of the two nuclei JAX is the scalar coupling constant. From this equation, the magnetic field does not affect the value of the JAX term. The units for JAX are Hz. Thus, a scalar coupling constant of 1 Hz on an 800 MHz spectrometer is still 1 Hz on a 200 MHz spectrometer.

Energy Level Diagram for Spin-Spin Coupling Two spins have 4 possible orientations with respect to the magnetic field- both parallel, antiparallel, one parallel/one antiparallel and the reverse. If there is J-coupling between A and X, then the states are stabilized or destabilized. The energy difference for each state is: Thus, the energy difference of the transition is: E 1 = 1/2 A + 1/2 X + 1/4 JAX E 2 = 1/2 A - 1/2 X - 1/4 JAX E 3 = -1/2 A + 1/2 X - 1/4 JAX E 4 = -1/2 A - 1/2 X + 1/4 JAX E 1 - E 3 = A + 1/2 JAX E 2 - E 4 = A - 1/2 JAX E 1 - E 2 = X + 1/2 JAX E 3 - E 4 = X - 1/2 JAX

Interpreting Multiplets 1. The multiplicity of the splitting is (2 n. I +1) where n is the number of nuclei in the neighboring group, assuming that the chemical shift is >> than the coupling constant, the coupling constants are all equivalent, and nuclei are spin = 1/2. 2. The line separation in Hz is the coupling constant between the two nuclei. 3. The relative intensities within a multiplet can be read from Pascals triangle: 4. The splitting patterns are independent of the sign of the coupling constant (even number coupling constants can be negative- 2 bond, 4 bond. . . ). 5. Scalar coupling is not restricted to nuclei 2 or 3 bonds apart, but coupling constants decrease in magnitude (approximately) as the two nuclei become further away through-bond. As the coupling constant becomes smaller, the ability to resolve them becomes less, as the linewidth of the detected nucleus must be < than the coupling constant to resolve the coupling.

Geminal Coupling Constants 2 J(H, H) 1) H-C-H Bond Angle 2) Hybridization of the Carbon atom 3) Substituents 2 J(H, H) Normally negative Magnitude ~0 -30 Hz; commonly 0 -12 Hz

Vicinal Coupling Constants Martin Karplus determined the correlation between 3 -bond J-coupling (3 J) constant (vicinal coupling) and torsion angle. The rough approximation is that the 3 J is proportional to the cos 2 where is the torsion angle. 3 J (or vicinal coupling constant) depends upon: 1) Dihedral Angle 2) C-C bond length 3) H-C-C valence angles 4) Substituents, especially electronegativity of the R substituent on the H-C-C-H moiety 4 -bond coupling constants also depend upon torsion angle, except they depend upon 2 torsion angles. The formula for 4 J is proportional to cos 2 where and are the two angles. The correlation between 3 J and 4 J and torsion angle applies to not only proton-proton coupling constants but also heteronuclear coupling constants as well.

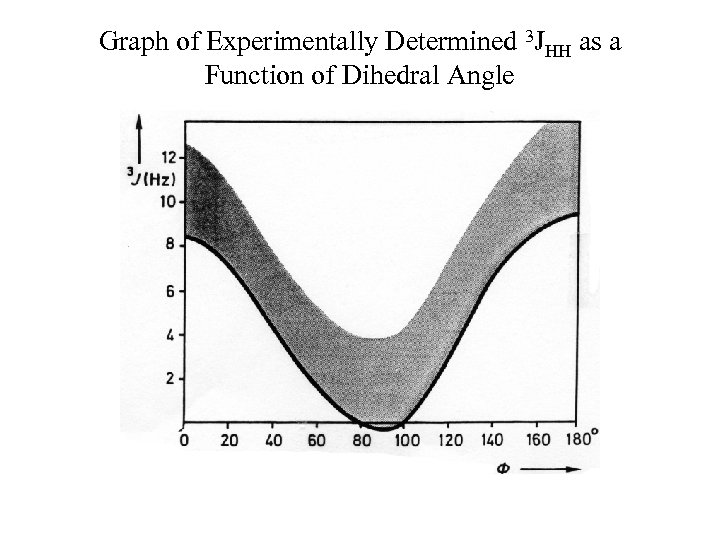
Graph of Experimentally Determined 3 JHH as a Function of Dihedral Angle

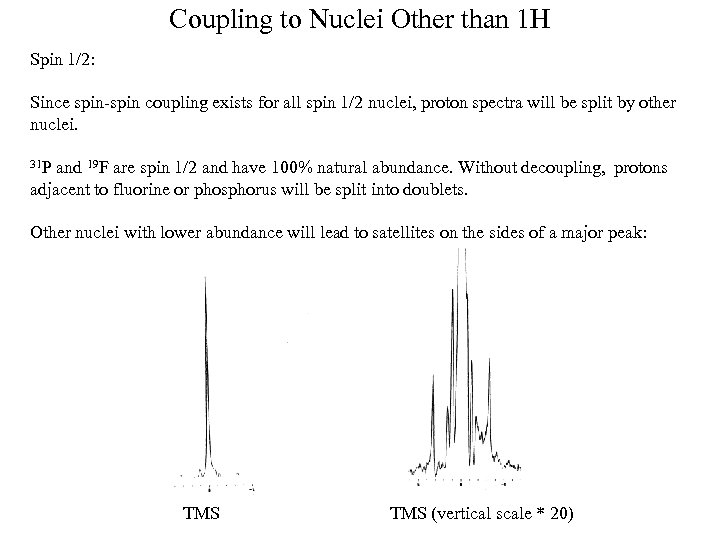
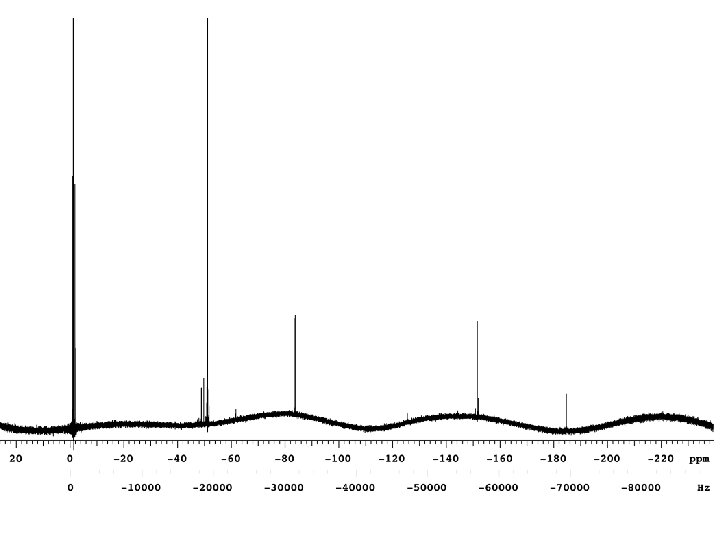
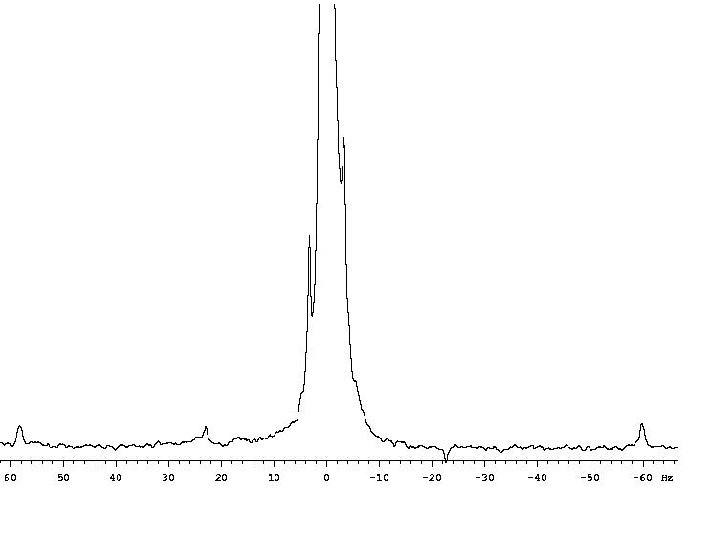
Coupling to Nuclei Other than 1 H Spin 1/2: Since spin-spin coupling exists for all spin 1/2 nuclei, proton spectra will be split by other nuclei. 31 P and 19 F are spin 1/2 and have 100% natural abundance. Without decoupling, protons adjacent to fluorine or phosphorus will be split into doublets. Other nuclei with lower abundance will lead to satellites on the sides of a major peak: TMS (vertical scale * 20)

Spin-Spin Coupling to Quadrupolar Nuclei (Spin > 1/2) Spin > 1/2 nuclei split spin 1/2 nuclei into different multiplets than spin 1/2 nuclei. The multiplicity of a resonance is given by 2 n. I +1 where n is the number of neighboring nuclei and I is the spin. Why is the 13 C of CDCl 3 not further split by 35 Cl or 37 Cl (both I = 3/2)? Deuterium is also quadrupolar, why is splitting to it observed? The quadrupole moment is less for deuterium; see Table from first lecture. Is there a way to observe coupling to quadrupolar nuclei that is not normally observed?

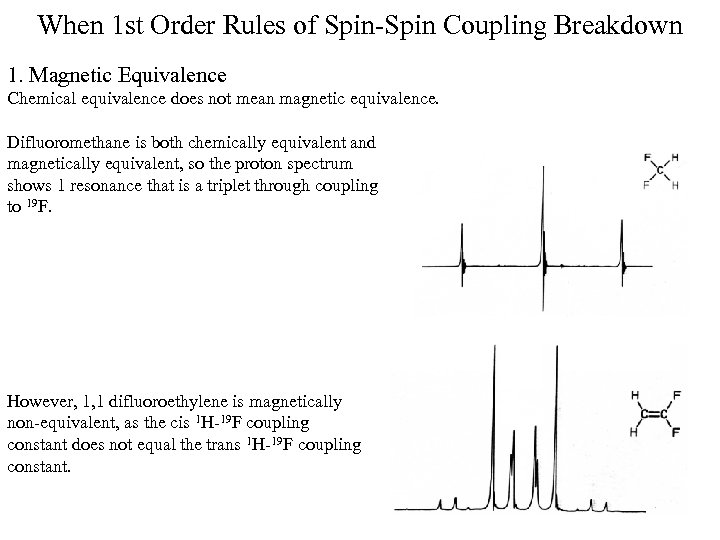
When 1 st Order Rules of Spin-Spin Coupling Breakdown 1. Magnetic Equivalence Chemical equivalence does not mean magnetic equivalence. Difluoromethane is both chemically equivalent and magnetically equivalent, so the proton spectrum shows 1 resonance that is a triplet through coupling to 19 F. However, 1, 1 difluoroethylene is magnetically non-equivalent, as the cis 1 H-19 F coupling constant does not equal the trans 1 H-19 F coupling constant.

2. Chemical shift (in Hz) is not >> coupling constant. If the chemical shift in Hz is similar to the coupling constant, extra lines will be observed Extra lines indicate higher order splitting pattern. In higher order splitting spectra, sign of the coupling constants do affect spectra unlike in normal 1 st order splitting patterns.

Spin Systems A spin-system is a group of n nuclei that have I = 1/2, with no more n resonance frequencies and n(n - 1)/2 coupling constants; this group does not interact magnetically with any other nuclei. Nomenclature: Nuclei of the same chemical shift are noted with the same capital letter, with a subscript of the amount of nuclei, for example a methyl would be A 3. If the chemical shift of another group that is coupled to the A 3 is similar, such as an ethyl group, the next letter in the alphabet is used; thus, an ethyl is A 3 B 2. For groups far apart in chemical shift, the other side of the alphabet is used; thus, a CH 3 CF 2 group would be A 3 X 2. When nuclei are magnetically non-equivalent but have the same chemical shift (see difluoroethylene above), primes are used; thus, difluoroethylene is AA'XX'. For three nuclei not close in chemical shift, the nomenclature would be AMX.

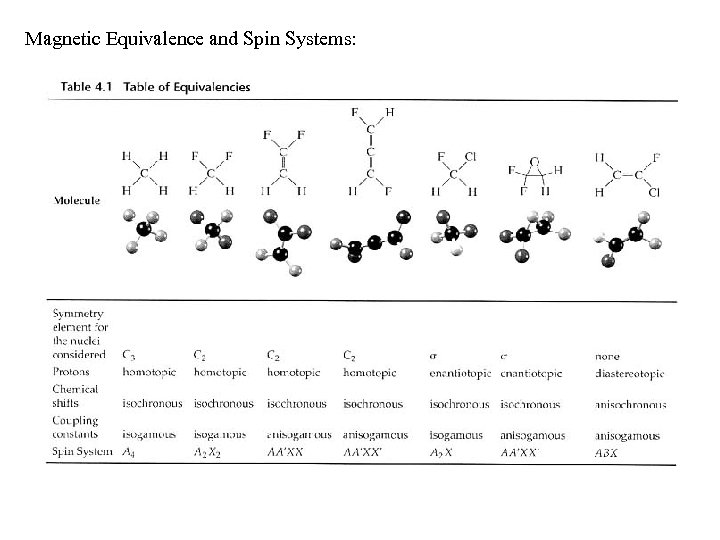
Magnetic Equivalence and Spin Systems:

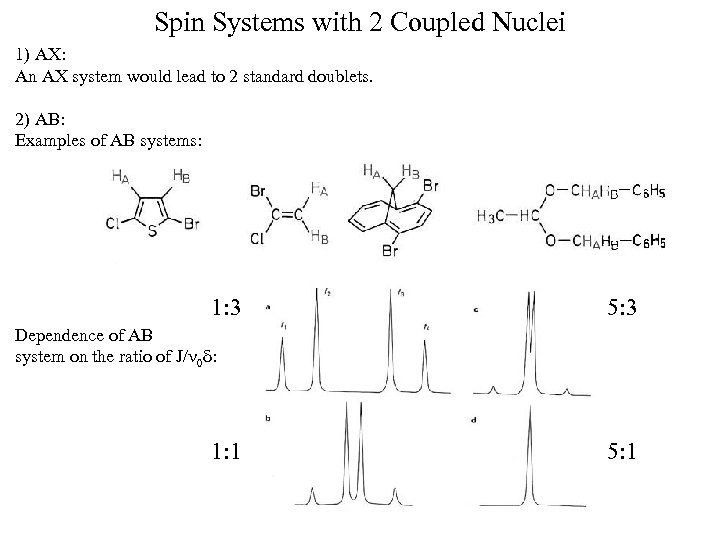
Spin Systems with 2 Coupled Nuclei 1) AX: An AX system would lead to 2 standard doublets. 2) AB: Examples of AB systems: 1: 3 5: 3 Dependence of AB system on the ratio of J/ 0 : 1: 1 5: 1

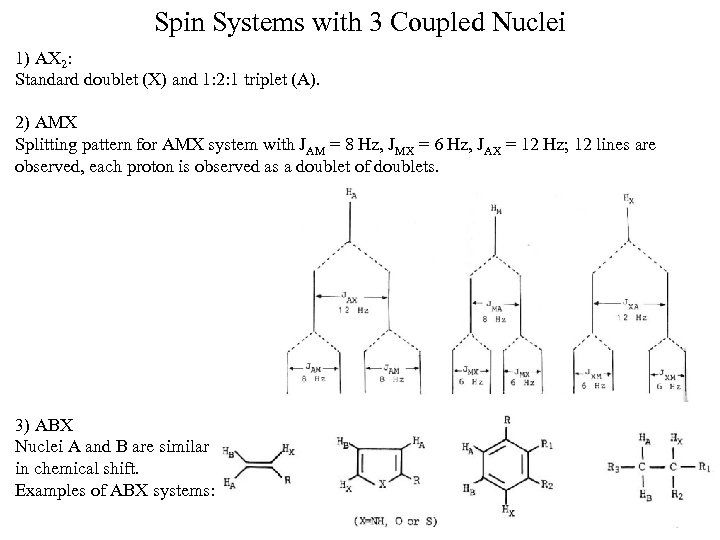
Spin Systems with 3 Coupled Nuclei 1) AX 2: Standard doublet (X) and 1: 2: 1 triplet (A). 2) AMX Splitting pattern for AMX system with JAM = 8 Hz, JMX = 6 Hz, JAX = 12 Hz; 12 lines are observed, each proton is observed as a doublet of doublets. 3) ABX Nuclei A and B are similar in chemical shift. Examples of ABX systems:

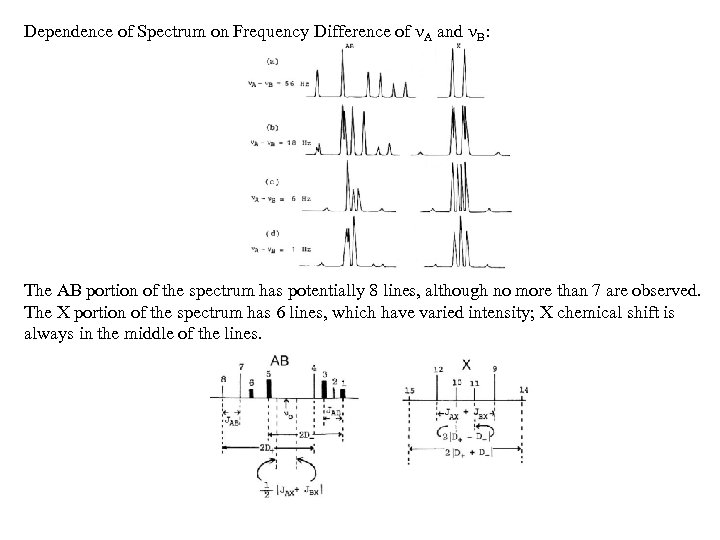
Dependence of Spectrum on Frequency Difference of A and B: The AB portion of the spectrum has potentially 8 lines, although no more than 7 are observed. The X portion of the spectrum has 6 lines, which have varied intensity; X chemical shift is always in the middle of the lines.

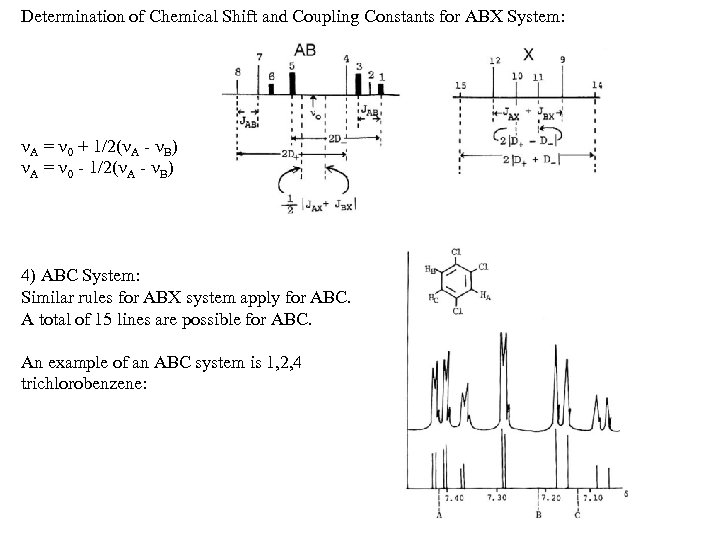
Determination of Chemical Shift and Coupling Constants for ABX System: A = 0 + 1/2( A - B) A = 0 - 1/2( A - B) 4) ABC System: Similar rules for ABX system apply for ABC. A total of 15 lines are possible for ABC. An example of an ABC system is 1, 2, 4 trichlorobenzene:

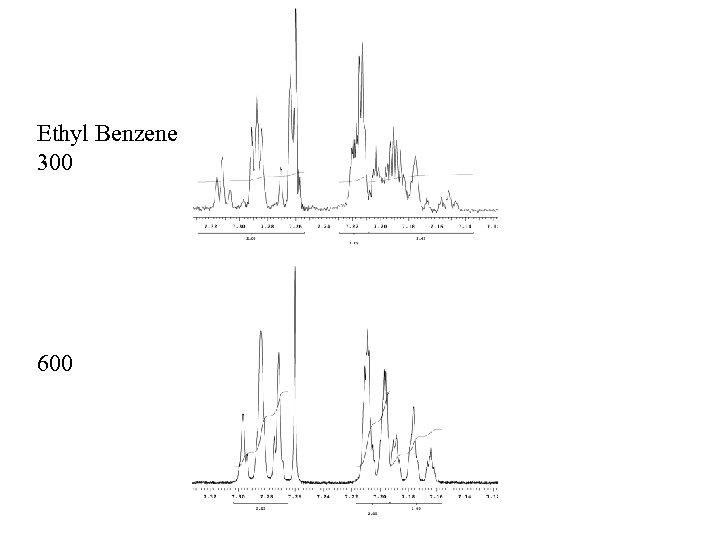
Ethyl Benzene 300 600