NLP Parsing and more Grammar Topics DCG recognisor

NLP: Parsing and more Grammar Topics: DCG recognisor • two implementations Parsing • Parse tree • DCG recognisor with grammar features

A Simple Grammar S NP VP VP V NP NP Proper_N NP det N Proper_N John Proper_N Mary N cake V loves V ate det the Sentences in this language: “John loves Mary” “John ate the cake” “John loves the cake”

Definite Clause Grammars (DCGs) The above grammar can be simply implemented in DCG notation as follows: s --> np, vp. vp --> v, np. np --> proper_n. np --> det, n. proper_n --> [john]. proper_n --> [mary]. n --> [cake]. v --> [loves]. v --> [ate]. det --> [the].

Translating DCG Consider the rule s --> np, vp. Prolog translates this as: s(Ws 1, Ws 2) : - np(Ws 1, Ws), vp(Ws, Ws 2). This says that after taking an s off the start of Ws 1, Ws 2 remains The rule proper_n --> [john]. is translated as proper_n([john|Ws], Ws). Query • s([john, ate, the cake], []). • Yes • s([ate, john, cake, the], []). • No

A Second Implementation A more efficient implementation: s --> np, vp. vp --> [V], {verb(V)}, np. np --> [N], {proper_n(N)}. np --> [Det], {det(Det)}, [N], {noun(N)}. proper_n(john). proper_n(mary). noun(cake). verb(loves). verb(ate). det(the). Notes: 1. The {} allow Prolog code to be embedded in DCG rules 2. The cost of processing is now less dependent on lexicon size (given good indexing) 3. So far we have implemented only a DCG recogniser, not a parser.

Parsing Consider the goal s([john, ate, the, cake], []) It will have the following parse/proof tree s np vp proper_n v [john] [ate] np det n [the] [cake] How to represent a tree in Prolog?

A DCG Parser We can include extra arguments on nonterminals in our grammar, these allow us to record the parse tree: s(s(NP, VP)) --> np(NP), vp(VP). vp(vp(verb(V), NP)) --> [V], {verb(V)}, np(NP). np(np(proper_n(N))) --> [N], {proper_n(N)}. np(np(det(Det), noun(N))) --> [Det], {det(Det)}, [N], {noun(N)}.

A DCG Parser (ctd. ) Arguments to DCG non-terminals are expanded by Prolog like this: s(s(NP, VP), Ws 1, Ws 2) : np(NP, Ws 1, Ws), vp(VP, Ws 2). Here, arguments are used to build up a parse tree: ? - s(Parse, [john, ate, the, cake], []). Parse = s(np(proper_n(john)), vp(verb(ate), np(det(the), noun(cake))))

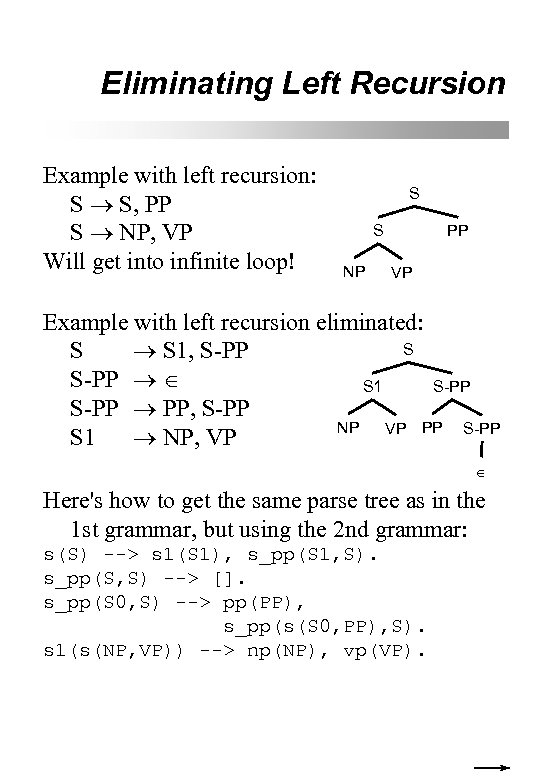Eliminating Left Recursion Example with left recursion: S S, PP S NP, VP Will get into infinite loop! S S NP PP VP Example with left recursion eliminated: S S S 1, S-PP S 1 S-PP PP, S-PP NP VP PP S-PP S 1 NP, VP Here's how to get the same parse tree as in the 1 st grammar, but using the 2 nd grammar: s(S) --> s 1(S 1), s_pp(S 1, S). s_pp(S, S) --> []. s_pp(S 0, S) --> pp(PP), s_pp(s(S 0, PP), S). s 1(s(NP, VP)) --> np(NP), vp(VP).

Grammatical vs Ungrammatical sentences ungrammatical (syntactically incorrect) sentences – – – The John eats the hamburger. John eat the hamburger. John died Mary. A hostages ate the hamburgers. Him ate him. syntactically correct sentences: – – – John eats the hamburger. The people eat the hamburgers. Hostages eat hamburgers. Hamburgers killed Jim. Cholesterol killed Jim.

Some Grammatical Features. We can use the idea of grammatical features to solve this problem: • Number: singular, plural: hamburger, hamburgers • Person: 1 st, 2 nd, or 3 rd: eat, eats • Proper noun: true or false: John, hamburger • Mass noun: true (bread) or false (bun): compare “a bread” & “a bun” • Transitivity: transitive or intransitive: give, die • Case: subjective (I, he, she, they), objective (me, him, her, them)

Modifying a DCG to handle case subjective objective I me you he him she her it it they them Examples He saw her. She saw him. You gave it to me. I gave them to you. They gave it to them. They gave them it. s --> np_sub, vp. vp --> v, np_obj. vp --> v. pp --> prep, np_obj -> pro_obj. np_obj -> det, n. np_sub -> pro_sub. np_sub -> det, n. pro_sub --> [i]. pro_sub --> [you]. pro_sub --> [he]. pro_sub --> [she]. pro_obj --> [me]. pro_obj --> [you]. pro_obj --> [him]. pro_obj --> [her].

Augmenting a DCG to handle case There are other grammatical features we need to match, and if we keep making more specialized grammar rules, we will end up with exponential number of rules. Alternative is to augment grammar. s --> np(sub), vp. vp --> v, np(obj). vp --> v. pp --> prep, np(obj). np(Case) -> pro(Case). np(_) --> det, n. pro(Case) -> [Pro], {pro(Pro, Case)}. % Lexical entries: pro(i, sub). pro(you, sub). pro(he, sub). pro(she, sub). pro(me, obj). pro(you, obj). pro(him, obj). pro(her, obj).

Subject-verb agreement In English, number and person of the subject must agree with the verb: “I am” / “she is” / “they are” Person Number Pronoun Verb examples… ––––––––––––––––––––– 1 st sing I eat am have 2 nd– you eat are have 3 rd sing he/she/it eats is has 1 st plur we eat are have 3 rd plur they eat are have

Implementing subject-verb agreement Can combine checking subject-verb agreement in person/number with case checking: % subject must agree with verb s --> np(Per, Num, sub), vp(Per, Num). % person and number of object doesn’t matter vp(Per, Num) --> v(Per, Num), np(_, _, obj). vp(Per, Num) --> v(Per, Num). % look up V, retrieve its person and number v(Per, Num) --> [V], {v(V, Per, Num)}. % person, number and case comes from pronoun np(Per, Num, Case) --> pro(Per, Num, Case). % look up person, number and case of pronoun pro(Per, Num, Case) --> [Pro], {pro(Pro, Per, Num, Case)}. % lexical entries pro(she, second, sing, obj). v(eats, third, sing).

Agreement for nouns & determiners Articles (a type of determiner) have restrictions based on number and whether the noun is mass or count Article Number Def/Indef Example ––––––––––––––––––– a/an singular indefinite a man saw … plural indefinite men saw… the singular definite the man saw … the plural definite the men saw… Mass nouns (bread, money, water) take no article when used in the indefinite, and go with a verb in the singular

Determiners can be quite complicated: can involve numbers (& many other things) Definite Indefinite –––––––––––––– the dog a dog the red dogs blue dogs the three dogs my uncle Bob’s friend’s dog every pink large dog all but three of the red dogs Proper nouns take no determiners

Noun/determiner agreement Mass nouns Count nouns –––––––––––––––––– the bread tastes good. the loaf tastes good. *a bread taste good. (don’t use indef article with mass nouns) bread tastes good. a loaf tastes good. *bread taste good loaves taste good. (mass nouns go with sing. verb) *the three bread … the three loaves cost $4 *three bread … three loaves cost $4 (can’t use numbers with mass nouns) the money is heavy. money buys power. the coins are heavy. the coin is heavy. a coin buys … coins buy icecreams

DCG rules for noun/determiner agreement % Proper nouns are noun-phrases np(Number, _Person, _Case) --> proper_n(Number, _). % Mass nouns need no determiners np(sing, _Person, _Case) --> n 1(sing, mass). % Determiner-Noun (can’t have indef % determiner + mass noun) np(Number, _, _) --> det(Number, Definite), n 1(Number, Mass), {+ (Mass=mass, Definite=indef)}. n 1(Number, Mass) --> adj, n 1(Number, Mass) --> n(Number, Mass).

DCG rules for noun/ determiner agreement (ctd) n(Number, Mass) --> [N], {noun(N, Number, Mass)}. proper_n(Number, Mass) --> [N], {proper_noun(N, Number, Mass)}. det(Number, Definite) --> [], {det([], Number, Definite)}. det(Number, Definite) --> [Det], {det(Det, Number, Definite)}. adj --> [Adj], {adj(Adj)}. proper_noun(john, sing, count). noun(loaf, sing, count). noun(loaves, plur, count). noun(bread, sing, mass). det(a, sing, indef). det([], plur, indef). det(the, _, def). adj(three). adj(large).