Ніяке людське дослідження не може називатися справжнім знанням

"Ніяке людське дослідження не може називатися справжнім знанням, якщо воно не пройшло через математичні доведення". Леонардо да Вінчі

Тема 4 ПРЕДМЕТ МАТЕМАТИЧНОГО ПРОГРАМУВАННЯ 1. Постановка задачі математичного програмування 2. Класифікація задач математичного програмування 3. Типові задачі лінійного програмування 4. Форми запису задачі лінійного програмування

А. Г. Аганбегян Н. П. Бусленко Є. С. Вентцель Н. Н. Воробйов Б. В. Гнєденко Т. І. Заславська Л. В. Канторович А. Л. Лур’є Н. Н. Моісеєв В. С. Нємчінов А. Т. Тіхонов Н. П. Федоренко Д. Б. Юдін Р. Акоф Р. Белман Г. Данциг Г. Кун Дж. фон Нейман Т. Сааті Р. Черчмен А. Кофман

Постановка задачі математичного програмування Математичне програмування ‑ це сукупність методів прийняття оптимальних рішень на основі знаходження екстремумів функцій багатьох змінних за наявності обмежень на ці змінні. Характерною особливістю задач математичного програмування є те, що оптимальне значення числової функції f, зазвичай, досягається на межі множини D, тому використати класичні методи пошуку екстремуму функції при розв’язанні таких задач практично неможливо.

Класифікація задач МП

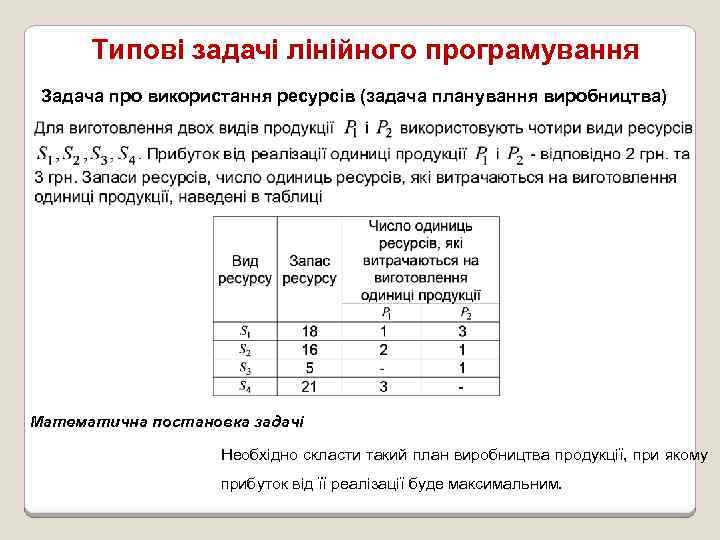Типові задачі лінійного програмування Задача про використання ресурсів (задача планування виробництва) Математична постановка задачі Необхідно скласти такий план виробництва продукції, при якому прибуток від її реалізації буде максимальним.

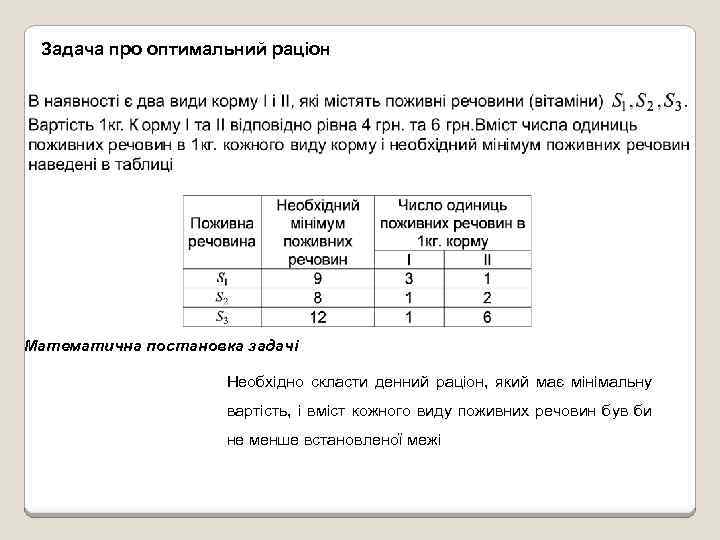Задача про оптимальний раціон Математична постановка задачі Необхідно скласти денний раціон, який має мінімальну вартість, і вміст кожного виду поживних речовин був би не менше встановленої межі

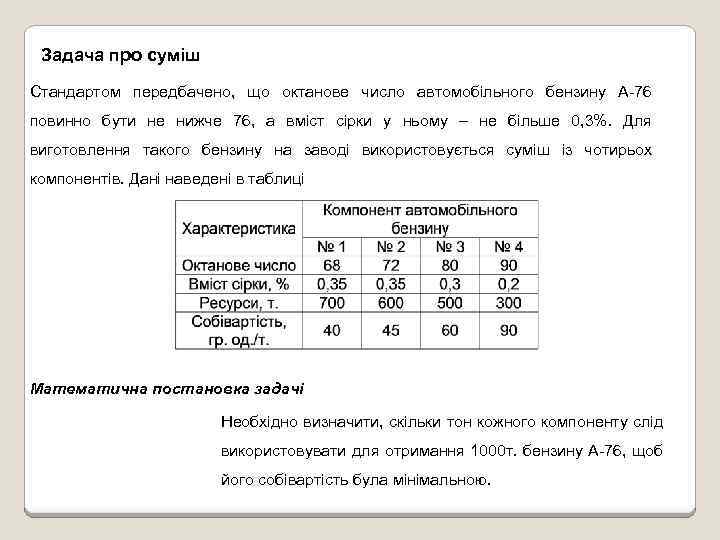Задача про суміш Стандартом передбачено, що октанове число автомобільного бензину А-76 повинно бути не нижче 76, а вміст сірки у ньому – не більше 0, 3%. Для виготовлення такого бензину на заводі використовується суміш із чотирьох компонентів. Дані наведені в таблиці Математична постановка задачі Необхідно визначити, скільки тон кожного компоненту слід використовувати для отримання 1000 т. бензину А-76, щоб його собівартість була мінімальною.

Задача оптимального розкрою (максимум комплектів розкрою) Для виготовлення брусів довжиною 1, 2 м. , 3 м. і 5 м. у відношенні 2 : 1 : 3 на розпил поступає 195 колод довжиною 6 м. Математична постановка задачі Визначити план розпилу, який забезпечує максимальне число комплектів. Визначимо всі можливі способи розпилу колод, вказавши відповідне число отриманих при цьому брусів

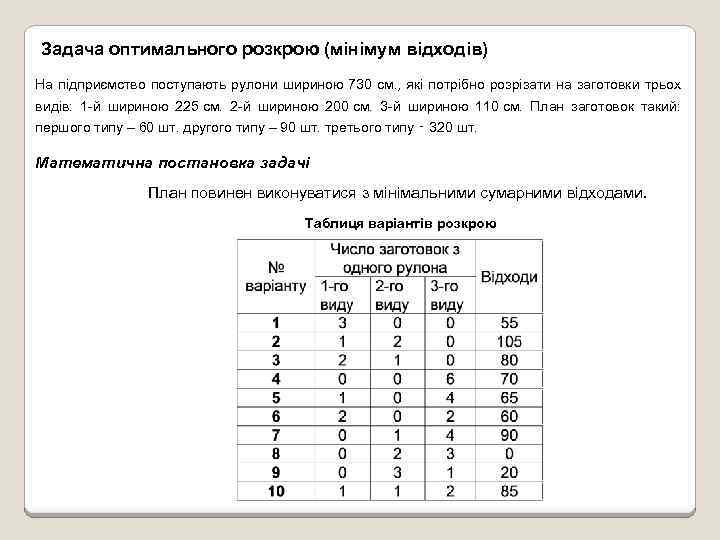Задача оптимального розкрою (мінімум відходів) На підприємство поступають рулони шириною 730 см. , які потрібно розрізати на заготовки трьох видів: 1 -й шириною 225 см. 2 -й шириною 200 см. 3 -й шириною 110 см. План заготовок такий: першого типу – 60 шт. другого типу – 90 шт. третього типу ‑ 320 шт. Математична постановка задачі План повинен виконуватися з мінімальними сумарними відходами. Таблиця варіантів розкрою

Транспортна задача . У кожного із постачальників накопичено відповідно 300, 250, 110 одиниць товару. Потреби споживачів складають відповідно 100, 200, 150, 210 одиниць товару. Вартості перевезення товару від i-го постачальника до j-го споживача подано у вигляді матриці, яку називають матрицею тарифів: В даному випадку маємо транспортну задачу з правильним балансом, тобто обсяги потреб та запасів рівні: 100 + 200 + 150 + 210 = 300 + 250 +110 = 600 Математична постановка задачі

Позначимо xij - кількість товару, перевезеного від i-го постачальника до j-го. Cформуємо умову задачі у вигляді таблиці.

Форми запису задачі лінійного програмування (ЗЛП) 1. Загальна 2. Стандартна (симетрична) 3. Канонічна (основна)

1. Загальна форма ЗЛП

22

2. Стандартна (симетрична) форма ЗЛП 23

3. Канонічна (основна) форма ЗЛП Будь-яка ЗЛП може бути зведена до канонічної, стандартної чи загальної форми 24

ДЛЯ ПЕРЕХОДУ ВІД ОДНІЄЇ ФОРМИ ЗАПИСУ ЗЛП ДО ІНШОЇ, НЕОБХІДНО ВМІТИ: 25