Newton s Universal Law of Gravity and Satellite Motion

Newton’s Universal Law of Gravity and Satellite Motion

Newton and Gravity There is a popular story that Newton was sitting under an apple tree, an apple fell on his head, and he suddenly thought of the Universal Law of Gravitation. As in all such legends, this is almost certainly not true in its details, but the story contains elements of what actually happened

Newton Isaac Newton, formulated a theory of gravity. Legend has it that he was prompted by watching an apple fall. Newton speculated that the same force that caused object to drop to the ground was responsible for the moon’s orbit. Newton knew an apple falls 4. 9 m in one second. He calculated the moon to fall 1. 4 mm in one second. The moon was known to be 60 times further from the center of the Earth than the surface of the Earth. It was reasonable to suggest that the force was a function of the distance between objects.

Moon and Apple Note that 4. 9 m/60 = 8. 2 cm, but 4. 9 m/3600 = 1. 4 mm which is the distance Newton calculated the Moon would fall in one second. Thus, he reasoned, force would have to be proportional to the inverse square of the distance between the two objects Fgrav α 1 / d 2

Universal Law of Gravitation Gravity is universal and everything is pulling on every other object, gravity is an “attractive” force. Newton’s Law states that the gravitational force between two objects is directly proportional to the mass of the objects and inversely proportional to the square of the distance between the objects center of mass. F ~ m 1 m 2/d 2

Newton

Gravitational Constant • The proportionality form of the law can be expressed as an exact equation by introducing a proportionality constant, the universal gravitational constant. • F = Gm 1 m 2/d 2 G = 6. 67 X 10 -11 N-m 2/kg 2 G was first measured 150 years after Newton proposed his law by Henry Cavendish.

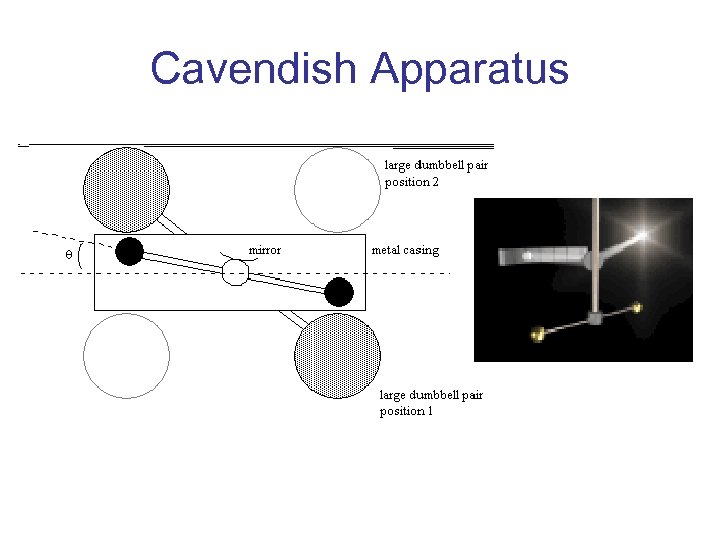Cavendish Apparatus

Weighing the Earth • Cavendish’s determination of the gravitational constant determined the mass of the Earth (since the radius was known) • F = GMEarthm/d 2 =mg 9. 8 m/s 2 = 6. 67 X 10 -11 MEarth/(6400000 m)2 MEarth = 6 X 1024 kg

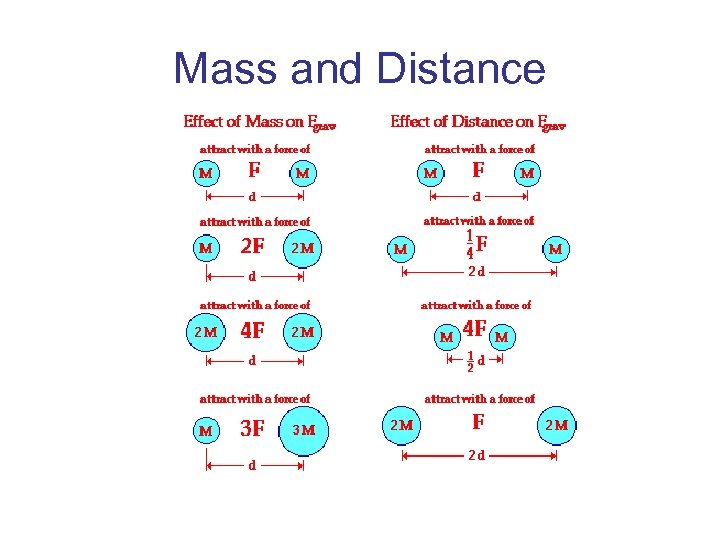Mass and Distance

Need large masses • The fact that G is so small tells us that the gravitational force is small between most objects Two 2, 000 kg objects are 1 meter apart F = 6. 67 X 10 -11 X(2000)2/(1 m)2 =0. 00013 N

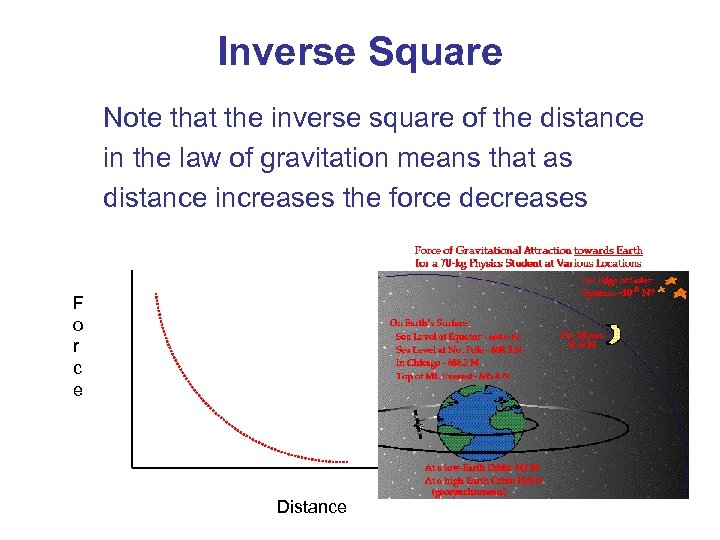Inverse Square Note that the inverse square of the distance in the law of gravitation means that as distance increases the force decreases F o r c e Distance

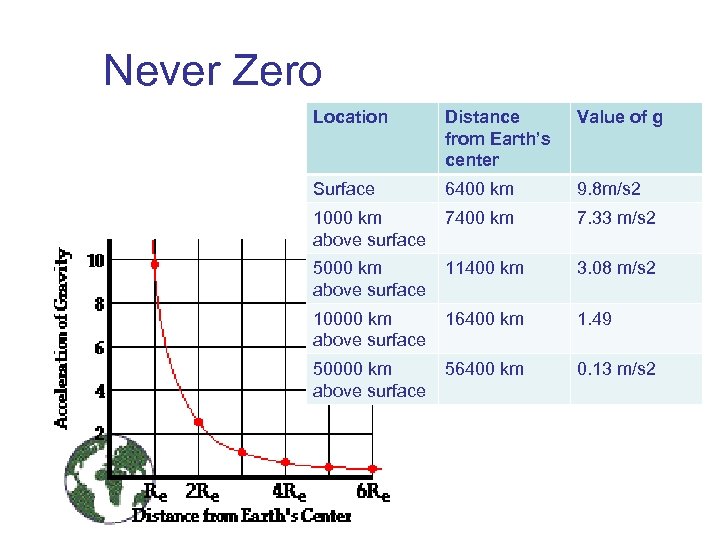Never Zero Location Distance from Earth’s center Value of g Surface 6400 km 9. 8 m/s 2 1000 km above surface 7400 km 7. 33 m/s 2 5000 km above surface 11400 km 3. 08 m/s 2 10000 km above surface 16400 km 1. 49 50000 km above surface 56400 km 0. 13 m/s 2

Gravity Business • Having recently completely mastering the Newton’s law of gravitation, Hillary has devised a new business plan. Hillary learned that objects weigh different amounts at different distances from Earth's center. Her plan involves buying gold by the weight at one altitude and then selling it at another altitude at the same price per weight. Should Hillary buy at a high altitude and sell at a low altitude or vice versa? • To succeed Hillary must buy High and sell Low (altitude)… note this is the opposite of the goal on Wall street where all investors want to buy low and sell high.

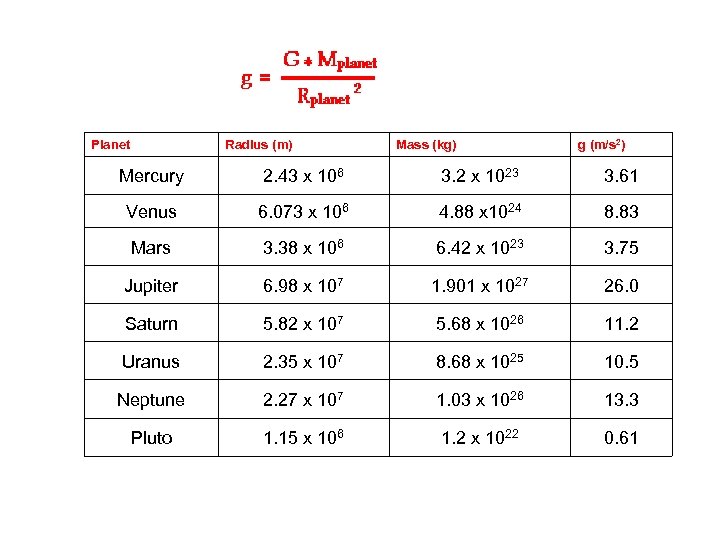Planet Radius (m) Mass (kg) g (m/s 2) Mercury 2. 43 x 106 3. 2 x 1023 3. 61 Venus 6. 073 x 106 4. 88 x 1024 8. 83 Mars 3. 38 x 106 6. 42 x 1023 3. 75 Jupiter 6. 98 x 107 1. 901 x 1027 26. 0 Saturn 5. 82 x 107 5. 68 x 1026 11. 2 Uranus 2. 35 x 107 8. 68 x 1025 10. 5 Neptune 2. 27 x 107 1. 03 x 1026 13. 3 Pluto 1. 15 x 106 1. 2 x 1022 0. 61

From Newton to Einstein • General relativity or the General theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1915/16. It unifies special relativity and Newton's law of universal gravitation, resulting in a theory in which gravity is a property of the geometry of space and time. • Einstein himself had shown in 1915 how it explained the anomalous perihelion advance of the planet Mercury and a 1919 expedition led by Eddington had announced confirmation of general relativity's prediction for the deflection of the light of distant stars by the Sun (instantly catapulting Einstein to world fame.

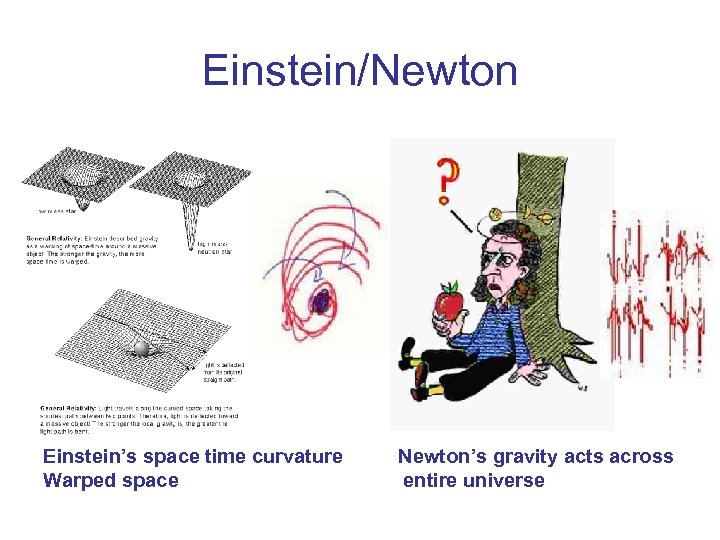Einstein/Newton Einstein’s space time curvature Newton’s gravity acts across Warped space entire universe

Precession of Mercury • An early success of general relativity was that theory offered a straightforward explanation for an anomalous perihelion shift of the planet Mercury, which had been discovered in 1859 but had remained mysterious. This agreement between theory and experiment confirmed for Einstein that he had at last identified the correct form of the gravitational field equations.

Lensing • A grid of points (see expanded image), representing background quasars, is gravitationally lensed by a foreground galaxy.

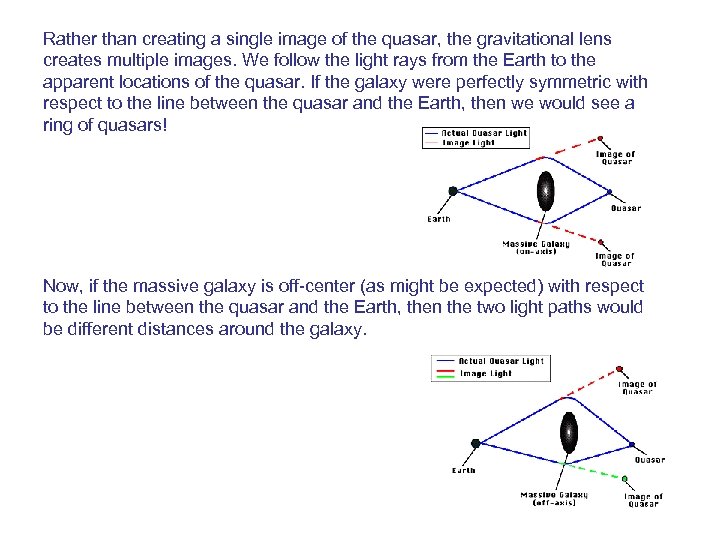Rather than creating a single image of the quasar, the gravitational lens creates multiple images. We follow the light rays from the Earth to the apparent locations of the quasar. If the galaxy were perfectly symmetric with respect to the line between the quasar and the Earth, then we would see a ring of quasars! Now, if the massive galaxy is off-center (as might be expected) with respect to the line between the quasar and the Earth, then the two light paths would be different distances around the galaxy.

Gravitational Lensing • The deflection of light by gravity can have an intriguing side effect: a massive object between the observer and a distant target object makes it possible for the observer to see multiple distorted images of the target. This and similar effects are known as gravitational lensing.

Einstein General Relativity • There are questions for which even Einstein had no answers. For example, if gravity is a force that causes all matter to be attracted to all other matter, why are atoms mostly empty space inside? (There is really hardly any actual matter in an atom!) How are the forces that hold atoms together different from gravity? Is it possible that all the forces we see at work in nature are really different sides of the same basic force or structure?

Satellites • When you drop something it falls straight down, when you throw something it follows a curved path. The larger the horizontal velocity the further it travels before it hits the ground. • Is it possible to throw it fast enough that it will not hit the ground?

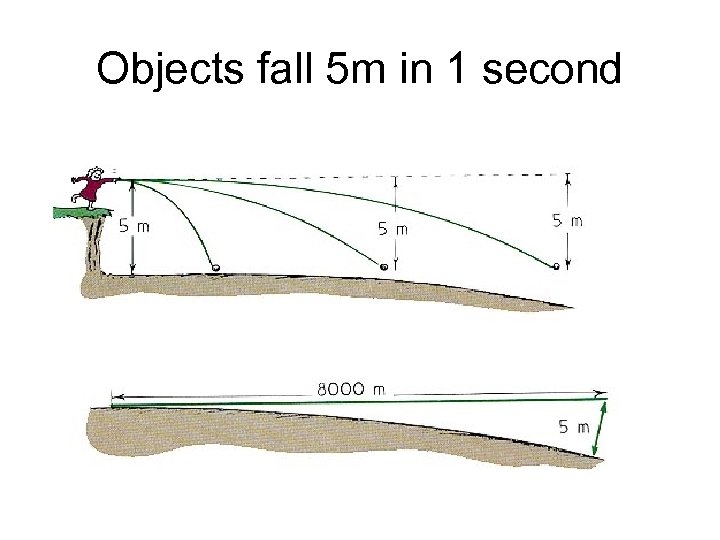Objects fall 5 m in 1 second

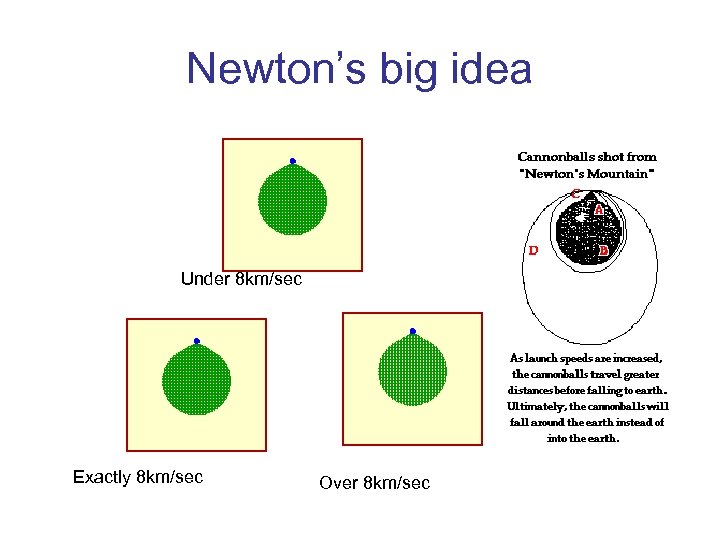Newton’s big idea Under 8 km/sec Exactly 8 km/sec Over 8 km/sec

Satellites • Satellites typically orbit ~150 mile above the surface of the Earth to avoid friction from the atmosphere • Satellites close to the Earth complete an orbit in approximately 90 minutes, at higher altitudes the velocity decreases and the circumference of the orbit is longer so the period increases.

Sputnik History changed on October 4, 1957, when the Soviet Union successfully launched Sputnik I. The world's first artificial satellite was about the size of a basketball, weighed only 183 pounds, and took about 98 minutes to orbit the Earth on its elliptical path. That launch ushered in new political, military, technological, and scientific developments. While the Sputnik launch was a single event, it marked the start of the space age and the U. S. -U. S. S. R space race. http: //history. nasa. gov/sputnik. wav

Satellites in Circular path •

Satellites in circular orbit • Circumference of orbit is 2πr • The frequency of revolution is speed/circumference or v/2πr • The period of revolution is 1/f, or 2πr/v • T = 2πr/√(GMe/r)

Elliptical orbits • Satellites and planets actually follow elliptical orbits. Elliptical orbits occur when the velocity is greater than 8000 m/s and less than the escape velocity • The celestial body being orbited is located at one of the foci of the elliptical path • Note the Centripetal force is supplied by gravity

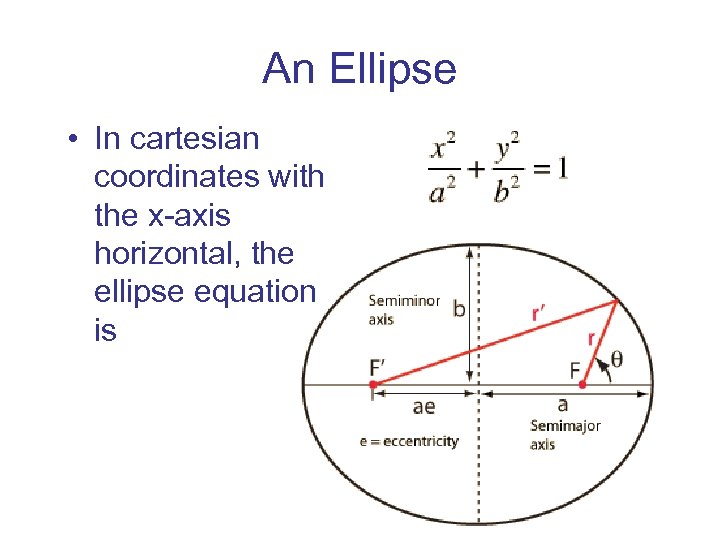An Ellipse • In cartesian coordinates with the x-axis horizontal, the ellipse equation is

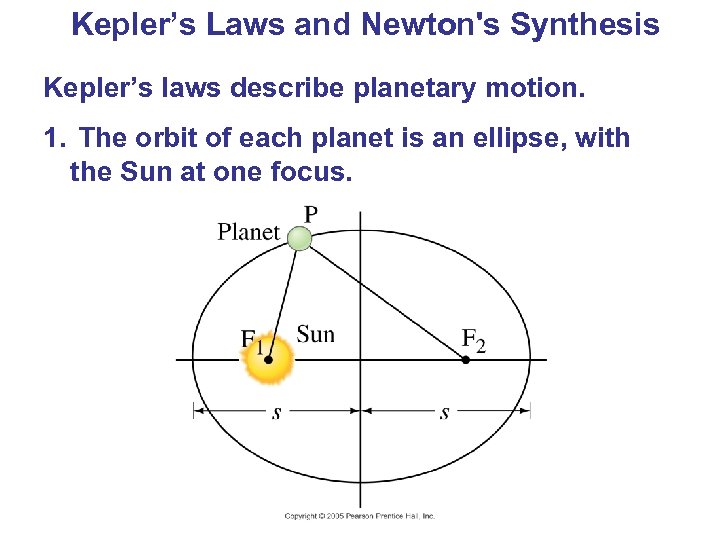Kepler’s Laws and Newton's Synthesis Kepler’s laws describe planetary motion. 1. The orbit of each planet is an ellipse, with the Sun at one focus.

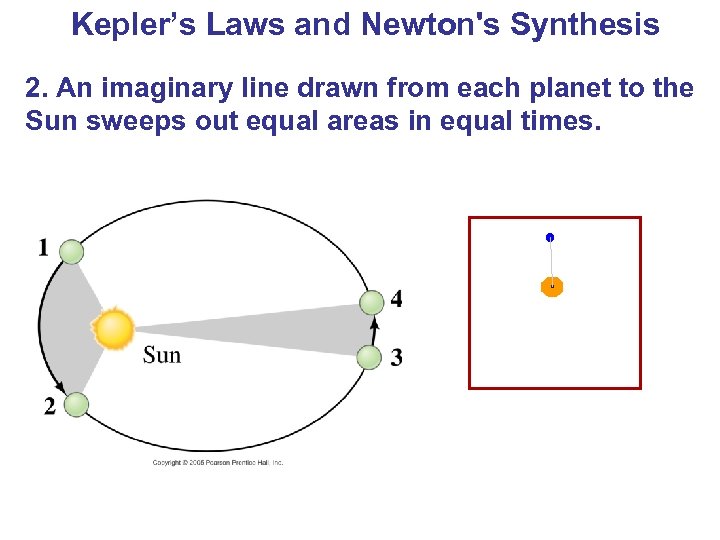Kepler’s Laws and Newton's Synthesis 2. An imaginary line drawn from each planet to the Sun sweeps out equal areas in equal times.

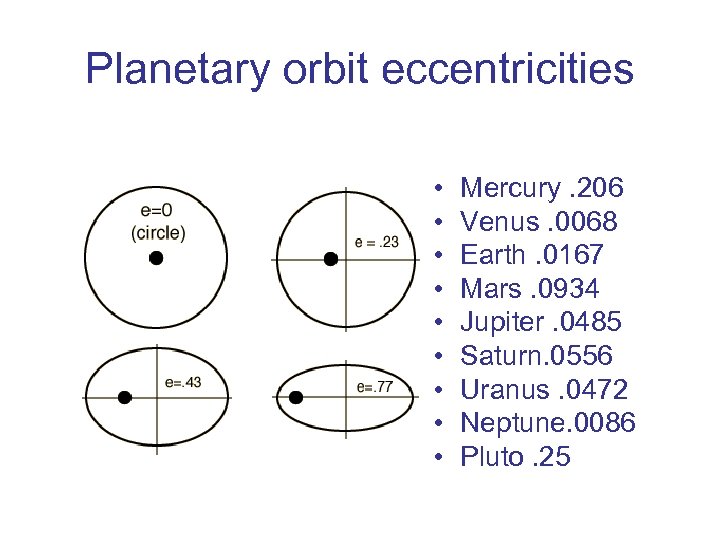Planetary orbit eccentricities • • • Mercury. 206 Venus. 0068 Earth. 0167 Mars. 0934 Jupiter. 0485 Saturn. 0556 Uranus. 0472 Neptune. 0086 Pluto. 25

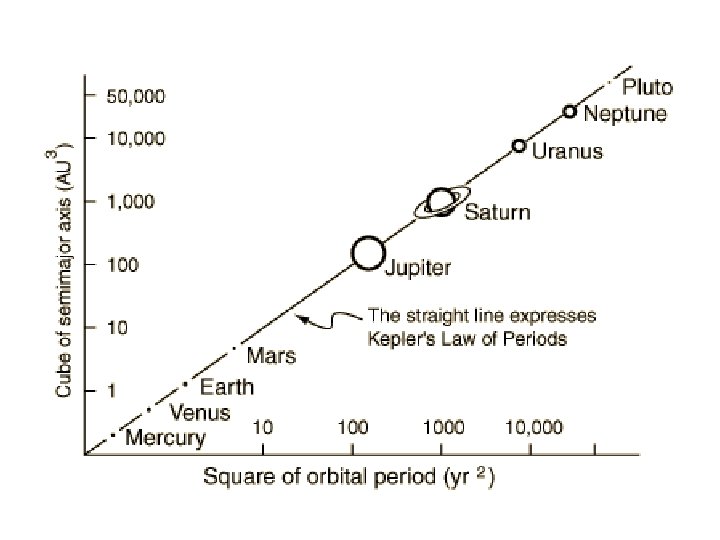
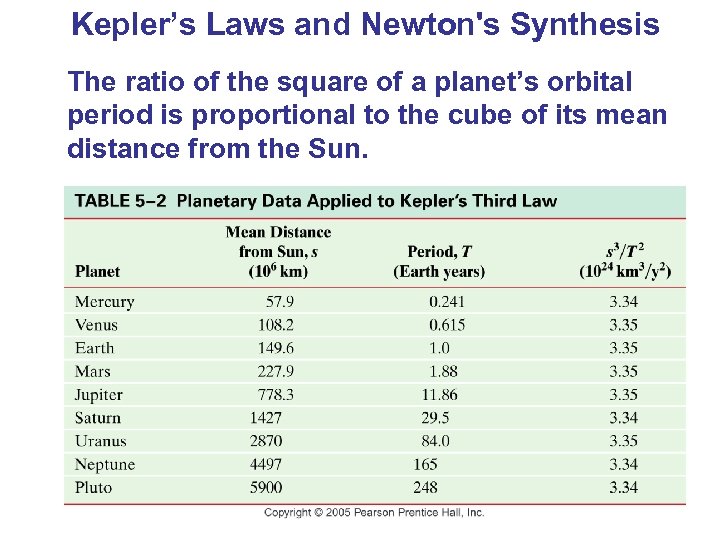Kepler’s Laws and Newton's Synthesis The ratio of the square of a planet’s orbital period is proportional to the cube of its mean distance from the Sun.

Kepler’s Laws and Newton's Synthesis Kepler’s laws can be derived from Newton’s laws. Irregularities in planetary motion led to the discovery of Neptune, and irregularities in stellar motion have led to the discovery of many planets outside our Solar System.

Circular vs. Elliptical Circular speed is constant Elliptical speed varies

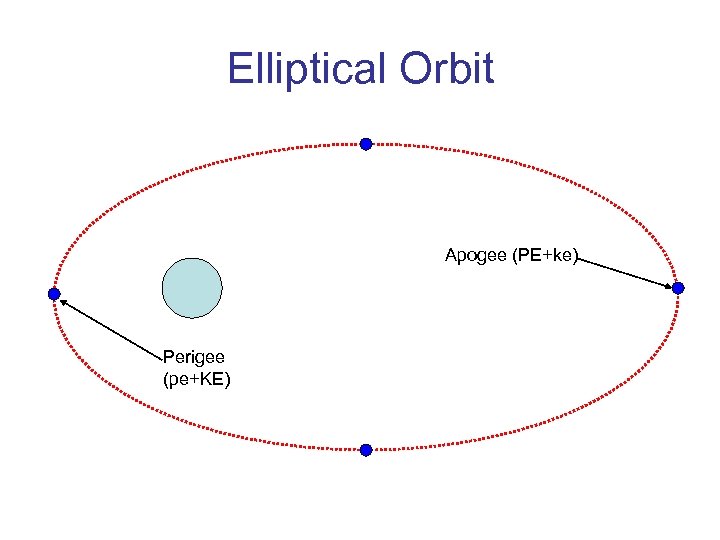Elliptical Orbit Apogee (PE+ke) Perigee (pe+KE)

Elliptical Orbits Where does the satellite have maximum speed? Velocity? Gravitational attraction to Earth? Acceleration? B A C D

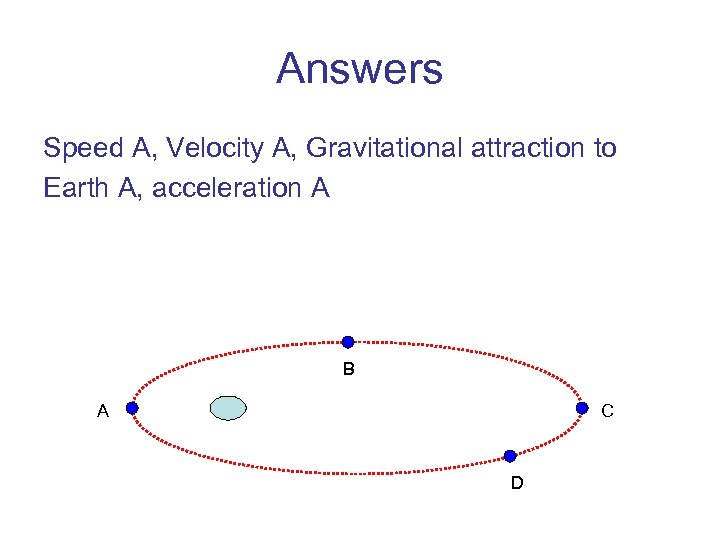Answers Speed A, Velocity A, Gravitational attraction to Earth A, acceleration A B A C D

• What would happen to the Earth if its tangential velocity were reduced to zero?

Solar system Solar System Viewer http: //janus. astro. umd. edu/Solar. Systems/

Weightlessness • Earth-orbiting astronauts are weightless for the same reasons that riders of a freefalling amusement park ride or a freefalling elevator are weightless. They are weightless because there is no external contact force pushing or pulling upon their body.

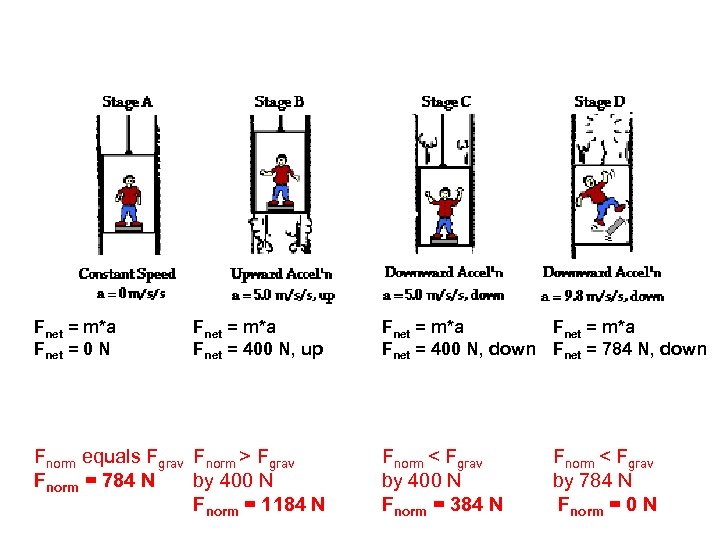Fnet = m*a Fnet = 0 N Fnet = m*a Fnet = 400 N, up Fnorm equals Fgrav Fnorm > Fgrav Fnorm = 784 N by 400 N Fnorm = 1184 N Fnet = m*a Fnet = 400 N, down Fnet = 784 N, down Fnorm < Fgrav by 400 N Fnorm = 384 N Fnorm < Fgrav by 784 N Fnorm = 0 N

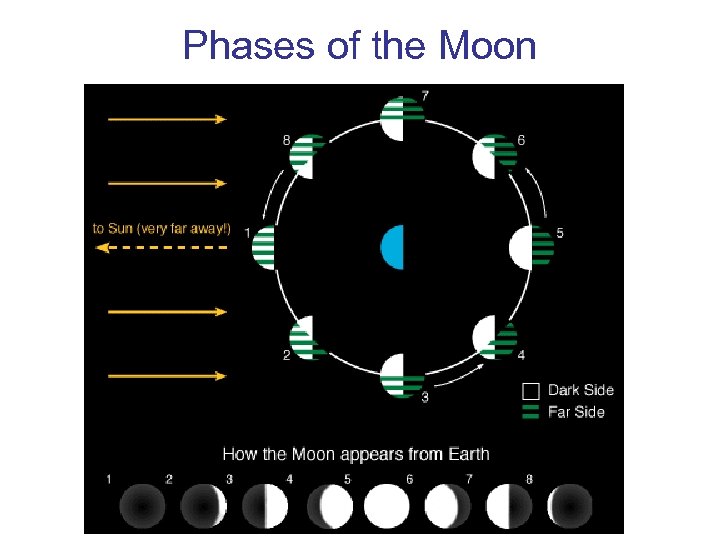Phases of the Moon

Phases of the Moon: [From New Moon to New Moon. . average time for cycle. . 29. 5 days] New Moon. . The Moon's unilluminated side is facing the Earth. The Moon is not visible (except during a solar eclipse). Waxing Crescent. . . The Moon appears to be partly but less than one-half illuminated by direct sunlight. The fraction of the Moon's disk that is illuminated is increasing First Quarter. . . One-half of the Moon appears to be illuminated by direct sunlight. The fraction of the Moon's disk that is illuminated is increasing Waxing Gibbous. . . The Moon appears to be more than one-half but not fully illuminated by direct sunlight. The fraction of the Moon's disk that is illuminated is increasing Full Moon. . . The Moon's illuminated side is facing the Earth. The Moon appears to be completely illuminated by direct sunlight Waning Gibbous. . . The Moon appears to be more than one-half but not fully illuminated by direct sunlight. The fraction of the Moon's disk that is illuminated is decreasing Last Quarter. . . One-half of the Moon appears to be illuminated by direct sunlight. The fraction of the Moon's disk that is illuminated is decreasing Waning Crescent. . . The Moon appears to be partly but less than one-half illuminated by direct sunlight. The fraction of the Moon's disk that is illuminated is decreasing New Moon. . . Phase Cycle starts over. . .

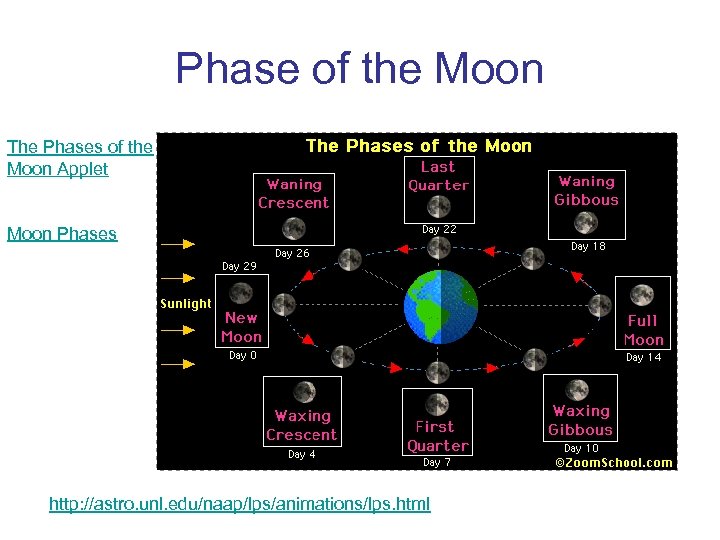Phase of the Moon The Phases of the Moon Applet Moon Phases http: //astro. unl. edu/naap/lps/animations/lps. html

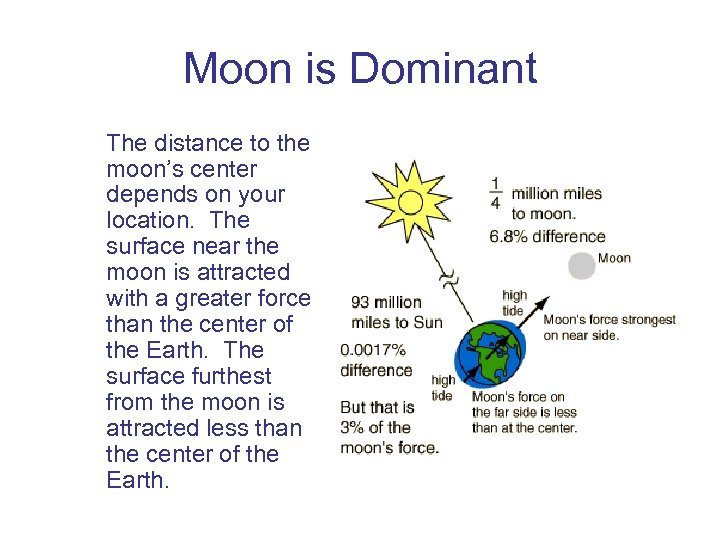Moon is Dominant The distance to the moon’s center depends on your location. The surface near the moon is attracted with a greater force than the center of the Earth. The surface furthest from the moon is attracted less than the center of the Earth.

The Tides • Fctr = GMe. Mm/d 2 • Fsurf = GMe. Mm/(d-re)2 • 1/(d-re)2 = 1/d 2 *(1/(1 -re/d)2) = 1/d 2 *(1+2 re/d) Fsurf = (1+2 re/d)* GMe. Mm/d 2 Fsurf-Fctr = ((1+2 re/d) -1)*GMe. Mm/d 2 = 2 re. GMe. Mm/d 3 The difference varies as the inverse cube of the distance between objects, the sun is much further away, so it has less impact on tides than the moon.

The Tides Tidal Bulge Simulation

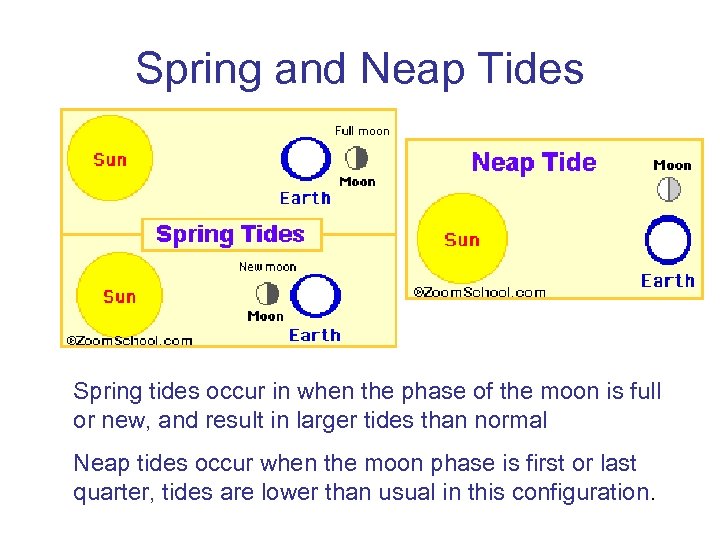Spring and Neap Tides Spring tides occur in when the phase of the moon is full or new, and result in larger tides than normal Neap tides occur when the moon phase is first or last quarter, tides are lower than usual in this configuration.

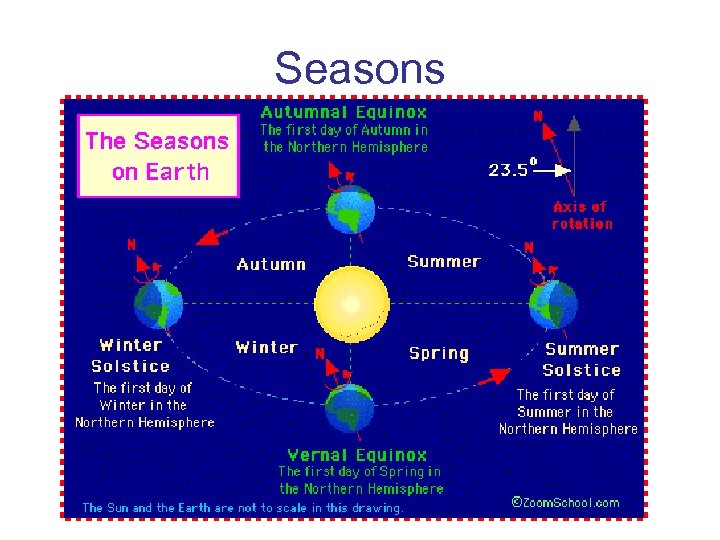Seasons

Seasons http: //www. ioncmaste. ca/homepage/resources/ web_resources/CSA_Astro 9/files/multimedia/un it 3/reasons_seasons. swf Earth-Sun Relations Observing the Sky: Motion of the Earth – Seasons Solar System Viewer

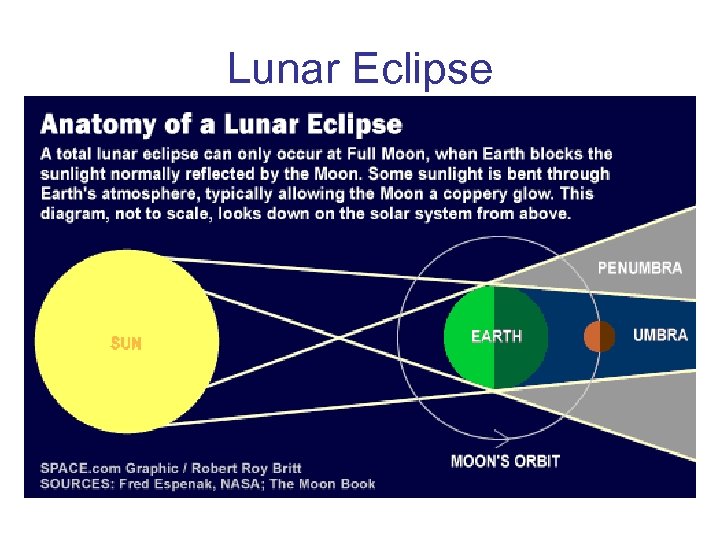Lunar Eclipse

Total Lunar Eclipse

Lunar Eclipse If the Moon’s orbit around the Earth was in the same plane as the Earth’s around the sun we would have a monthly eclipse. Since it is inclined by 5 degrees the moon passes through the ecliptic only twice a month. Lunar Eclipse Animation

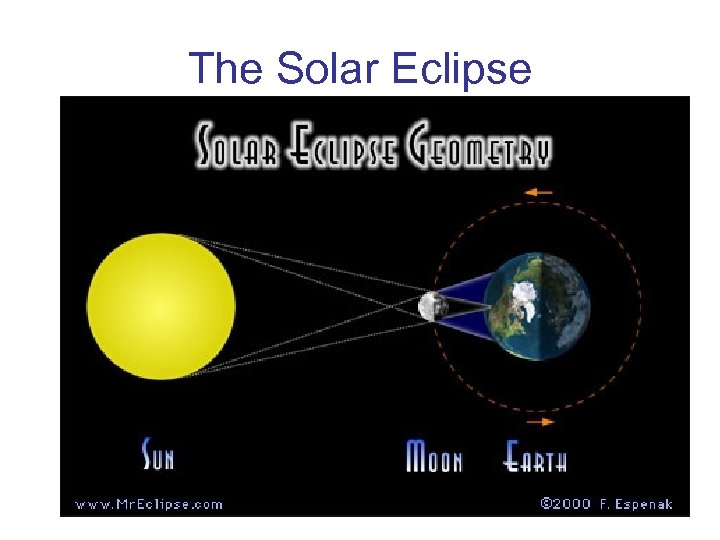The Solar Eclipse

Eclipse http: //www. space. com/media/solar_eclipse_aruba. mov

Solar Eclipse • Eclipse viewed from International space station. Solar Eclipse Animation

Solar Eclipse shot from weather satellite

Eclipse saves Columbus Christopher Columbus and the Lunar Eclipse Columbus Lunar Eclipse http: //courses. ncssm. edu/physvideo/eclipse/l unar_eclipse_11 -8 -03 v 2. mov

Rotation? • The moon keeps one side facing the Earth, does the moon rotate? • Note the “Dark side” or Far side of the moon is always facing away from Earth due to the tidal bulges of the Moon’s surface which are fixed in position.

Summary • Newton’s law of gravitation: force is directly proportional to the mass of the objects and inversely proportional to the square of the distance between the objects center of mass. • Measuring the proportionality constant determined the mass of the Earth • Tides are due to the difference in gravitational force on surface compared to the center of the earth, principle source is moon because the sun is further away