New GCSE Mathematics First teaching Sept 2017 First

New GCSE Mathematics (First teaching Sept 2017) First assessment Summer 2018 (M 1, M 2, M 3, M 4 only) Assessment January 2019 (M 1, M 2, M 3, M 4 only) First full award all units M 1 – M 8 Summer 2019

Legacy GCSE Mathematics Assessment T units January 2018 Assessment T units Summer 2018 Final assessment for T units January 2019

Agenda Revision of GCSE Mathematics Qualifications (for first teaching September 2017) 10. 00 am – 11. 15 am GCSE Mathematics specification and Specimen Assessment Materials 11. 25 am – 12. 15 pm Planning Frameworks – Ruth Crooks 12. 15 pm – 12. 45 pm Lunch 1. 00 pm – 2. 30 pm GCSE Mathematics Problem Solving 2. 30 pm – 3. 00 pm Plenary Q & A

Timeline for new GCSE Maths specification • Legacy specification will be assessed until summer 2018 • There will be a mop up in January 2019 • New GCSE first full award will be in summer 2019

GCSE Mathematics Unique features Employability • New specification • Qualification is linked to and builds on the learning experiences from Key Stage 3 as required for the statutory Northern Ireland Curriculum • Potential pathway into a range of careers in the STEM sector • Programme For Government targets – • Four distinct pathways • Flexibility retained within these pathways • Foundation level – level 1 or level 2 in functional mathematics • New grading A* and C* 20. Increase uptake in economically relevant Science, Technology, Engineering and Mathematics (STEM) places (DEL) 21. Increase the overall proportion of young people who achieve at least 5 GCSEs at A* - C or equivalent including GCSEs in Maths and English by the time they leave school including increase the proportion of young people from disadvantaged backgrounds who achieve at least 5 GCSEs at A* - C or equivalent including GCSEs in Maths and English 42 Improve literacy and numeracy levels among all school leavers, with additional resources targeted at underachieving pupils

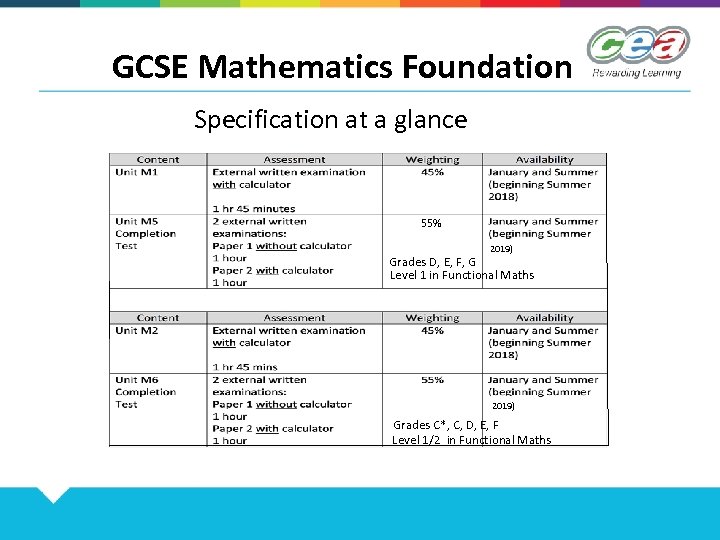GCSE Mathematics Foundation Specification at a glance 55% 2019) Grades D, E, F, G Level 1 in Functional Maths 2019) Grades C*, C, D, E, F Level 1/2 in Functional Maths

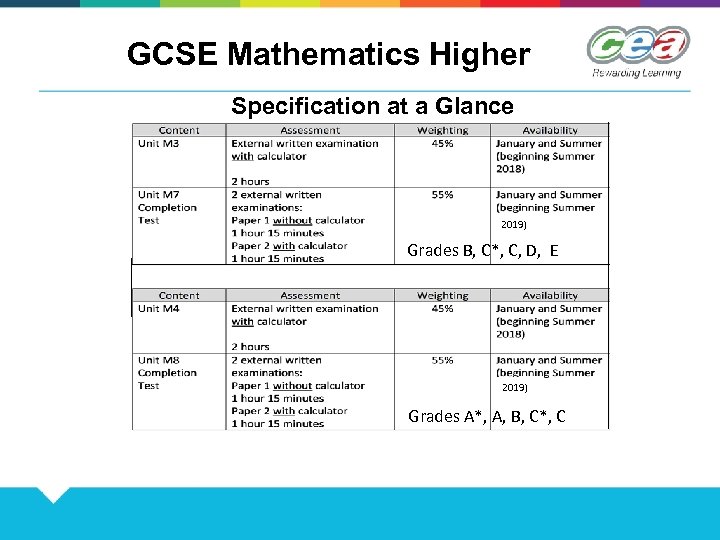GCSE Mathematics Higher Specification at a Glance 2019) Grades B, C*, C, D, E 2019) Grades A*, A, B, C*, C

New GCSE Mathematics • The assessment structure of the qualification has changed. Content has been divided into 8 units – M 1, M 2, M 3, M 4, M 5, M 6, M 7 and M 8. • M 1, M 2, M 5 and M 6 are Foundation Papers. M 3, M 4, M 7 and M 8 are Higher Tier papers. • The completion papers: M 5, M 6, M 7 and M 8 must be taken after M 1, M 2, M 3, and M 4. This is because the completion papers are synoptic. • The completion papers are of greater demand – M 8 is now the most demanding paper because of the volume of content and the additional content which has been added to M 8. Some of this content is new; other content has been moved from T 4.

New GCSE Mathematics • The grading structure has changed. Grades now include a C* and a new A* based on a new formula • A ‘functional elements’ profile will be extracted from the M 1 and M 2 papers. These papers allow for extra reading time. • Level 1 functional mathematics will be awarded for attainment in M 1 and level 2 functional mathematics will be awarded for attainment in M 2 with level 1 if a designated standard is reached. • The new assessment objectives present greater demand challenge. • QWC will be assessed through AO 2. There will be no starred questions on the front cover indicating QWC.

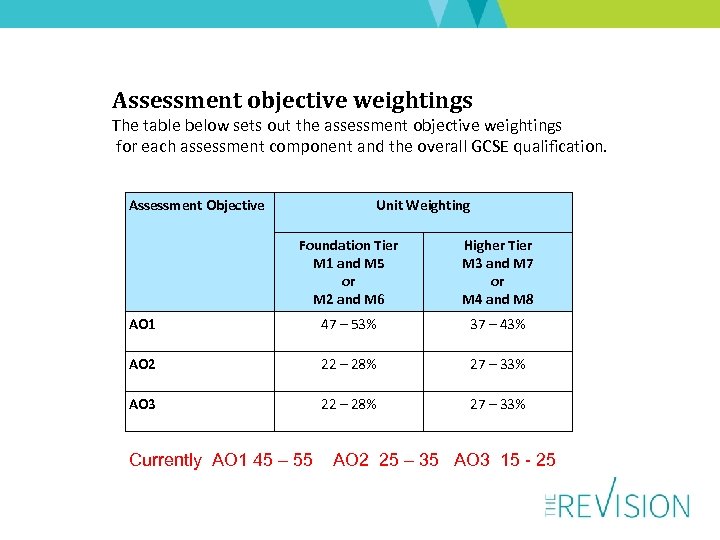Assessment objective weightings The table below sets out the assessment objective weightings for each assessment component and the overall GCSE qualification. Assessment Objective Unit Weighting Foundation Tier M 1 and M 5 or M 2 and M 6 Higher Tier M 3 and M 7 or M 4 and M 8 AO 1 47 – 53% 37 – 43% AO 2 22 – 28% 27 – 33% AO 3 22 – 28% 27 – 33% Currently AO 1 45 – 55 AO 2 25 – 35 AO 3 15 - 25

GCSE Support Materials • Planning Frameworks • Newly added content and content removed • Progression of subject content document e. g M 1 → M 2 → M 3 → M 4 etc • Mapping of content in legacy specification to the new specification (e. g T 4 → M 8) • BBC Bitesize • List of terminology/mathematical language • Guidance on new topics in the specification • Problem solving workshops

Specimen Assessment Materials (SAMS) • Overview of the SAMS • Q & A

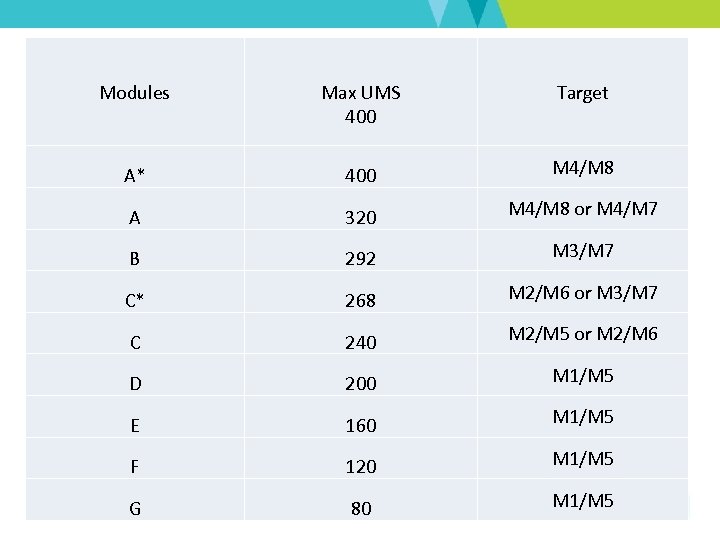Modules Max UMS 400 Target A* 400 M 4/M 8 A 320 M 4/M 8 or M 4/M 7 B 292 M 3/M 7 C* 268 M 2/M 6 or M 3/M 7 C 240 M 2/M 5 or M 2/M 6 D 200 M 1/M 5 E 160 M 1/M 5 F 120 M 1/M 5 G 80 M 1/M 5

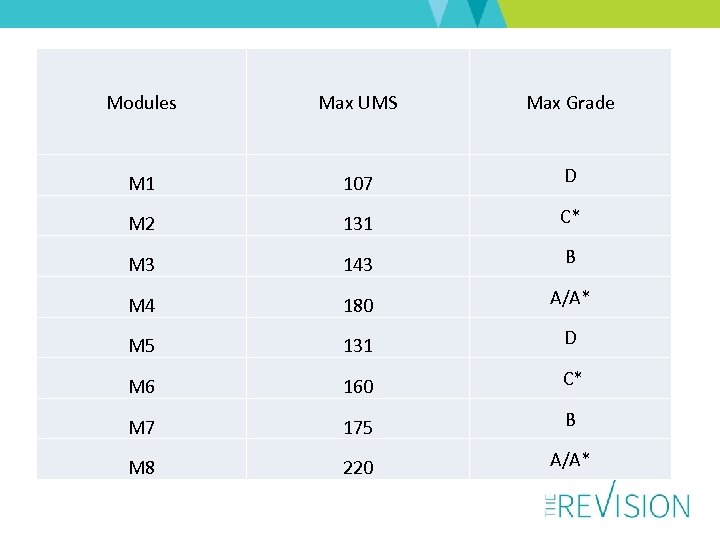Modules Max UMS Max Grade M 1 107 D M 2 131 C* M 3 143 B M 4 180 A/A* M 5 131 D M 6 160 C* M 7 175 B M 8 220 A/A*

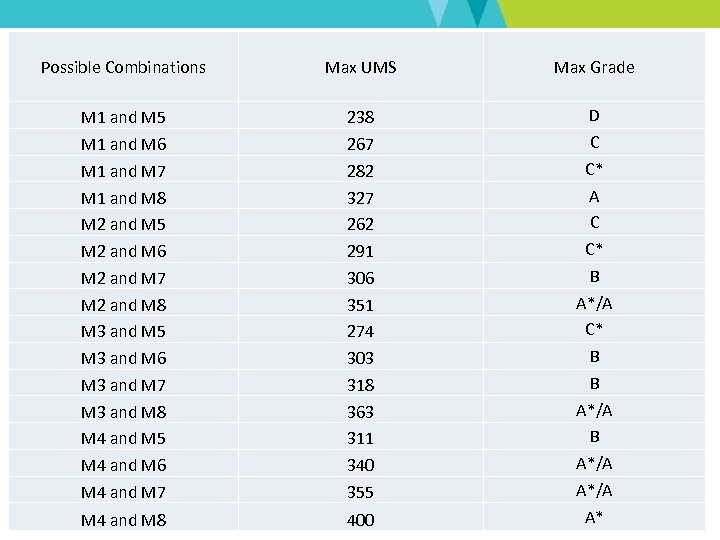Possible Combinations Max UMS Max Grade M 1 and M 5 M 1 and M 6 M 1 and M 7 M 1 and M 8 M 2 and M 5 M 2 and M 6 M 2 and M 7 M 2 and M 8 M 3 and M 5 M 3 and M 6 M 3 and M 7 M 3 and M 8 M 4 and M 5 M 4 and M 6 M 4 and M 7 238 267 282 327 262 291 306 351 274 303 318 363 311 340 355 D C C* A C C* B A*/A C* B B A*/A M 4 and M 8 400 A*

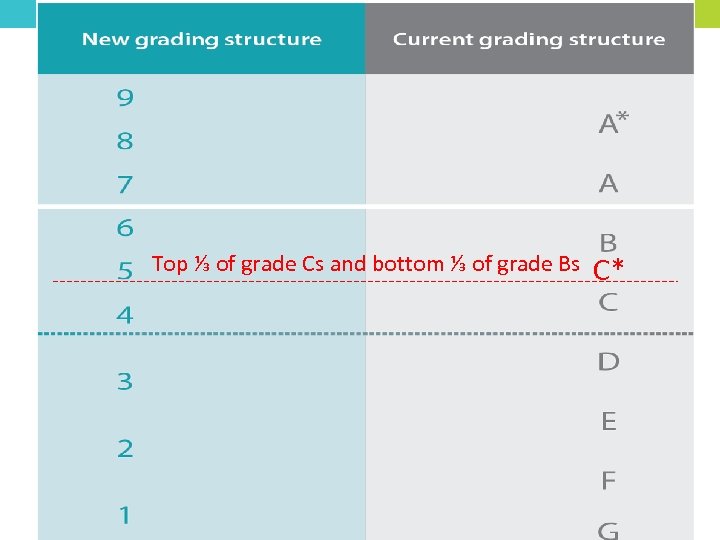Top ⅓ of grade Cs and bottom ⅓ of grade Bs C*

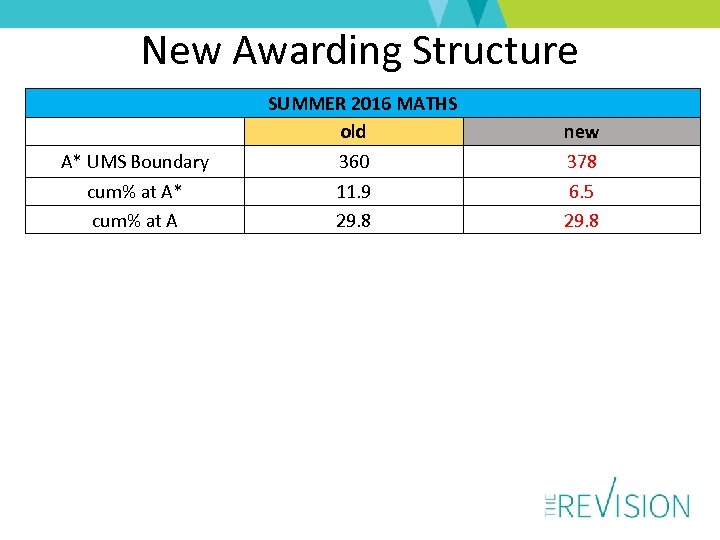New Awarding Structure A* UMS Boundary cum% at A* cum% at A SUMMER 2016 MATHS old new 360 378 11. 9 29. 8 6. 5 29. 8

The Planning Framework • The GCSE Mathematics Planning Framework is a flexible planning tool • Designed to support delivery of the Revised GCSE Mathematics specification

The Planning Framework is not … • Mandatory • Prescriptive • Exhaustive

The Planning Framework is … • Based on the Revised GCSE Mathematics Specification • Draws on the ‘Guidance on Teaching, Learning and Assessment at Key Stage 4’ publication

The Planning framework • Outlines the progression of subject content • Identifies newly added content • Indicates how content in the legacy specification maps to the new specification

The Planning Framework • Provides suggestions for activities: – Knowledge and understanding – Subject specific skills – Cross-Curricular Skills – Thinking Skills and Personal Capabilities

Subject-specific skills • Content and Process skills • Mathematical techniques and Mathematical thinking

Subject-specific skills • Using and applying standard techniques • Reasoning, interpreting and communicating mathematically • Solving problems within mathematics and in other contexts

Using and applying standard techniques • • Accurately recalling facts Accurately recalling terminology Accurately recalling definitions Using notation correctly Interpreting notation correctly Accurately carrying out routine procedures Accurately carrying out set tasks requiring multi-step solutions

Reasoning, interpreting and communicating mathematically • Making deductions to draw conclusions from mathematical information • Making inferences to draw conclusions from mathematical information • Constructing chains of reasoning to achieve a given result • Interpreting information accurately • Communicating information accurately • Presenting arguments • Presenting proofs • Assessing the validity of an argument • Critically evaluating a given way of presenting information

Solving problems within mathematics and in other contexts • Translating problems in mathematical contexts into a process • Translating problems in mathematical contexts into a series of processes • Translating problems in non-mathematical contexts into a mathematical process • Translating problems in non-mathematical contexts into a series of mathematical processes

Solving problems within mathematics and in other contexts • Making connections between different parts of mathematics • Using connections between different parts of mathematics • Interpreting the results in the context of the given problem • Evaluating methods used • Evaluating results obtained • Evaluating solutions to identify how they may have been affected by assumptions made

Becoming functional with Mathematics Subject-specific skills • Content and Process skills • Mathematical techniques and Mathematical thinking

Becoming functional with Mathematics • Use and apply standard mathematical techniques 1 to carry out routine mathematical procedures and set tasks. • Embed the procedures or set tasks into a mathematical problem. • Use and apply mathematical thinking 2 and mathematical techniques to solve a mathematical problem. • Embed the mathematical problem into a real-life problem. • Use and apply mathematical thinking and mathematical techniques to solve a real-life problem in a mathematical way.

Becoming functional with Mathematics • Every Mathematics lesson is an opportunity to develop Mathematical Techniques • Every Mathematics lesson is an opportunity to develop Mathematical Thinking

The Planning Framework • Provides suggestions for a range of teaching and learning activities • Provides flexibility to adapt and develop ideas for your educational setting

PROBLEM SOLVING

Problem-solving skills A problem is something you do not immediately know how to solve. There is a gap between where you are and getting started on a path to a solution. This means that your students require thinking and playingwith-the-problem time. They need to test out ideas, to make conjectures, to go up ‘dead ends’ and adjust their thinking in the light of what they learn from this, discuss ideas with others and be comfortable to take risks. When students are confident to behave in these ways they are then able to step into problems independently rather than immediately turning to us as teachers to ask what to do! As teachers we can support our students to develop the skills they need to tackle problems by the classroom culture we create. It needs to be one where questioning and deep thinking are valued, mistakes are seen as useful, all students contribute and their suggestions are valued, being stuck is seen as honourable and students learn from shared discussion with the teacher, Teaching Assistant(if present) and peers.

New neighbours moved in next door to me. I asked the mother how old were her three sons? She told me that the product of their ages was 36 (all ages are whole numbers) I told her that she hadn’t given me enough information so she told me that the sum of their ages was the same as my house number. I told her that I still couldn’t figure their ages so she told me that her eldest son played the piano. With that, I said “Now, I know their ages! They’re x, y and z

Factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18 & 36 Different products could be 1 X 36 1 X 2 X 18 1 X 3 X 12 1 X 4 X 9 1 X 6 2 X 9 2 X 3 X 6 3 X 4

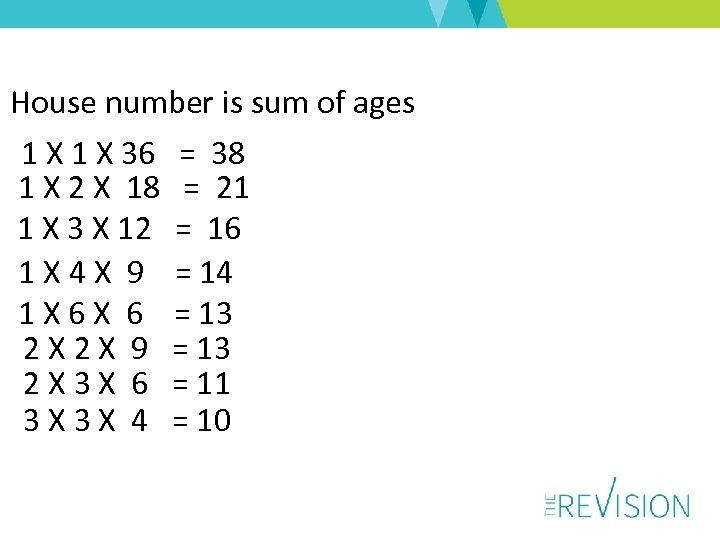House number is sum of ages 1 X 36 = 38 1 X 2 X 18 = 21 1 X 3 X 12 = 16 1 X 4 X 9 = 14 1 X 6 = 13 2 X 9 = 13 2 X 3 X 6 = 11 3 X 4 = 10

I live in number 13 1 X 36 = 38 1 X 2 X 18 = 21 1 X 3 X 12 = 16 1 X 4 X 9 = 14 1 X 6 = 13 2 X 9 = 13 2 X 3 X 6 = 11 3 X 4 = 10

Polya’s First Principle: Understand the problem Polya’s Second Principle: Devise a plan Polya’s Third Principle: Carry out the plan Polya’s Fourth Principle: Look back

PROBLEM SOLVING 1. Gather information 2. Draw sketch, visualisation 3. Write analysis – steps to solve problem, solve a parallel problem, perhaps formulae, own knowledge 4. Solve numerically including units 5. Check – does the answer make sense?

Language ADDITION: sum, plus, and, total, increase, more, raise, both, combined, in all, altogether, additional, extra, appreciate SUBTRACTION: less than, more than, decrease, difference, reduce, change, lost, nearer, farther, left, remain, fell, dropped, discount, depreciate MULTIPLICATION: multiplied, of, product, times, as much, by, twice, three times, tripled, every DIVISION: divide evenly, cut, split, each, every, average, equal pieces, out of, ratio, shared, quotient Toolkit Properties of triangles, quadrilaterals, Pythagoras, area, circle details, prime, even and odd numbers, difference of 2 squares, symmetry ……….

Making an orderly list • How many ways can you arrange the letters A, B and C? ABC (A first) ACB (A first) BAC (B first) BCA (B first) CAB (C first) CBA (C first)

Foundation Paper Summer 2016

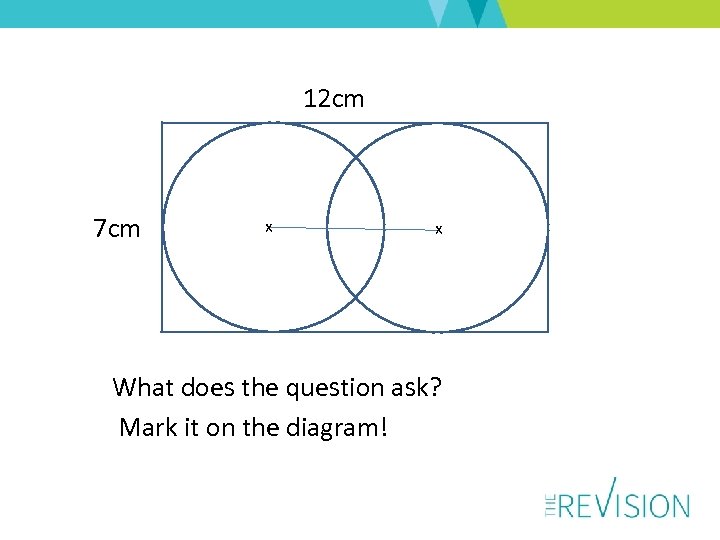12 cm 7 cm x x What does the question ask? Mark it on the diagram!

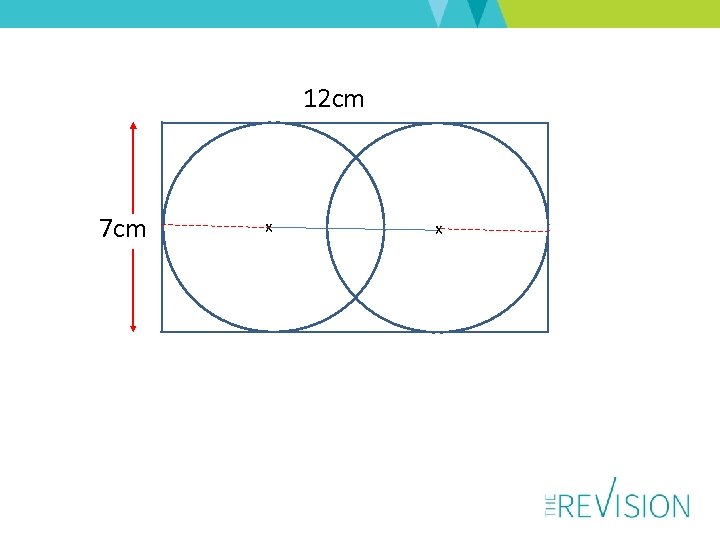12 cm 7 cm x x

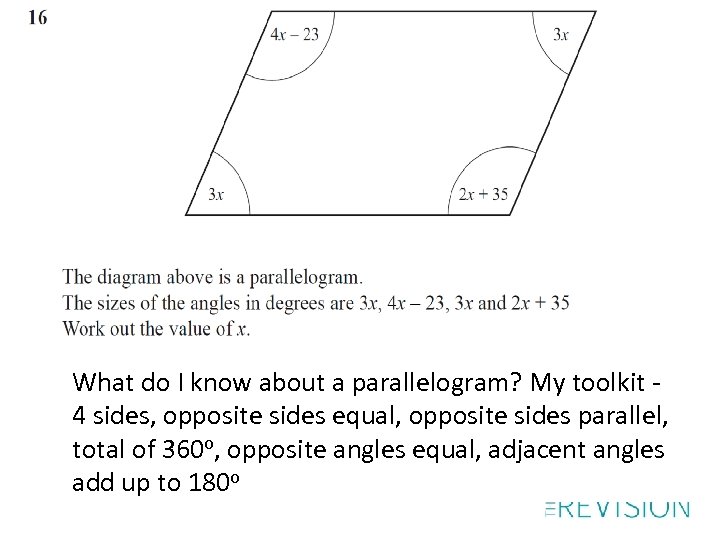What do I know about a parallelogram? My toolkit - 4 sides, opposite sides equal, opposite sides parallel, total of 360 o, opposite angles equal, adjacent angles add up to 180 o

Method 1 Angles add up to 360 o 4 x – 23 + 3 x + 2 x + 35 + 3 x = 360 12 x + 12 = 360 12 x = 348 so x = 29

Method 2 Opposite angles equal 4 x – 23 = 2 x + 35 2 x = 58 x = 29

Method 3 Adjacent angles sum is 180 o 2 x + 35 + 3 x = 180 5 x = 180 - 35 5 x = 145 so x = 29

The Great Race 1. There are nine cars in the race. 2. The white car finished six places behind the blue car. 3. It was raining on the day of the race. 4. The yellow car was in the middle of the order of finishing 5. The green car finished ahead of the black car. 6. All the cars finished the race. 7. The orange car finished between the green and the yellow cars. 8. Only one car finished ahead of the blue car 1. The purple car finished behind the white car. 2. The pink car finished between the yellow and the black cars. 11. The average speed of the cars was 102 mph. 12. The red car finished four cars ahead of the yellow car 13. The green car finished before the yellow car 14. Find the finishing order of the cars.

Over the course of numbering every page in a book, a mechanical stamp printed 2929 individual digits. How many pages does the book have? For a set of five whole numbers, the mean is 4, the mode is 1, and the median is 5. What are the five numbers? A farmer has hens and sheep. There are sixteen heads and thirty-eight feet between these creatures. How many hens does the farmer have?

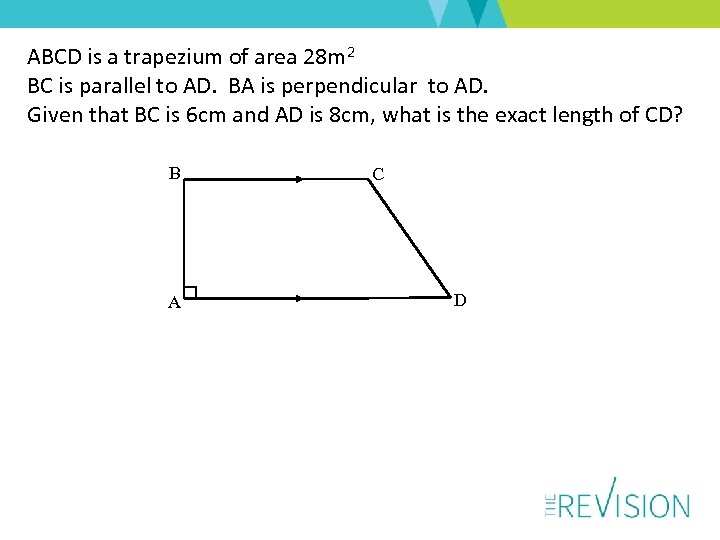ABCD is a trapezium of area 28 m 2 BC is parallel to AD. BA is perpendicular to AD. Given that BC is 6 cm and AD is 8 cm, what is the exact length of CD? B A C D

ABCD is a trapezium of area 28 m 2 BC is parallel to AD. BA is perpendicular to AD. Given that BC is 6 cm and AD is 8 cm, what is the exact length of CD? B 6 cm C 4 cm A 2 cm D Area of trapezium = ½(6 + 8) x AB = 28 AB = 4 Drop perpendicular from C onto AD. CD 2 = 22 + 42 CD 2 = 20 CD = √ 20 = √ 4 x √ 5 = 2√ 5

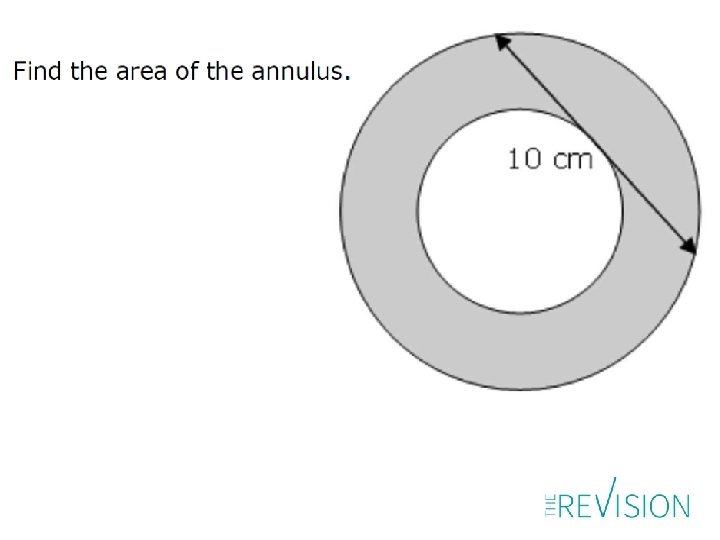
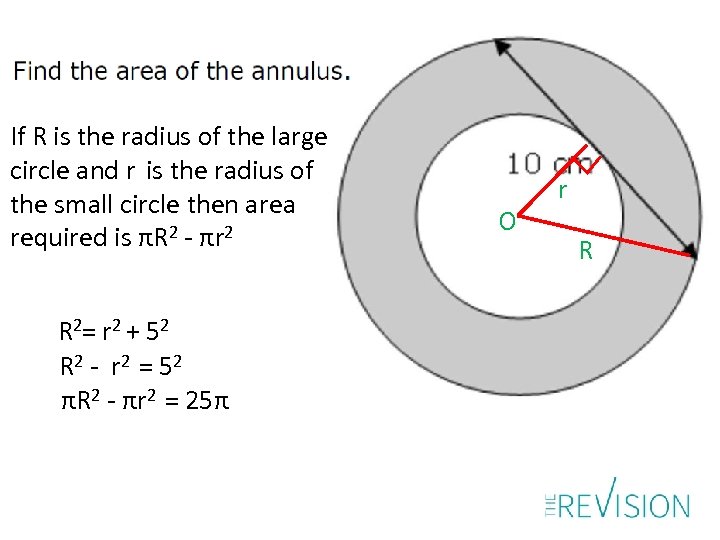If R is the radius of the large circle and r is the radius of the small circle then area required is πR 2 - πr 2 R 2= r 2 + 52 R 2 - r 2 = 52 πR 2 - πr 2 = 25π O r R

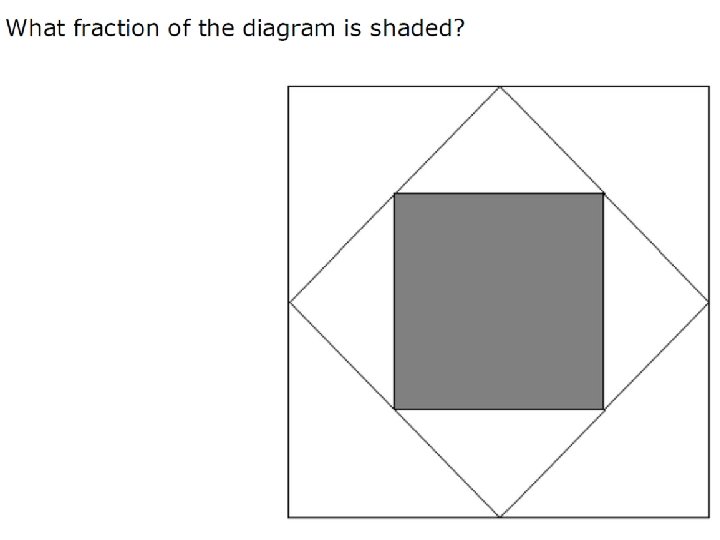
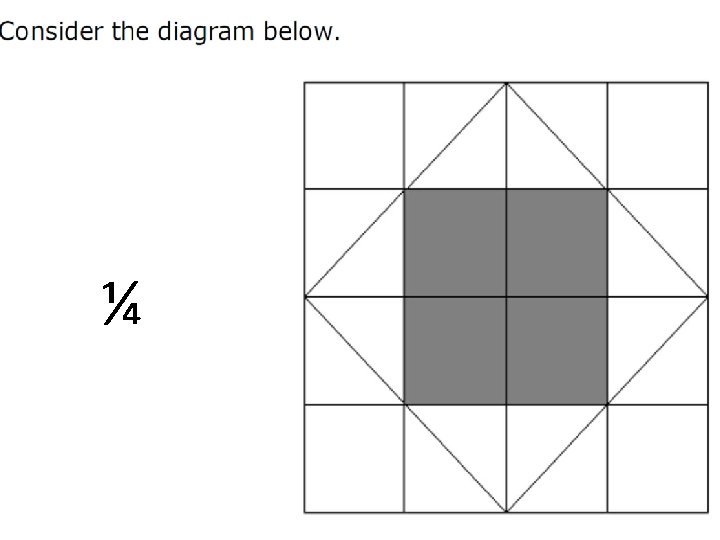¼

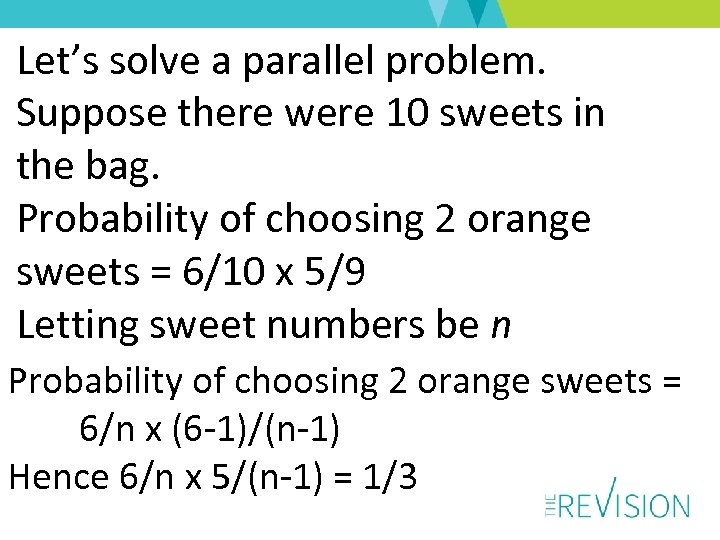Let’s solve a parallel problem. Suppose there were 10 sweets in the bag. Probability of choosing 2 orange sweets = 6/10 x 5/9 Letting sweet numbers be n Probability of choosing 2 orange sweets = 6/n x (6 -1)/(n-1) Hence 6/n x 5/(n-1) = 1/3

At a birthday party, one-half drank only lemonade, one-third drank only cola, fifteen people drank neither, and nobody drinks both. How many people were at the party?

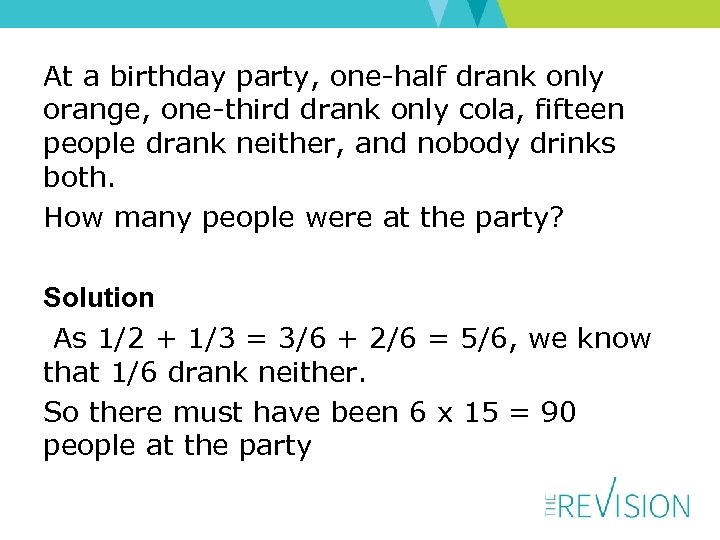At a birthday party, one-half drank only orange, one-third drank only cola, fifteen people drank neither, and nobody drinks both. How many people were at the party? Solution As 1/2 + 1/3 = 3/6 + 2/6 = 5/6, we know that 1/6 drank neither. So there must have been 6 x 15 = 90 people at the party

Mr. and Mrs. Oeuf have two daughters and three sons. At Easter time every member of the family buys one cream egg for each other member. How many cream eggs will be bought in total?

Solution There are seven members of the family and each person must buy six cream eggs. Therefore, total number of cream eggs is 7 x 6 = 42. You could use this idea to work out the following, (i) In a season, 12 schools play home and away matches in a rugby league. How many matches that take place in a season? (ii) In a netball tournament there are 6 teams and each team plays each other team once. How many matches will take place? (iii) In a form class there are 30 girls and 2 are picked at random. How many ways are there of picking them?

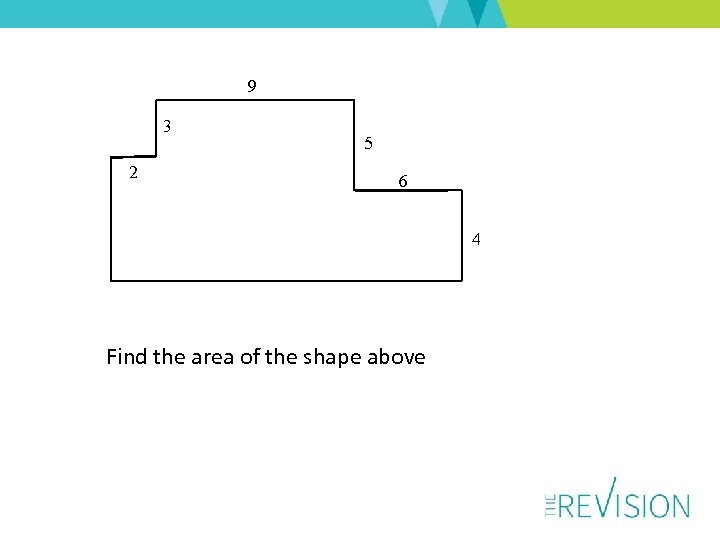9 3 2 5 6 4 Find the area of the shape above

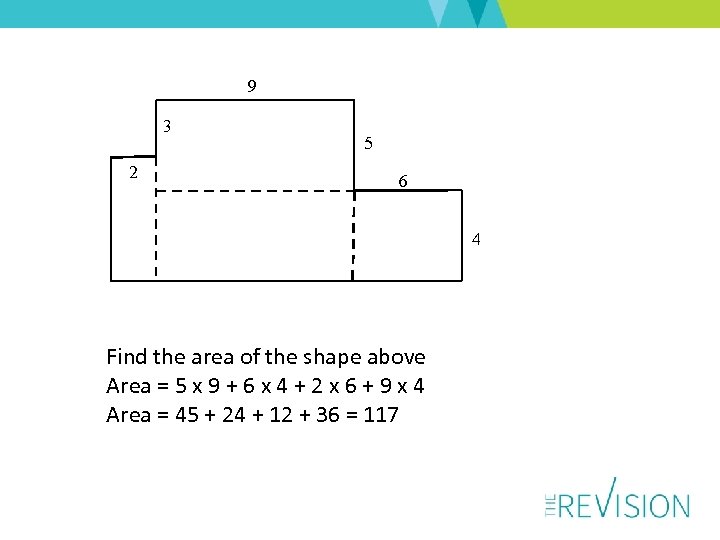9 3 2 5 6 4 Find the area of the shape above Area = 5 x 9 + 6 x 4 + 2 x 6 + 9 x 4 Area = 45 + 24 + 12 + 36 = 117

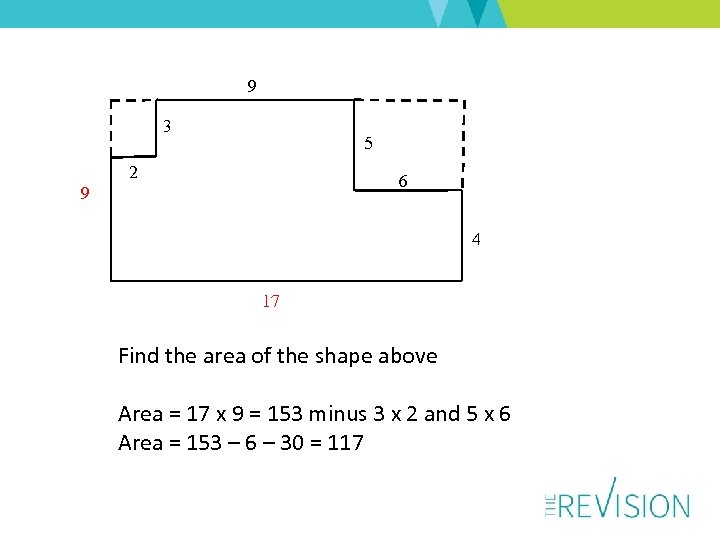9 3 5 2 6 9 4 17 Find the area of the shape above Area = 17 x 9 = 153 minus 3 x 2 and 5 x 6 Area = 153 – 6 – 30 = 117

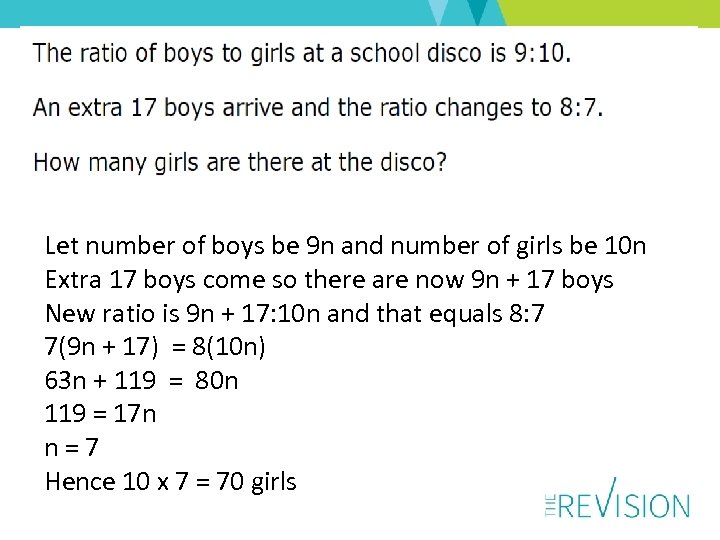Let number of boys be 9 n and number of girls be 10 n Extra 17 boys come so there are now 9 n + 17 boys New ratio is 9 n + 17: 10 n and that equals 8: 7 7(9 n + 17) = 8(10 n) 63 n + 119 = 80 n 119 = 17 n n = 7 Hence 10 x 7 = 70 girls

Divisible by 2 Divisible by 3 Divisible by 4 Prime factors 2 x 2 Divisible by 5 Divisible by 6 Prime factors 2 x 3 Divisible by 7 Divisible by 8 Prime factors 2 x 2 Divisible by 9 Prime factors 3 x 3 Divisible by 10 Prime factors 2 x 5 Number is 2 x 2 x 3 x 5 x 7 = 2520

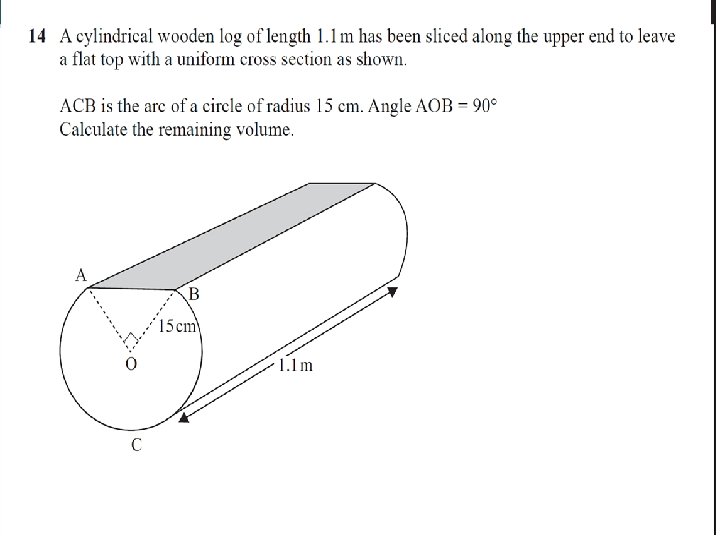
Higher Paper Summer 2014

Right angled triangle Pythagoras Half a rectangle Area = ½bh Even & Odd numbers can be written 2 n and 2 n + 1 O x O = O O x E = E E x E = E

Pythagoras 2 = y 2 + x 2 (y + 1) y 2 + 2 y + 1 = y 2 + x 2 2 y + 1 = x 2 Even & Odd numbers can be written 2 n and 2 n + 1 So 2 y + 1 is an odd number Hence x 2 is an odd number And since O x O = O, x is odd

http: //www. suffolkmaths. co. uk/pages/1 Contextual. Problems. htm http: //www. gottoteach. com/2015/09/non-routine-problem-solving. html Maths challenge. net http: //mathschallenge. net/problems/pdfs/mathschallenge_1_star. pdf http: //www. nicurriculum. org. uk/key_stage_3/areas_of_learning/mathematics/ http: //www. mathster. com/challenge/ http: //www. symbaloo. com/mix/mathsresourcewebsites

http: //www. artofproblemsolving. com/school/about-classroom http: //www. australiancurriculum. edu. au/mathematics/curriculum/f-10? layout=1#level 8 http: //www. australiancurriculum. edu. au/seniorsecondary/mathematics/essentialmathematics/curriculum/seniorsecondary#page=1 http: //www. australiancurriculum. edu. au/mathematics/content-structure https: //www. ncetm. org. uk/resources/45776 http: //www. google. co. uk/url? sa=t&rct=j&q=&esrc=s&source=web&cd=9&ved=0 CF 0 QFj. AI&url= http%3 A%2 F%2 Fwww. asianscholarship. org%2 Fasf%2 Fejourn%2 Farticles%2 FLim%2520 Chap%25 20 Sam 2. doc&ei=HSBNVe. XNAp. CV 7 Abd 44 PACg&usg=AFQj. CNHe. TGCRJgu. HPQYve. POh. FXVT 3 VYkd. A

Why choose CCEA? We support Learners - CCEA puts the learner at the centre of everything we do. We think about what learners need for life and work and then build solutions to meet those needs. We do this for the entire curriculum – from Foundation and Early Years to A level and beyond. We are Local - CCEA is Northern Ireland’s awarding body. We understand local needs and we are focused on providing services and products for learners in Northern Ireland. This also means we’re near you, should you need help or support. We are Listening - CCEA listens to those who use its products and services; this means listening to teachers, employers and learners, and taking action to ensure better outcomes for learners. This approach ensures that we develop relevant, high quality and innovative specifications and support.

Keeping you informed • The Re. Vision microsite – ccea. org. uk/therevision • Essential updates • Specifications & SAMs • Monthly e-Vision newsletter • Subject specific e-alerts Face to face • Social media • Twitter @ccea_info • Facebook ccea. info • Don’t forget to register for your updates on the microsite – ‘keep up to date’ section www. ccea. org. uk/therevision

Contacts: GCSE Mathematics Manager: Joe Mc. Gurk Education Telephone: 028 90 261200 Ext (2106) Email: jmcgurk@ccea. org. uk Subject Support Officer: Nuala Tierney Telephone: 028 90 261200 Ext (2292) Email: ntierney@ccea. org. uk Specification, sample assessment and support materials available on the subject microsite at www. ccea. org. uk