Neutron scattering investigation of TMTTF 2 PF 6 P

Neutron scattering investigation of (TMTTF)2 PF 6 P. Foury-Leylekiana, S. Petitb, B. Hennionb, A. Moradpoura and J. -P. Pougeta a. Laboratoire de Physique des Solides, b. CNRS-UMR 8502, Université Paris-sud, 91405 Orsay, France b. Laboratoire Léon Brillouin, CEA-CNRS, UMR 12, 91191 Gif-sur-Yvette, France ECRYS Cargèse, Corse (F) August 25 -29 2008

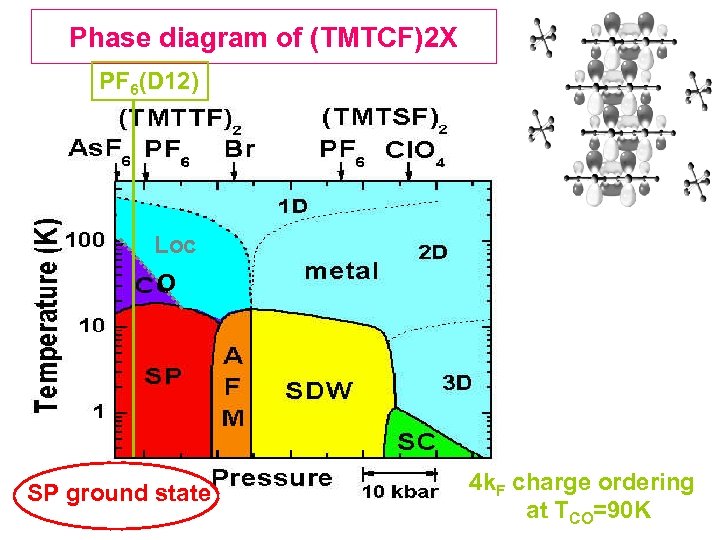Phase diagram of (TMTCF)2 X PF 6(D 12) Loc O SP ground state 4 k. F charge ordering at TCO=90 K

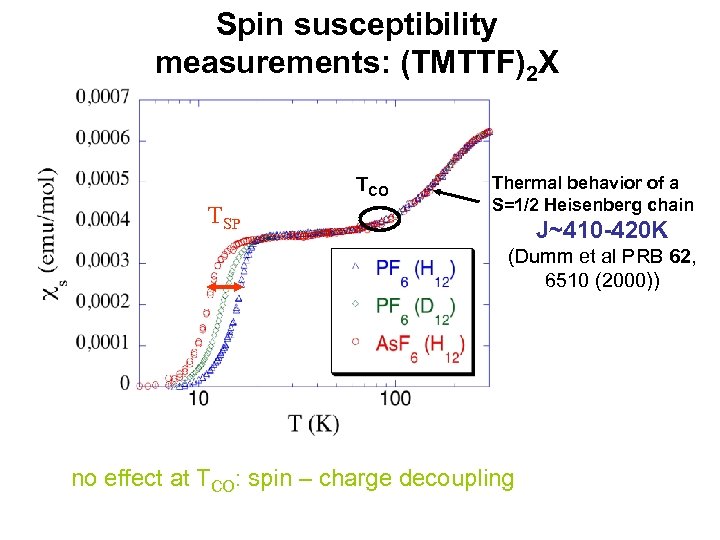Spin susceptibility measurements: (TMTTF)2 X TCO TSP Thermal behavior of a S=1/2 Heisenberg chain J~410 -420 K (Dumm et al PRB 62, 6510 (2000)) no effect at TCO: spin – charge decoupling

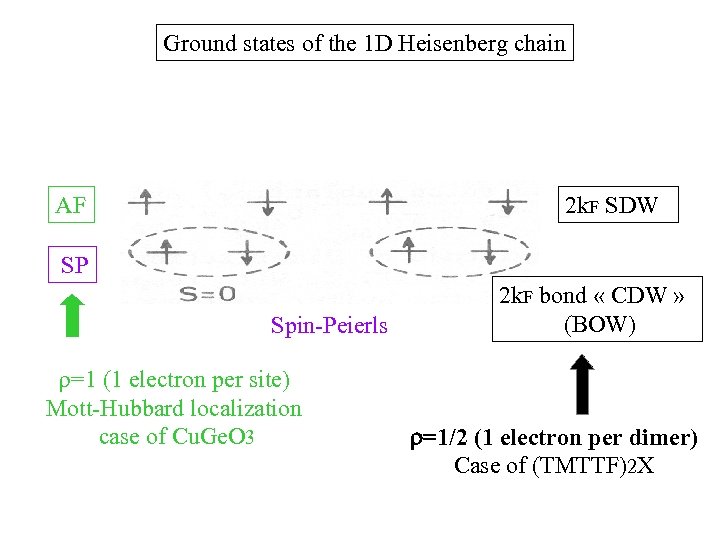Ground states of the 1 D Heisenberg chain AF 2 k. F SDW SP Spin-Peierls r=1 (1 electron per site) Mott-Hubbard localization case of Cu. Ge. O 3 2 k. F bond « CDW » (BOW) r=1/2 (1 electron per dimer) Case of (TMTTF)2 X

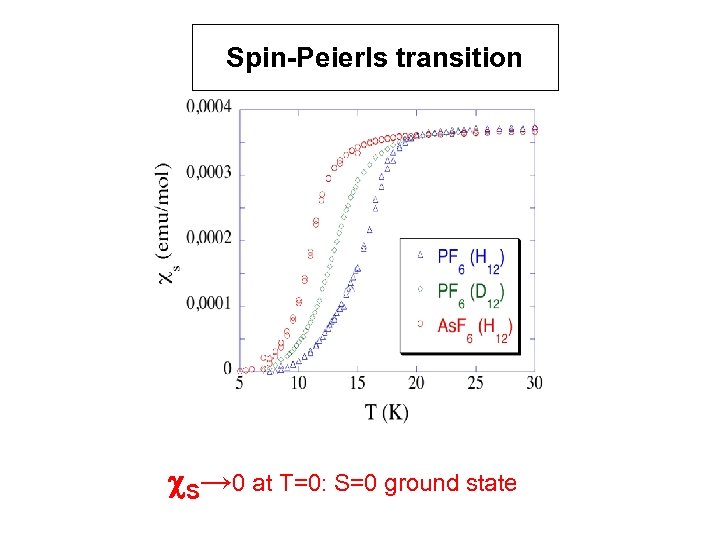Spin-Peierls transition c. S→ 0 at T=0: S=0 ground state

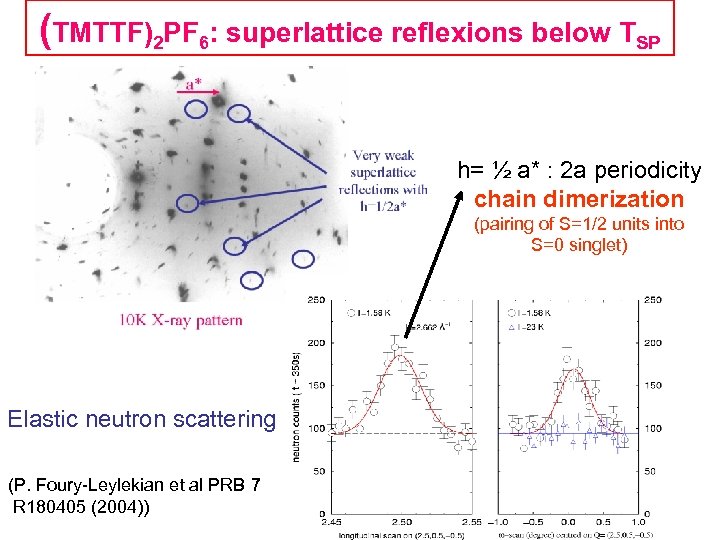(TMTTF)2 PF 6: superlattice reflexions below TSP h= ½ a* : 2 a periodicity chain dimerization (pairing of S=1/2 units into S=0 singlet) Elastic neutron scattering (P. Foury-Leylekian et al PRB 7 R 180405 (2004))

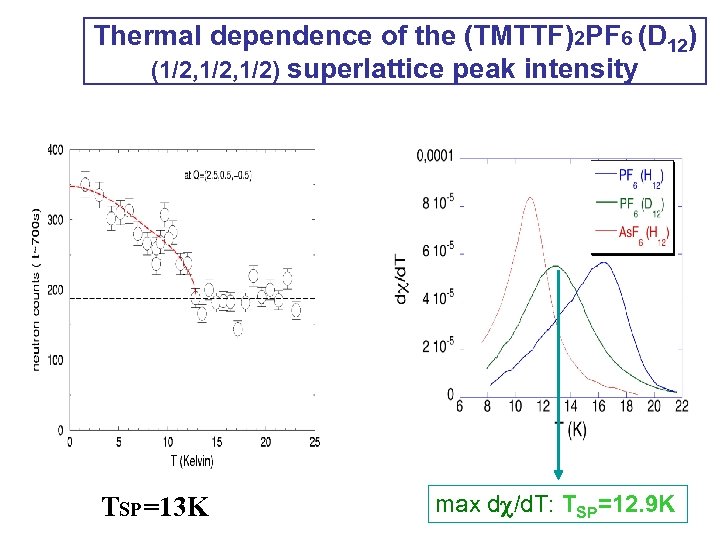Thermal dependence of the (TMTTF)2 PF 6 (D 12) (1/2, 1/2) superlattice peak intensity TSP=13 K max dc/d. T: TSP=12. 9 K

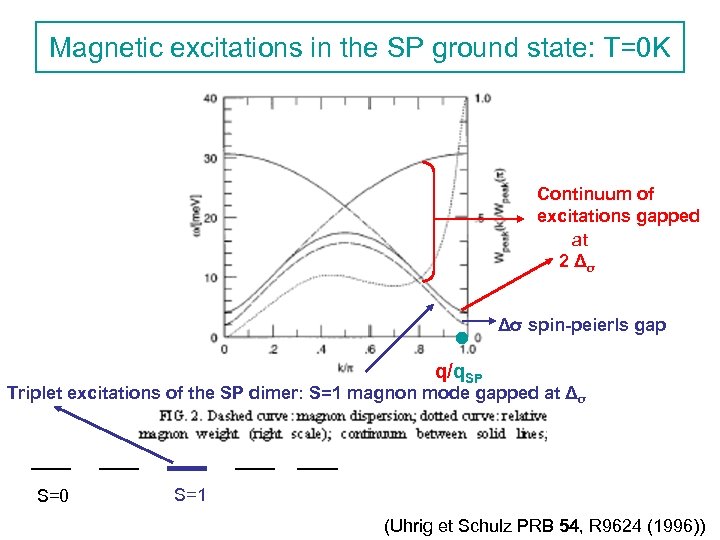Magnetic excitations in the SP ground state: T=0 K Continuum of excitations gapped at 2 Δσ Δσ spin-peierls gap q/q. SP Triplet excitations of the SP dimer: S=1 magnon mode gapped at Δσ S=0 S=1 (Uhrig et Schulz PRB 54, R 9624 (1996))

Magnetic excitations in the SP ground state 1 - magnon mode: propagation of the triplet excitations (S=1) of the SP dimer dispersion: ħωM(q)= E(q) with E(q)=[Δ 2(q)+ε 2(q)]1/2 Δ(q)= Δcos 2πq , ε(q)=Jeff sin 2πq Jeff=J (πJ/2) for the XY(Heisenberg) chain (Bonner & Blote PRB 25, 6959 (1982)) 2 - continuum of double magnon excitations located in between: ħωl(q)= Δ +E(q) and ħωs(q)= 2 E(q/2) (Uhrig & Schulz PRB 54, R 9624 (1996))

Inelastic neutron scattering study • performed with ~1 cm 3 of 98% deuterated (TMTTF)2 PF 6 powder (A. Moradpour LPS) • 2 T triple axis study at Orphée reactor (LLB Saclay)

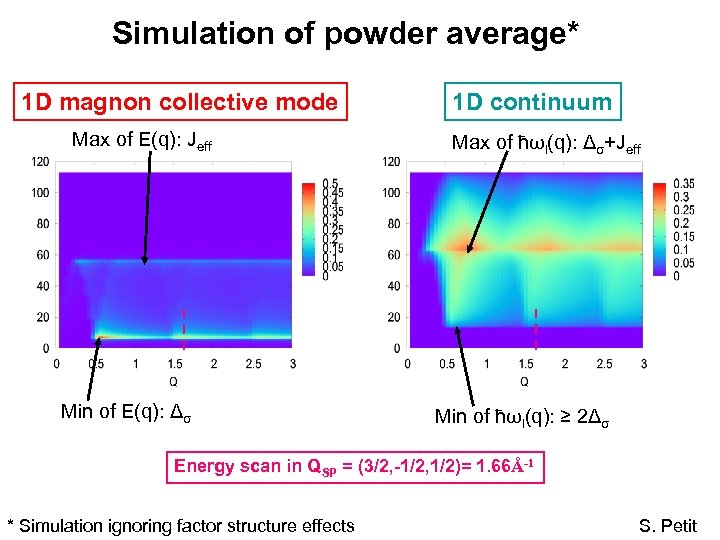Simulation of powder average* 1 D magnon collective mode Max of E(q): Jeff Min of E(q): Δσ 1 D continuum Max of ħωl(q): Δσ+Jeff Min of ħωl(q): ≥ 2Δσ Energy scan in QSP = (3/2, -1/2, 1/2)= 1. 66Å-1 * Simulation ignoring factor structure effects S. Petit

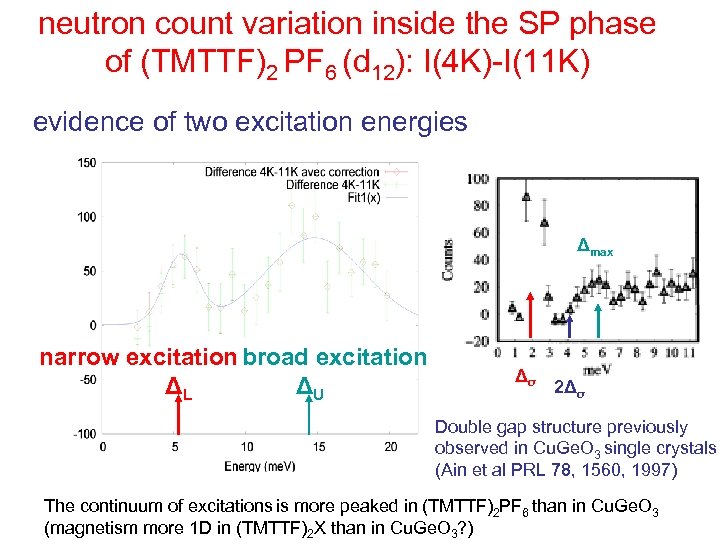neutron count variation inside the SP phase of (TMTTF)2 PF 6 (d 12): I(4 K)-I(11 K) evidence of two excitation energies Δmax narrow excitation broad excitation ΔL ΔU Δσ 2Δσ Double gap structure previously observed in Cu. Ge. O 3 single crystals (Ain et al PRL 78, 1560, 1997) The continuum of excitations is more peaked in (TMTTF)2 PF 6 than in Cu. Ge. O 3 (magnetism more 1 D in (TMTTF)2 X than in Cu. Ge. O 3? )

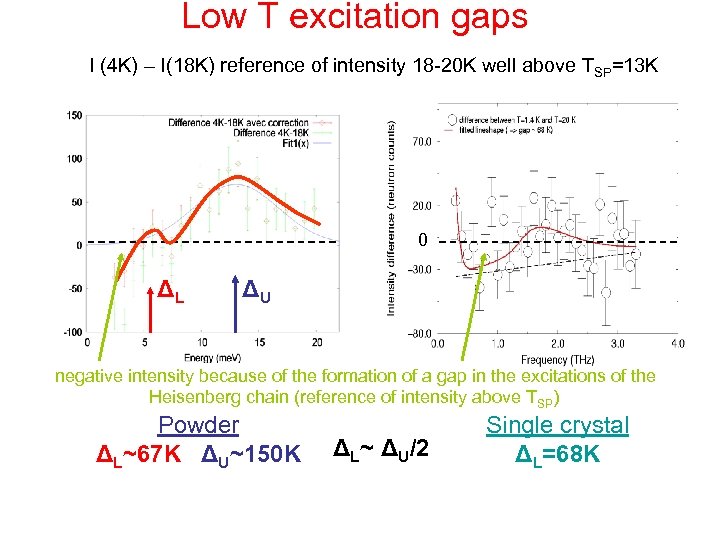Low T excitation gaps I (4 K) – I(18 K) reference of intensity 18 -20 K well above TSP=13 K 0 ΔL ΔU negative intensity because of the formation of a gap in the excitations of the Heisenberg chain (reference of intensity above TSP) Powder ΔL~67 K ΔU~150 K ΔL~ ΔU/2 Single crystal ΔL=68 K

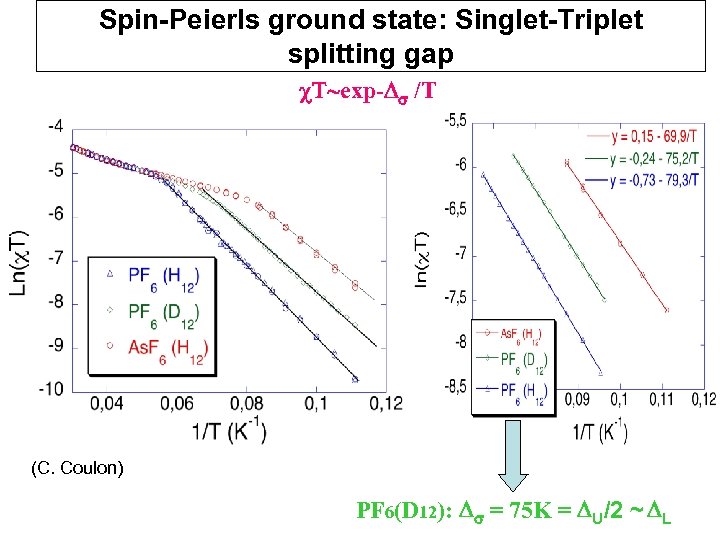Spin-Peierls ground state: Singlet-Triplet splitting gap c. T~exp-Ds /T (C. Coulon) PF 6(D 12): Ds = 75 K = DU/2 ~ DL

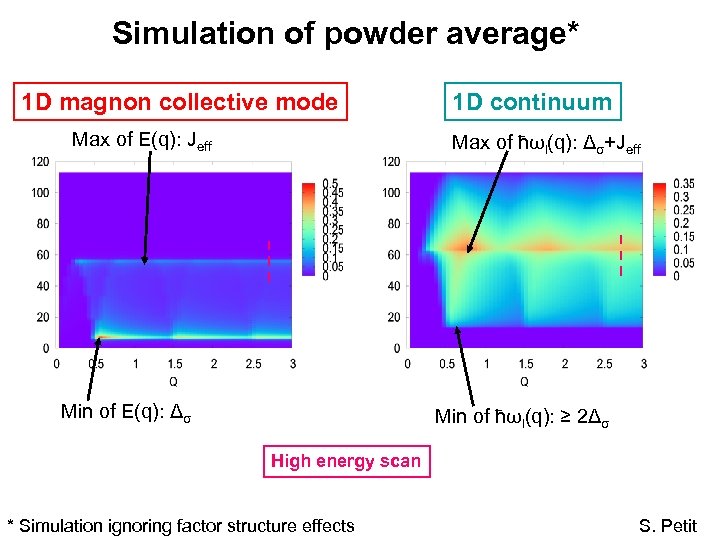Simulation of powder average* 1 D magnon collective mode Max of E(q): Jeff 1 D continuum Max of ħωl(q): Δσ+Jeff Min of E(q): Δσ Min of ħωl(q): ≥ 2Δσ High energy scan * Simulation ignoring factor structure effects S. Petit

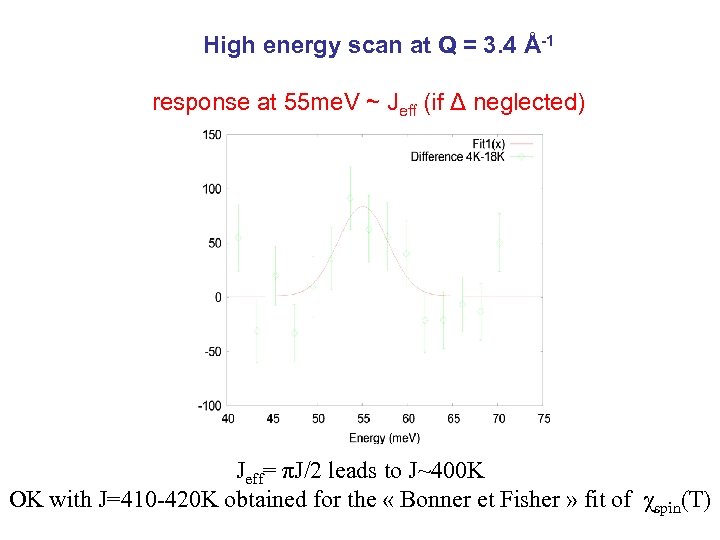High energy scan at Q = 3. 4 Å-1 response at 55 me. V ~ Jeff (if Δ neglected) Jeff= πJ/2 leads to J~400 K OK with J=410 -420 K obtained for the « Bonner et Fisher » fit of χspin(T)

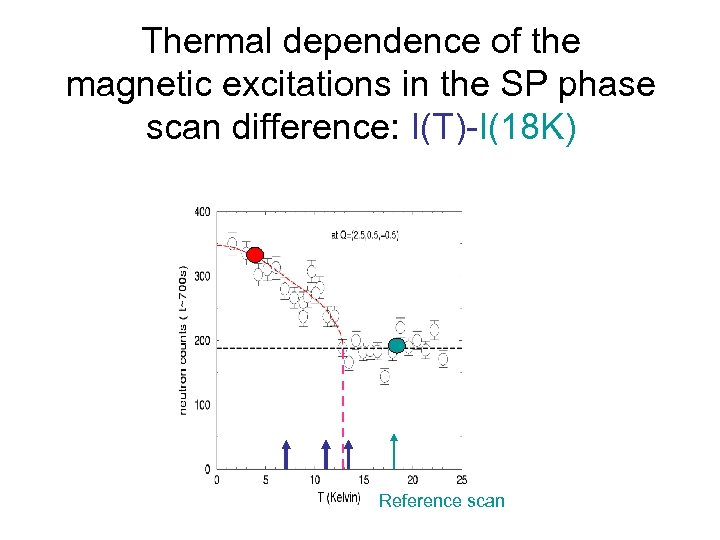Thermal dependence of the magnetic excitations in the SP phase scan difference: I(T)-I(18 K) Reference scan

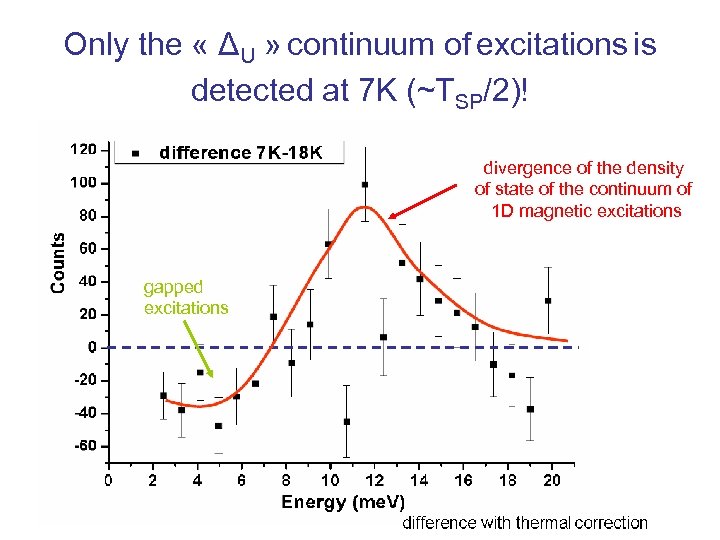Only the « ΔU » continuum of excitations is detected at 7 K (~TSP/2)! divergence of the density of state of the continuum of 1 D magnetic excitations gapped excitations

Reasons for the non–observation of the ΔL magnon peak • Peak merges in the continuum? • Peak intensity vanishes? • Peak broadens? life time effect: efficient decay mode • Possible explanation: magnon mode decays into two bounded spinons on approaching. TSP S=1 X S=1/2 Binding due to unfavorable (out of phase) interchain coupling

Decay of magnon into two bound spinons • Possible near TSP when the cost of interchain coupling is not large • Creation of bound spinons inside the SP phase of (TMTTF)2 PF 6 is possible because the 3 D spin-Peierls distortion (i. e. SP satellite intensity) is very weak (P. Foury-Leylekian et al PRB 70, R 180405 (2004)) • By this scenario one passes continuously (through a 2 nd order transition) when Δ→ 0 from the excitations of the SP chain to those (only a continuum of free spinons) of the Heisenberg chain

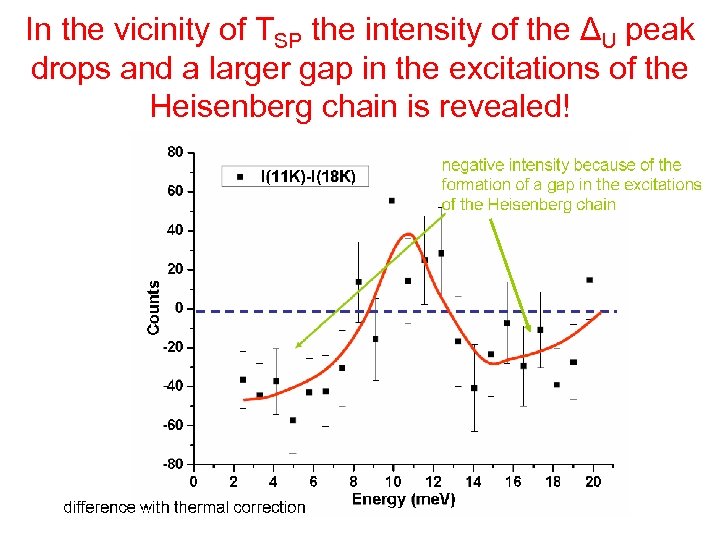In the vicinity of TSP the intensity of the ΔU peak drops and a larger gap in the excitations of the Heisenberg chain is revealed!

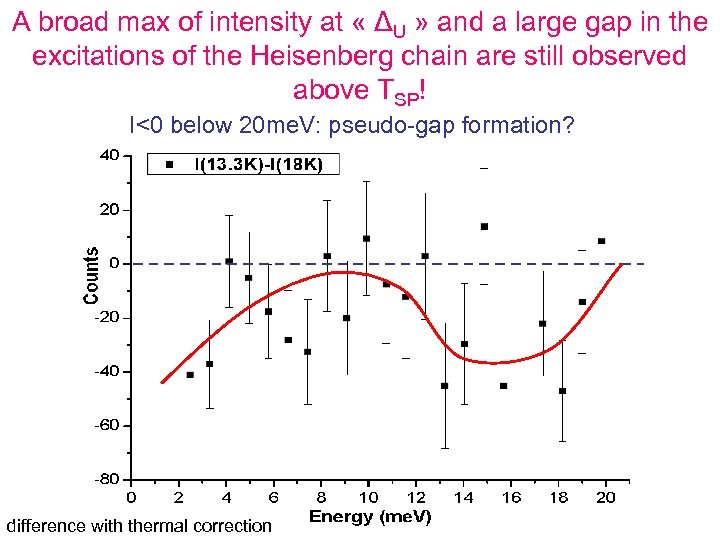A broad max of intensity at « ΔU » and a large gap in the excitations of the Heisenberg chain are still observed above TSP! I<0 below 20 me. V: pseudo-gap formation? difference with thermal correction

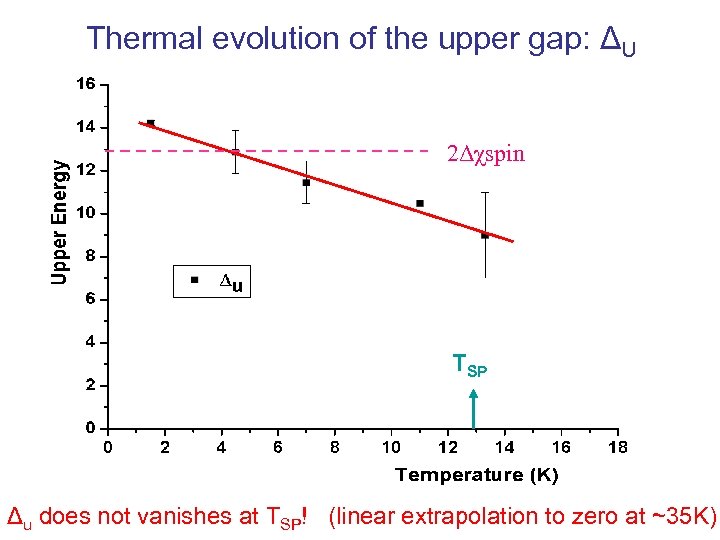Thermal evolution of the upper gap: ΔU 2Δχspin TSP Δu does not vanishes at TSP! (linear extrapolation to zero at ~35 K)

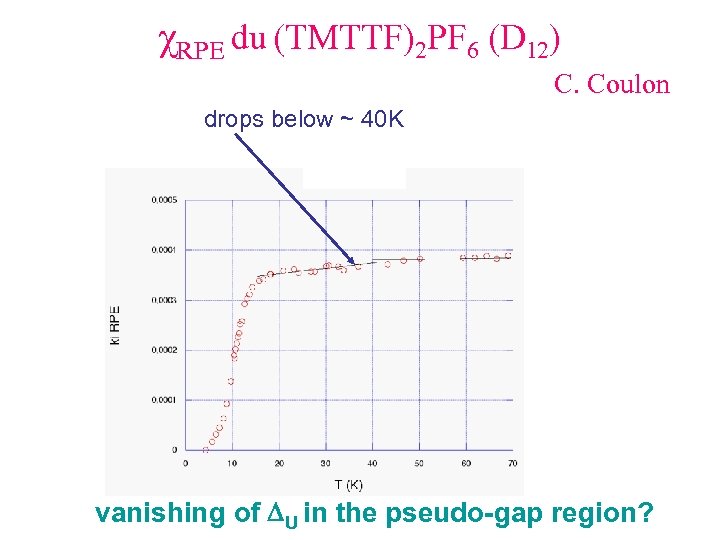χRPE du (TMTTF)2 PF 6 (D 12) C. Coulon drops below ~ 40 K vanishing of DU in the pseudo-gap region?

Pseudo-gap built by SP 1 D structural fluctuations: 1 D X-ray diffuse scattering observed above TSP in (TMTTF)2 PF 6 and As. F 6 1 D structural SP fluctuations above TSP Pouget et al Mol. Cryst. Liq. Cryst. 79, 129 (1982)

mean-field energy scale • 1 D structural fluctuations detected until: ~60 -80 K PF 6 (H 12)- 40 K As. F 6 If one takes TSPMF~60 K for the PF 6 (D 12), the BCS relationship gives: 2Δ 1 DMF~215 K=18. 5 me. V In this energy range inelastic neutron scattering reveals a drop of the magnetic excitation spectrum of the Heisenberg chain negative intensity in the scan difference I(T) - I(18 K)

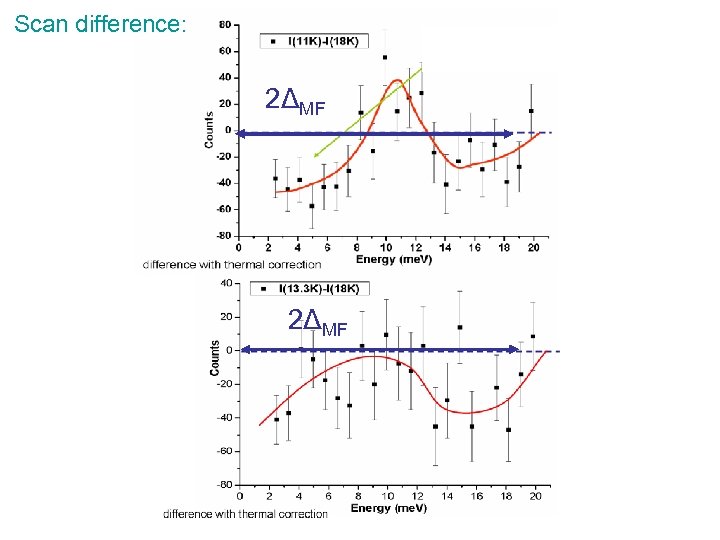Scan difference: 2ΔMF

Summary • This is the first time that magnetic excitations have been measured by neutron scattering in an organic conductor • The SP transition of (TMTTF)2 PF 6 and of Cu. Ge. O 3 differs: in (TMTTF)2 PF 6: - the magnon mode decay inside the SP phase - above TSP: there are pretransitional SP fluctuations and a pseudo gap formation (adiabatic limit) in Cu. Ge. O 3 : - a sharp and intense magnon mode is followed until TSP where Δ vanishes abruptly - no pseudo gap effects are observed above TSP (non adiabatic limit) Crossover of S(q, ω) from the SP ground state (with magnon excitations) to the uniform Heisenberg chain (with spinon excitations) need to be calculated Chain fluctuations needed to be included in the treatment of excitations