Neuro-Fyzzy Methods for Modeling and Identification Presented by

Neuro-Fyzzy Methods for Modeling and Identification Presented by: Ali Maleki

Presentation Agenda Introduction Fuzzy Systems Artificial Neural Networks Neuro-Fuzzy Modeling Simulation Examples

Introduction Control Systems Competion Environment requirements Energy and material costs Demand for robust, fault-tolerant systems Extra needs for Effective process modeling techniques Conventional modeling? lack precise, formal knowledg about the system Strongly nonlinear behavior, High degree of uncertainty, Time varying characteristics

Introduction Solution: Neuro-fuzzy modeling A powerful tool which can facilitate the effective development of models by combining information from different source: Empirical models Heuristics Data Neuro-fuzzy models Describe systems by means of fuzzy if-then rules Represented in a network structure Apply algorithms from the area of Neural Networks

Introduction Neuro-fuzzy modeling - neural networks - fuzzy systems Both are motivated by imitating human reasoning process Relationships: In neural networks : implicitly, coded in the network and its parameters In fuzzy systems: explicitly, in the form of if–then rules Neuro–fuzzy systems combine the semantic transparency of rule-based fuzzy systems with the learning capability of neural networks

Nonlinear system identification NARX (nonlinear autoregressive with exogenous input) model Regressor vector: Dynamic order of the system: Represented by the number of lags nu and ny Task of nonlinear system identification: Infer unknown function f from available data sequences

Nonlinear system identification Multivariable systems: Nonlinear state-space discription Task of nonlinear system identification: Infer unknown functions g and h from available data sequences Neural Networks Neuro-fuzzy systems Splines Interpolated look-up tables Accurate Predictor Accurate predictor + model that can be used to learn something about system + Analyse system properties

Fuzzy Models

Fuzzy Models Definition: A mathematical model which in some way uses fuzzy sets In system identification: rule-based fuzzy models Example: IF heating is high THEN temperature increase is fast Linguistic terms To make such a model operational: Linguistic terms must be defined more precisely using fuzzy sets Fuzzy sets defined through their membership functions

Fuzzy Models Types of fuzzy models: (depending on the structure of if-then rules) Mamdani Model IF D 1 is low and D 2 is high THEN D is medium Takagi-Sugeno Model IF D 1 is low and D 2 is high THEN D=k (zero- IF D 1 is low and D 2 is high THEN D=0. 7 D 1+0. 2 D 2+0. 1 (first-order)

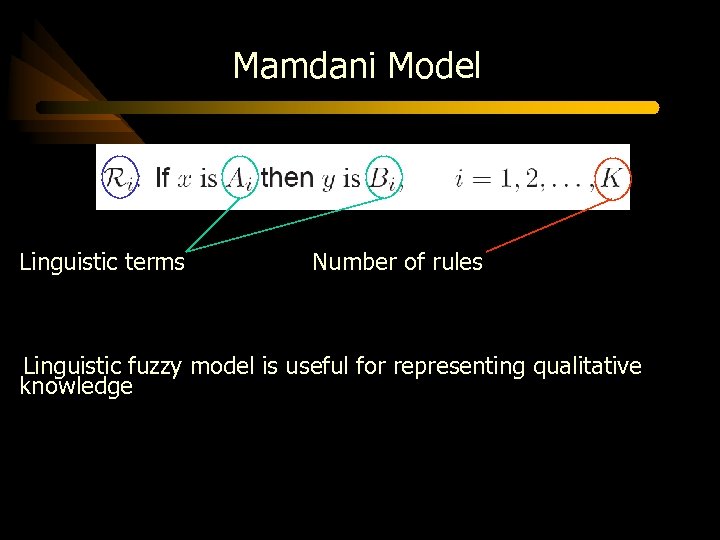
Mamdani Model Linguistic terms Number of rules Linguistic fuzzy model is useful for representing qualitative knowledge

Example – Mamdani Model Oxygen flow rate Gas burner Heating power Linguistic terms is defined by membership function

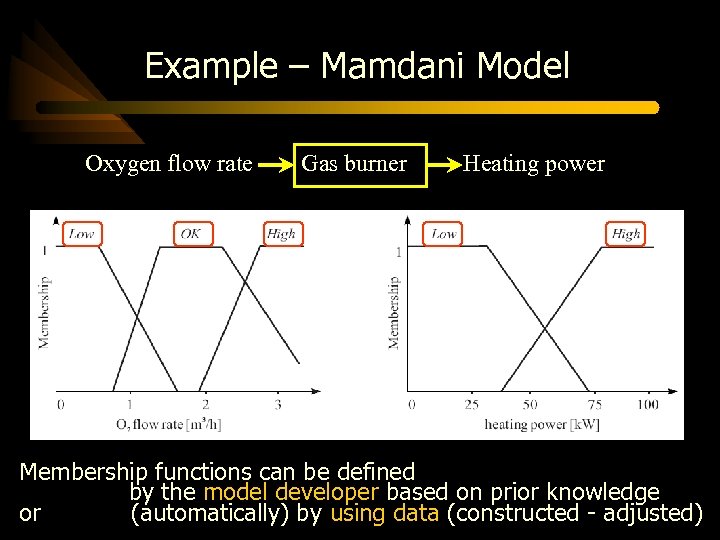
Example – Mamdani Model Oxygen flow rate Gas burner Heating power Membership functions can be defined by the model developer based on prior knowledge or (automatically) by using data (constructed - adjusted)

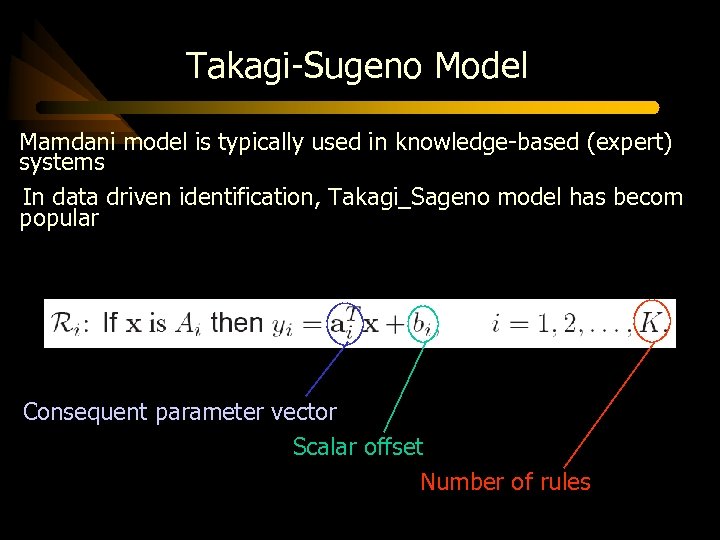
Takagi-Sugeno Model Mamdani model is typically used in knowledge-based (expert) systems In data driven identification, Takagi_Sageno model has becom popular Consequent parameter vector Scalar offset Number of rules

Takagi-Sugeno Model The output y is computed by taking the weighted average of the individual rules contribution: Degree of fulfilment of the ith rule In a special case:

Takagi-Sugeno Model (zero-order) Rules: Input-output equation: This model is a special case of the Mamdani system, in which Consequent fuzzy sets degenerate to singletons (real numbers)

Takagi-Sugeno Model usually, antecedent fuzzy sets are usually defined to describe distinct, partly overlapping regions in the input space Then, The parameters ai are approximate local linear models of the considered nonlinear system TS model: Piece-wise linear approximation of a nonlinear function

Example: Takagi-Sugeno Model static characteristic of an actuator with dead zone and a non-symmetrical response for positive and negative inputs

Fuzzy Logic Operators In fuzzy systems with multiple inputs, the antecedent proposition is usually represented as a combination of terms, by using logic operators ‘and’ (conjunction) ‘or’ (disjunction) and ‘not’ (complement) In fuzzy set theory, several families of operators have been introduced for these logical connectives

Example: Fuzzy Logic Operators conjunctive form of the antecedent degree of fulfillment: minimum conjunction operator product conjunction operator

Dynamic Fuzzy Models TS NARX model Regressor vector

Dynamic Fuzzy Models TS state-space model Advantages of the state-space modeling approach: • structure of the model can easily be related to the physical structure of the real system (model parameters are physically relevant) • This is not necessarily the case with input-output models. • Dimension of the regression problem in state-space modeling is often smaller than with input–output models

Artificial Neural Networks ANNs: • Inspired by the functionality of biological neural networks • Can generalizing from a limited amount of training data • black-box models of nonlinear, multivariable static and dynamic systems • can be trained by using input–output data ANNs • • • consist of: Neurons Interconnection among them Weights assigned to these interconnections

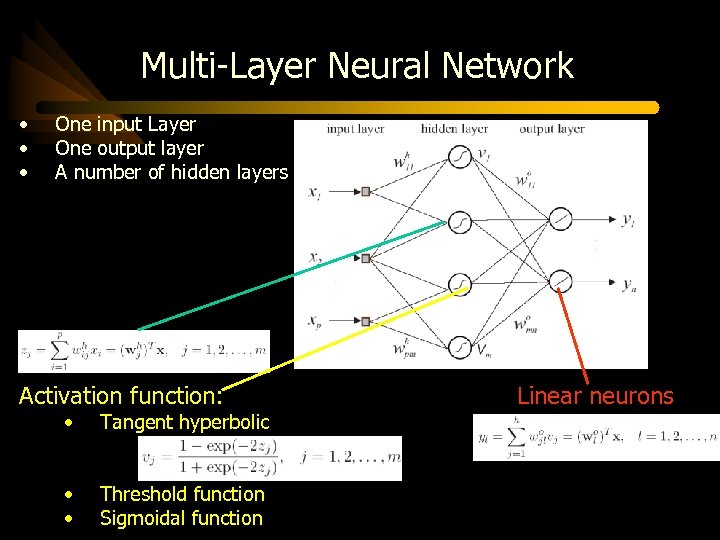
Multi-Layer Neural Network • • • One input Layer One output layer A number of hidden layers Activation function: • Tangent hyperbolic • • Threshold function Sigmoidal function Linear neurons

Multi-Layer Neural Network - Training definition: • adaptation of weights in a multi-layer network such that the error between the desired output and the network output is minimized Training steps: • Feedforward computation • Weight adaptation Gradient-descent optimization Error backpropagation

Multi-Layer Neural Network - Structure A network with one hidden layer is sufficient for most approximation tasks More layers: • Can give a better fit • But the training takes longer number of neurons in the hidden layer: • Too few neurons give a poor fit • Too many neurons result in overtraining of the net (poor generalization to unseen data)

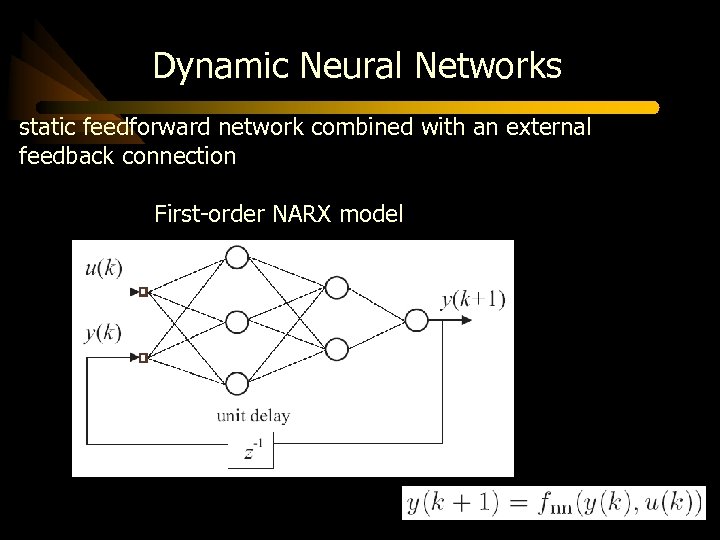
Dynamic Neural Networks static feedforward network combined with an external feedback connection First-order NARX model

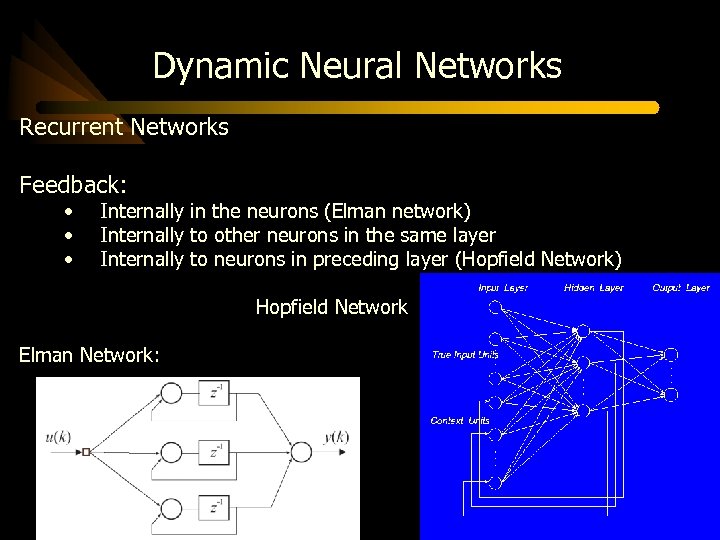
Dynamic Neural Networks Recurrent Networks Feedback: • • • Internally in the neurons (Elman network) Internally to other neurons in the same layer Internally to neurons in preceding layer (Hopfield Network) Hopfield Network Elman Network:

Error Backpropagation Input: Desired output: Error: Cost function: Adjusting the weights: minimization of the cost function

Error Backpropagation network’s output y is nonlinear in the weights Therefore, The training of a MNN is thus a nonlinear optimization problem Methods: • Error backpropagation (first-order gradient) • Newton, Levenberg-Marquardt methods (second-order gradient) • Genetic algorithms and many others techniques

Error Backpropagation First-order gradient Update rule: Weight vector in iteration n Learning rate Jacobian of the network nonlinear optimization problem is thus solved by using the first term of its Taylor series expansion

Error Backpropagation Second-order gradient: Second-order gradient method make use of the second term Hessian Update rule:

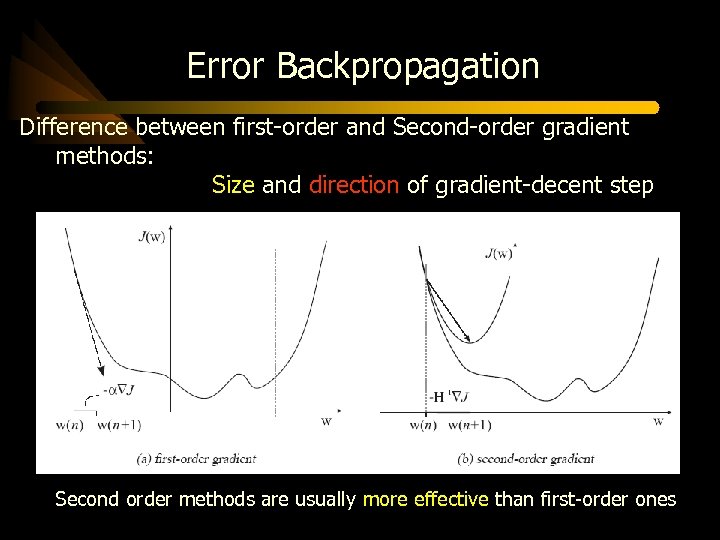
Error Backpropagation Difference between first-order and Second-order gradient methods: Size and direction of gradient-decent step Second order methods are usually more effective than first-order ones

Error Backpropagation For output layer Update law for output weights: For hidden layer Update law for hidden layer weights: Backpropagation error

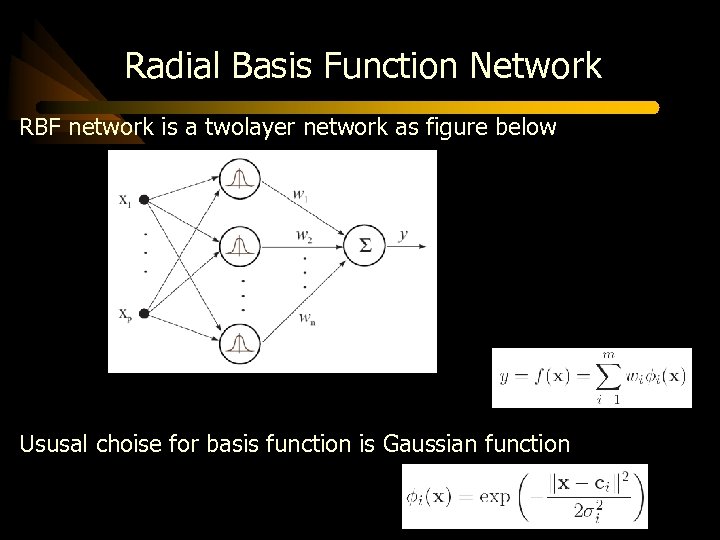
Radial Basis Function Network RBF network is a twolayer network as figure below Ususal choise for basis function is Gaussian function

Radial Basis Function Network Adjustable weights are only present in the output layer Free parameters of RBF nets are • Output weights • Parameters of the basis functions (centers and radii) Output is linear in the weights, and these weights can be estimated by least-squares methods adaptation of the RBF parameters (center and radial) is a nonlinear optimization problem that can be solved by the gradient-descent techniques

Neuro-Fuzzy Modeling Fuzzy system as a layered structure (network), similar to ANNs of the RBF type gradientdescent training algorithms for parameter optimization This approach is usually referred to as Neuro-Fuzzy Modeling • • Zero-order TS fuzzy model First-order TS fuzzy model

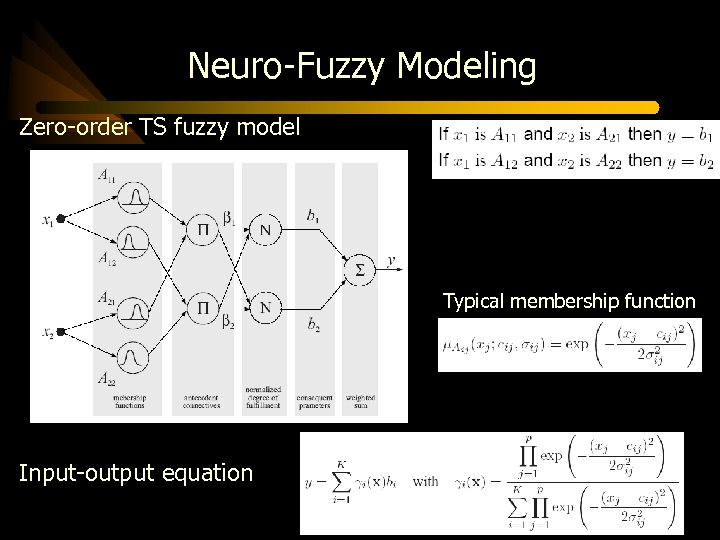
Neuro-Fuzzy Modeling Zero-order TS fuzzy model Typical membership function Input-output equation

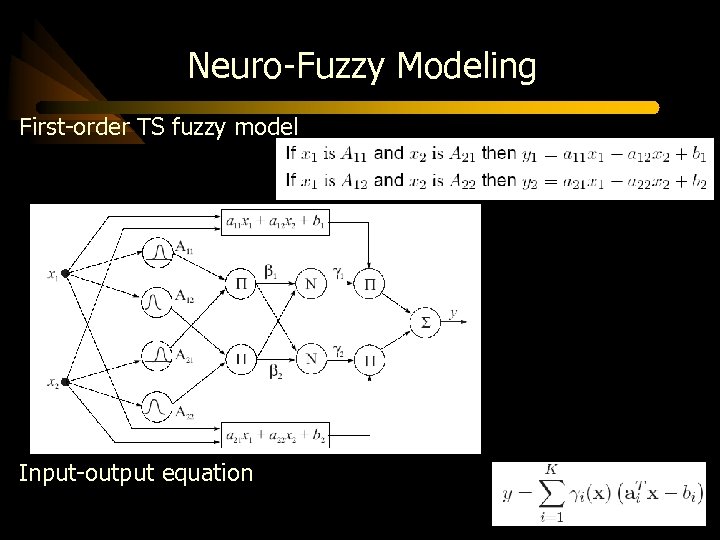
Neuro-Fuzzy Modeling First-order TS fuzzy model Input-output equation

Neuro-Fuzzy Networks - Constructing • • Prior knowledge (can be of a rather approximate nature) Process data Integration of knowledge and data: • Expert knowledge as a collection of if–then rules • (Initial model creation – fine tune using process data) Fuzzy rules are constructed from scratch by using numerical data (expert can confront the information stored in the rule base with his own knowledge) (can modify the rules) (supply additional rules to extend the validity of the model) Comparision the second method with Truly black-box structures possibility to interpret the obtained results

Neuro-Fuzzy Networks – Structure and parameters System identification steps: • Structure identification • Parameter estimation • choice of the model’s structure determines the flexibility of the model in the approximation of (unknown) systems • model with a rich structure can approximate more complicated functions, but, will have worse generalization properties • Good generalization means that a model fitted to one data set will also perform well on another data set from the same process.

Neuro-Fuzzy Networks – Structure and parameters Structure selection process involves: • Selection of input variables • Number and type of membership functions, number of rules (These two structural parameters are mutually related)

Neuro-Fuzzy Networks – Structure and parameters Selection of input variables • Physical inputs • Dynamic regressors (defined by the input and output lags) Typical sources of information: • Prior knowledge • Insight in the process behavior • Purpose of the modeling exercise Automatic data-driven selection can then be used to compare different structures in terms of some specified performance criteria.

Neuro-Fuzzy Networks – Structure and parameters Number and type of membership functions, number of rules • Determine the level of detail (granularity) of the model Typical criteria • Purpose of modeling • Amount of available information (knowledge and data) Automated methods can be used to add or remove membership functions and rules.

Neuro-Fuzzy Networks – Gradient-based learning Zero-order ANFIS model Consequent parameters Jacobian Update law Centers and spreads of the Gaussian membership functions

Neuro-Fuzzy Networks – Hybrid Learning Output-layer parameters in RBF networks can be estimated by linear least-squares (LS) techniques LS methods are more effective than the gradient-based update rule Hybrid methods: • • One-shot least-squares estimation of the consequent parameters Iterative gradient-based optimization of the membership functions Choice of LS estimation method: • • In terms of error minimization is not crucial If consequent parameters are to be interpreted as local models great care must be taken PROBLEM: over-parameterization numerical problems - over-fitting - meaningless parameter estimates

Example – Hybrid Learning Approximation of second-order polynomial by a first-order ANFIS model Membership function for t 1<u<t 2 Model: Output of TS model • Model has four free parameters, while three are sufficient to fit the polynomial

Neuro-Fuzzy Networks – Hybrid Learning To avoid over-parameterization, the basic least-squares criterion can be combined with additional criteria for local fit, or with constraints on the parameter values • • • Local Least-Squares Estimation Constrained Estimation Multi-Objective Optimization

Hybrid Learning - Global LS Estimation

Hybrid Learning - Local LS Estimation While the global solution gives the minimal prediction error, it may bias the estimates of the consequents as parameters of local models. If locally relevant model parameters are required, a weighted LS approach applied per rule should be used. • • The consequent parameters of the individual rules are estimated independently (result is not influenced by the interactions of the rules) Larger prediction error is obtained than with global least squares

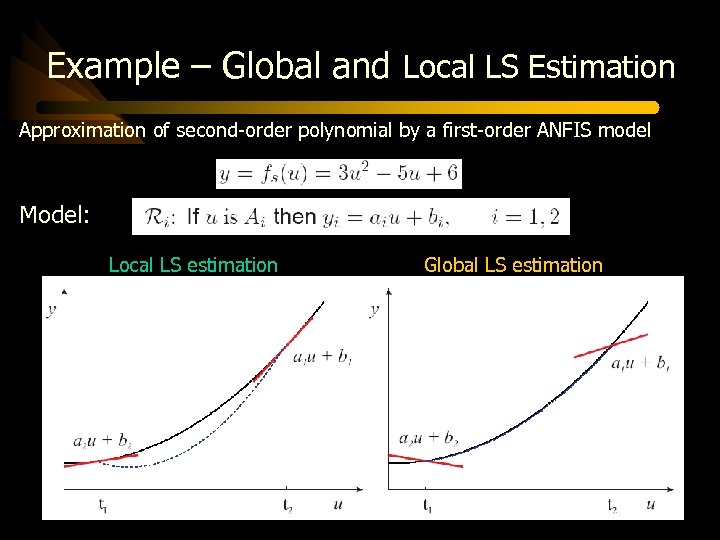
Example – Global and Local LS Estimation Approximation of second-order polynomial by a first-order ANFIS model Model: Local LS estimation Global LS estimation

Hybrid Learning - Constrained Estimation Knowledge about the dynamic system such as its stability, minimal or maximal static gain, or its settling time can be translated into convex constraints on the consequent parameters

Hybrid Learning - Multi-Objective Optimization Minimize the weighted sum of the global and local identification criteria

Initialization of Antecedent Membership Functions For a successful application of gradient-descent learning to the membership function parameters, good initialization is important Initialization methods: • Template-Based Membership Functions • Discrete Search Methods • Fuzzy Clustering

Initialization - Template-Based Membership Functions domains of the antecedent variables are a priori partitioned by a number of membership functions (usually evenly spaced and shaped) severe drawback of this approach is that the number of rules in the model grows exponentially • • • Complexity of the system’s behavior is typically not uniform. Some operating regions can be well approximated by a local linear model, while other regions require a rather fine partitioning. In order to obtain an efficient representation with as few rules as possible, the membership functions must be placed such that they capture the non-uniform behavior of the system.

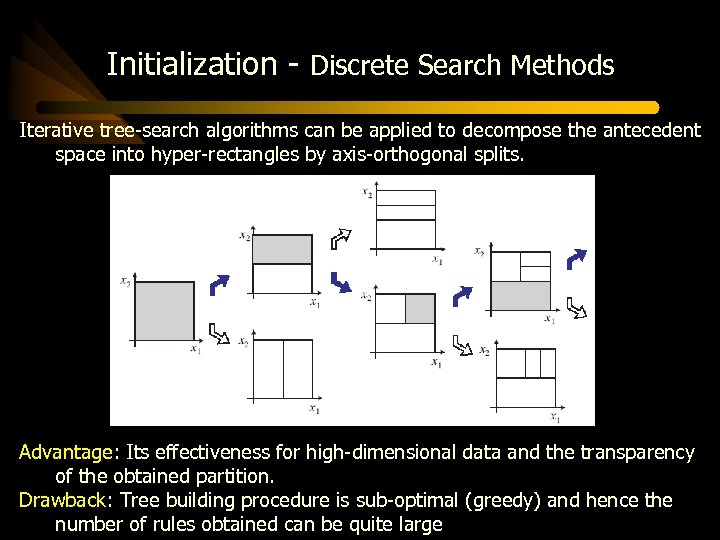
Initialization - Discrete Search Methods Iterative tree-search algorithms can be applied to decompose the antecedent space into hyper-rectangles by axis-orthogonal splits. Advantage: Its effectiveness for high-dimensional data and the transparency of the obtained partition. Drawback: Tree building procedure is sub-optimal (greedy) and hence the number of rules obtained can be quite large

Initialization – Fuzzy Clutering Based on the similarity, data vectors are clustered such that the data within a cluster are as similar as possible, and data from different clusters are as dissimilar as possible. The number of clusters in the data can either be determined a priori or sought automatically by using cluster validity measures and merging techniques

Simulation Example 1. A simple fitting problem of a univariate static function • It demonstrates the typical construction procedure of a neuro-fuzzy model. Numerical results show that an improvement in performance is achieved at the expense of obtaining if-then rules that are not completely relevant as local descriptions of the system. 2. Modeling of a nonlinear dynamic system • Illustrates that the performance of a neuro-fuzzy model does not necessarily improve after training. This is due to overfitting which in the case of dynamic systems can easily occur when the data only sparsely cover the domains

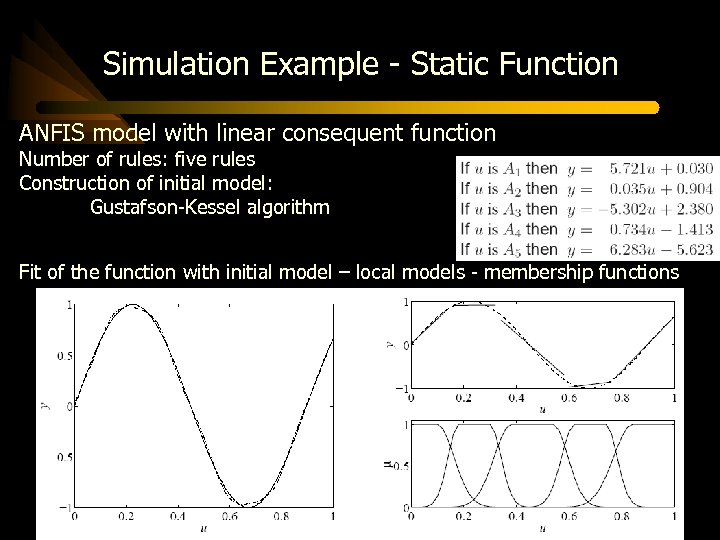
Simulation Example - Static Function ANFIS model with linear consequent function Number of rules: five rules Construction of initial model: Gustafson-Kessel algorithm Fit of the function with initial model – local models - membership functions

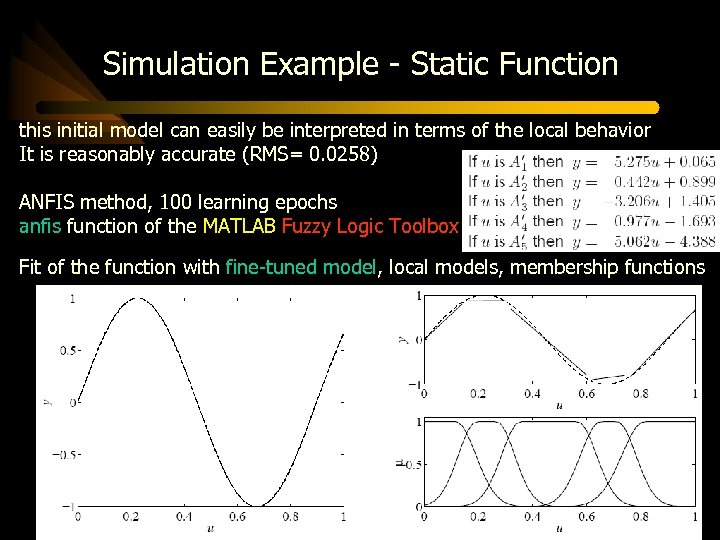
Simulation Example - Static Function this initial model can easily be interpreted in terms of the local behavior It is reasonably accurate (RMS= 0. 0258) ANFIS method, 100 learning epochs anfis function of the MATLAB Fuzzy Logic Toolbox Fit of the function with fine-tuned model, local models, membership functions

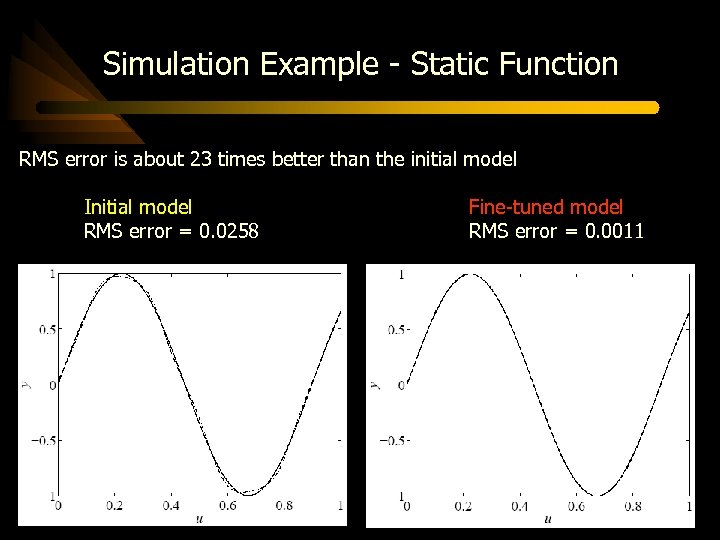
Simulation Example - Static Function RMS error is about 23 times better than the initial model Initial model RMS error = 0. 0258 Fine-tuned model RMS error = 0. 0011

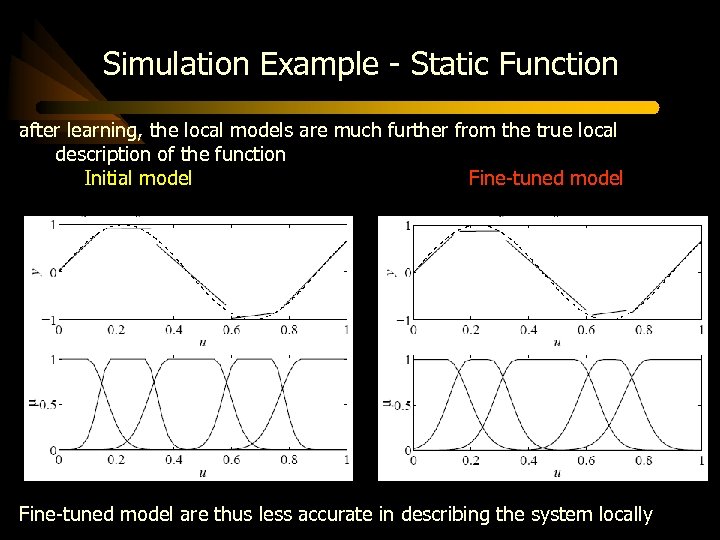
Simulation Example - Static Function after learning, the local models are much further from the true local description of the function Initial model Fine-tuned model are thus less accurate in describing the system locally

Simulation Example – p. H Neutralization Process Influent streams Acid Buffer Base Acid flowrate = cte Buffer flowrate = cte Base stream flowrate Neutralization tank Effluent stream Neutralization tank p. H in the tank

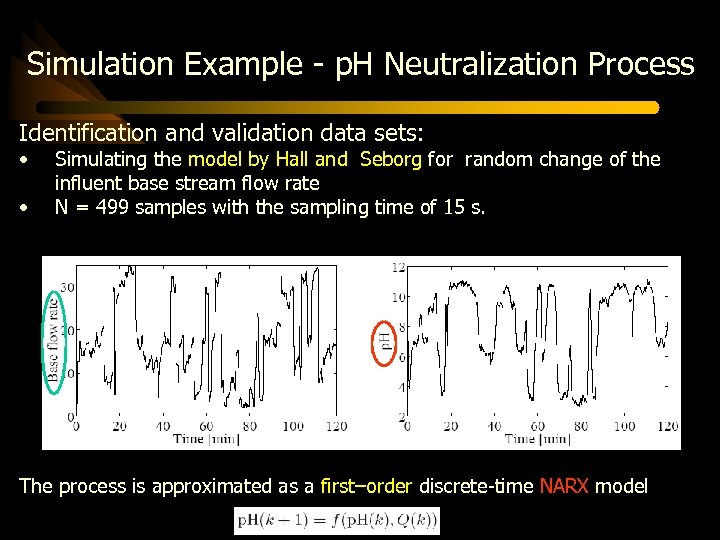
Simulation Example - p. H Neutralization Process Identification and validation data sets: • • Simulating the model by Hall and Seborg for random change of the influent base stream flow rate N = 499 samples with the sampling time of 15 s. The process is approximated as a first–order discrete-time NARX model

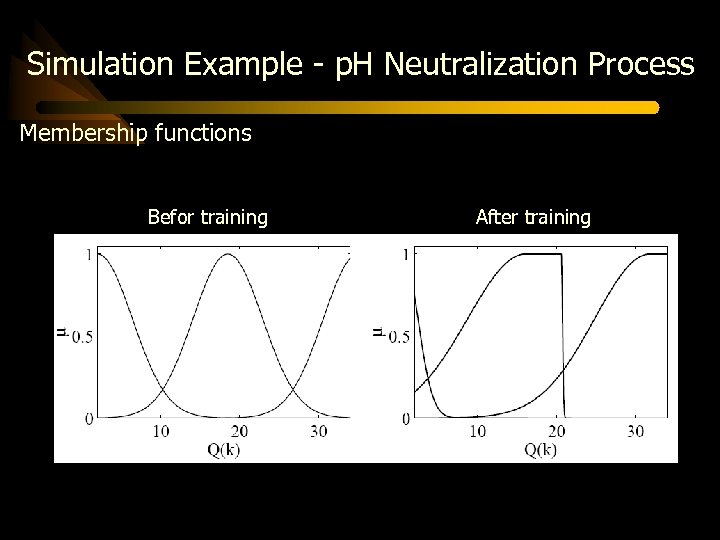
Simulation Example - p. H Neutralization Process Membership functions Befor training After training

Simulation Example - p. H Neutralization Process Rules: Initial Rules: Fine Tuned Rules: after 1000 epochs of hybrid learning using the ANFIS function of the MATLAB Fuzzy Logic Toolbox

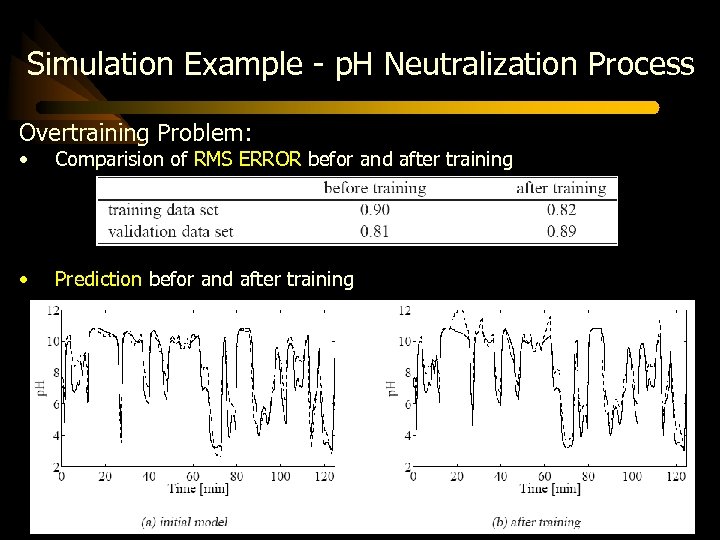
Simulation Example - p. H Neutralization Process Overtraining Problem: • Comparision of RMS ERROR befor and after training • Prediction befor and after training

References [1] Robert Babuska, “Neuro-Fuzzy Methods for Modeling and Identification”, Recent Advances in Intelligent Paradigms and Application, Springer. Verilag, 2002 [2] Robert Babuska, “Fuzzy Modeling and Identification Toolbox User’s Guide - For Use with MATLAB”, 1998. [3] A. Trabelsi, F. Lafont, M. Kamoun and G. Enea, “Identification of Nonlinear Systems by Adaptive Fuzzy Takagi-Sugeno Model”, International Journal of Computational Cognition, Volume 2, Number 3, Pages 137– 153, September 2004. [4] Jantzen, “Neurofuzzy Modelling”, Technical University of Denmark, Department of Automation, 1998.

THANK YOU VERY MUCH For your Attention Presented by: Ali Maleki

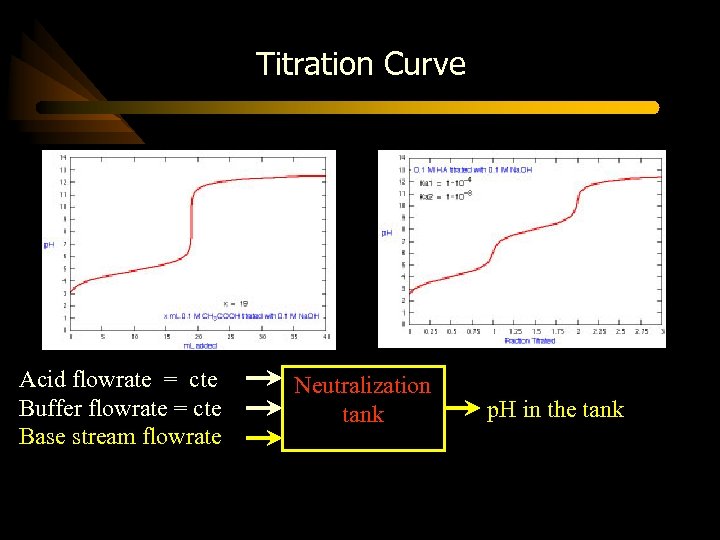
Titration Curve Acid flowrate = cte Buffer flowrate = cte Base stream flowrate Neutralization tank p. H in the tank