Neural Networks Outline

Neural Networks • Outline – – – – Introduction From biological to artificial neurons Self organizing maps Backpropagation network Radial basis functions Associative memories Hopfield networks Other applications of neural networks Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 1

Introduction • Why neural networks? – Algorithms developed over centuries do not fit the complexity of real world problem – The human brain: most sophisticated computer suitable for solving extremely complex problems • Historical knowledge on human brain – Greeks thought that the brain was where the blood is cooled off! – Even till late 19 th century not much was known about the brain and it was assumed to be a continuum of non-structured cells – Phineas Gage’s Story • In a rail accident, a metal bar was shot through the head of Mr. Phineas P. Gage at Cavendish, Vermont, Sept 14, 1848 – Iron bar was 3 feet 7 inches long and weighed 13 1/2 pounds. It was 1 1/4 inches in diameter at one end Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 2

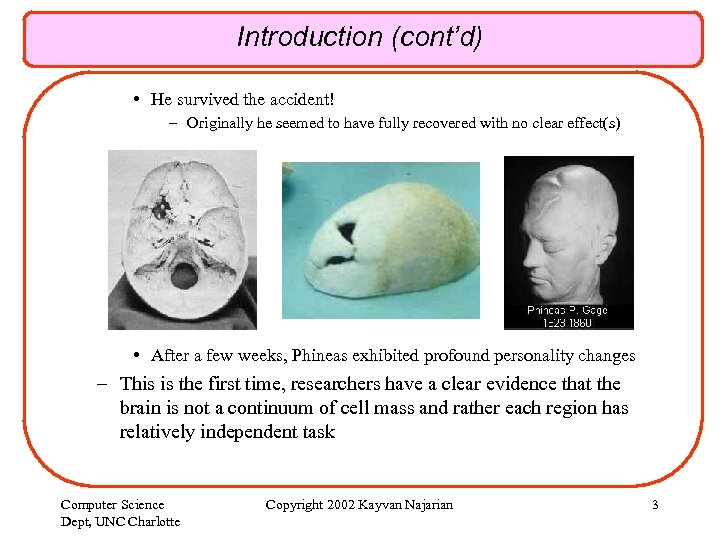Introduction (cont’d) • He survived the accident! – Originally he seemed to have fully recovered with no clear effect(s) • After a few weeks, Phineas exhibited profound personality changes – This is the first time, researchers have a clear evidence that the brain is not a continuum of cell mass and rather each region has relatively independent task Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 3

Introduction (cont’d) • Biological neural networks – 1011 neurons (neural cells) – Only a small portion of these cells are used – Main features • distributed nature, parallel processing • each region of the brain controls specialized task(s) • no cell contains too much information: simple and small processors • information is saved mainly in the connections among neurons Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 4

Introduction (Continued) • learning and generalization through examples • simple building block: neuron – Dendrites: collecting signals from other neurons – Soma (cell body): spatial summation and processing – Axon: transmitting signals to dendrites of other cells Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 5

Introduction (Continued) • biological neural networks: formation of neurons with different connection strengths Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 6

From biological to artificial neural nets • Biological vs. artificial neurons – From biological neuron to schematic structure of artificial neuron • biological: – Inputs – Summation – – of inputs Processing unit Output • artificial: Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 7

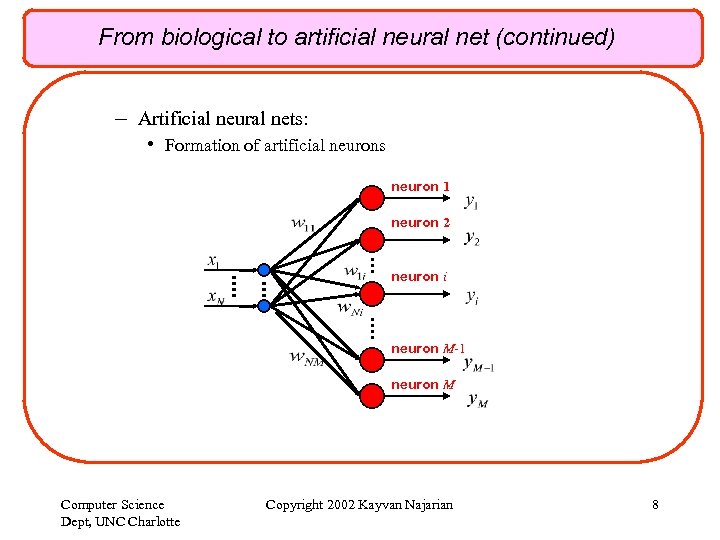From biological to artificial neural net (continued) – Artificial neural nets: • Formation of artificial neurons neuron 1 neuron 2 neuron i neuron M-1 neuron M Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 8

From biological to artificial neural nets (continued) – Multi-layer neural nets: • Serial connection of single layers: – Training: finding the best values of weights wij • Training happens iteratively and through exposing the network to examples: Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 9

From biological to artificial neural nets (continued) – Activation functions: • Hard limiter (binary step): – Role of threshold – Biologically supported – Non-differentiable Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 10

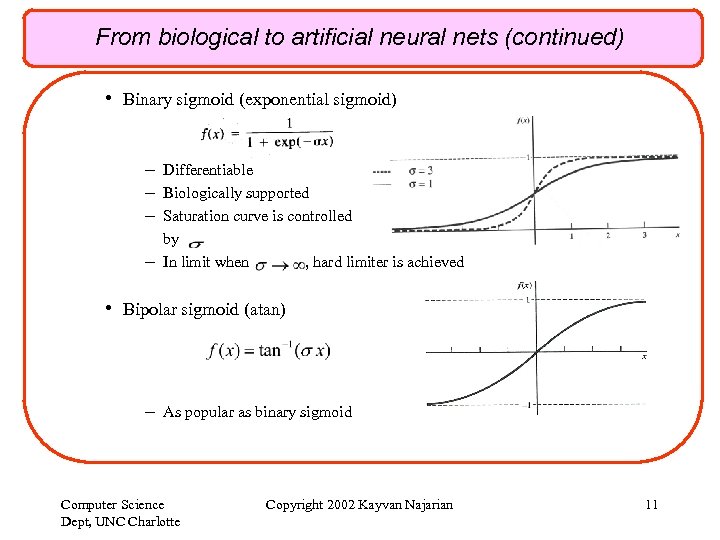From biological to artificial neural nets (continued) • Binary sigmoid (exponential sigmoid) – Differentiable – Biologically supported – Saturation curve is controlled – by In limit when , hard limiter is achieved • Bipolar sigmoid (atan) – As popular as binary sigmoid Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 11

From biological to artificial neural nets (continued) • Supervised Vs Unsupervised Learning – Supervised learning (classification) • • Training data are labeled, i. e the output class of all training data are given Example: recognition of birds and insects – Training set: – Classification: – Unsupervised learning (clustering) • • • Training data are not labeled Output classes must be generated during training Similarity between features of training example creates different classes Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 12

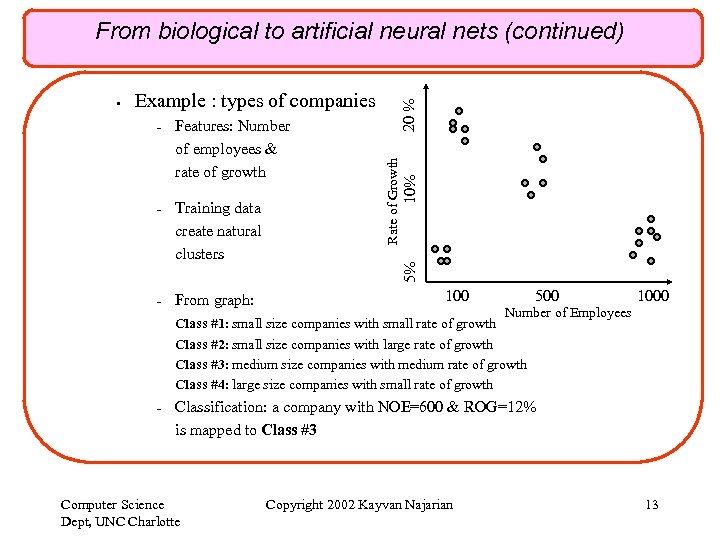– – – Features: Number of employees & rate of growth Training data create natural clusters From graph: 5% – 10% Example : types of companies Rate of Growth • 20 % From biological to artificial neural nets (continued) 100 500 1000 Number of Employees Class #1: small size companies with small rate of growth Class #2: small size companies with large rate of growth Class #3: medium size companies with medium rate of growth Class #4: large size companies with small rate of growth Classification: a company with NOE=600 & ROG=12% is mapped to Class #3 Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 13

From biological to artificial neural nets (continued) – Artificial neural networks as classification tools: • • • If training data are labeled, supervised neural nets are used Supervised leaning normally results to better performance Most successful types of supervised ANNs: – – – Artificial neural networks as clustering tools: • • If training data are not labeled, unsupervised neural nets are used Most successful types of supervised ANNs: – – Multi-layer perceptrons Radial basis function networks Kohonen network Some networks can be trained both in supervised and unsupervised modes Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 14

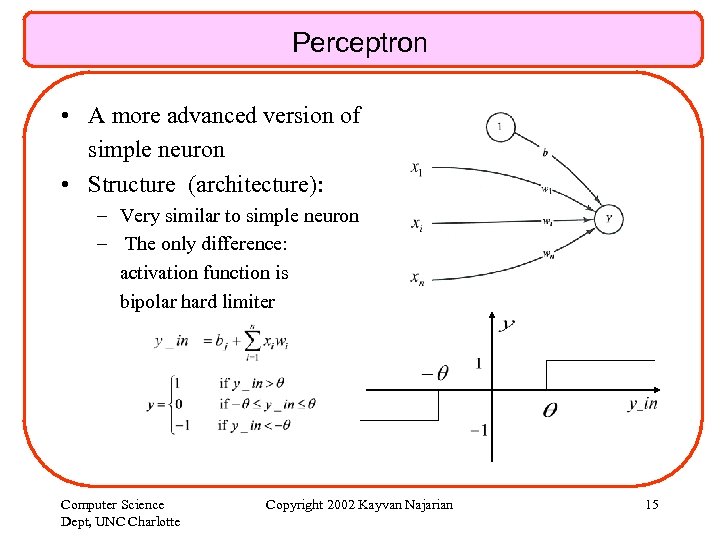Perceptron • A more advanced version of simple neuron • Structure (architecture): – Very similar to simple neuron – The only difference: activation function is bipolar hard limiter Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 15

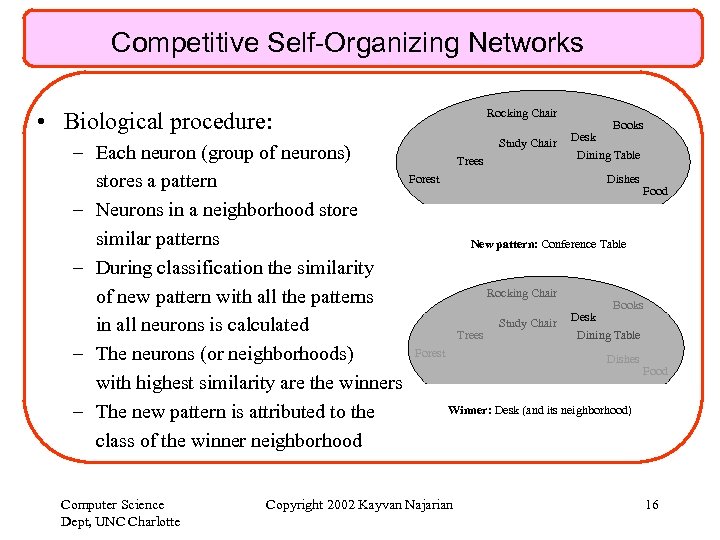Competitive Self-Organizing Networks Rocking Chair • Biological procedure: – Each neuron (group of neurons) stores a pattern – Neurons in a neighborhood store similar patterns – During classification the similarity of new pattern with all the patterns in all neurons is calculated – The neurons (or neighborhoods) with highest similarity are the winners – The new pattern is attributed to the class of the winner neighborhood Computer Science Dept, UNC Charlotte Study Chair Trees Forest Books Desk Dining Table Dishes Food New pattern: Conference Table Rocking Chair Trees Forest Study Chair Books Desk Dining Table Dishes Food Winner: Desk (and its neighborhood) Copyright 2002 Kayvan Najarian 16

Kohonen Self-Organizing Maps • Main idea: placing similar objects close to each other – Example: object classification using one-dimensional array Inputs weight (0 to 1) pencil texture (wood=0, metal =1) size (0 to 1) flies (1) or not (0) airplane chair book wooden house stapler metal desk airplane truck wooden house kite metal desk chair stapler book pencil kite – New pattern: hovercraft • is mapped to the nationhood of truck or airplane Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 17

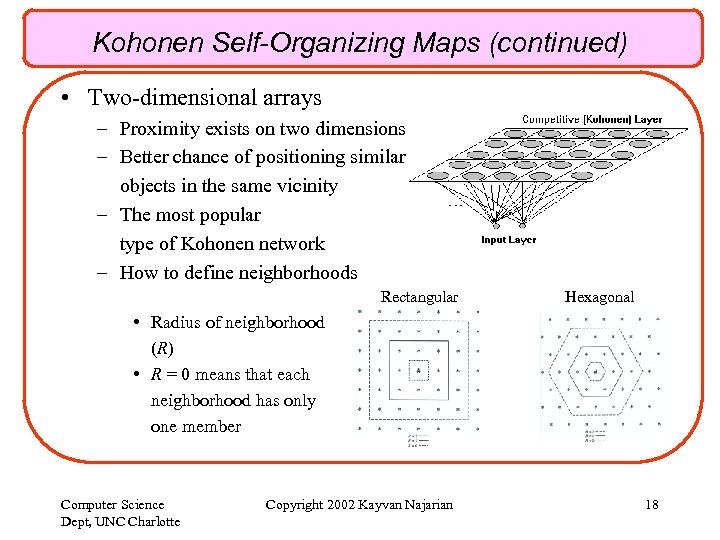Kohonen Self-Organizing Maps (continued) • Two-dimensional arrays – Proximity exists on two dimensions – Better chance of positioning similar objects in the same vicinity – The most popular type of Kohonen network – How to define neighborhoods Rectangular Hexagonal • Radius of neighborhood (R) • R = 0 means that each neighborhood has only one member Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 18

Kohonen Self-Organizing Maps (continued) • Example: two-dimensional array – Classification of objects • • • Objective: clustering of a number of objects 10 input features: # of lines, thickness of lines, angles, . . . Competitive layer is a 2 D-grid of neurons Trained network clusters objects rather successfully Proximity of some objects is not optimal Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 19

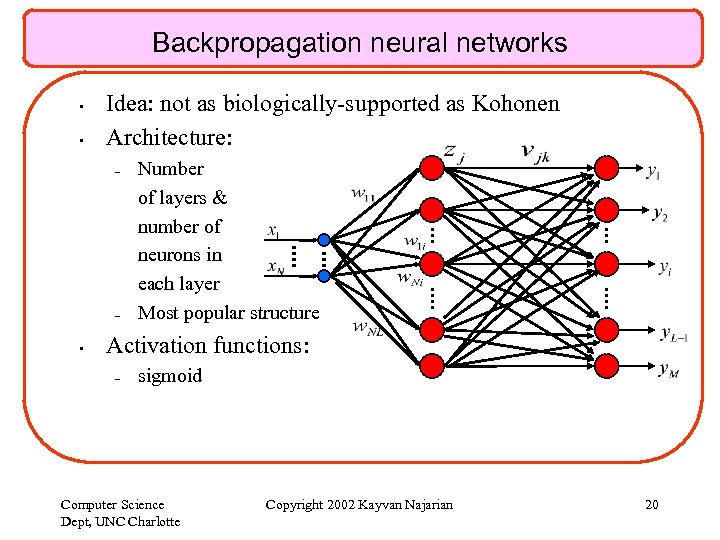Backpropagation neural networks • • Idea: not as biologically-supported as Kohonen Architecture: – – • Number of layers & number of neurons in each layer Most popular structure Activation functions: – sigmoid Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 20

Backpropagation neural networks (continued) • Updating weights: – – – Based on Delta Rule Function to be minimized: Best updating of w. JK is toward the gradient Error of output layer is propagated back towards the input layer Error is calculated at output layer and propagated back towards the input layer As layers receive the backpropagated error, they adjust their weights according to the negative direction of gradient Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 21

Backpropagation neural networks (continued) – Define: – Then: and: – Now: Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 22

Backpropagation neural networks (continued) • Applications: – Time-series analysis and prediction • Problem statement (simplest case): – • • The future value of a signal depends on the previous values of the same signal, i. e. Objective: to use a neural net to estimate function “g” Procedure: – – • Form a number of training points as: Train a backpropagation net to learn the input-output relation Advanced cases: – Computer Science Dept, UNC Charlotte Procedure is similar to the simple case Copyright 2002 Kayvan Najarian 23

Backpropagation neural networks (continued) • Feedforward neural time series models are used in many fields including: – – – • Stock market prediction Weather prediction Control System identification Signal and image processing Signal and image compression Classification: – When a hard limiter is added to the output neurons (only in classification and not during the training phase), backpropagation network is used to classify complex data sets Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 24

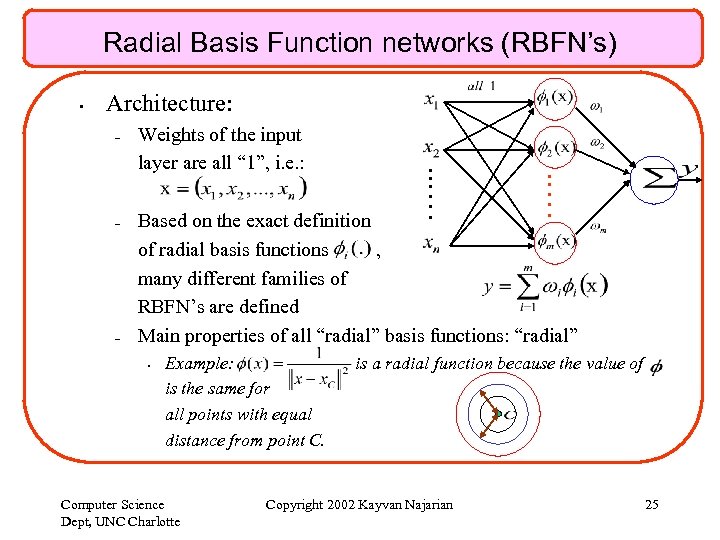Radial Basis Function networks (RBFN’s) – – Weights of the input layer are all “ 1”, i. e. : …. . Architecture: …. . . • Based on the exact definition of radial basis functions , many different families of RBFN’s are defined Main properties of all “radial” basis functions: “radial” – • Example: is the same for all points with equal distance from point C. Computer Science Dept, UNC Charlotte is a radial function because the value of Copyright 2002 Kayvan Najarian 25

RBFN’s (continued) • Basis functions – Gaussian basis functions: • • – Reciprocal Multi-Quadratic (RMQ) functions: • • Coordinates of center: Width parameter: Training: Least Mean Square Techniques Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 26

RBFN’s (continued) • Example: – – – – Trying to approximate a no-linear function using RMQ-RBFN’s Function to be estimated: 135 Training points 19 Basis functions are uniformly centered between -10 and 10 All basis functions have: b = 0. 5 Training method: batch Estimation is rather successful Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 27

Associative Memories • Concept: – Object or pattern A (input) reminds the network of object or pattern B (output) • Heteroassociative Vs. autoassociative memories – If A and B are different, the system is called heteroassociative net • Example: you see a large lake (A) and that reminds you of the Pacific (B) ocean you visited last year – If A and B are the same, the system is called autoassociative net • Example: you see the Pacific ocean for the second time (A) and that reminds you of the Pacific (B) ocean you visited last year Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 28

Associative Memories (continued) • Recognizing new or incomplete patterns – Recognizing patterns that are similar to one of the patterns stored in memory (generalization) • Example: recognizing a football player you haven’t seen before from his clothes – Recognizing incomplete or noisy patterns whose complete (correct) forms were previously stored in memory • Example: recognizing somebody’s face from a picture that is partially torn • Unidirectional Vs. bidirectional memories – Unidirectional: A reminds you of B – Bidirectional: A reminds you of B and B reminds you of A • Many biological neural nets are associative memories Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 29

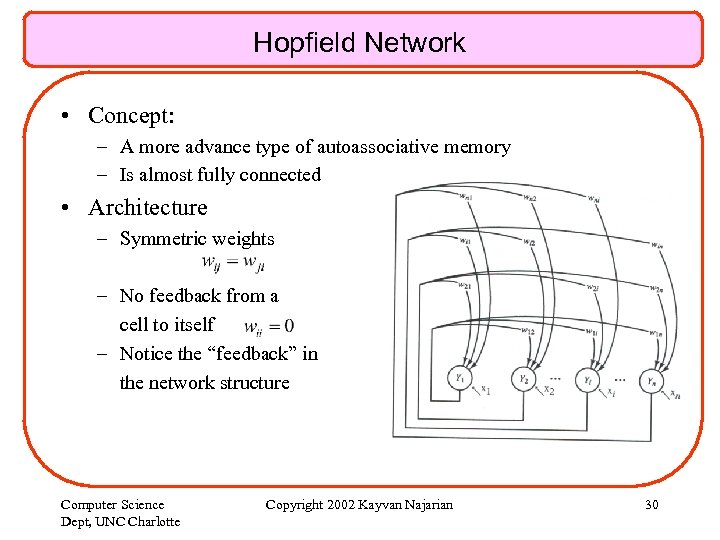Hopfield Network • Concept: – A more advance type of autoassociative memory – Is almost fully connected • Architecture – Symmetric weights – No feedback from a cell to itself – Notice the “feedback” in the network structure Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 30

Bidirectional Associative Memories (BAM) • Concept: – Bidirectional memory: pattern A reminds you of pattern B and pattern B reminds you of pattern A – Is almost fully connected Y 1 • Architecture … Yj … Ym – Symmetric weights – No feedback from a cell to itself – Notice the “feedback” in the network structure Computer Science Dept, UNC Charlotte X 1 … Copyright 2002 Kayvan Najarian Xi … Xn 31

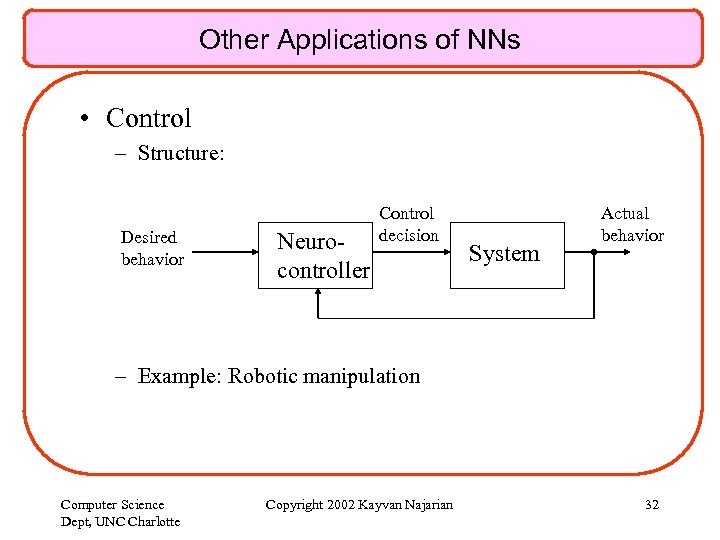Other Applications of NNs • Control – Structure: Desired behavior Neurocontroller Control decision System Actual behavior – Example: Robotic manipulation Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 32

Applications of NNs (continued) • Finance and Marketing – – – Stock market prediction Fraud detection Loan approval Product bundling Strategic planning • Signal and image processing – – Signal prediction (e. g. weather prediction) Adaptive noise cancellation Satellite image analysis Multimedia processing Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 33

Applications of NNs (continued) • Bioinformatics – Functional classification of protein – Functional classification of genes – Clustering of genes based on their expression (using DNA microarray data) • Astronomy – Classification of objects (into stars and galaxies ad so on) – Compression of astronomical data • Function estimation Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 34

Applications of NNs (continued) • Biomedical engineering – Modeling and control of complex biological system (e. g. modeling of human respiratory system) – Automated drug-delivery – Biomedical image processing and diagnostics – Treatment planning • Clustering, classification, and recognition – Handwriting recognition – Speech recognition – Face and gesture recognition Computer Science Dept, UNC Charlotte Copyright 2002 Kayvan Najarian 35