Neural Network to solve Traveling Salesman Problem Amit

Neural Network to solve Traveling Salesman Problem Amit Goyal 01005009 Koustubh Vachhani 01005021 Ankur Jain 01 D 05007

Roadmap n Hopfield Neural Network n Solving TSP using Hopfield Network n Modification of Hopfield Neural Network n Solving TSP using Concurrent Neural Network n Comparison between Neural Network and SOM for solving TSP

Background n Neural Networks n n n Computing device composed of processing elements called neurons Processing power comes from interconnection between neurons Various models are Hopfield, Back propagation, Perceptron, Kohonen Net etc

Associative memory n n n Produces for any input pattern a similar stored pattern Retrieval by part of data Noisy input can be also recognized Original Degraded Reconstruction

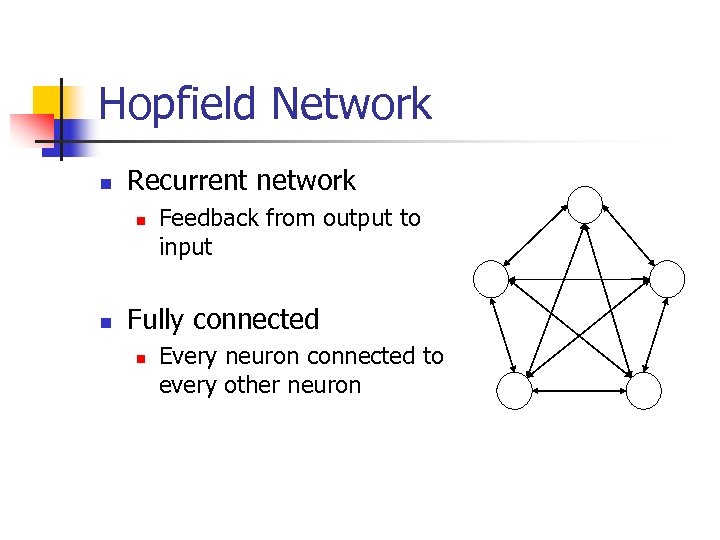
Hopfield Network n Recurrent network n n Feedback from output to input Fully connected n Every neuron connected to every other neuron

Hopfield Network n Symmetric connections n n n Connection weights from unit i to unit j and from unit j to unit i are identical for all i and j No self connection, so weight matrix is 0 diagonal and symmetric Logic levels are +1 and -1

Computation § For any neuron i, at an instant t input is Σj = 1 to n, j≠i wij σj(t) is the activation of the jth neuron § Threshold function θ = 0 § Activation σi(t+1)=sgn(Σj=1 to n, j≠i wijσj(t)) where Sgn(x) = +1 x>0 Sgn(x) = -1 x<0

Modes of operation n Synchronous n n All neurons are updated simultaneously Asynchronous n n Simple : Only one unit is randomly selected at each step General : Neurons update themselves independently and randomly based on probability distribution over time.

Stability n n Issue of stability arises since there is a feedback in Hopfield network May lead to fixed point, limit cycle or chaos n n n Fixed point : unique point attractor Limit cycles : state space repeats itself in periodic cycles Chaotic : aperiodic strange attractor

Procedure n n Store and stabilize the vector which has to be part of memory. Find the value of weight wij, for all i, j such that : <σ1, σ2, σ3 …… σN> is stable in Hopfield Network of N neurons.

Weight learning n Weight learning is given by n n n wij = 1/(N-1) σi σj 1/(N-1) is Normalizing factor σi σj derives from Hebb’s rule n n If two connected neurons are ON then weight of the connection is such that mutual excitation is sustained. Similarly, if two neurons inhibit each other then the connection should sustain the mutual inhibition.

Multiple Vectors n If multiple vectors need to be stored in memory like <σ11, σ21, σ31 …… σN 1> <σ12, σ22, σ32 …… σN 2> ………………. <σ1 p, σ2 p, σ3 p …… σNp> Then the weight are given by: wij = 1/(N-1) Σm=1 to pσim σjm

Energy n n Energy is associated with the state of the system. Some patterns need to be made stable this corresponds to minimum energy state of the system.

Energy function n Energy at state σ’ = <σ1, σ2, σ3 …… σN> n n E(σ’) = -½ Σi Σj≠i wij σiσj Let the pth neuron change its state from σpinitial to σpfinal so n n n Einitial = -½ Σj≠p wpj σpinitial σj + T Efinal = -½ Σj≠p wpj σpfinal σj + T ΔE = Efinal – Einitial T is independent of σp

Continued… ΔE = - ½ (σpfinal - σpinitial ) Σj≠p wpj σj i. e. ΔE = -½ Δσp Σj≠p wpj σj Thus: § § ΔE = -½ Δσp x (netinputp) If p changes from +1 to -1 then Δσp is negative and netinputp is negative and vice versa. So, ΔE is always negative. Thus energy always decreases when neuron changes state.

Applications of Hopfield Nets n Hopfield nets are applied for Optimization problems. n n Optimization problems maximize or minimize a function. In Hopfield Network the energy gets minimized.

Traveling Salesman Problem Given a set of cities and the distances between them, determine the shortest closed path passing through all the cities exactly once.

Traveling Salesman Problem n n n One of the classic and highly researched problem in the field of computer science. Decision problem “Is there a tour with length less than k" is NP - Complete Optimization problem “What is the shortest tour? ” is NP - Hard

Hopfield Net for TSP n n N cities are represented by an N X N matrix of neurons Each row has exactly one 1 Each column has exactly one 1 Matrix has exactly N 1’s σkj = 1 if city k is in position j σkj = 0 otherwise

Hopfield Net for TSP n n For each element of the matrix take a neuron and fully connect the assembly with symmetric weights Finding a suitable energy function E

Determination of Energy Function n E function for TSP has four components satisfying four constraints Each city can have no more than one position i. e. each row can have no more than one activated neuron E 1= A/2 Σk Σi Σj≠i σkj A - Constant

Energy Function (Contd. . ) n Each position contains no more than one city i. e. each column contains no more than one activated neuron E 2= B/2 Σj Σk Σr≠k σkj σrj B - constant

Energy Function (Contd. . ) n There are exactly N entries in the output matrix i. e. there are N 1’s in the output matrix E 3= C/2 (n - ΣkΣi σki)2 C - constant

Energy Function (cont. . ) n Fourth term incorporates the requirement of the shortest path E 4= D/2 ΣkΣr≠kΣj dkr σkj(σr(j+1) + σr(j-1)) where dkr is the distance between city-k and city-r Etotal = E 1 + E 2 + E 3 + E 4

Energy Function (cont. . ) § Energy equation is also given by E= -½ΣkiΣrj w(ki)(rj) σki σrj σki – City k at position i σrj – City r at position j § Output function σki = ½ ( 1 + tanh(uki/u 0)) u 0 is a constant uki is the net input

Weight Value § Comparing above equations with the energy equation obtained previously W(ki)(rj) = -A δkr(1 – δrj) - Bδij(1 – δkr) –C –Ddkr(δj(i+1) + δj(i-1)) § Kronecker Symbol : δkr § § δkr = 1 when k = r δkr = 0 when k ≠ r

Observation n Choice of constants A, B, C and D that provide a good solution vary between n n Always obtain legitimate loops (D is small relative to A, B and C) Giving heavier weights to the distances (D is large relative to A, B and C)

Observation (cont. . ) n Local minima n n Energy function full of dips, valleys and local minima Speed n Fast due to rapid computational capacity of network

Concurrent Neural Network n n n Proposed by N. Toomarian in 1988 It requires N(log(N)) neurons to compute TSP of N cities. It also has a much higher probability to reach a valid tour.

Objective Function § Aim is to minimize the distance between city k at position i and city r at position i+1 Ei = Σk≠rΣrΣi δkiδr(i+1) dkr Where δ is the Kronecers Symbol

Cont … Ei = 1/N 2 Σk≠rΣrΣi dkr Πi= 1 to ln(N) [1 + (2 ע i – 1) σki] [1 + (2µi – 1) σri] Where (2µi – 1) = (2 ע i – 1) [1 – Πj= 1 to i-1 ע i ] Also to ensure that 2 cities don’t occupy same position Eerror = Σk≠rΣr δkr

Solution n n Eerror will have a value 0 for any valid tour. So we have a constrained optimization problem to solve. E = Ei + λ Eerror λ is the Lagrange multiplier to be calculated form the solution.

Minimization of energy function n Minimizing Energy function which is in terms of σki Algorithm is an iterative procedure which is usually used for minimization of quadratic functions The iteration steps are carried out in the direction of steepest decent with respect to the energy function E

Minimization of energy function n Differentiating the energy d. Uki/dt = - δE/ δσki = - δEi/ δσki λδEerror/ δσki dλ/dt = ± δE/ δλ = ± Eerror σki = tanh(αUki) , α – const.

Implementation n Initial Input Matrix and the value of λ is randomly selected and specified At each iteration, new value of σki and λ is calculated in the direction of steepest descent of energy function Iterations will stop either when convergence is achieved or when the number of iterations exceeds a user specified number

Comparison – Hopfield vs Concurrent NN n n n Converges faster than Hopfield Network Probability to achieve valid tour is higher than Hopfield Network Hopfield doesn’t have systematic way to determine the constant terms.

Comparison – SOM and Concurrent NN n n n Data set consists of 52 cities in Germany and its subset of 15 cities. Both algorithms were run for 80 times on 15 city data set. 52 city dataset could be analyzed only using SOM while Concurrent Neural Net failed to analyze this dataset.

Result n n n Concurrent neural network always converged and never missed any city, where as SOM is capable of missing cities. Concurrent Neural Network is very erratic in behavior , whereas SOM has higher reliability to detect every link in smallest path. Overall Concurrent Neural Network performed poorly as compared to SOM.

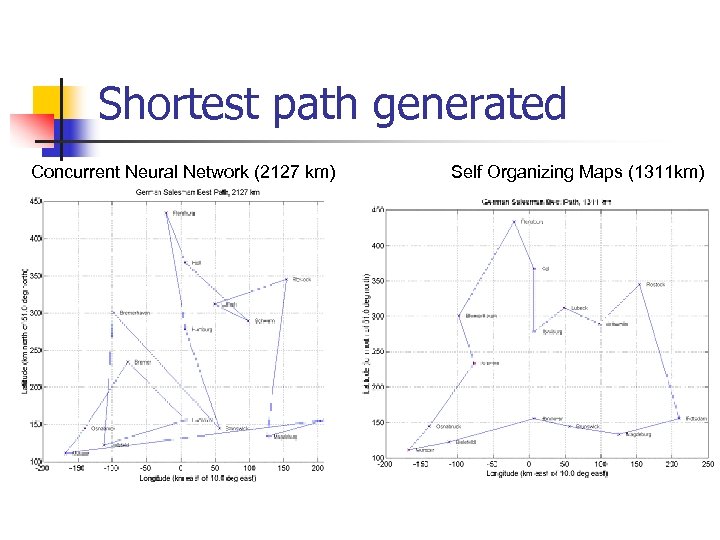
Shortest path generated Concurrent Neural Network (2127 km) Self Organizing Maps (1311 km)

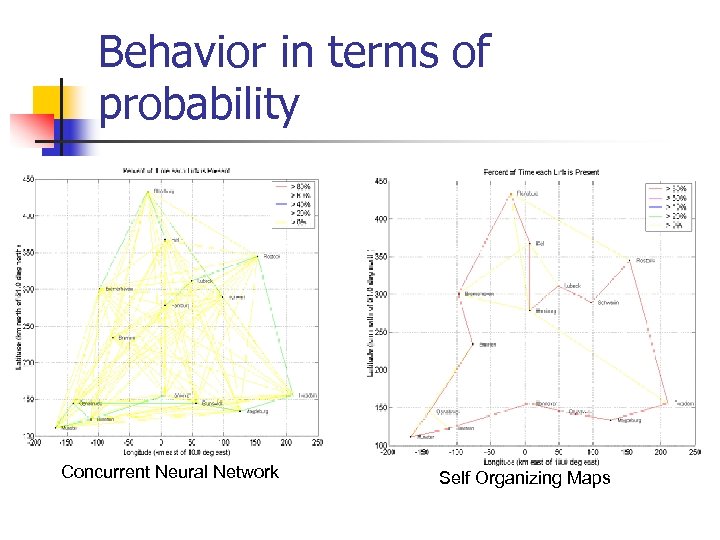
Behavior in terms of probability Concurrent Neural Network Self Organizing Maps

Conclusion n Hopfield Network can also be used for optimization problems. Concurrent Neural Network performs better than Hopfield network and uses less neurons. Concurrent and Hopfield Neural Network are less efficient than SOM for solving TSP.

References n n n N. K. Bose and P. Liang, ”Neural Network Fundamentals with Graphs, Algorithms and Applications”, Tata Mc. Graw Hill Publication, 1996 P. D. Wasserman, “Neural computing: theory and practice”, Van Nostrand Reinhold Co. , 1989 N. Toomarian, “A Concurrent Neural Network algorithm for the Traveling Salesman Problem”, ACM Proceedings of the third conference on Hypercube concurrent computers and applications, pp. 1483 -1490, 1988.

References n n n R. Reilly, “Neural Network approach to solving the Traveling Salesman Problem”, Journals of Computer Science in Colleges, pp. 41 -61, October 2003 Wolfram Research inc. , “Tutorial on Neural Networks”, http: //documents. wolfram. com/applications/neuralnetwor ks/Neural. Network. Theory/2. 7. 0. html, 2004 Prof. P. Bhattacharyya, “Introduction to computing with Neural Nets”, http: //www. cse. iitb. ac. in/~pb/Teaching. html.

NP-complete NP-hard When a decision version of a combinatorial optimization problem is proved to belong to the class of NP-complete problems, which includes well-known problems such as satisfiability, traveling salesman, the bin packing problem, etc. , then the optimization version is NP-hard.

NP-complete NP-hard n n “Is there a tour with length less than k" is NP-complete: It is easy to determine if a proposed certificate has length less than k The optimization problem : "what is the shortest tour? ", is NP-hard Since there is no easy way to determine if a certificate is the shortest.

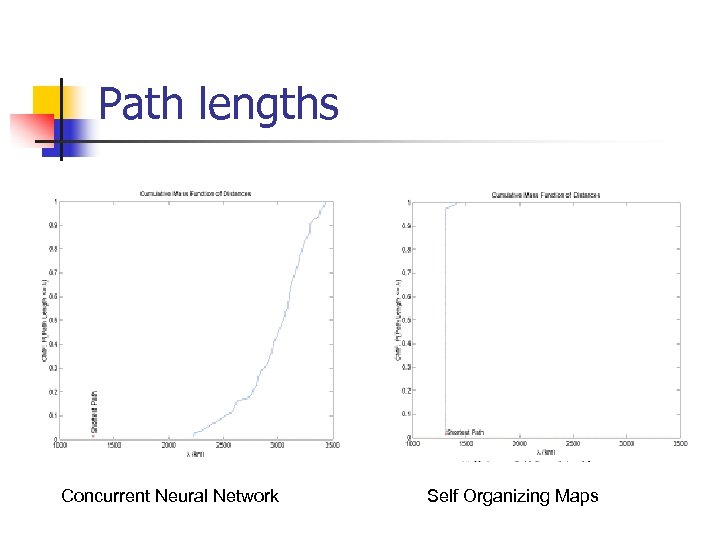
Path lengths Concurrent Neural Network Self Organizing Maps