9d9ad0ec6320c8e080c82268e3fdbea0.ppt
- Количество слайдов: 76

Network Security Essentials Chapter 3 Fourth Edition by William Stallings Lecture slides by Lawrie Brown

Chapter 9 – Public Key Cryptography and RSA Every Egyptian received two names, which were known respectively as the true name and the good name, or the great name and the little name; and while the good or little name was made public, the true or great name appears to have been carefully concealed. —The Golden Bough, Sir James George Frazer

Message Authentication Ø message authentication is concerned with: l l l Ø protecting the integrity of a message validating identity of originator non-repudiation of origin (dispute resolution) the three alternative functions used: l l l hash function message encryption message authentication code (MAC)

Hash Functions Ø condenses arbitrary message to fixed size h = H(M) Ø usually assume hash function is public Ø hash used to detect changes to message Ø want a cryptographic hash function l l computationally infeasible to find data mapping to specific hash (one-way property) computationally infeasible to find two data to same hash (collision-free property)

Two Simple Insecure Hash Functions Ø consider two simple insecure hash functions Ø bit-by-bit exclusive-OR (XOR) of every block l l l Ci = bi 1 xor bi 2 xor. . . xor bim a longitudinal redundancy check reasonably effective as data integrity check Ø one-bit circular shift on hash value l for each successive n-bit block • rotate current hash value to left by 1 bit and XOR block l good for data integrity but useless for security

Hash Function Requirements

Attacks on Hash Functions Ø have brute-force attacks and cryptanalysis Ø a preimage or second preimage attack l find y s. t. H(y) equals a given hash value Ø collision resistance l find two messages x & y with same hash so H(x) = H(y) Ø hence value 2 m/2 determines strength of hash code against brute-force attacks l 128 -bits inadequate, 160 -bits suspect

Secure Hash Algorithm SHA originally designed by NIST & NSA in 1993 Ø was revised in 1995 as SHA-1 Ø US standard for use with DSA signature scheme Ø l l standard is FIPS 180 -1 1995, also Internet RFC 3174 nb. the algorithm is SHA, the standard is SHS based on design of MD 4 with key differences Ø produces 160 -bit hash values Ø recent 2005 results on security of SHA-1 have raised concerns on its use in future applications Ø

Revised Secure Hash Standard Ø NIST issued revision FIPS 180 -2 in 2002 Ø adds 3 additional versions of SHA l SHA-256, SHA-384, SHA-512 Ø designed for compatibility with increased security provided by the AES cipher Ø structure & detail is similar to SHA-1 Ø hence analysis should be similar Ø but security levels are rather higher
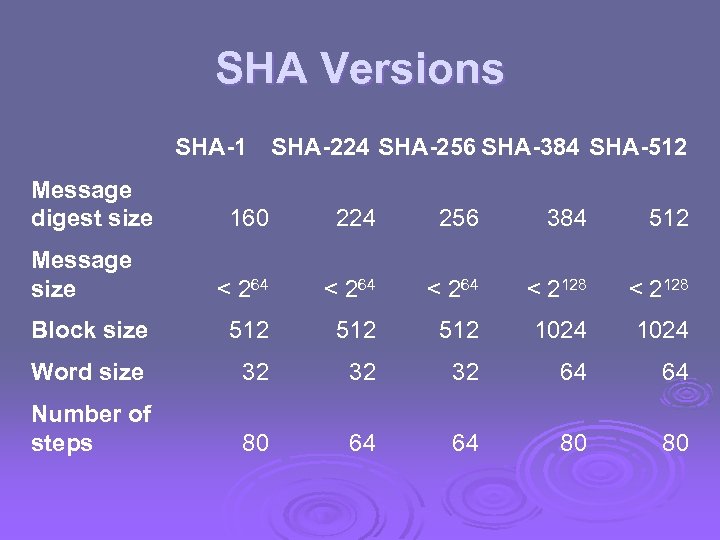
SHA Versions SHA-1 Message digest size SHA-224 SHA-256 SHA-384 SHA-512 160 224 256 384 512 < 264 < 2128 Block size 512 512 1024 Word size 32 32 32 64 64 Number of steps 80 64 64 80 80 Message size
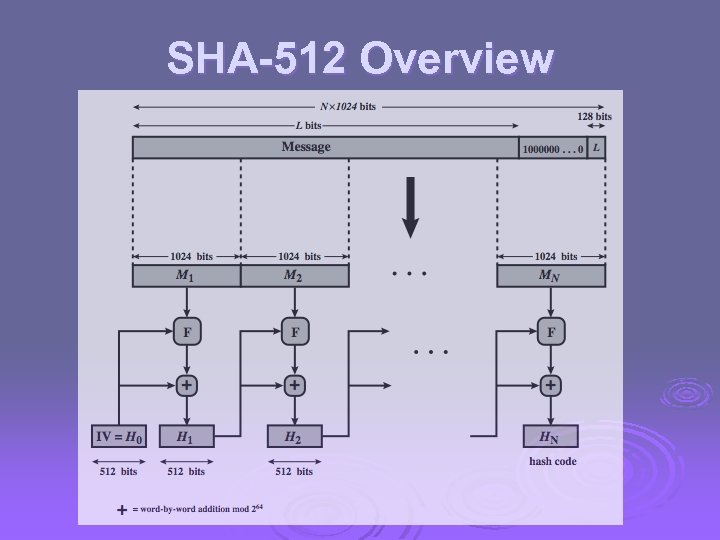
SHA-512 Overview
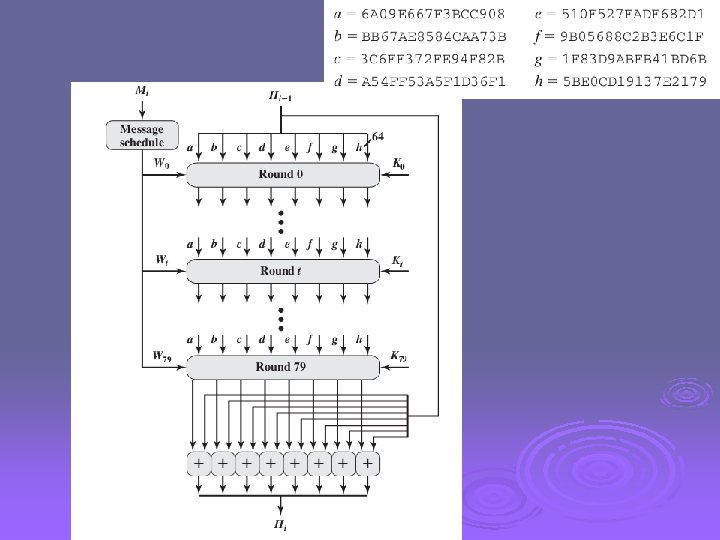

SHA-512 Compression Function Ø heart of the algorithm Ø processing message in 1024 -bit blocks Ø consists of 80 rounds l l l updating a 512 -bit buffer using a 64 -bit value Wt derived from the current message block and a round constant based on cube root of first 80 prime numbers

Keyed Hash Functions as MACs Ø want a MAC based on a hash function l l because hash functions are generally faster crypto hash function code is widely available Ø hash includes a key along with message Ø original proposal: Keyed. Hash = Hash(Key|Message) l some weaknesses were found with this Ø eventually led to development of HMAC

HMAC Design Objectives Ø use, without modifications, hash functions Ø allow for easy replaceability of embedded hash function Ø preserve original performance of hash function without significant degradation Ø use and handle keys in a simple way. Ø have well understood cryptographic analysis of authentication mechanism strength

HMAC specified as Internet standard RFC 2104 Ø uses hash function on the message: Ø HMACK(M)= Hash[(K+ XOR opad) || Hash[(K+ XOR ipad) || M)] ] + is the key padded out to size l where K l opad, ipad are specified padding constants overhead is just 3 more hash calculations than the message needs alone Ø any hash function can be used Ø l eg. MD 5, SHA-1, RIPEMD-160, Whirlpool
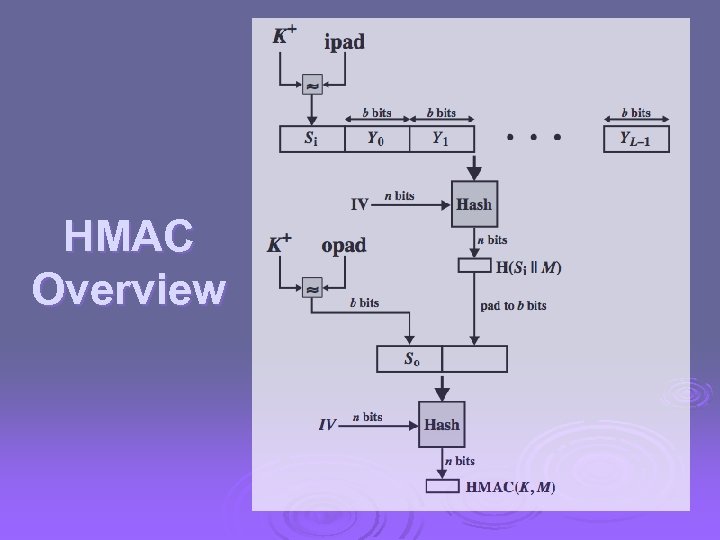
HMAC Overview

HMAC Security Ø proved security of HMAC relates to that of the underlying hash algorithm Ø attacking HMAC requires either: l l brute force attack on key used birthday attack (but since keyed would need to observe a very large number of messages) Ø choose hash function used based on speed verses security constraints

CMAC Ø previously saw the DAA (CBC-MAC) Ø widely used in govt & industry Ø but has message size limitation Ø can overcome using 2 keys & padding Ø thus forming the Cipher-based Message Authentication Code (CMAC) Ø adopted by NIST SP 800 -38 B
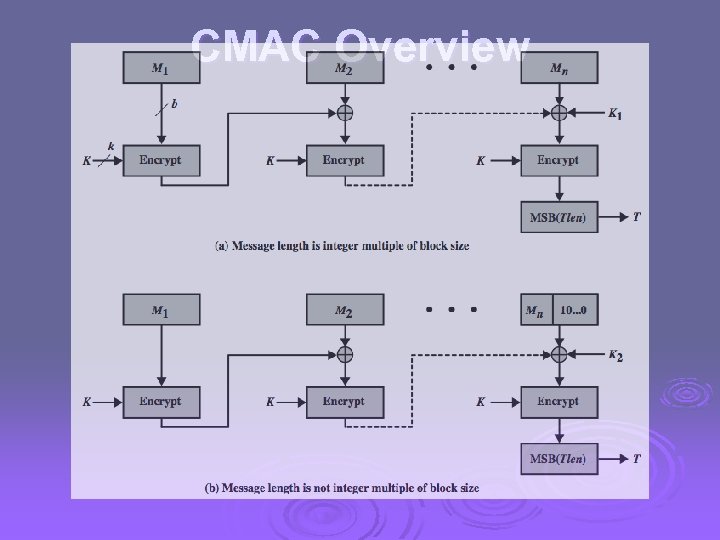
CMAC Overview

Authenticated Encryption Ø simultaneously protect confidentiality and authenticity of communications l often required but usually separate Ø approaches l l Hash-then-encrypt: E(K, (M || H(M)) MAC-then-encrypt: E(K 2, (M || MAC(K 1, M)) Encrypt-then-MAC: (C=E(K 2, M), T=MAC(K 1, C) Encrypt-and-MAC: (C=E(K 2, M), T=MAC(K 1, M) decryption /verification straightforward Ø but security vulnerabilities with all these Ø

Counter with Cipher Block Chaining-Message Authentication Code (CCM) Ø NIST standard SP 800 -38 C for Wi. Fi Ø variation of encrypt-and-MAC approach Ø algorithmic ingredients l l l AES encryption algorithm CTR mode of operation CMAC authentication algorithm Ø single key used for both encryption & MAC
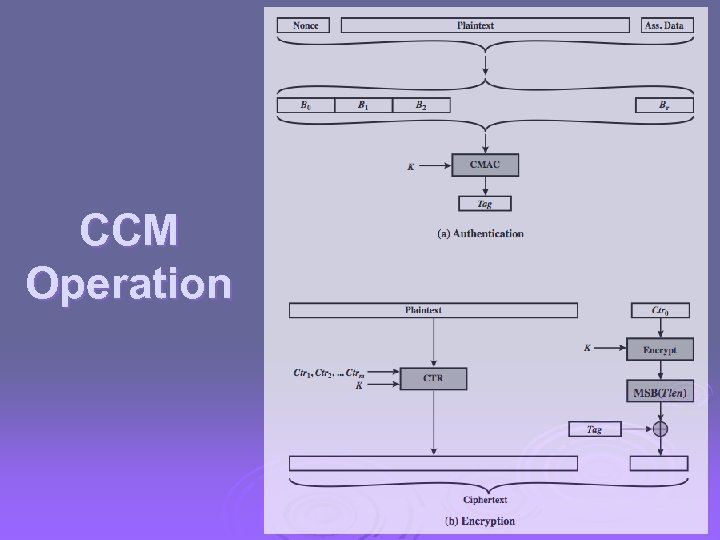
CCM Operation

Private-Key Cryptography Ø Klasik şifreleme 1 anahtar kullanır Ø Alıcı ve gönderen arasında bu anahtar paylaştırılır. Ø Eğer bu anahtar açığa çıkarsa tüm sistem ele geçirilmiş olur Ø Ayrıca simetriktir tüm eşler aynıdır. Ø Bu şekilde alıcının, gönderenden gelmeyen mesajı ondan gelmiş gibi iddaa etme/belirtme ihtimali vardır.

Public-Key Cryptography Ø 2 anahtarlı (açıl ve gizli)PKI yapısı en önemli gelişmedir 3000 yıllık geçimişe nazaran Ø Eşler aynı olmadığı için asimetriktir. Ø Number theory ı kullanır tek yönlü çözülmesi zor olan problemler ile ilgilenir. Ø Gizli anahtar yapısını tamamen kaşldırmaktansa onu tamamlar

Why Public-Key Cryptography? Ø 2 porblemi çözmek için kullanılır: l l Anahtar değiştokuşu– Bir KDC a ihtiyaç duymadan nasıl güvenli iletişim kurulabilir. digital signatures – gerçek gönderenden mesaj değişmeden nasıl gönderilir. Ø Kendi gönderdiğimiz mesajların içinde tam güvenlik. Askeri, Ticari, kişisel Ø public invention due to Whitfield Diffie & Martin Hellman at Stanford Uni in 1976 l Belirli bir grup tarafından daha önceden biliniyordu 1960

Public-Key Cryptography Ø public-key/two-key/asymmetric 2 anahtar şu sebepler için kullanılır : l l a public-key, herkez tarafından bilinebilir, mesajları şifrelemek, ve imzaları doğrulamak için kullanılabilir Ilgili private-key, sadece alıcı tarafından bilinir, mesajı deşifre etmek, ve imzalama (create) signatures için kullanılır Açık anahtardan, gizli anahtarı temin etmek zordur. Ø Asimetriktir : Ø l Mesajı şifreleyen ve mesajı kontrol eden kişi, mesajı deşifre edemez veya bir digital imza atamaz
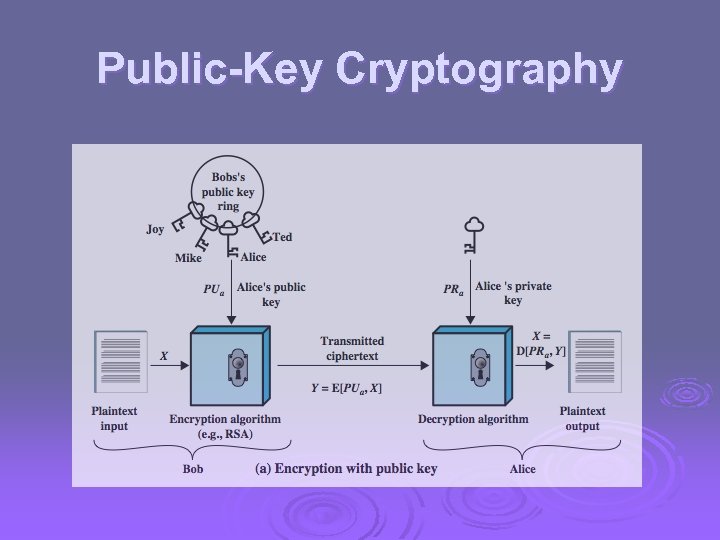
Public-Key Cryptography
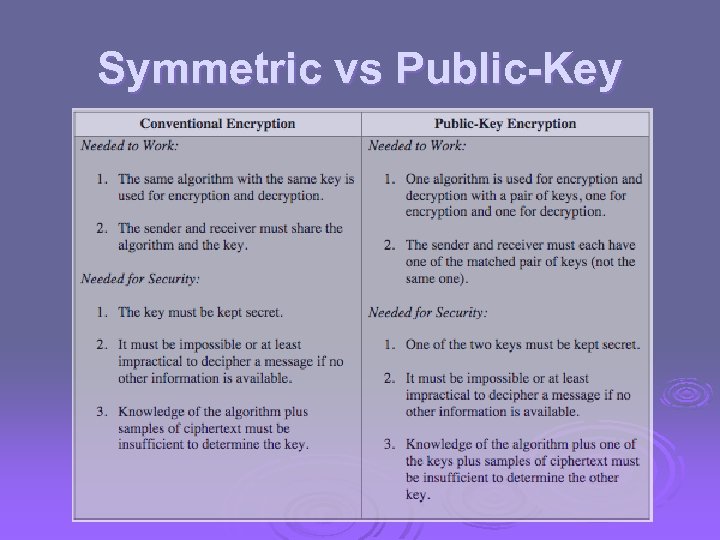
Symmetric vs Public-Key

RSA by Rivest, Shamir & Adleman (RSA) of MIT in 1977 Ø En iyi bilinen ve an fazla kullanılan PKI Ø Matematikteki üssel sonlu alanlar a dayanmaktadır (Galois) ve bir asal sayının tam modülüne dayanmaktadır. Ø l Çok büyük tam sayılar kullanır (eg. 1024 bits) Ø Çok büyük sayıların çarpanlara ayrımasına bağlı güvenliği sahiptir.

RSA En/decryption Ø M mesajını şifrelemek için: l l Alıcının açık anahtarı alınır PU={e, n} C hesaplanır C = Me mod n, 0≤M<n Ø C yi deşifre etmek için alıcı: l l Gizli anahtarını kullanır PR={d, n} M = Cd mod n Ø Mesaj mutlaka modül n den küçük olmalıdır (Gerekli oldulça bloklanır. )

RSA Anahtar seçimi Ø Ø Ø Her bir kullıcı gizli/açık anahtar eşleri üretir: Rastgele iki çok büyük asal sayı seçilir. p, q Bunların çarpımı n modülü oluşturur n=p. q l Hesaplanır ø(n)=(p-1)(q-1) Bir anahtar SEÇİLİR e l 1<e<ø(n), gcd(e, ø(n))=1 (OBEB=gcd) Ø Şifre çözme anahtarını bulmak için aşağıdaki denklem çözülür d bulunur. l e. d=1 mod ø(n) ve 0≤d≤n Ø Açık anahtarı herkeze ver: PU={e, n} Ø Gizli anahtar bilgisini sakla: PR={d, n} Ø

Why RSA Works Ø Eular teoremine göre: l Ø aø(n)mod n = 1 where gcd(a, n)=1 RSA da l l n=p. q ø(n)=(p-1)(q-1) e ve d ters mod ø(n) olacak şekilde dikkatlice seçilir. böylece e. d=1+k. ø(n) bir k değeri için eşit olur Ø hence : Cd = Me. d = M 1+k. ø(n) = M 1. (Mø(n))k = M 1. (1)k = M 1 = M mod n

RSA Example - Key Setup 1. 2. 3. 4. 5. 6. 7. Select primes: p=17 & q=11 Calculate n = pq =17 x 11=187 Calculate ø(n)=(p– 1)(q-1)=16 x 10=160 Select e: gcd(e, 160)=1; choose e=7 Determine d: de=1 mod 160 and d < 160 Value is d=23 since 23 x 7=161= 10 x 160+1 Publish public key PU={7, 187} Keep secret private key PR={23, 187}

RSA Example - En/Decryption Ø Örnek RSA encryption/decryption Ø Mesaj M = 88 (nb. 88<187) Ø şifreleme: C = 887 mod 187 = 11 Ø Deşifreleme: M = 1123 mod 187 = 88

Diffie-Hellman Key Exchange Ø Ilk önerilen first PKI alt yapısıdır Ø by Diffie & Hellman in 1976 along with the exposition of public key concepts l note: now know that Williamson (UK CESG) secretly proposed the concept in 1970 Ø Sonradan kullanılacak şifreleme için anahtar değiştokuşuna olanak saülayan pratik bir yöntemdir. Ø used in a number of commercial products

Diffie-Hellman Key Exchange Ø a Açık anahtar dağıtım şeması l l l genel bir mesajı göndermek için kullanılmaz Fakat ortak bir anahar için kullanılabilir. Sadece iki tarafından bilinir Anahtarın değeri katılanlara bağlıdır. (açık ve gizli anahtar konumlarına ) Ø Sonlu alanların üssel gösterimine bağlıdır. (Galois) alanı field (modulo a prime or a polynomial) - easy Ø Gücenlik ayrık logaitmanın hesabının yapılmasınını zor olmasına bağlıdır (similar to factoring) – hard Ø

Diffie-Hellman Setup Ø Tüm kullanıcılar parametrelerde anlaşırlar: l l Çok büyük bir asal tamsayı yada polinom q a, mod q ya göre temel kökü • primitive root a is a number whose powers successively generate all the elements mod q Ø Her bir kullanıcı (ör. A) l l anahtar üretirler Bir gizli anahtar SEÇ (number): x. A < q Onun açık anahtarını hesapla public key x • y. A = a A mod q Ø Her bir kullanıcı y. A açık anahtar haline getirir • For an attacker monitoring the exchange of the y's to recover either of the x's, they'd need to solve the discrete logarithm problem, which is hard

Diffie-Hellman Key Exchange Ø Ortak bir oturum anahtarı A & B için KAB: x x KAB = a A. B mod q x. B = y. A mod q ( B hesaplayabilir) x. A = y. B mod q ( A hesaplayabilir) KAB gizli anahtar şifrelemesi için oturum anahtarı olarak kullanılır Ø Eğer Alive ve Bob aynı public anahtarları kullandıkça bu gizli anahtarı sonradan gene haberleşmek için kullanabilirler Ø Saldırganın bir X e ihtiyacı vardır ve ayrık logaritmayı çözmelidirler Ø

Diffie-Hellman Example Alice & Bob anahtar değiş tokuşu yağmak isterler: Bir asal sayıda anlaşırlar q=353 ve a=3 Ø Bir gizli ANAHTAR SEÇERLER: Ø Ø l Ø Karşılık gelen açıkanahtarları hesaplamak için : l l Ø A x. A=97, B x. B=233 97 y A= 3 mod 353 = 40 (Alice) 233 y B= 3 mod 353 = 248 (Bob) Paylaşılan açık anahtarın hesaplanması: l l KAB= x. A y. B x. B y. A 97 mod 353 = 248 mod 353= 160 (Alice) 233 mod 353 = 40 mod 353= 160 (Bob)

Key Exchange Protocols Ø Kullanıcılar her iletişim kurmak istediklerinde yeni anahtar çiftleri D-H kullarak üretebilirler Ø Kullanıcılar herkeze açık bir dizin içinde DH anahtarları koylabilir. Ø Hepsi meet-in-the-Middle Attack a karşı zayıftır. Ø anahtarların denetimi lazım

Man-in-the-Middle Attack 1. 2. 3. 4. 5. 6. 7. Darth 2 tane private / public keys üreterek başlar Alice Bob a açık anahtarını gönderir Darth araya girer ve ilk üretiği açık anahtarı BOB a gönderir. Dart ayrıca Alice ile paylaşılan bir anahtar da anlaşır Bob açık anahtarı alır ve paylaşılan bir anahtar üretir. (Fakat alice yerine Darth ile) Bob “Alice” açık anahtarını gönderir. Darth Alice giden açık anahtarı alır. Darth BOB ile arasında bir paylaştıkları bir anahtar üretir (Alice zanneder= Darth Alice & Bob arasındaki tüm iletişimi inceler / değiştirir

1. 2. 3. 4. 5. 6. 7. Darth – Yd 1, Xd 1 – Yd 2, Xd 2 Alice---> “Bob” Ya Darth -->Bob Yd 1. K 2 = (YA )^XD 2 mod q Bob -->Yd 1 ile K 1=(YD 1 )^ XB mod q Bob---> “Alice” Yb Darth-->Alice Yd 2. K 2=(YD 2 )^ XA mod q. Alice-->Yd 2 ile K 2=(YD 2 )^ XA mod q.

Digital Signatures Ø have looked at message authentication l but does not address issues of lack of trust Ø digital signatures provide the ability to: l l l verify author, date & time of signature authenticate message contents be verified by third parties to resolve disputes Ø hence include authentication function with additional capabilities
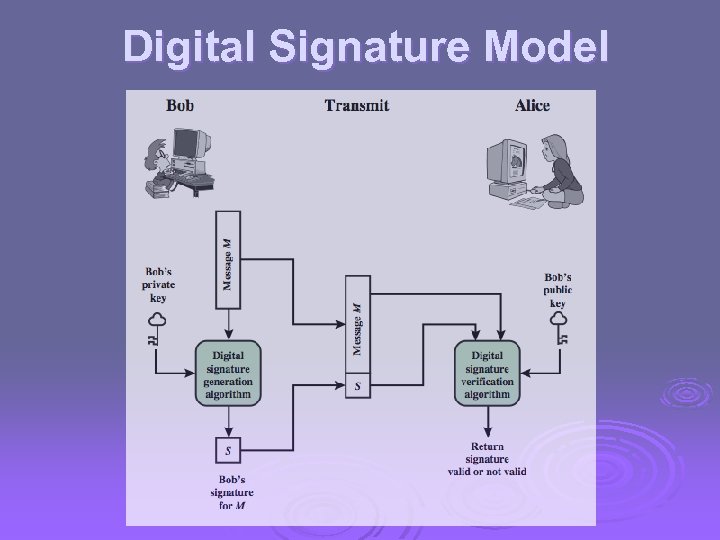
Digital Signature Model
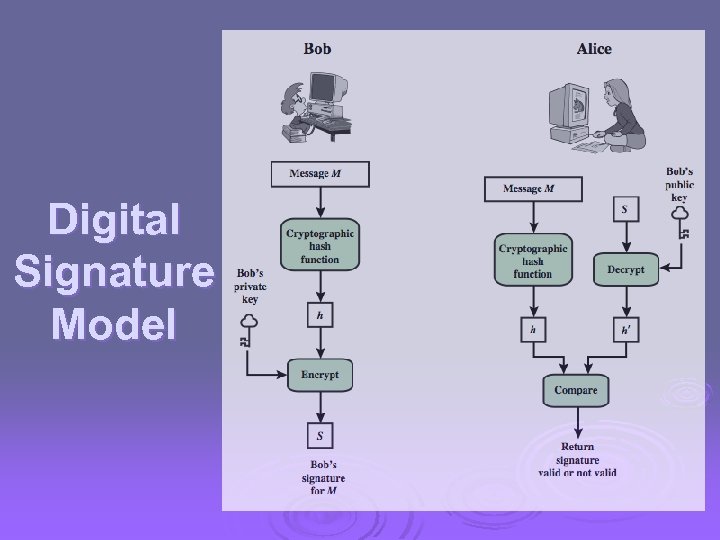
Digital Signature Model

Digital Signatures Lets receiver verify the message is authentic l l Symmetric-Key signatures » Public-Key signatures » Message digests » The birthday attack » CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011

Digital Signatures (1) Requirements for a signature: l l l Receiver can verify claimed identity of sender. Sender cannot later repudiate contents of message. Receiver cannot have concocted message himself. CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011
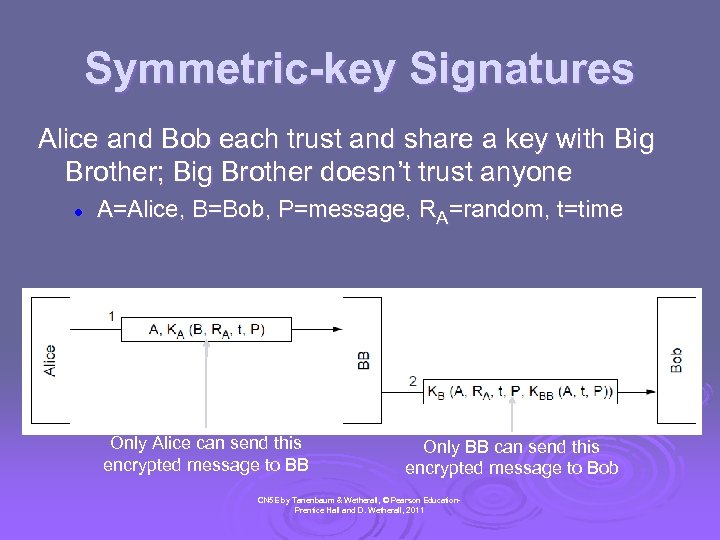
Symmetric-key Signatures Alice and Bob each trust and share a key with Big Brother; Big Brother doesn’t trust anyone l A=Alice, B=Bob, P=message, RA=random, t=time Only Alice can send this encrypted message to BB Only BB can send this encrypted message to Bob CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011
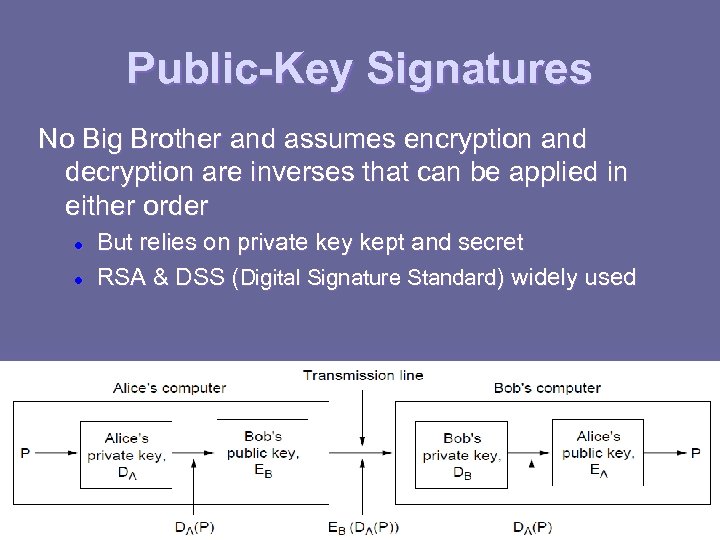
Public-Key Signatures No Big Brother and assumes encryption and decryption are inverses that can be applied in either order l l But relies on private key kept and secret RSA & DSS (Digital Signature Standard) widely used CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011

Message Digests (1) Message Digest (MD) converts arbitrary-size message (P) into a fixed-size identifier MD(P) with properties: l l Given P, easy to compute MD(P). Given MD(P), effectively impossible to find P. Given P no one can find P′ so that MD(P′) = MD(P). Changing 1 bit of P produces very different MD. Message digests (also called cryptographic hash) can “stand for” messages in protocols, e. g. , authentication l l Example: SHA-1 160 -bit hash, widely used Example: MD 5 128 -bit hash – now known broken CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011
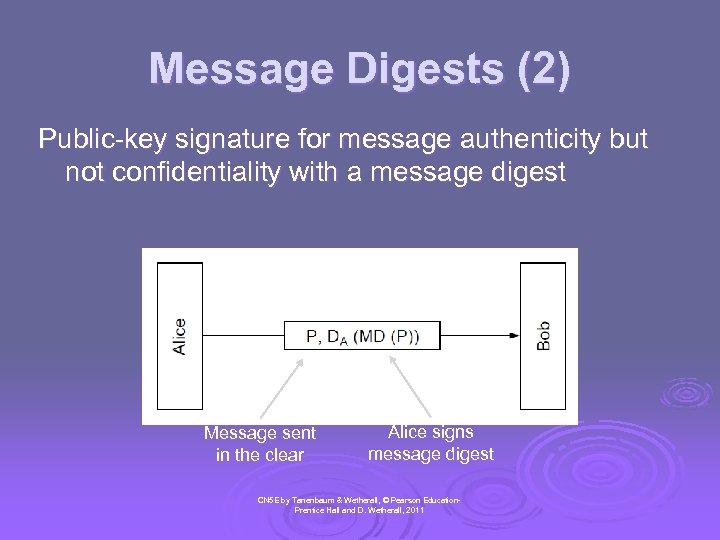
Message Digests (2) Public-key signature for message authenticity but not confidentiality with a message digest Message sent in the clear Alice signs message digest CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011
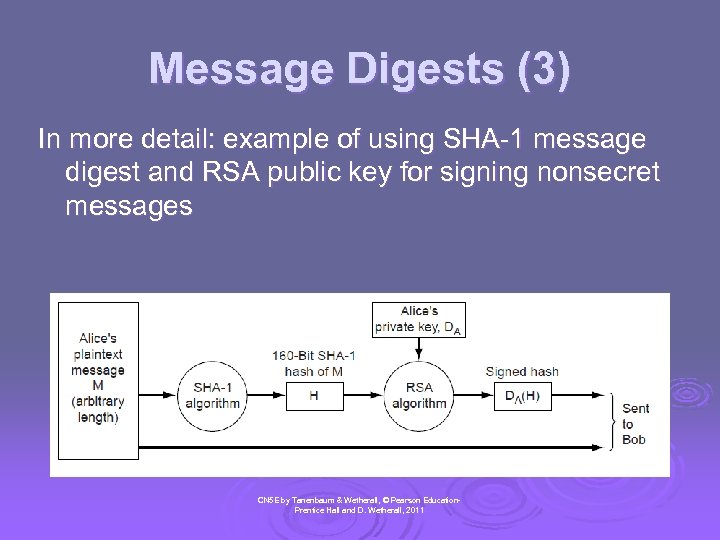
Message Digests (3) In more detail: example of using SHA-1 message digest and RSA public key for signing nonsecret messages CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011

Message Digests (4) SHA-1 digests the message 512 bits at a time to build a 160 -bit hash as five 32 -bit components SHA-1 Message in 512 -bit blocks CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011 Five 32 -bit hashes output

Birthday Attack How hard is it to find a message P′ that has the same message digest as P? l Such a collision will allow P′ to be substituted for P! Analysis: N l N bit hash has 2 possible values N l Expect to test 2 messages given P to find P′ N/2 messages to find a collision l But expect only 2 l This is the birthday attack CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011

Management of Public Keys We need a trusted way to distribute public keys l l l Certificates » X. 509, the certificate standard » Public Key infrastructures » CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011
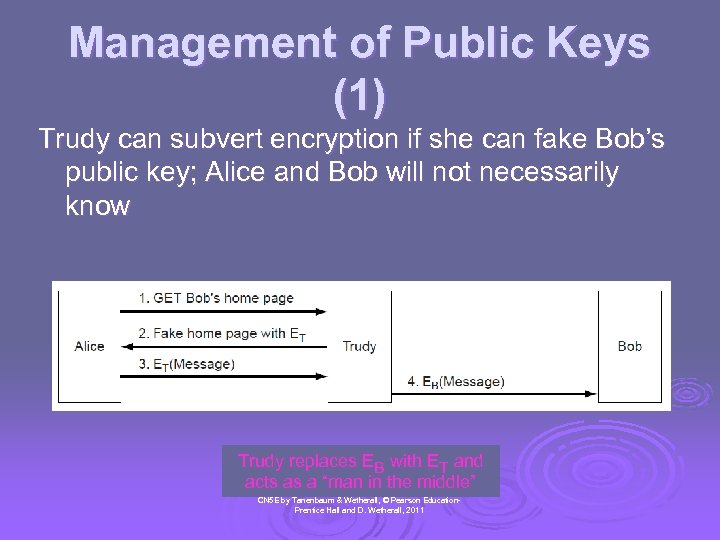
Management of Public Keys (1) Trudy can subvert encryption if she can fake Bob’s public key; Alice and Bob will not necessarily know Trudy replaces EB with ET and acts as a “man in the middle” CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011

Certificates CA (Certification Authority) issues signed statements about public keys; users trust CA and it can be offline A possible certificate CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011
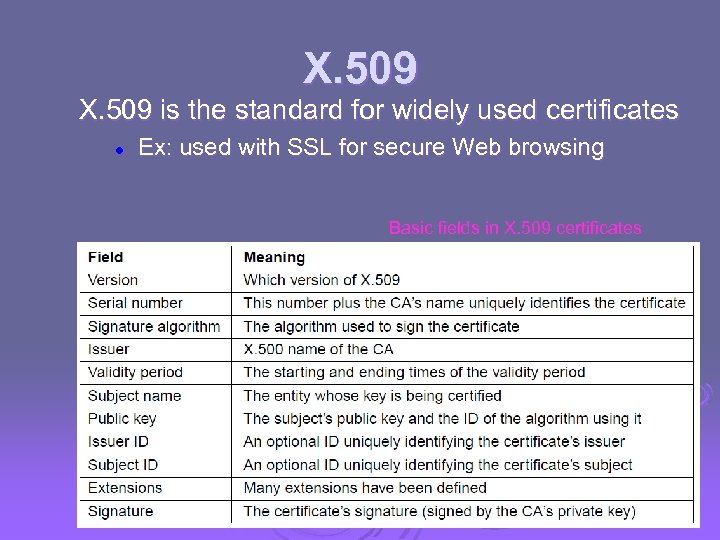
X. 509 is the standard for widely used certificates l Ex: used with SSL for secure Web browsing Basic fields in X. 509 certificates CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011
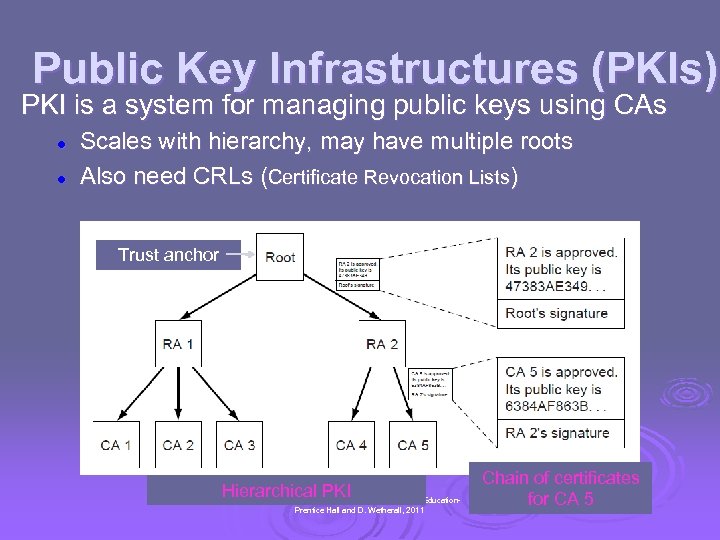
Public Key Infrastructures (PKIs) PKI is a system for managing public keys using CAs l l Scales with hierarchy, may have multiple roots Also need CRLs (Certificate Revocation Lists) Trust anchor Hierarchical PKI CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011 Chain of certificates for CA 5

Authentication Protocols Authentication verifies the identity of a remote party l l l Shared Secret Key » Diffie-Hellman Key Exchange » Key Distribution Center » Kerberos » Public-Key Cryptography » CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011

Authorization vs Authentication Authorization : process permitted to do smth. • Authentication: if you are actually communicating with a specific process. • • Hey I’m Your Boss, delete that debt file of Trudy. • • Authentication : Are you really Boss Authorization : is Boss really allowed to such an activity
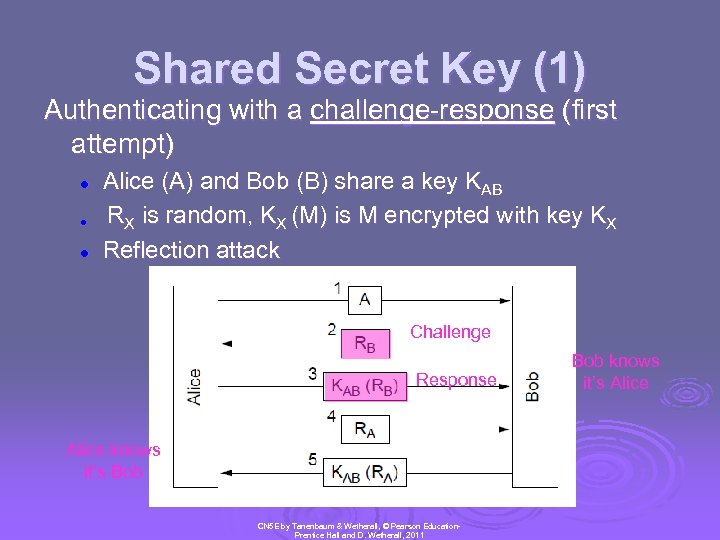
Shared Secret Key (1) Authenticating with a challenge-response (first attempt) l l l Alice (A) and Bob (B) share a key KAB RX is random, KX (M) is M encrypted with key KX Reflection attack Challenge Response Alice knows it’s Bob CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011 Bob knows it’s Alice
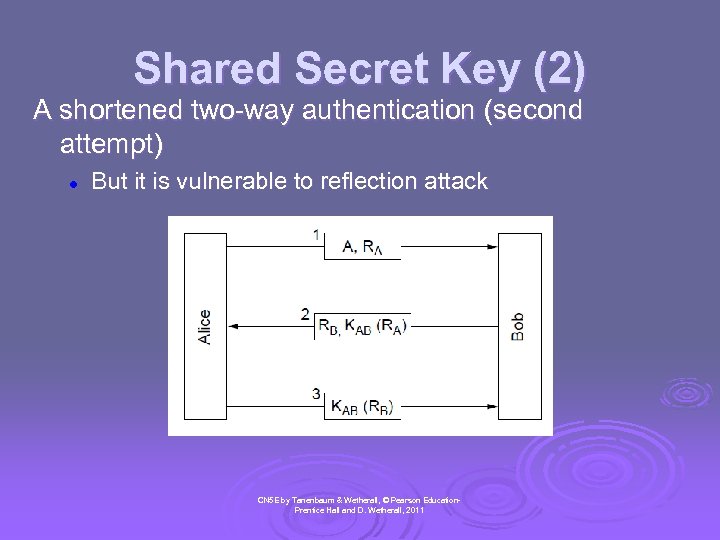
Shared Secret Key (2) A shortened two-way authentication (second attempt) l But it is vulnerable to reflection attack CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011
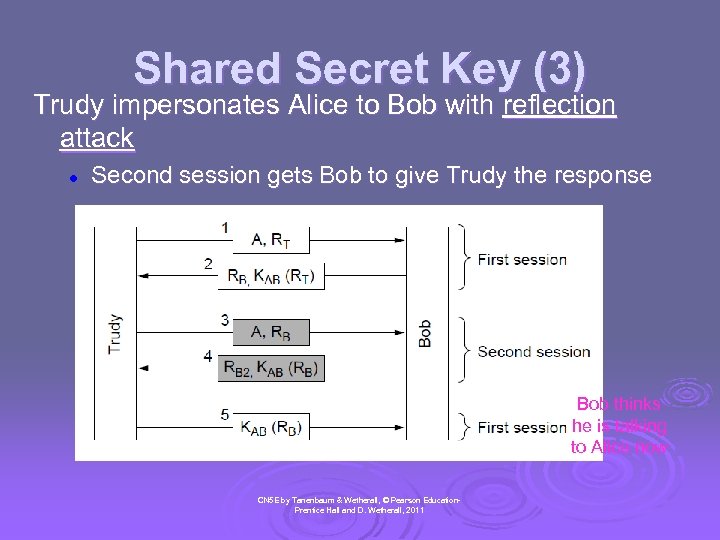
Shared Secret Key (3) Trudy impersonates Alice to Bob with reflection attack l Second session gets Bob to give Trudy the response Bob thinks he is talking to Alice now CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011

Common pitfalls Cevap veren kendini tanıtmadan önce, onun hakkında doğrulayıcı bilgiye sahip olmak. 2. Iletişimi başlatan ve cevap verenin kanıtlamak için farklı anahtarlar kullanmasını sağla. Bu iki farklı anahtar olması anlamına gelsede 3. Iletişimi başlatan ve cevap verenin, cevapları farklı doğrulamak için seçtikleri challengeları farklı kümelerden seçmelidir 1.
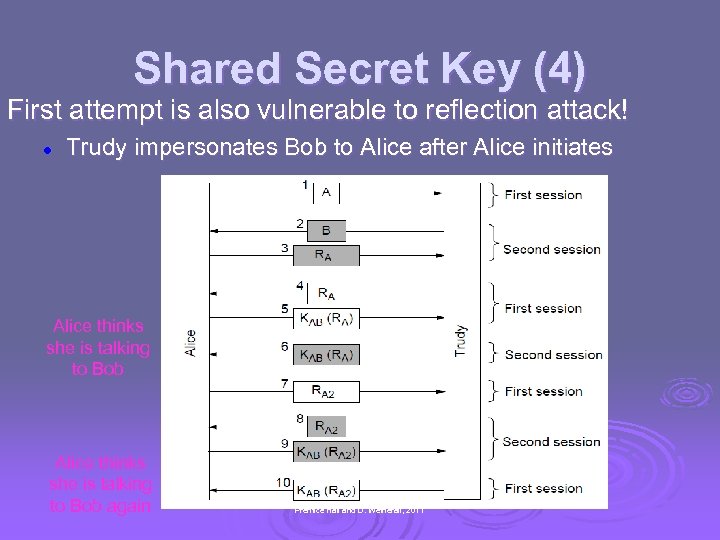
Shared Secret Key (4) First attempt is also vulnerable to reflection attack! l Trudy impersonates Bob to Alice after Alice initiates Alice thinks she is talking to Bob again CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011

Shared Secret Key (5) Moral: Designing a correct authentication protocol is harder than it looks; errors are often subtle. General design rules for authentication: 1. 2. 3. 4. Have initiator prove who she is before responder Initiator, responder use different keys Draw challenges from different sets Make protocol resistant to attacks involving second parallel session CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011
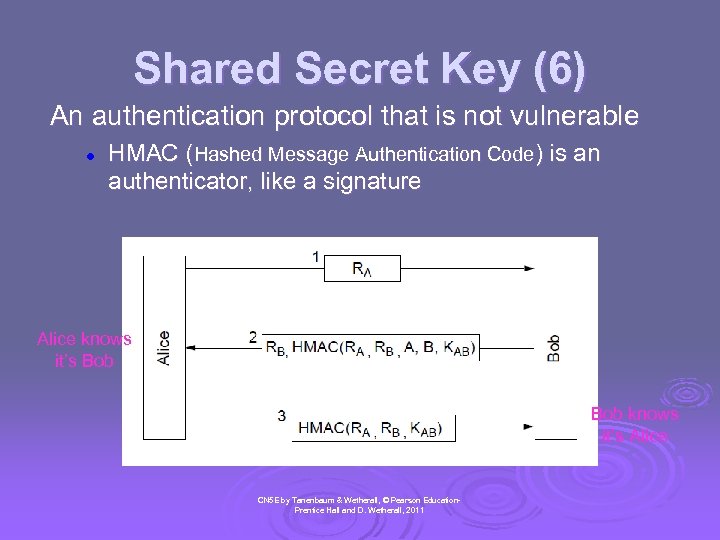
Shared Secret Key (6) An authentication protocol that is not vulnerable l HMAC (Hashed Message Authentication Code) is an authenticator, like a signature Alice knows it’s Bob knows it’s Alice CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011
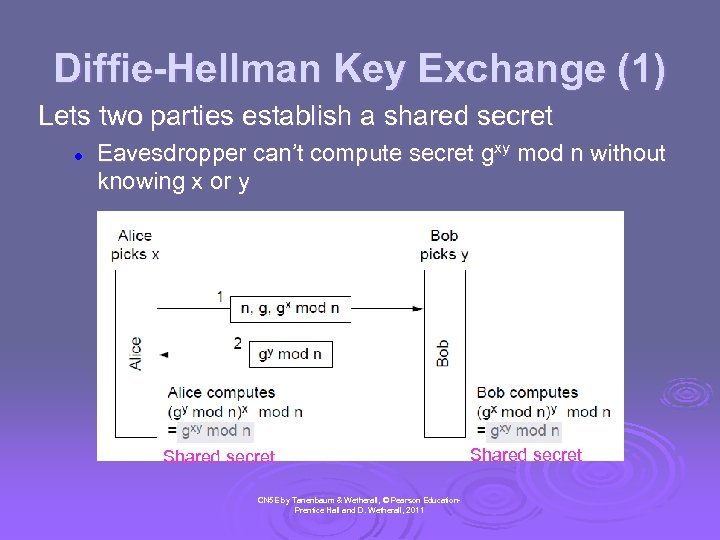
Diffie-Hellman Key Exchange (1) Lets two parties establish a shared secret l Eavesdropper can’t compute secret gxy mod n without knowing x or y Shared secret CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011 Shared secret

Diffie-Hellman Key Exchange (2) But it is vulnerable to a man-in-the-middle attack l Need to confirm identities, not just share a secret gxz mod n gzy mod n CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011 gzy mod n
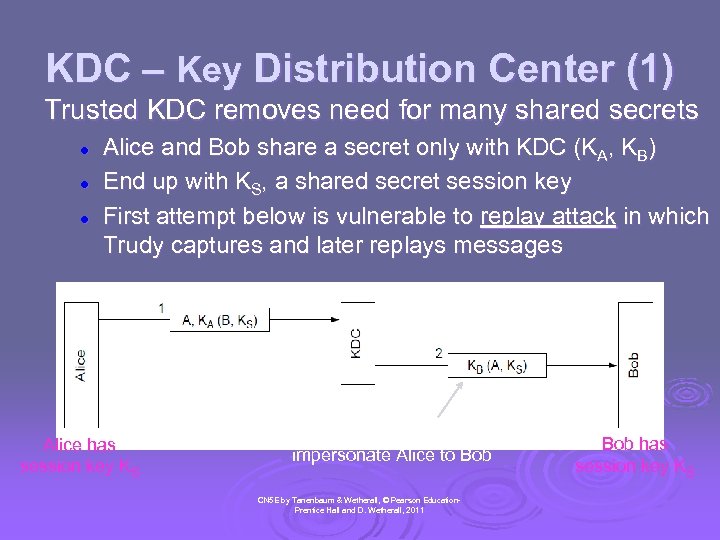
KDC – Key Distribution Center (1) Trusted KDC removes need for many shared secrets l l l Alice and Bob share a secret only with KDC (KA, KB) End up with KS, a shared secret session key First attempt below is vulnerable to replay attack in which Trudy captures and later replays messages Alice has session key KS Trudy can send this later to impersonate Alice to Bob CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011 Bob has session key KS
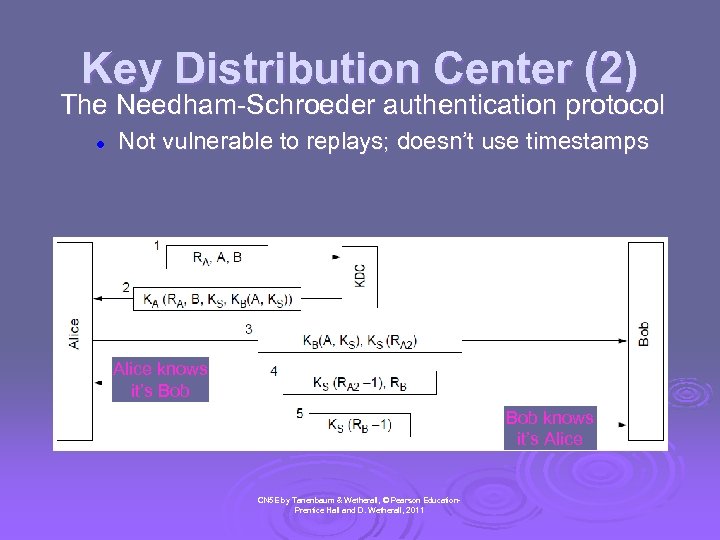
Key Distribution Center (2) The Needham-Schroeder authentication protocol l Not vulnerable to replays; doesn’t use timestamps Alice knows it’s Bob knows it’s Alice CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011
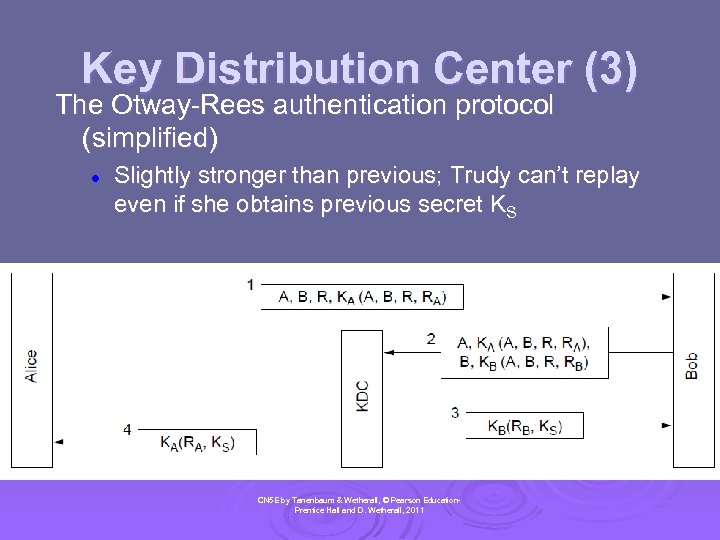
Key Distribution Center (3) The Otway-Rees authentication protocol (simplified) l Slightly stronger than previous; Trudy can’t replay even if she obtains previous secret KS CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011
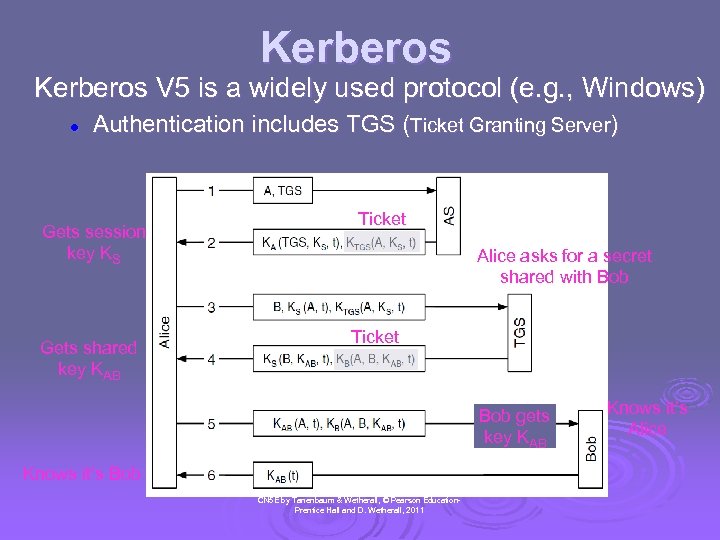
Kerberos V 5 is a widely used protocol (e. g. , Windows) l Authentication includes TGS (Ticket Granting Server) Gets session key KS Gets shared key KAB Ticket Alice asks for a secret shared with Bob Ticket Bob gets key KAB Knows it’s Bob CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011 Knows it’s Alice
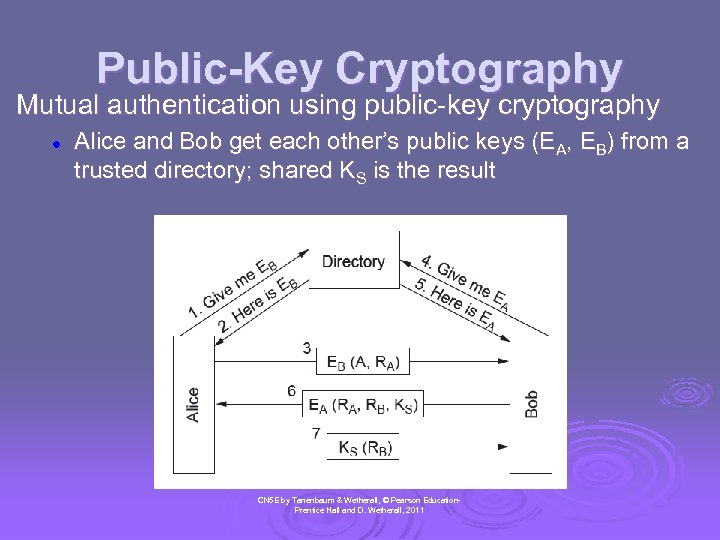
Public-Key Cryptography Mutual authentication using public-key cryptography l Alice and Bob get each other’s public keys (EA, EB) from a trusted directory; shared KS is the result CN 5 E by Tanenbaum & Wetherall, © Pearson Education. Prentice Hall and D. Wetherall, 2011
9d9ad0ec6320c8e080c82268e3fdbea0.ppt