496f30f284a02b8aa43026581f6dae77.ppt
- Количество слайдов: 19

Network Creation Game A. Fabrikant, A. Luthra, E. Maneva, C. H. Papadimitriou, and S. Shenker, PODC 2003 (Part of the Slides are taken from Alex Fabrikant’s presentation) 1

Context U C B E n n R K E L E Y C O M P U T E R S C I E N C E The internet has over 20, 000 Autonomous Systems (AS) Every AS picks their own peers to speed -up routing or minimize cost 2

Question: What is the performance penalty in terms of the poor network structure resulting from selfish users creating the network, without centralized control?

Goal of the paper U C B E R K n n n E L E Y C O M P U T E R S C I E N C E Introduces a simple model of network creation by selfish agents Briefly reviews game-theoretic concepts Computes the price of anarchy for different cost functions 4

A Simple Model for constructing G U C B E R n n n K E L E Y C O M P U T E R S C I E N C E N agents, each represented by a vertex and can buy (undirected) links to a set of others (si) One agent buys a link, but anyone can use it Cost to agent: Distance from i to j Pay $ for each link you buy Pay $1 for every hop to every node 5
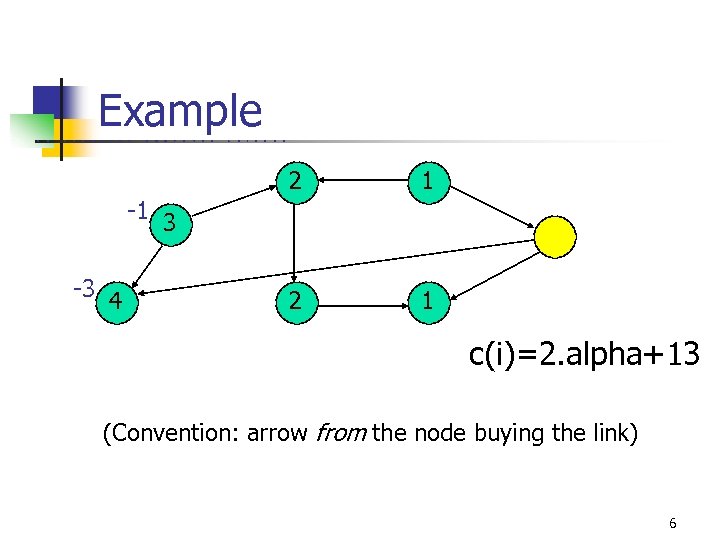
Example U C B E R K E L E Y C O M P U T E R S C I E N C E 2 1 -1 3 -3 4 c(i)=2. alpha+13 (Convention: arrow from the node buying the link) 6

Definitions U n n C B E R K E L E Y C O M P U T E R S C I E N C E V={1. . n} set of players A strategy for v is a set of vertices Sv= V{v}, such that v creates an edge to every w in Sv. G(S)=(V, E) is the resulting graph given a combination of strategies S=(S 1, . . , Sn), V set of players / nodes and E the laid edges. Social optimum: A central administrator’s approach to combining strategies and minimizing the total cost (social cost) It may not be liked by every node. Social cost: 7

Definitions: Nash Equilibria U C B E n R K E E Y C O M P U T E R S C I E N C E Nash equilibrium: a situation such that no single player can unilaterally modify its strategy and lower its cost n n n L Presumes complete rationality and knowledge on behalf of each agent Nash Equilibrium is not guaranteed to exist, but they do for our model The private cost of player i under s: 8

Definitions: Nash Equilibria U C B E n R K E L E Y C O M P U T E R S C I E N C E A combination of strategies S forms Nash equilibrium, if for any player i and every other strategy U (such that U differs from S only in i’s component) G(S) is the equilibrium graph. 9
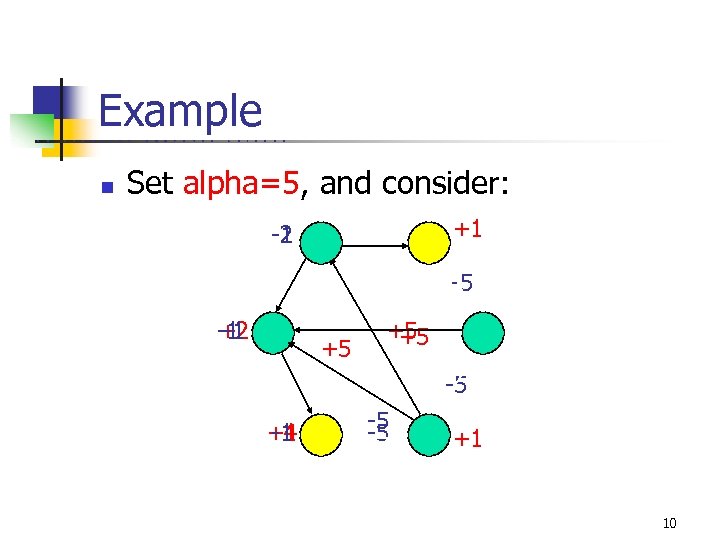
Example ? U C B E R K E L n E Y C O M P U T E R S C I E N C E Set alpha=5, and consider: +1 -1 -2 -5 -1 +2 -1 +5 +5 +5 -5 +4 +1 -1 -5 -5 +1 10

Definitions: Price of Anarchy U C B E n n R K E L E Y C O M P U T E R S C I E N C E Price of Anarchy (Koutsoupias & Papadimitriou, 1999): the ratio between the worst-case social cost of a Nash equilibrium network and the optimum social cost over all Nash equilibria. We bound the worst-case price of anarchy to limit “the price we pay” for operating without centralized control 11
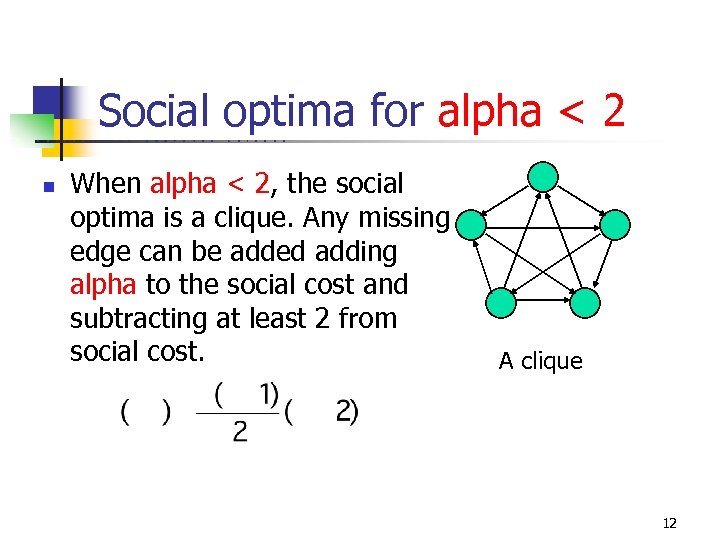
Social optima for alpha < 2 U C n B E R K E L E Y C O M P U T E R S C I E N C E When alpha < 2, the social optima is a clique. Any missing edge can be added adding alpha to the social cost and subtracting at least 2 from social cost. A clique 12

Nash Equilibrium for 1<alpha<2 U C B E R K E L E Y C O M P U T E R S C I E N C E When 1<alpha<2, the worstcase equilibrium configuration is a star. The total cost here is (n-1). (alpha + 2 n – 2) In a Nash Equilibrium, no single node can unilaterally add or delete an edge to bring down its cost. 13

Social optima for alpha > 2 U C B E n R K E L E Y C O M P U T E R S C I E N C E When alpha > 2, the social optima is a star. Any extra edges are too expensive. 14

Complexity issues U C B E R K E L E Y C O M P U T E R S C I E N C E Theorem. Computing the best response of a given peer is NP-hard. Proof hint. When 1 < alpha < 2, for a given node k, if there are no incoming edges, then the problem can be reduced to the Dominating Set problem. 15

Equilibria: very small U C B E R K E L n n E Y C O M P U T E R S C I E N C (<2) E For alpha<1, the clique is the only N. E. For 1<alpha<2, clique no longer N. E. , but the diameter is at most 2 -2 +alpha n Then, the star is the worst N. E. , can be seen to yield P. o. A. of at most 4/3 16

P. O. A for very small U C B E R K E L E Y C O M P U T E R S C I E N C (<2) E The star is also a Nash equilibrium, but there may be worse Nash equilibrium. 17

P. O. A for very small U C B E R K E L E Y C O M P U T E R S C I E N C (<2) E Proof. 18

The case of alpha > n 2 U C B E R K E L E Y C O M P U T E R S C I E N C E The Nash equilibrium is a tree, and the price of anarchy is 1. Why? 19
496f30f284a02b8aa43026581f6dae77.ppt