Нестандартные задачи как средство формирования математической компетенции в

Нестандартные задачи как средство формирования математической компетенции в начальной школе Глаголева Ю. И. , к. п. н. , доцент кафедры начального образования СПб АППО

• Являются средством формирования математической компетенции, таких качеств математического мышления, как гибкость, критичность, логичность, рациональность, органическое сочетание которых проявляется в особых способностях человека, дающих ему возможность успешно осуществлять творческую деятельность. • Нестандартные задачи вносят эмоциональный момент в умственную работу, позволяют рассматривать ситуацию их решения как проблемную, что способствует развитию внутренней мотивации, активизирующей психические процессы (память, внимание, мышление) • Для решения нестандартных задач учащимся необходимо приложить определенные усилия, проявить волю, настойчивость и целеустремленность. Необычность приемов решения прививает вкус к самостоятельным исследованиям, проявлению изобретательности, пробуждает положительные эмоции как в процессе решения задач, так и при достижении результата.

Виды нестандартных задач • арифметические текстовые задачи (задачи на предположение, на движение мимо объектов с учетом их протяженности, на движение в одном направлении; задачи, решаемые способом уравнивания или замены данных, методом инверсии (т. е. с «конца» ); задачи с неопределенными неизвестными); «сложные» задачи • комбинаторные задачи (на упорядочение предметов; на выбор подмножеств и их упорядочение; на определение количества различных вариантов; на выбор наилучшего результата по определенным критериям); • задачи на множества • логические задачи (на установление временных, пространственных, функциональных отношений; на активный перебор вариантов; на планирование деятельности; на установление сходства и отношения между элементами множеств; на оперирование категориями все, некоторые, отдельные); • ситуативные задачи • задачи на теорию вероятности

Этапы решения 1) анализ текста задачи (усвоение содержания), моделирование; 2) поиск решения (разбор задачи и составление плана решения); 3) осуществление плана решения; 4) проверка решения задачи. • Основные затруднения при решении задач данного вида возникают у учащихся прежде всего на начальных этапах хода решения, так как их попытки выбрать теоретический базис и способ действия, полагаясь на имеющийся субъектный опыт, в рассматриваемой ситуации не всегда успешны.

Нестандартные арифметические задачи (моделирование + рассуждения) • Тане с Сашей 14 лет, Саше с Петей 20 лет, а Тане с Петей 16 лет. Сколько лет Тане, Саше, Пете вместе. Сколько лет каждому их них?

Практический способ • В гараже 20 легковых и грузовых автомобилей, причем на каждую легковую машину приходится 4 грузовые. Сколько легковых и сколько грузовых машин в гараже • На стоянке у Мишиного дома было 8 транспортных средств: двухколесных мотоциклов и легковых автомобилей. Миша насчитал у них 22 колеса. Сколько мотоциклов и сколько автомобилей было на стоянке?

Метод исчерпывающих проб 1. Подумай, что обозначает каждое число в задаче. 2. Найди пары чисел, связанные между собой. 3. Составь из них выражения и объясни их смысл. 4. Из полученных выражений составь другие выражения и поясни их значение. 5. Из всех составленных выражений отбери нужные для решения задачи.

Доярки молочной фермы взяли обязательство за пастбищный сезон, продолжающийся 5 месяцев, получить от каждой коровы 3000 л молока. Выполнят ли они свое обязательство, если будут надаивать от каждой коровы по 20 л молока в день? (Считать, что в месяце 30 дней. ) 1) 3000 : 5 — молока нужно получить от каждой коровы за месяц; 2) 20 • 30 — всего молока получат за один месяц; 3) 30 • 5 — дней длится пастбищный сезон; 4) 3000 : 20 — дней потребуется фактически.

Логические задачи • Два мальчика играли в шашки 2 часа. Сколько играл каждый из них? • Масса петуха на двух ногах 4 кг. Какова будет масса, если петух встанет на 1 ногу. • В корзине лежат 5 яблок. Как разделить эти яблоки между пятью детьми, чтобы каждый получил по одному яблоку и одно яблоко осталось в корзине? • Миша, Сережа, Дима, Валера и Костя рисовали машины: – – – кто-то рисовал пожарную машину красным карандашом; кто-то гоночную машину синим фломастером; кто-то - грузовик коричневой ручкой; кто-то - легковую машину синим карандашом; кто-то - легковую машину коричневым фломастером. Миша и Сережа рисовали карандашом. Сережа и Дима рисовали одинаковым цветом. Кто что рисовал?

• Петя и Миша имеют фамилии Белов и Чернов. Какую фамилию имеет каждый из ребят, если Петя на два года старше Белова? • Ребята прыгали в длину. Дима прыгнул дальше Пети, а Сергей ближе Пети. Андрей прыгнул ближе Сергея, но дальше Юры. Коля прыгнул дальше Димы, а Боря так же, как Петя. Кто прыгнул ближе: Юра или Боря? Боря или Дима? (графический способ)

• Человек должен был перевезти в лодке через реку волка, козу и капусту. В лодке мог поместиться один человек, а с ним или волк, или коза, или капуста. Но наедине волк съест козу, коза капусту. Как человек это сделал?

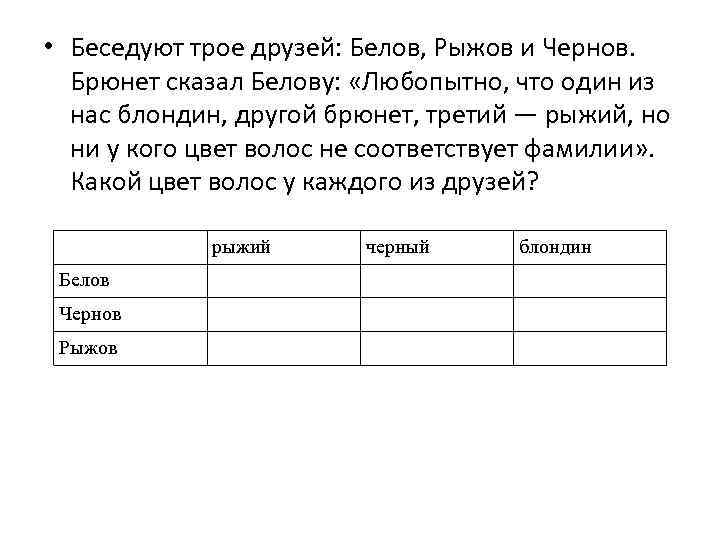• Беседуют трое друзей: Белов, Рыжов и Чернов. Брюнет сказал Белову: «Любопытно, что один из нас блондин, другой брюнет, третий — рыжий, но ни у кого цвет волос не соответствует фамилии» . Какой цвет волос у каждого из друзей? рыжий черный Белов Чернов Рыжов блондин

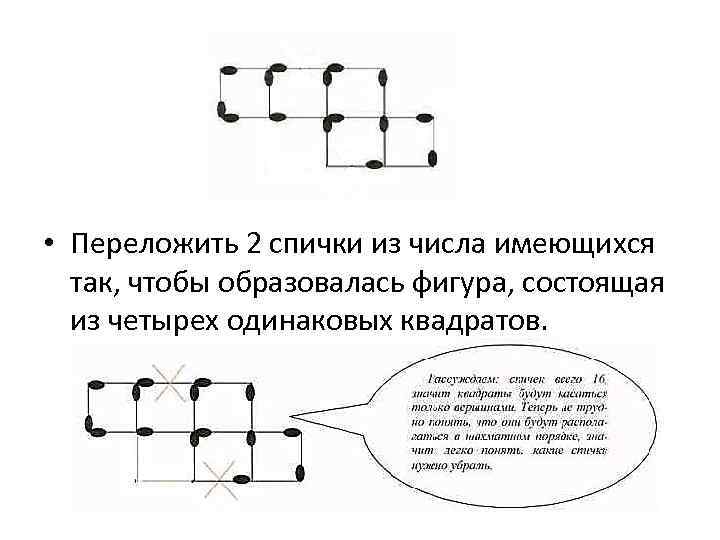• Переложить 2 спички из числа имеющихся так, чтобы образовалась фигура, состоящая из четырех одинаковых квадратов.

Комбинаторные задачи • Задачи выбора и расположения элементов некоторого множества в соответствии с заданными правилами Основной вопрос: Сколькими способами…? + магические квадраты, расшифровка, кодирование • Методы решения комбинаторных задач: – Формальные (определить характер выборки, выбрать соответствующую формулу, подставить число, вычислить = количество вариантов) – Неформальные (на первом плане сам процесс составления вариантов. Главное – какие варианты могут получиться. Метод перебора (хаотический, систематический), графические способы. )

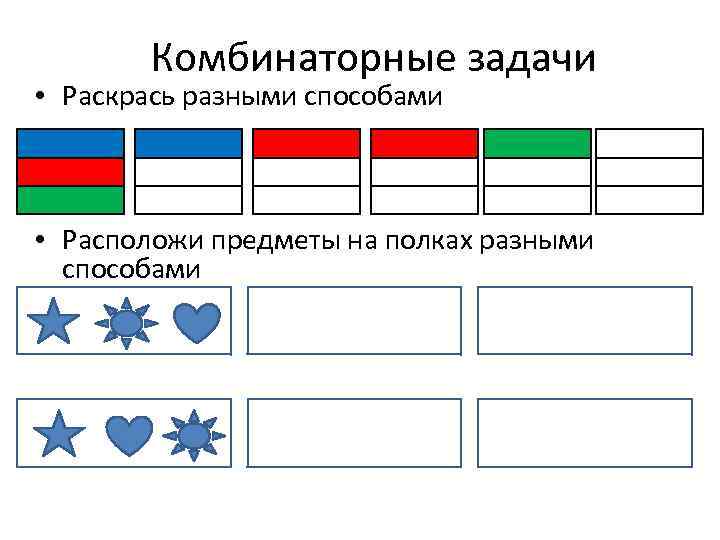Комбинаторные задачи • Раскрась разными способами • Расположи предметы на полках разными способами

• Составь все возможные трехзначные числа из цифр 2, 8, 3 так, чтобы цифры в записи числа не повторялись

• Сколько двузначных чисел можно записать лишь с помощью цифр 1, 2, 3, 4?

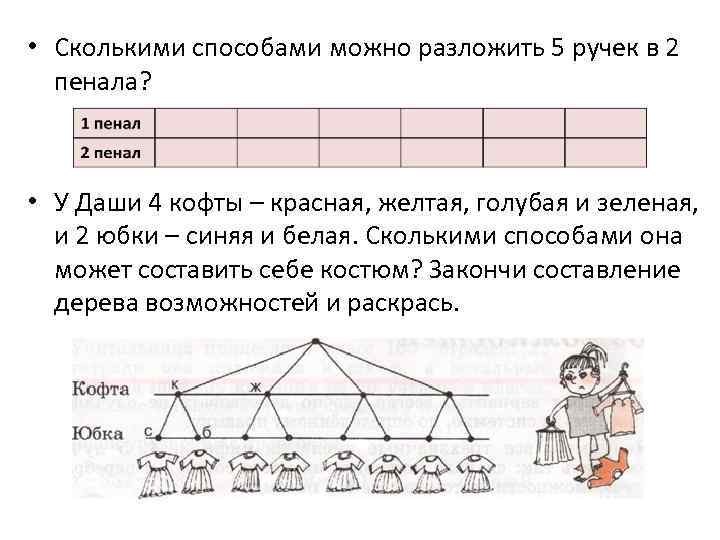• Сколькими способами можно разложить 5 ручек в 2 пенала? • У Даши 4 кофты – красная, желтая, голубая и зеленая, и 2 юбки – синяя и белая. Сколькими способами она может составить себе костюм? Закончи составление дерева возможностей и раскрась.

Графический способ • У каждой из трех сестер по одному брату. Сколько детей в семье • Пять человек обменялись рукопожатиями. Сколько было рукопожатий?

• Таня нашла 2 боровика, 2 подберезовика и 2 подосиновика и разложила их в 3 ряда так, чтобы в каждом было по одному грибу каждого вида. Как она это сделала?

• Как поставить 2 стула у четырех стен комнаты, чтобы у каждой стены стояло по одному стулу? • Как поставить 3 стула у четырех стен комнаты, чтобы у каждой стены стояло по одному стулу? • Как поставить 4 стула у четырех стен комнаты, чтобы у каждой стены стояло по два стула? • Как поставить 7 стульев у четырех стен комнаты, чтобы у каждой стены их было поровну?

Задачи на множества • • • Множество и его элементы Способы задания множеств Равные множества. Пустое множество Подмножество Разбиение множества на части по свойствам (классификация)* Пересечение множеств Свойства пересечения множеств* Объединение множеств. Свойства объединения множеств* Сложение и вычитание множеств*

Задачи на множества • Как называется множество овец? • Как называется множество лошадей? • Как называется множество пчел, летящих вместе? • Как называется множество футболистов, собравшихся вместе для игры? • Как называется множество кораблей, плывущих вместе?

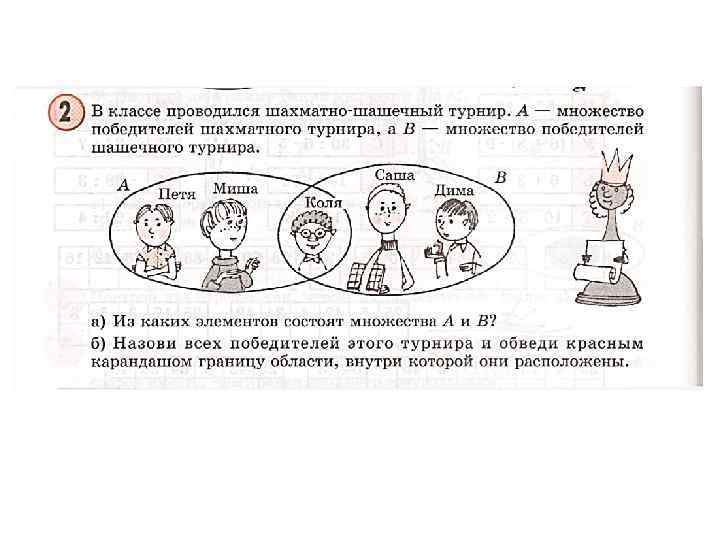
• Пришли 3 футболиста и 3 хоккеиста, а всего 5 человек. Может ли так быть? • В классе 25 учеников уже прочитали повесть о малыше и Карлсоне, а 23 ученика – повесть о Винни–Пухе, причем 18 человек прочитали обе повести. Сколько человек в классе, если каждый ученик прочитал хотя бы одну из этих книг?

• В классе 32 ученика. Из них 18 человек изучают английский язык, 16 человек – французский язык, причем все учащиеся изучают хотя бы один из двух иностранных языков. Сколько учащихся изучают одновременно английский и французский язык? Сколько изучают только английский язык? Только французский язык?