Нестандартные способы решения задач на смеси и сплавы

Нестандартные способы решения задач на смеси и сплавы Автор: Немченко Марина Германовна, учитель математики МАОУ лицея № 6 г. Тамбова

Задания из вариантов ЕГЭ 1. В сосуд, содержащий 5 литров 12% водного 5. Первый сплав содержит 10% меди, второй — 40% раствора некоторого вещества, добавили 7 литров меди. Масса второго сплава больше массы первого воды. Сколько процентов составляет на 3 кг. Из этих двух сплавов получили третий сплав, концентрация получившегося раствора? содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах. 2. Смешали некоторое количество 15% раствора некоторого вещества с таким же количеством 19% 6. Смешав 30% и 60% растворы кислоты и добавив раствора этого вещества. Сколько процентов 10 кг чистой воды, получили 36% раствор кислоты. составляет концентрация получившегося Если бы вместо 10 кг воды добавили 10 кг 50% раствора? раствора той же кислоты, то получили бы 41% раствор кислоты. Сколько килограммов 30% 3. Смешали 4 литра 15% водного раствора использовали для получения смеси? некоторого вещества с 6 литрами 25% водного раствора этого же вещества. Сколько процентов 7. Имеются два сосуда. Первый содержит 30 кг, а составляет концентрация получившегося второй — 20 кг раствора кислоты различной раствора? концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если 4. Имеется два сплава. Первый содержит 10% же смешать равные массы этих растворов, то никеля, второй — 30% никеля. Из этих двух получится раствор, содержащий 70% кислоты. сплавов получили третий сплав массой 200 кг, Сколько килограммов кислоты содержится в первом содержащий 25% никеля. На сколько килограммов сосуде? масса первого сплава меньше массы второго?

Задания из вступительных экзаменов в МГУ ХИМИЧЕСКИЙ ФАКУЛЬТЕТ МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ Имеются три металлических слитка. Первый весит 5 кг, второй – 3 кг, и каждый из этих двух слитков содержит 30% меди. Если первый слиток сплавить с третьим, то получится слиток, содержащий 56% меди, а если второй слиток сплавить с третьим, то получится слиток, содержащий 60% меди. Найти вес третьего слитка и процент содержания меди в нём. Сосуд вместимостью 8 л наполнен смесью кислорода и азота. На долю кислорода приходится 16% вместимости сосуда. Из сосуда выпускают некоторое количество смеси и впускают такое же количество азота, после чего опять выпускают такое же, как в первый раз, количество смеси и опять добавляют столько же азота. В новой смеси кислорода оказалось 9%. Какое количество смеси каждый раз выпускалось из сосуда?

Теоретическая часть

Теоретические основы Теоретические решения задач «на смеси, сплавы» решения задач Примем некоторые допущения: Все получающиеся сплавы или смеси однородны. При решении этих задач считается, что масса смеси нескольких веществ равна сумме масс компонентов. Определение. Процентным содержанием ( концентрацией) вещества в смеси называется отношение его массы к общей массе всей смеси. Это отношение может быть выражено либо в дробях, либо в процентах. Терминология: - процентное содержание вещества; - концентрация вещества; - массовая доля вещества. Всё это синонимы.

Практическая часть

Задача 1. Имеется два сплава меди и олова. Один сплав содержит 72% меди, а другой 80% меди. Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди?

Задача 1. Имеется два сплава меди и олова. Один сплав содержит 72% меди, а другой 80% меди. Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди? + =

Задача 1. Имеется два сплава меди и олова. Один сплав содержит 72% меди, а другой 80% меди. Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди? = + оло во медь = медь

Задача 1. Имеется два сплава меди и олова. Один сплав содержит 72% меди, а другой 80% меди. Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди? = + оло во медь 72% + медь = оло во медь + оло сви во нец оло во медь 80% = 75%

Задача 1. Имеется два сплава меди и олова. Один сплав содержит 72% меди, а другой 80% меди. Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди? = + оло во медь 72% оло во + 72% Хг + медь 80% оло во медь = оло во медь + оло во = оло во медь 80% (800 -Х) г 75% = медь 75% 800 г

Задача 1. Имеется два сплава меди и олова. Один сплав содержит 72% меди, а другой 80% меди. Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди? оло во медь 72% + Хг Решение: 1) Ответ: 500 г, 300 г. оло во медь 80% (800 -Х) г = медь 75% 800 г

Задача 1. Имеется два сплава меди и олова. Один сплав содержит 72% меди, а другой 80% меди. Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди? оло во медь 15% + Хг Решение: Ответ: 500 г, 300 г. медь 65% Уг оло во = медь 30% 200 г

Задача 1. Имеется два сплава меди и олова. Один сплав содержит 72% меди, а другой 80% меди. Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди? СТАРИННЫЙ СПОСОБ РЕШЕНИЯ 72 75 80 72 5 80 3 75 (800 : (5 + 3) = 100 г приходится на одну часть) для получения 800 г 75%-ного сплава нужно взять: 72%-ного сплава 100· 5 = 500 г, а 80%-ного – 100· 3 = 300 г. Ответ: 500 г, 300 г.

Задача 2. В каких пропорциях нужно сплавить золото 375 -й пробы с золотом 750 -й пробы, чтобы получить золото 500 -й пробы? СТАРИННЫЙ СПОСОБ РЕШЕНИЯ 375 250 750 125 500

Теоретическая часть

Правило креста или квадрат Пирсона Пусть требуется приготовить раствор определенной концентрации. В распоряжении имеется два раствора с более высокой и менее высокой концентрацией, чем нужно. Если обозначить массу первого раствора через m 1, а второго – через m 2, то при смешивании общая масса смеси будет складываться из суммы этих масс. Пусть массовая доля растворённого вещества в первом растворе – ω 1, во втором – ω 2, а в их смеси – ω 3. Тогда общая масса растворённого вещества в смеси будет складываться из масс растворённого вещества в исходных растворах: m 1 ω 1 + m 2 ω 2 = ω 3(m 1 + m 2), m 1(ω 1 – ω 3) = m 2(ω 3 – ω 2), Очевидно, что отношение массы первого раствора к массе второго раствора есть отношение разности массовых долей растворённого вещества в смеси и во втором растворе к разности соответствующих величин в первом растворе и в смеси.

При решении задач на растворы с разными концентрациями чаще всего применяют диагональную схему правила смешения или квадрат Пирсона. При расчётах записывают одну над другой массовые доли растворённого вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение. Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора. ω1 ω2 ω3 ω3 — ω2 ω1 — ω3

Практическая часть

Задача 3. Морская вода содержит 5% соли (по массе). Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составила 1, 5%? Решение: 5% 1, 5% 30 кг 3, 5% х кг 1, 5% 0%

Задача 4. Из сосуда, доверху наполненного 97% раствором кислоты, отлили 2 литра жидкости и долили 2 литра 45% раствора этой же кислоты. После этого в сосуде получился 81% раствор кислоты. Сколько литров раствора вмещает сосуд? Решение: 36% 97% (х-2) л 16% 2 л 81% 45%

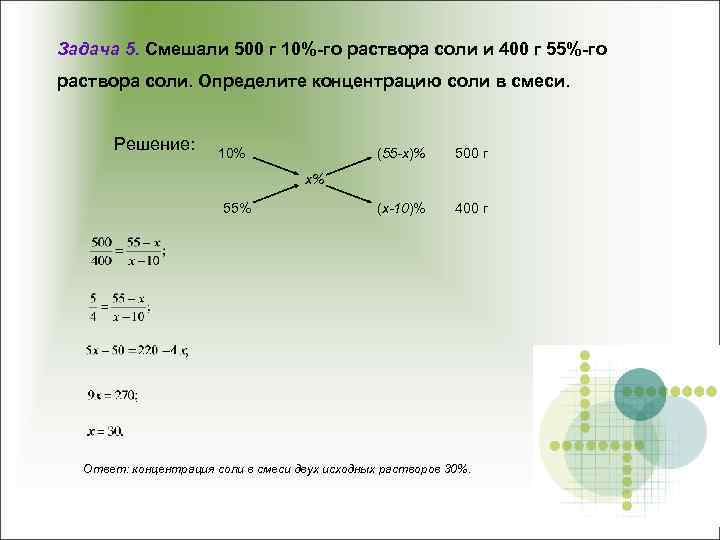
Задача 5. Смешали 500 г 10%-го раствора соли и 400 г 55%-го раствора соли. Определите концентрацию соли в смеси. Решение: 10% (55 -х)% 500 г (х-10)% 400 г х% 55% Ответ: концентрация соли в смеси двух исходных растворов 30%.

Задача 6. Имеются два слитка, содержащие медь. Масса второго слитка на 3 кг больше, чем масса первого слитка. Процентное содержание меди в первом слитке – 10%, во втором – 40%. После сплавления этих двух слитков, получился слиток, процентное содержание меди в котором 30%. Определить массу полученного слитка. Решение: 20% 40% (х+3) кг 30% 10% х кг

Задача 7. Сплавили 300 г сплава олова и меди, содержащего 60% олова, и 900 г сплава олова и меди, содержащего 80% олова. Сколько процентов олова в получившемся сплаве? Решение: 60% (80 -х)% 300 г (х-60)% 900 г х% 80%

Задача 8. В сосуд, содержащий 5 литров 12 -процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора? Решение: х% 12% 5 л (12–х)% 7 л х% 0% Ответ: 5%.

Задача 9. Смешали некоторое количество 15 -процентного раствора некоторого вещества с таким же количеством 19 -процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора? Решение: (19–х)% т г 15% х% 19% Ответ: 17%. (х– 15)% т г

Задача 10. Смешали 4 литра 15 -процентного водного раствора некоторого вещества с 6 литрами 25 -процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора? Решение: 15% (25–х)% 4 л (х– 15)% 6 л х% 25% Ответ: 21%.

Задача 11. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго? Решение: 5% 10% х кг 15% (200–х) кг 25% 30% 1) (кг) – 1 -й сплав; 2) (кг) – 2 -й сплав; 3) (кг) – разница. Ответ: на 100 кг.

Задача 12. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах. 10% х кг 20% (х+3) кг 30% Решение: 40% 1) (кг) — 1 -й сплав; 2) (кг) — 2 -й сплав; 3) (кг) — 3 -й сплав. Ответ: 9 кг.

Задача 13. По дороге ТУДА Винни Пух нашел дупло с мёдом. По его ощущениям этот мёд, к сожалению, только лишь на одну пятую часть правильный (остальные четыре пятые – неправильные). В дупле же, найденном по дороге ОБРАТНО, мёд на 60% правильный. Сколько килограммов мёда нужно взять из первого и второго(10 – Х) кг дупла, чтобы в общей сложности получить 10 кг меда, содержащего 32% правильного? Решение: Ответ: 7 килограммов из первого и 3 килограмма из второго дупла.

БЛАГОДАРЮ ЗА ВНИМАНИЕ