Несобственные интегралы 2

Несобственные интегралы

2

Несобственные интегралы с бесконечными пределами интегрирования Пусть функция y = f(x) определена и интегрируема на произвольном [a, b] функция определена для произвольного t a. 3

Определение. Несобственным интегралом от функции f(x) на полуинтервале [a, + ) называется предел функции F(t) при t стремящимся к + : Если предел, стоящий в правой части равенства, существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся. 4

При работе с несобственными интегралами выделяют следующие две задачи: 5

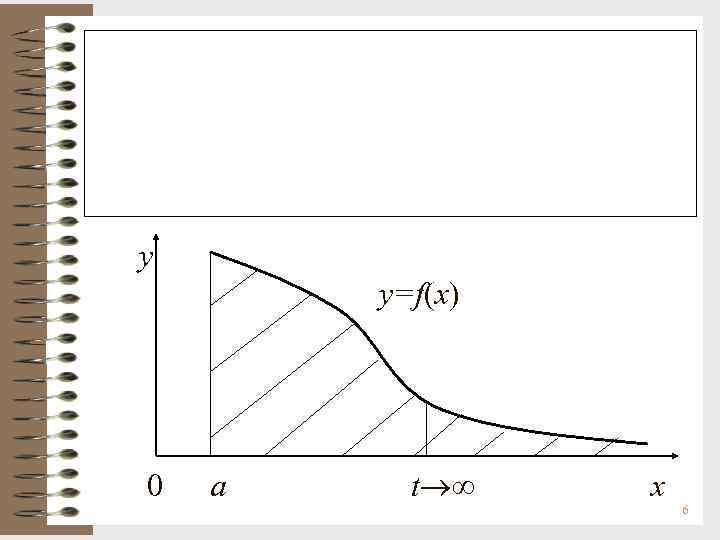
y y=f(x) 0 a t x 6

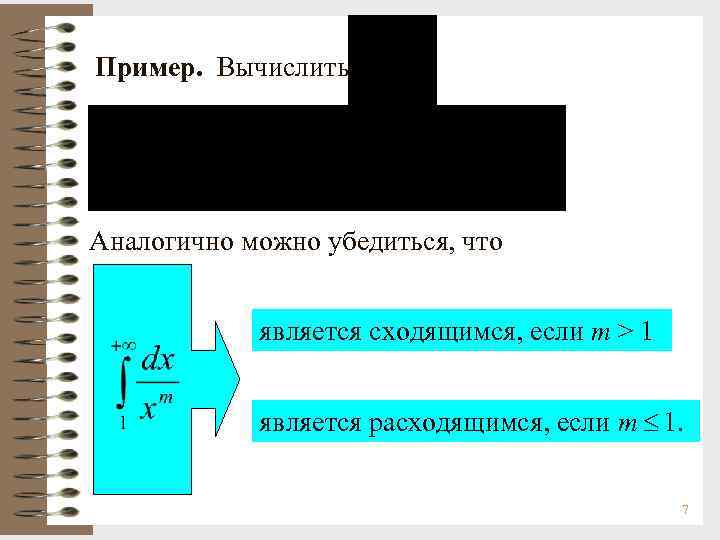
Пример. Вычислить Аналогично можно убедиться, что является сходящимся, если m > 1 является расходящимся, если m 1. 7

y y=1/xm (m<1) 1 y=1/x 0 1 x S=1/(m-1) 8

Определение сходимости интеграла аналогично. Введем понятие несобственного интеграла на ( - , + ). Пусть для некоторого числа а несобственные интегралы сходятся. Тогда положим, что 9

При этом интеграл называется сходящимся. Если хотя бы один из интегралов в правой части расходится, то несобственный интеграл называется расходящимся. 10

Пример. Вычислить Исследуем на сходимость интегралы и Таким образом, рассмотренный интеграл – расходится. 11

В курсе теории вероятностей встречается несобственный интеграл Эйлера- Пуассона: т. е. площадь S под кривой Гаусса на интервале (- , + ) равна 1. 12

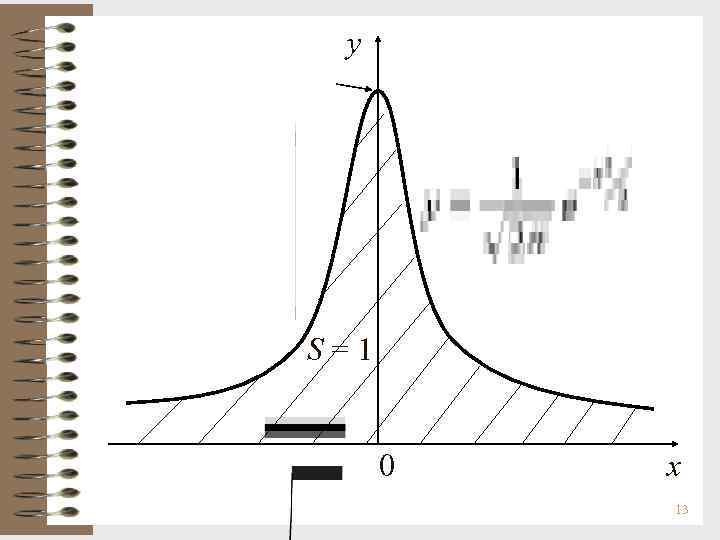
y S=1 0 x 13

Несобственные интегралы от неограниченных функций Пусть y = f(x) непрерывна, но не ограничена на полуинтервале [a, b). Определение. Если существует и конечен предел где > 0, то он называется несобственным интегралом от функции y = f(x) на [a, b). 14

Пример. Вычислить Полубесконечная фигура, ограниченная осями координат, кривой и прямой х = 1, имеет конечную площадь S = 2 кв. ед. 16

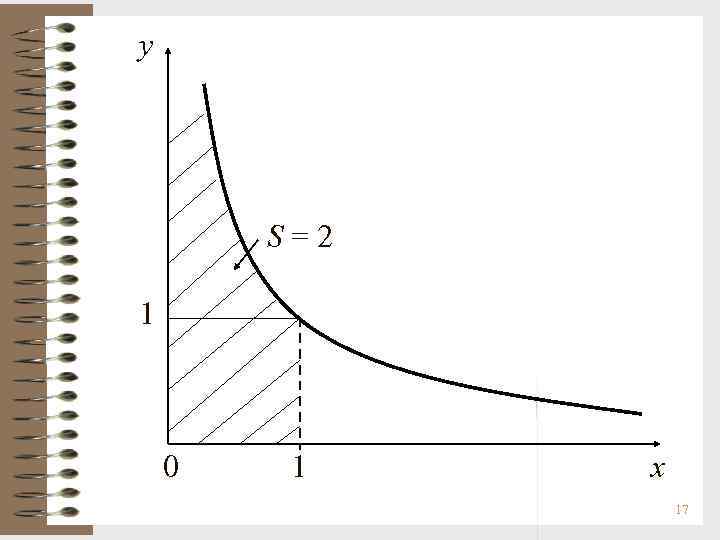
y S=2 1 0 1 x 17