Непрерывные сообщения.

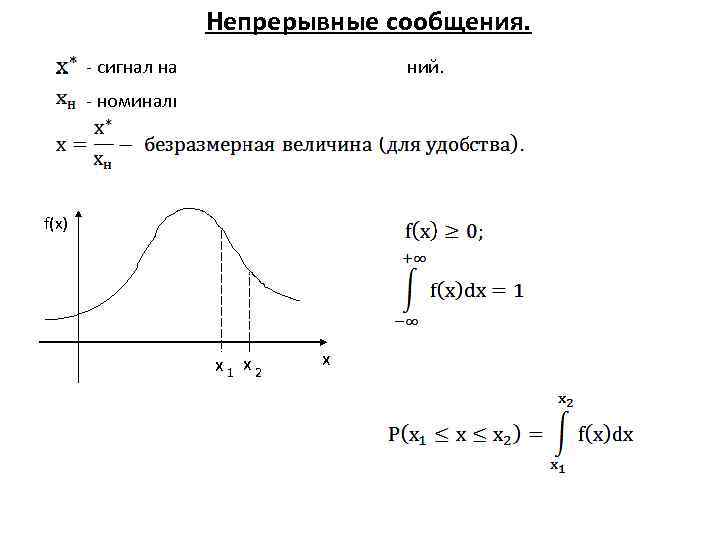
Непрерывные сообщения. - сигнал на выходе источника сообщений. - номинальные значения сигнала. f(x) х1 х2 х

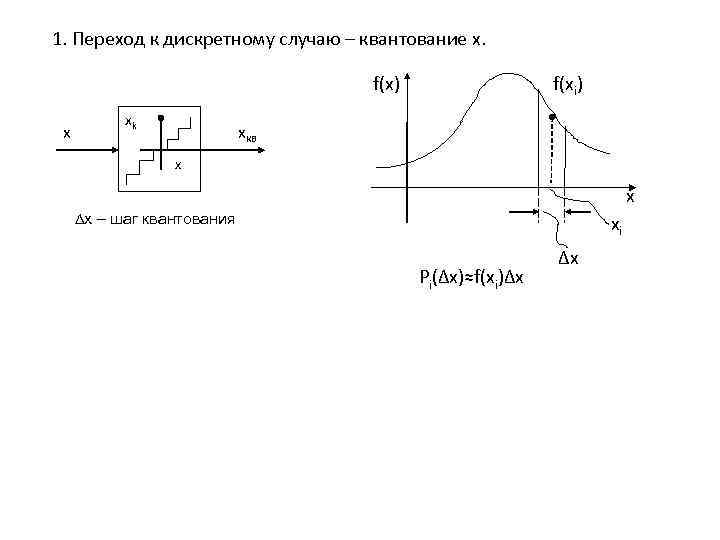
1. Переход к дискретному случаю – квантование x. f(x) f(xi) xk x xкв x x ∆x – шаг квантования xi ∆x Pi(∆x)≈f(xi)∆x

1. Энтропия источника сообщений после квантования. 1

3. Дифференциальная энтропия. f(x) a в Если в-а=1, то Дифференциальная энтропия: В дальнейшем можно опускать индекс “q”, понимая, что речь идёт о дифференциальной энтропии источника непрерывных сообщений.

Взаимная информация fx(xi) fy(y) fx(x) fy(yi) ∆x x ∆y y xi yi Дано: Воспоминания: Если x и y статистически не связаны, то Если x и y однозначно связаны:

1. Квантуем по уровню x с шагом ∆x; 2. Квантуем по уровню y с шагом ∆y; 3. 4. Для дискретных (квантованных) сообщений: При ∆x→ 0 и ∆y→ 0 выражение остаются теми же.

Средняя взаимная информация.

Максимум дифференциальной энтропии. Задача 1. Определить максимум при заданном диапазоне случайной величины X: а≤x≤в. Таким образом: а≤x≤в; Воспоминания: y(x)-неизвестная функция.

Условие Требуется найти y(x), доставляющую максимум (минимум) J. Уравнение Эйлера:

Решение:

Задача 2. Определить максимум дифференциальной энтропии при заданной мощности (дисперсии) сигнала. Определить максимум при условии: Обратите внимание: диапазон не ограничен (1); математическое ожидание принято равным 0 (2).

Решение: а в

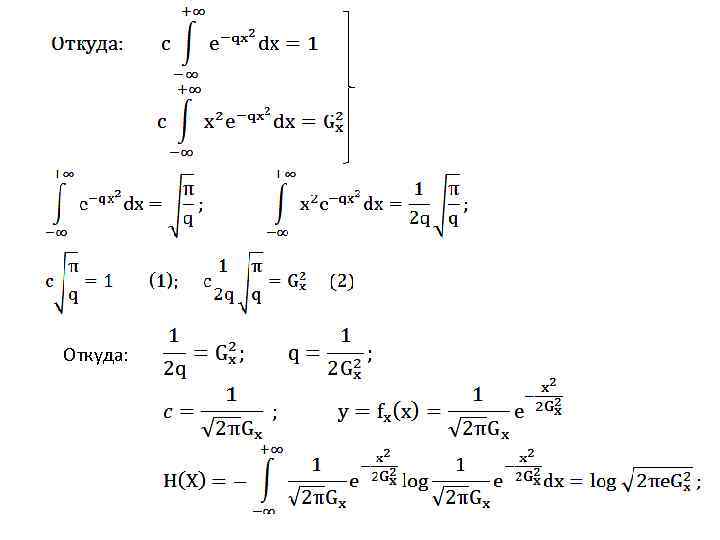
Откуда:

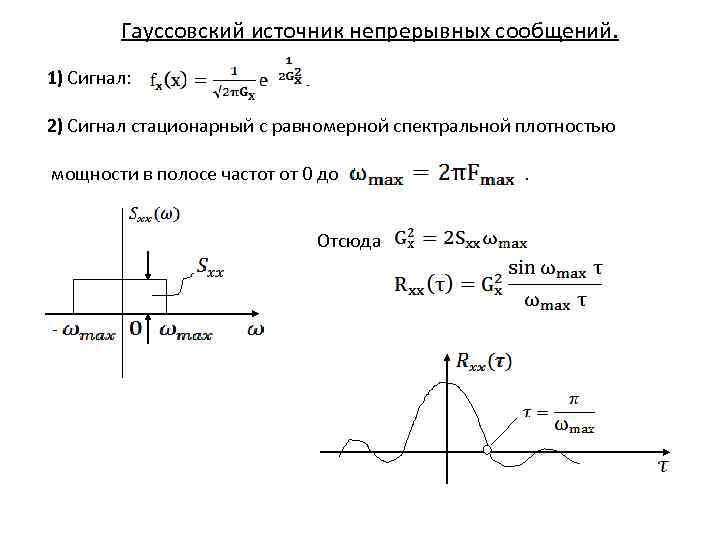
Гауссовский источник непрерывных сообщений. 1) Сигнал: 2) Сигнал стационарный с равномерной спектральной плотностью мощности в полосе частот от 0 до . Отсюда -

3) В соответствии с теоремой Котельникова передаём информацию с шагом временной дискретизации. Эти отсчеты не коррелированны (а так как сигнал гауссовский, то и независимы). Некоррелированность следует из Отсюда источник отсчетов без памяти. 4) Производительность гауссовского источника при фиксированном Δx (этим учитываем факт использования дифференциальной энтропии) равна: Пропускная способность гауссовского канала связи (формула Шеннона-Таллера).

Гауссовский канал: 1. Источник сообщений гауссовский: закон распределения амплитуд синала гауссов, сигнал стационарный с постоянной плотностью мощности в полосе частот от 0 до 2. Помеха в(t) – аддитивная, имеет гауссовский закон распределения: y(t)=x(t)+в(t) сигнал на входе приемника сигнал помеха 3. Помеха статистически не связана с сигналом: f(в|x)= f(x|в)=

4. Помеха имеет постоянную спектральную плотность мощности в полосе канала от 0 до Отсюда следует, что отсчеты помехи с шагом временной дискретизации статистически независимы.

Требуется определить С – пропускную способность гауссовского канала. При передачи отсчетов с шагом источник сообщений и канал связи «без памяти» . Отсюда определяется при гауссовом источнике, дающем максимум дифференциальной энтропии при заданной мощности, и введенной модели аддитивной помехи.

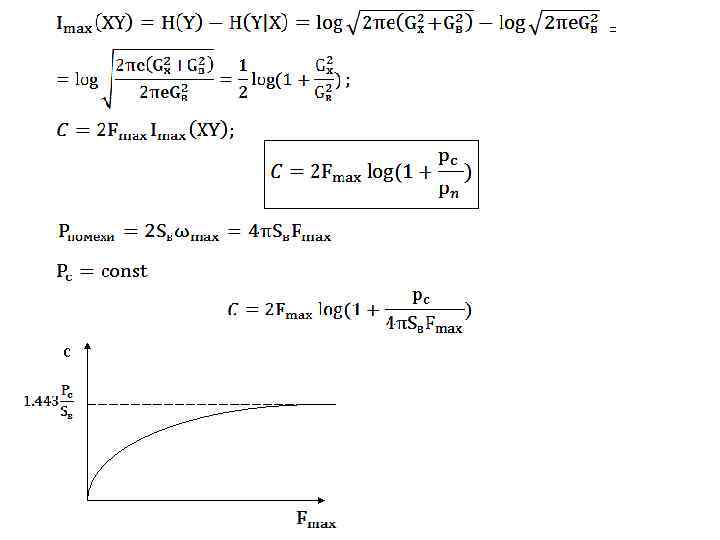
= с