Непараметрические тесты Тест Вилкоксона (сравнение двух парных выборок) Выдвигается гипотеза о равенстве значений (распределений) • Находится разность парных значений di. H 0: d = 0 H 1: d 0 • Новая выборка ранжируется по абсолютному значению разности (знак разности при этом не учитывается). • Каждому рангу приписывается знак разности di. • Находится сумма положительных рангов (T+) и сумма отрицательных рангов (T ). Если проверяемые методы одинаковы, то следует ожидать близких значений T+ и T. • Критическое значение находится по таблице из справочника и сравнивается с T. Гипотеза отвергается, если вычисленный критерий меньше критического значения.
U-тест Две группы измерений (они могут быть разного объема, n 1 и n 2 ) ранжируются как одна группа. Находится сумма рангов по первой (R 1) и по второй (R 2) группе. Затем вычисляются величины: H 0 : U 1 = U 2 H 1 : U 1 U 2 (U 1 + U 2 = n 1 n 2 ) Дальше находим критическое значение по таблице из справочника на заданном уровне значимости. Если вычисленный критерий меньше критического значения, то гипотеза отвергается.
Регрессия. Метод наименьших квадратов Предполагается, что (линейная модель) Остаток Оценка
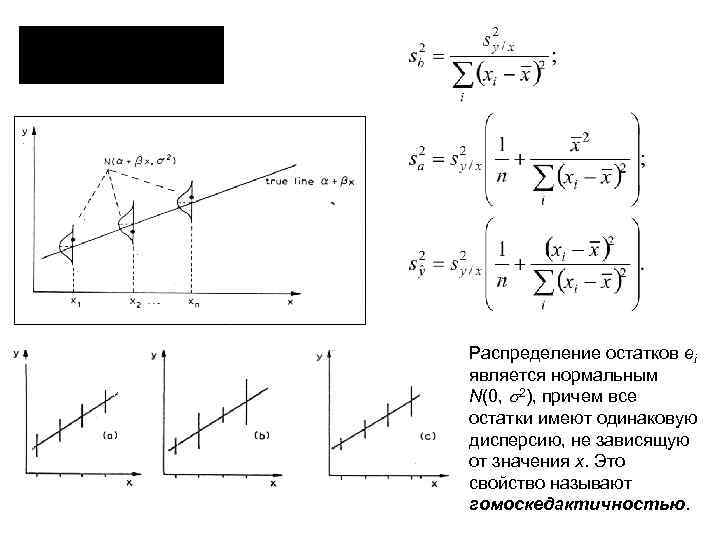
Распределение остатков ei является нормальным N(0, 2), причем все остатки имеют одинаковую дисперсию, не зависящую от значения x. Это свойство называют гомоскедактичностью.
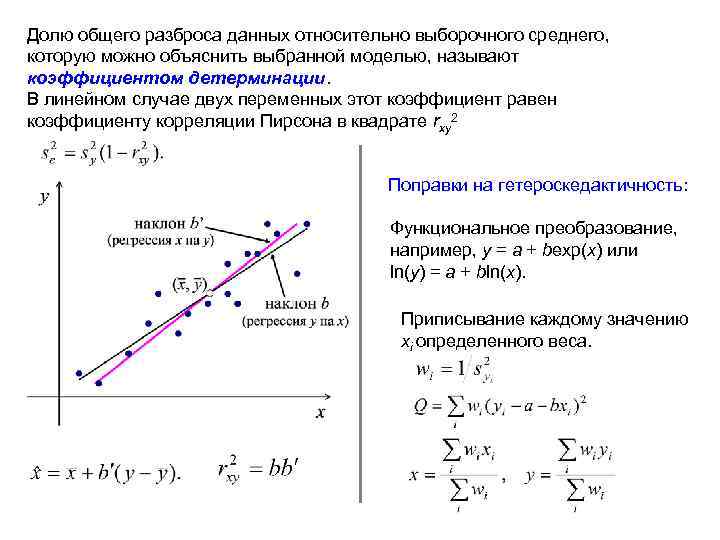
Долю общего разброса данных относительно выборочного среднего, которую можно объяснить выбранной моделью, называют коэффициентом детерминации. В линейном случае двух переменных этот коэффициент равен коэффициенту корреляции Пирсона в квадрате rxy 2 Поправки на гетероскедактичность: Функциональное преобразование, например, y = a + bexp(x) или ln(y) = a + bln(x). Приписывание каждому значению xi определенного веса.
Сравнение двух процедур для парных измерений с помощью регрессионного анализа В идеале при отсутствии ошибок результаты измерения нескольких образцов тестовой процедурой y и проверяемой (новой) процедурой x, должны ложиться на прямую y = x, наклон прямой = 1, а константа = 0. Оценка случайной ошибки: Проверка гипотез по t-тестам: = 1 (есть ли мультипликативная систематическая ошибка? ) число степеней свободы n – 2, r – коэффициент корреляции Пирсона = 0 (есть ли аддитивная систематическая ошибка? )
Скачать презентацию Непараметрические тесты Тест Вилкоксона сравнение двух парных выборок
Part4-2011.ppt