Непараметрические методы в медицине Статистические методы Параметрические

Непараметрические методы в медицине

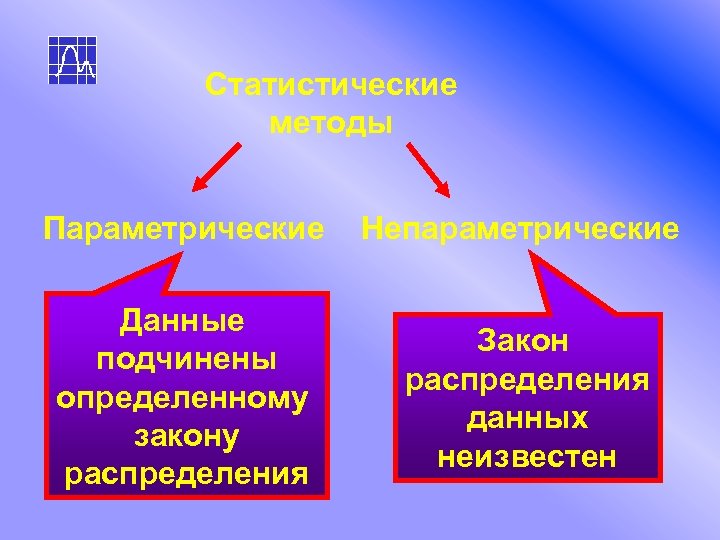Статистические методы Параметрические Непараметрические Данные подчинены определенному закону распределения Закон распределения данных неизвестен

Методы • Регрессионные модели • Факторное разложение • Дисперсионный анализ • Критерии однородности выборок

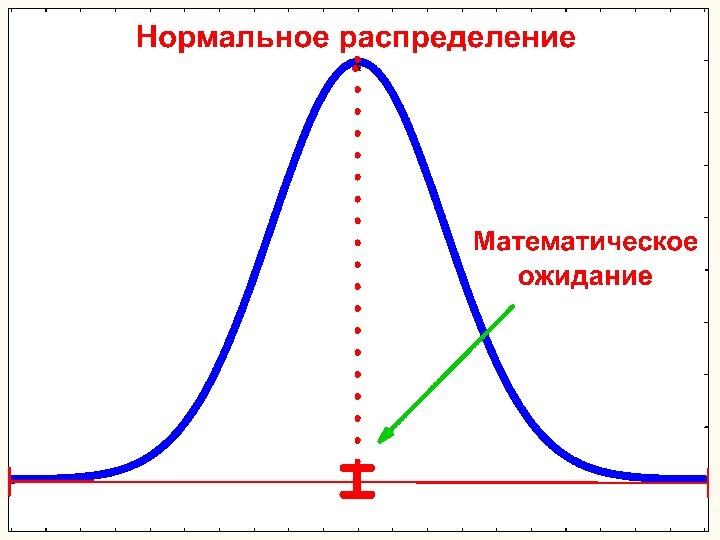
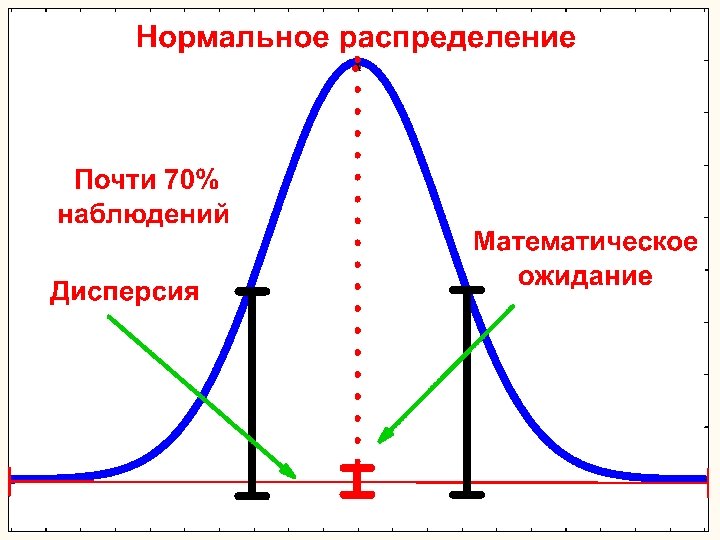
Параметрические методы Часто предполагают, что распределение исходных данных подчиняется нормальному закону

Критерий Стьюдента для независимых выборок Критерий Стьюдента для зависимых выборок Однофакторный дисперсионный анализ

Непараметрические методы

Проверка однородности двух независимых выборок ?

Параметрический метод решения данной задачи критерий Стьюдента Непараметрическим аналогом критерия Стьюдента является критерий Вальда-Вольфовица (критерий серий)

Критерий Вальда-Вольфовица (критерий серий) Данные: две независимые выборки

Критерий Вальда-Вольфовица Нулевая гипотеза: выборки принадлежат к одной и той же совокупности

Критерий Вальда-Вольфовица Шаг 1. Отсортировываем по возрастанию обобщенный ряд

Критерий Вальда-Вольфовица Шаг 2. В полученном ряде считаем число серий - последовательностей из элементов одной выборки

Критерий Вальда-Вольфовица В случае, если нулевая гипотеза верна, число и длина серий для каждой выборки - случайны. Если число и длина серий сильно различаются, то отвергаем нулевую гипотезу

Критерий Вальда-Вольфовица Пример: Проницаемость сосудов сетчатки Необходимо проверить, что при заболеваниях сетчатки повышается проницаемость ее сосудов

Критерий Вальда-Вольфовица Была измерена проницаемость сосудов сетчатки у 12 здоровых и у 12 больных с ее поражением

Критерий Вальда-Вольфовица Структура данных следующая: имеется две переменных независимая и зависимая. Зависимая переменная содержит все наблюдения для обеих выборок, независимая содержит коды-идентификаторы выборок

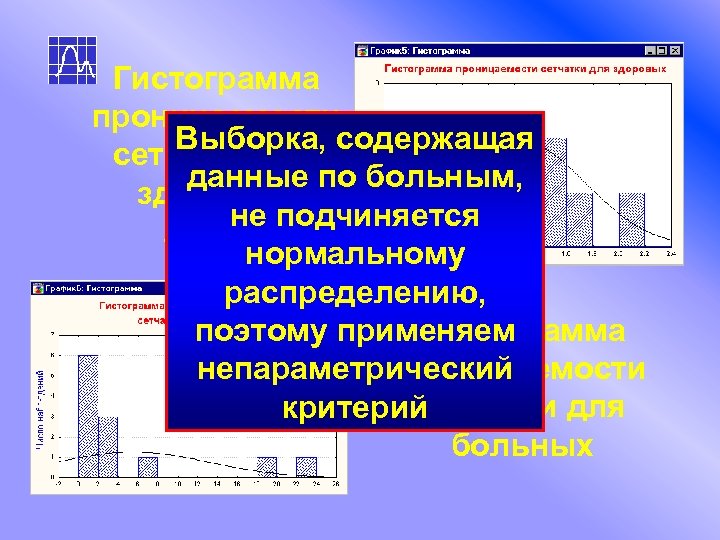Гистограмма проницаемости Выборка, содержащая сетчатки для данные по больным, здоровых не подчиняется людей нормальному распределению, Гистограмма поэтому применяем проницаемости непараметрический сетчатки для критерий больных

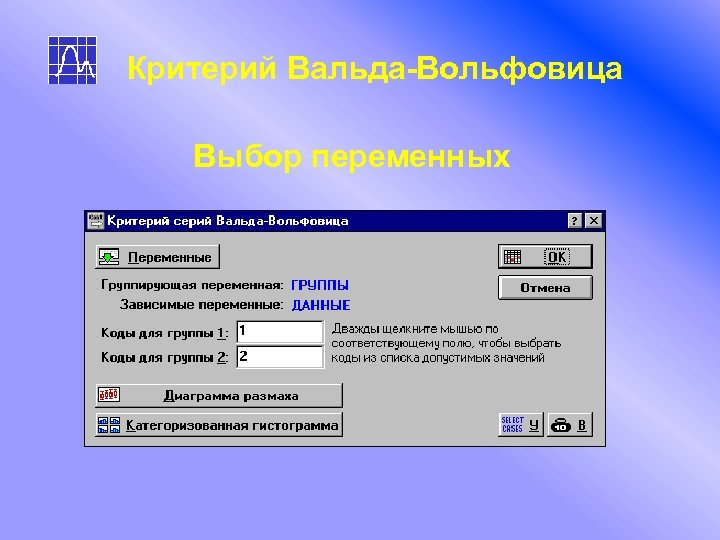Критерий Вальда-Вольфовица Выбор переменных

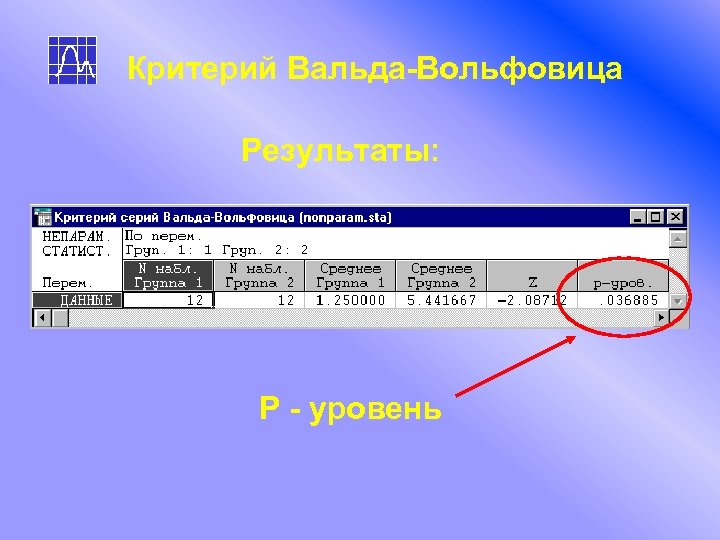Критерий Вальда-Вольфовица Результаты: P - уровень

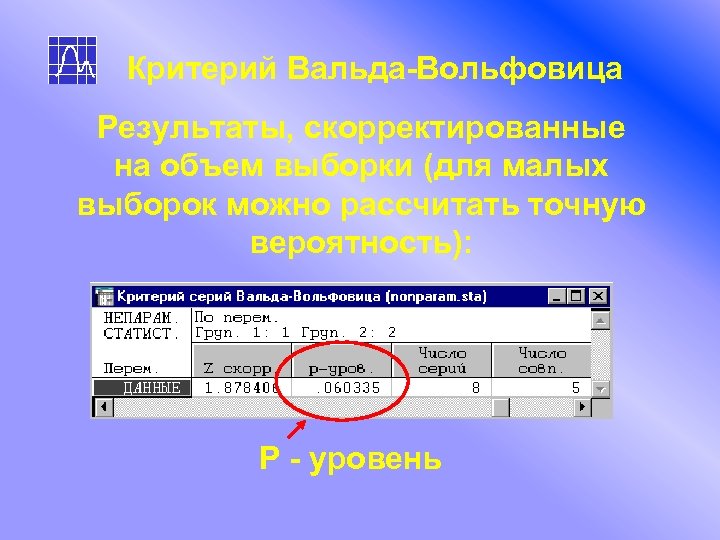Критерий Вальда-Вольфовица Результаты, скорректированные на объем выборки (для малых выборок можно рассчитать точную вероятность): P - уровень

Критерий Вальда-Вольфовица Значение P - уровня оказалось равным 0. 036, что позволяет отвергнуть нулевую гипотезу о сходстве в проницаемости сосудов сетчатки для здоровых и больных людей на 5% уровне значимости

Критерий Вальда-Вольфовица Вывод: При заболеваниях сетчатки повышается проницаемость ее сосудов

Парные наблюдения Пациенты наблюдаются ДО и ПОСЛЕ лечения

Парные наблюдения изучаются в анализе эффективности действия препарата или метода лечения

Критерий Уилкоксона Шаг 1. Находят разности между значениями ДО и значениями ПОСЛЕ Шаг 2. Составляют из них общий ряд и выстраивают по возрастанию абсолютной величины показателя

Критерий Уилкоксона Шаг 3. Отдельно вычисляют сумму рангов положительных и отрицательных разностей - T+ и TШаг 4. Меньшее из значений T+ и Tсравнивают с критическим

Критерий Уилкоксона В противном случае Если нулевая гипотеза верна, либо положительные то значения T+ и T-отрицательные либо не должны сильно различаться, разности накапливаются более того, общего ряда, в начале меньшая должна превышать что означает наличие критическое значение эффекта

Критерий Уилкоксона Пример: Курение и функции тромбоцитов

Критерий Уилкоксона Известно, что курение способствует ишемической болезни сердца

Критерий Уилкоксона Определенную роль в развитии этого заболевания играют тромбоциты Исследовался показатель агрегация тромбоцитов

Критерий Уилкоксона Ставился эксперимент по определению влияния курения на агрегацию тромбоцитов У 11 участников проведены измерения агрегации тромбоцитов ДО и ПОСЛЕ курения

Критерий Уилкоксона Для проведения этого критерия в STATISTICA структура данных должна быть следующей: В одной переменной содержатся агрегации тромбоцитов ДО курения, в другой - ПОСЛЕ курения

Критерий Уилкоксона Данные по агрегации тромбоцитов для 11 участников

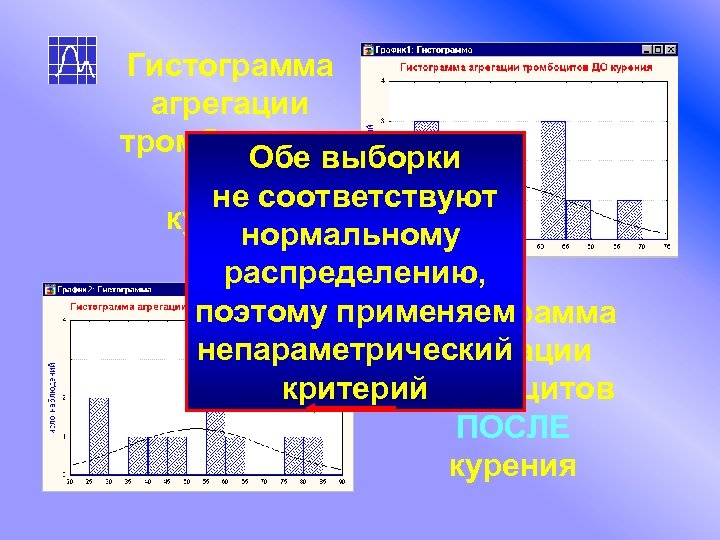Гистограмма агрегации тромбоцитов Обе выборки ДО соответствуют не курения нормальному распределению, поэтому применяем Гистограмма непараметрический агрегации критерий тромбоцитов ПОСЛЕ курения

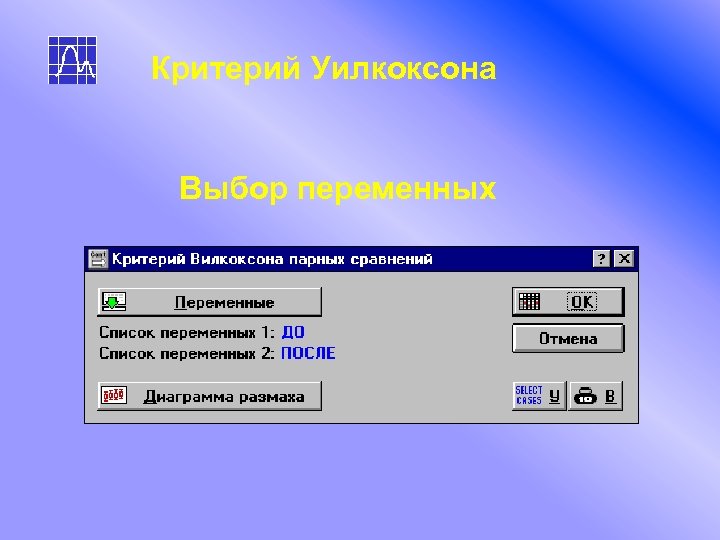Критерий Уилкоксона Выбор переменных

Критерий Уилкоксона Результаты критерия: Значение T-статистики P - уровень

Критерий Уилкоксона Значение p - уровня меньше 0. 01, следовательно, на уровня значимости 1% мы можем отвергнуть нулевую гипотезу об отсутствии зависимости Вывод: курение приводит к агрегации тромбоцитов

Сравнение влияния различных воздействий на одну группу пациентов или однородные группы Q - критерий Кохрейна

Q - критерий Кохрейна Данные о воздействии приводятся в альтернативной шкале “ 1” - было воздействие, “ 0” - не было воздействия

Q - критерий Кохрейна Нулевая гипотеза: доли всех изучаемых воздействий одинаковы Если доли сильно различаются, то эффективность воздействий разная

Q - критерий Кохрейна Пример: Исследование эффективности различных видов терапии

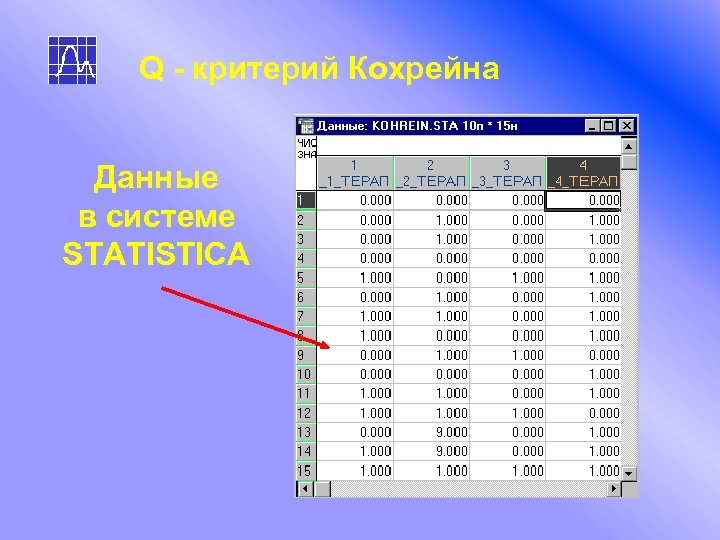Q - критерий Кохрейна Данные в системе STATISTICA

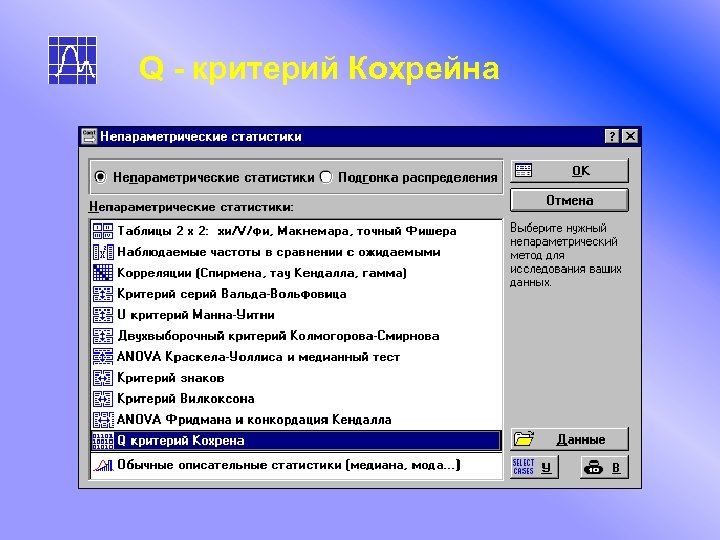Q - критерий Кохрейна

Q - критерий Кохрейна Выбор переменных: Коды, отличные от 0 и 1, временно перекодируются в 0 и 1.

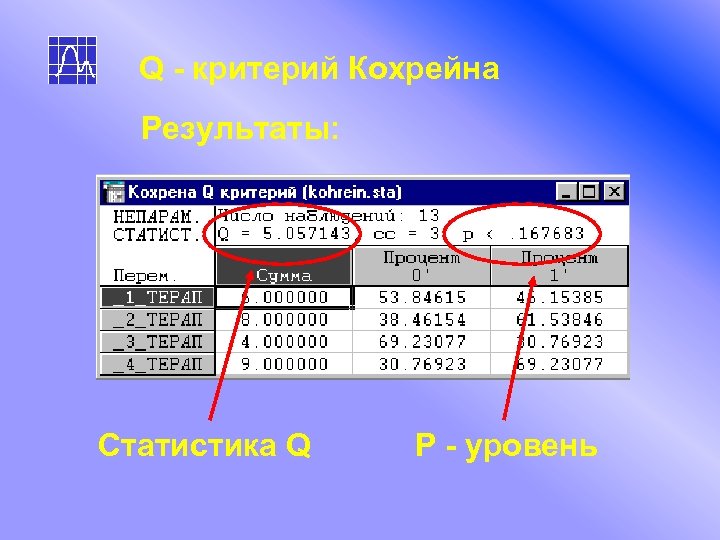Q - критерий Кохрейна Результаты: Статистика Q Р - уровень

Q - критерий Кохрейна Значение р - уровня получилось 0. 167, что больше критического значения 0. 05, следовательно, мы не можем отвергнуть нулевую гипотезу и делаем вывод: Ни одна из терапий по эффективности не отличается сильно от других

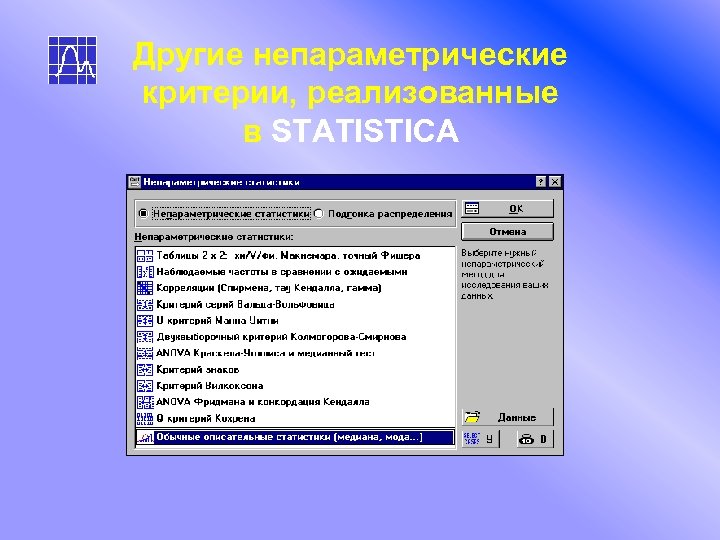Другие непараметрические критерии, реализованные в STATISTICA

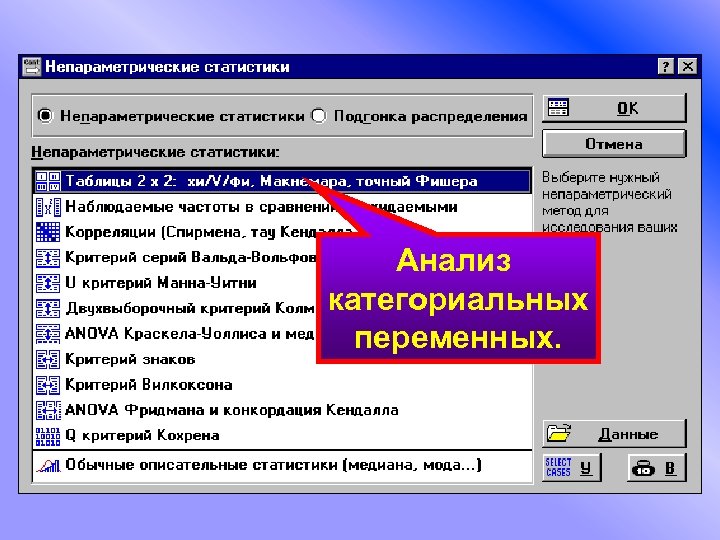Анализ категориальных переменных.

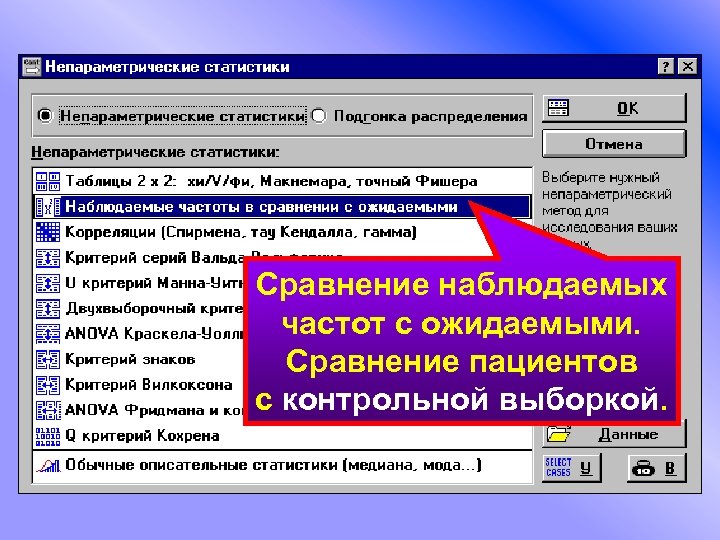Сравнение наблюдаемых частот с ожидаемыми. Сравнение пациентов с контрольной выборкой.

Ранговые корреляции. Поиск взаимосвязей ранжированных переменных.

Критерий однородности двух выборок, основанный на сравнении числа серий последовательностей из элементов одной выборки.

Критерий проверки принадлежности двух выборок к одной совокупности, основанный на сравнении общих свойств распределения.

Критерий проверки принадлежности нескольких выборок к одной совокупности. Анализ воздействия нескольких препаратов.

Непараметрическая альтернатива критерия Стьюдента для парных наблюдений. Сравнение состояния здоровья пациентов ДО и ПОСЛЕ лечения.

Критерий позволяет проверить наличие эффекта при проведении нескольких повторных экспериментов.

Пакет программ STATISTICA - современный подход к анализу данных с применением информационных технологий