Семинар 6. Непараметрические критерии.ppt
- Количество слайдов: 22
 Непараметрические критерии
Непараметрические критерии
 НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ Параметрические критерии предполагают, что генеральная совокупность подчиняется определенному закону распределения (чаще всего распределению Гаусса) Непараметрические критерии не опираются на дополнительные предположения о распределении изучаемой случайной величины Параметрические критерии неприменимы в ряде ситуаций: - вид распределения неизвестен или он заведомо отличается от нормального (t-критерий и др. методы неприменимы); - ограничен объем выборки (критерий хи-квадрат может быть неприменим); - данные представляют из себя неизмеряемые величины (ранги, порядковые номера, признаки, факторы и т. д. ).
НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ Параметрические критерии предполагают, что генеральная совокупность подчиняется определенному закону распределения (чаще всего распределению Гаусса) Непараметрические критерии не опираются на дополнительные предположения о распределении изучаемой случайной величины Параметрические критерии неприменимы в ряде ситуаций: - вид распределения неизвестен или он заведомо отличается от нормального (t-критерий и др. методы неприменимы); - ограничен объем выборки (критерий хи-квадрат может быть неприменим); - данные представляют из себя неизмеряемые величины (ранги, порядковые номера, признаки, факторы и т. д. ).
 Критерий Розенбаума А: В: 7 Применим для сравнения двух выборок, близких по объему 10 11 14 22 28 36 3 5 6 8 10 12 17 18 20 22 25 Q=3+4=7 Q 0. 05=6 40 48 49 52 39 Q 0. 01=9 Различия значимы при p<5%, но не значимы при p<1% Критерий очень прост, но его мощность невысока, т. е. он «увидит» только действительно сильное различие (m=11) (n=12)
Критерий Розенбаума А: В: 7 Применим для сравнения двух выборок, близких по объему 10 11 14 22 28 36 3 5 6 8 10 12 17 18 20 22 25 Q=3+4=7 Q 0. 05=6 40 48 49 52 39 Q 0. 01=9 Различия значимы при p<5%, но не значимы при p<1% Критерий очень прост, но его мощность невысока, т. е. он «увидит» только действительно сильное различие (m=11) (n=12)
 1. Ранговые критерии 3 выборка ранговые значения ранги 5 4 7 10 7 9 10 14 16 5 6 7 8 Xi : 3 4 5 i: 1 2 3 4 9 16 14 Критерии, в которых вместо выборочных значений используются их ранги, называются ранговыми критериями
1. Ранговые критерии 3 выборка ранговые значения ранги 5 4 7 10 7 9 10 14 16 5 6 7 8 Xi : 3 4 5 i: 1 2 3 4 9 16 14 Критерии, в которых вместо выборочных значений используются их ранги, называются ранговыми критериями
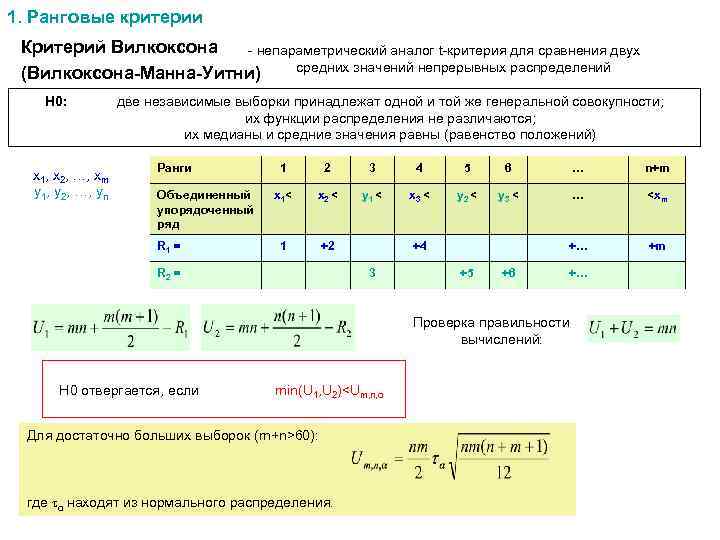 1. Ранговые критерии Критерий Вилкоксона - непараметрический аналог t-критерия для сравнения двух средних значений непрерывных распределений (Вилкоксона-Манна-Уитни) H 0: x 1, x 2, …, xm y 1, y 2, …, yn две независимые выборки принадлежат одной и той же генеральной совокупности; их функции распределения не различаются; их медианы и средние значения равны (равенство положений) Ранги Объединенный упорядоченный ряд R 1 = 1 2 3 4 5 6 … n+m x 1< x 2 < y 1 < x 3 < y 2 < y 3 < …
1. Ранговые критерии Критерий Вилкоксона - непараметрический аналог t-критерия для сравнения двух средних значений непрерывных распределений (Вилкоксона-Манна-Уитни) H 0: x 1, x 2, …, xm y 1, y 2, …, yn две независимые выборки принадлежат одной и той же генеральной совокупности; их функции распределения не различаются; их медианы и средние значения равны (равенство положений) Ранги Объединенный упорядоченный ряд R 1 = 1 2 3 4 5 6 … n+m x 1< x 2 < y 1 < x 3 < y 2 < y 3 < …
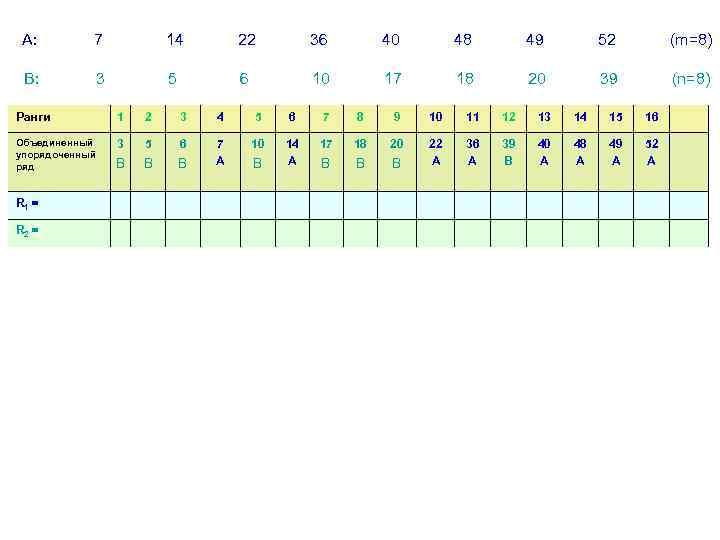 А: 7 14 22 36 40 48 49 52 (m=8) В: 3 5 6 10 17 18 20 39 (n=8) Ранги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Объединенный упорядоченный ряд 3 5 6 10 18 20 В В 14 А 17 В 7 А В В В 22 А 36 А 39 В 40 А 48 А 49 А 52 А R 1 = R 2 = В
А: 7 14 22 36 40 48 49 52 (m=8) В: 3 5 6 10 17 18 20 39 (n=8) Ранги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Объединенный упорядоченный ряд 3 5 6 10 18 20 В В 14 А 17 В 7 А В В В 22 А 36 А 39 В 40 А 48 А 49 А 52 А R 1 = R 2 = В
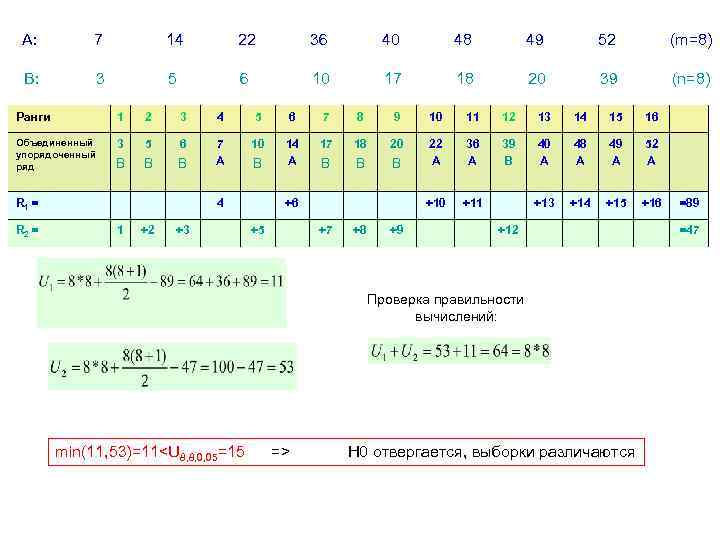 А: 7 14 22 36 40 48 49 52 (m=8) В: 3 5 6 10 17 18 20 39 (n=8) Ранги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Объединенный упорядоченный ряд 3 5 6 10 18 20 В В 14 А 17 В 7 А В В В 22 А 36 А 39 В 40 А 48 А 49 А 52 А +10 +11 +13 +14 +15 +16 R 1 = R 2 = В 4 1 +2 +3 +6 +5 +7 +8 +9 +12 Проверка правильности вычислений: min(11, 53)=11 H 0 отвергается, выборки различаются =89 =47
А: 7 14 22 36 40 48 49 52 (m=8) В: 3 5 6 10 17 18 20 39 (n=8) Ранги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Объединенный упорядоченный ряд 3 5 6 10 18 20 В В 14 А 17 В 7 А В В В 22 А 36 А 39 В 40 А 48 А 49 А 52 А +10 +11 +13 +14 +15 +16 R 1 = R 2 = В 4 1 +2 +3 +6 +5 +7 +8 +9 +12 Проверка правильности вычислений: min(11, 53)=11 H 0 отвергается, выборки различаются =89 =47
 Критерии согласия Критерий Колмогорова-Смирнова H 0: закон стат. распределения двух выборок не отличается, в том числе имеется равенство средних, дисперсий, асимметрий, эксцессов и др. характеристик непараметрический аналог χ2 критерия для сравнения распределений - при сравнении двух выборок - при сравнении эмпирического распределения с теоретическим H 0 отвергается, если D>Dmaxα
Критерии согласия Критерий Колмогорова-Смирнова H 0: закон стат. распределения двух выборок не отличается, в том числе имеется равенство средних, дисперсий, асимметрий, эксцессов и др. характеристик непараметрический аналог χ2 критерия для сравнения распределений - при сравнении двух выборок - при сравнении эмпирического распределения с теоретическим H 0 отвергается, если D>Dmaxα
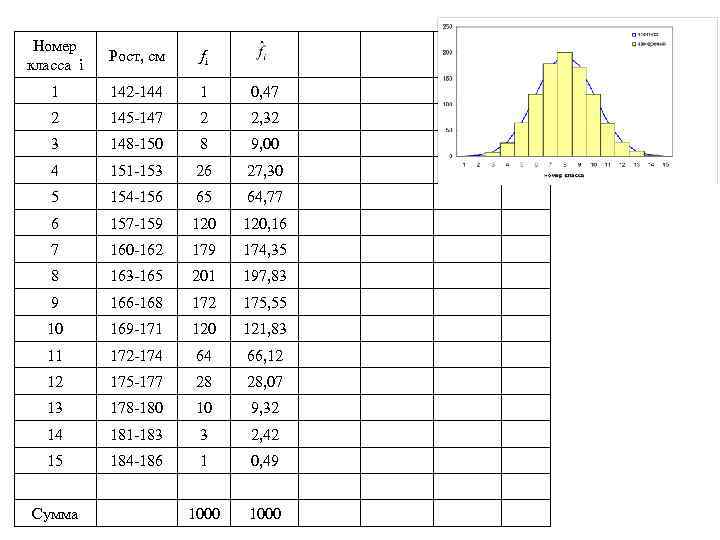 Номер класса i Рост, см fi 1 142 -144 1 0, 47 2 145 -147 2 2, 32 3 148 -150 8 9, 00 4 151 -153 26 27, 30 5 154 -156 65 64, 77 6 157 -159 120, 16 7 160 -162 179 174, 35 8 163 -165 201 197, 83 9 166 -168 172 175, 55 10 169 -171 120 121, 83 11 172 -174 64 66, 12 12 175 -177 28 28, 07 13 178 -180 10 9, 32 14 181 -183 3 2, 42 15 184 -186 1 0, 49 1000 Сумма
Номер класса i Рост, см fi 1 142 -144 1 0, 47 2 145 -147 2 2, 32 3 148 -150 8 9, 00 4 151 -153 26 27, 30 5 154 -156 65 64, 77 6 157 -159 120, 16 7 160 -162 179 174, 35 8 163 -165 201 197, 83 9 166 -168 172 175, 55 10 169 -171 120 121, 83 11 172 -174 64 66, 12 12 175 -177 28 28, 07 13 178 -180 10 9, 32 14 181 -183 3 2, 42 15 184 -186 1 0, 49 1000 Сумма
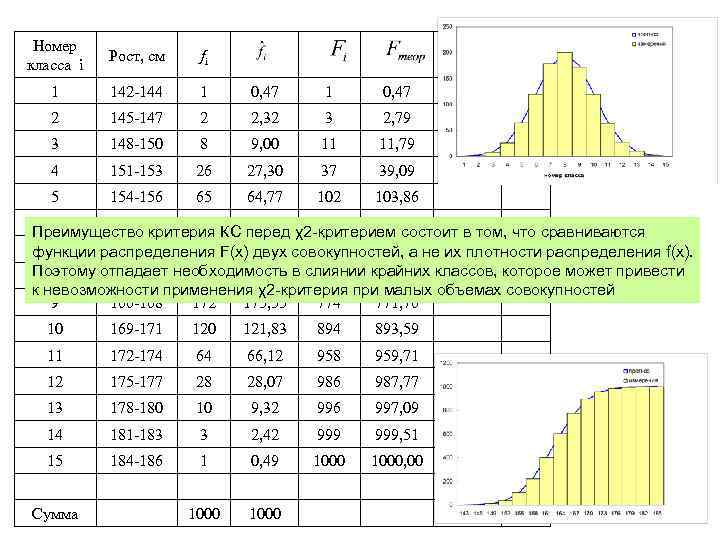 Номер класса i Рост, см fi 1 142 -144 1 0, 47 2 145 -147 2 2, 32 3 2, 79 3 148 -150 8 9, 00 11 11, 79 4 151 -153 26 27, 30 37 39, 09 5 154 -156 65 64, 77 102 103, 86 6 157 -159 120, 16 222 224, 03 Преимущество критерия КС перед χ2 -критерием состоит в том, что сравниваются 7 160 -162 179 174, 35 401 398, 38 функции распределения F(x) двух совокупностей, а не их плотности распределения f(x). Поэтому отпадает необходимость в слиянии крайних классов, которое может привести 8 163 -165 201 197, 83 602 596, 21 к невозможности применения χ2 -критерия при малых объемах совокупностей 9 166 -168 172 175, 55 774 771, 76 10 169 -171 120 121, 83 894 893, 59 11 172 -174 64 66, 12 958 959, 71 12 175 -177 28 28, 07 986 987, 77 13 178 -180 10 9, 32 996 997, 09 14 181 -183 3 2, 42 999, 51 15 184 -186 1 0, 49 1000, 00 1000 Сумма
Номер класса i Рост, см fi 1 142 -144 1 0, 47 2 145 -147 2 2, 32 3 2, 79 3 148 -150 8 9, 00 11 11, 79 4 151 -153 26 27, 30 37 39, 09 5 154 -156 65 64, 77 102 103, 86 6 157 -159 120, 16 222 224, 03 Преимущество критерия КС перед χ2 -критерием состоит в том, что сравниваются 7 160 -162 179 174, 35 401 398, 38 функции распределения F(x) двух совокупностей, а не их плотности распределения f(x). Поэтому отпадает необходимость в слиянии крайних классов, которое может привести 8 163 -165 201 197, 83 602 596, 21 к невозможности применения χ2 -критерия при малых объемах совокупностей 9 166 -168 172 175, 55 774 771, 76 10 169 -171 120 121, 83 894 893, 59 11 172 -174 64 66, 12 958 959, 71 12 175 -177 28 28, 07 986 987, 77 13 178 -180 10 9, 32 996 997, 09 14 181 -183 3 2, 42 999, 51 15 184 -186 1 0, 49 1000, 00 1000 Сумма
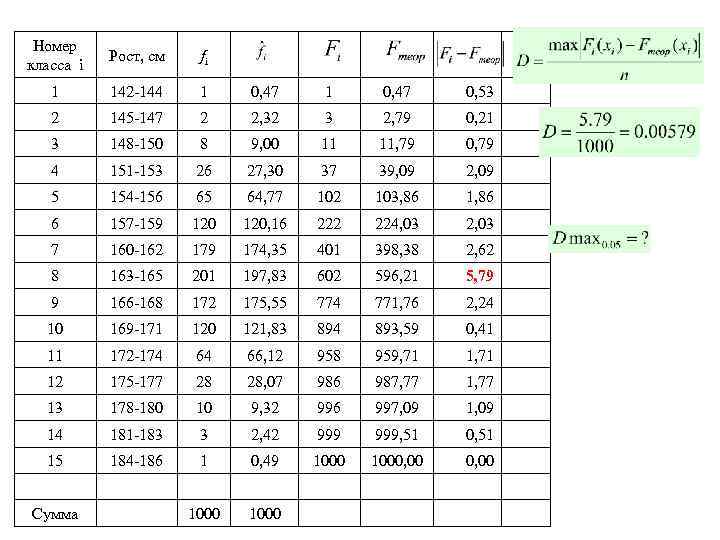 Номер класса i Рост, см fi 1 142 -144 1 0, 47 0, 53 2 145 -147 2 2, 32 3 2, 79 0, 21 3 148 -150 8 9, 00 11 11, 79 0, 79 4 151 -153 26 27, 30 37 39, 09 2, 09 5 154 -156 65 64, 77 102 103, 86 1, 86 6 157 -159 120, 16 222 224, 03 2, 03 7 160 -162 179 174, 35 401 398, 38 2, 62 8 163 -165 201 197, 83 602 596, 21 5, 79 9 166 -168 172 175, 55 774 771, 76 2, 24 10 169 -171 120 121, 83 894 893, 59 0, 41 11 172 -174 64 66, 12 958 959, 71 12 175 -177 28 28, 07 986 987, 77 13 178 -180 10 9, 32 996 997, 09 14 181 -183 3 2, 42 999, 51 0, 51 15 184 -186 1 0, 49 1000, 00 1000 Сумма
Номер класса i Рост, см fi 1 142 -144 1 0, 47 0, 53 2 145 -147 2 2, 32 3 2, 79 0, 21 3 148 -150 8 9, 00 11 11, 79 0, 79 4 151 -153 26 27, 30 37 39, 09 2, 09 5 154 -156 65 64, 77 102 103, 86 1, 86 6 157 -159 120, 16 222 224, 03 2, 03 7 160 -162 179 174, 35 401 398, 38 2, 62 8 163 -165 201 197, 83 602 596, 21 5, 79 9 166 -168 172 175, 55 774 771, 76 2, 24 10 169 -171 120 121, 83 894 893, 59 0, 41 11 172 -174 64 66, 12 958 959, 71 12 175 -177 28 28, 07 986 987, 77 13 178 -180 10 9, 32 996 997, 09 14 181 -183 3 2, 42 999, 51 0, 51 15 184 -186 1 0, 49 1000, 00 1000 Сумма
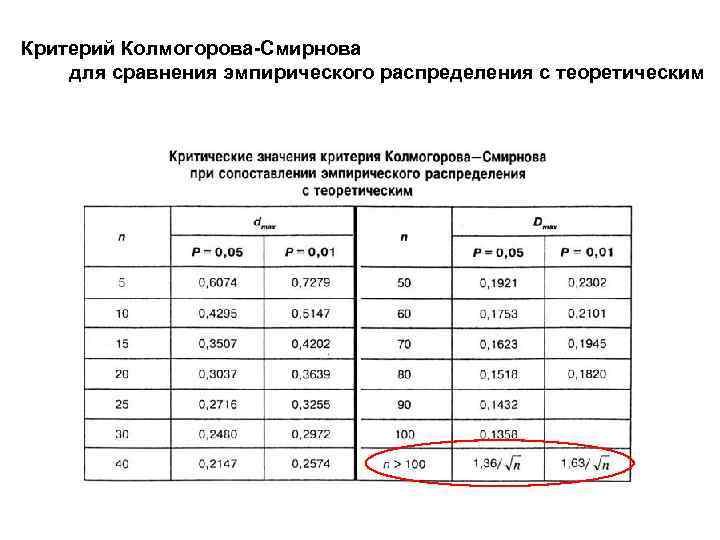 Критерий Колмогорова-Смирнова для сравнения эмпирического распределения с теоретическим
Критерий Колмогорова-Смирнова для сравнения эмпирического распределения с теоретическим
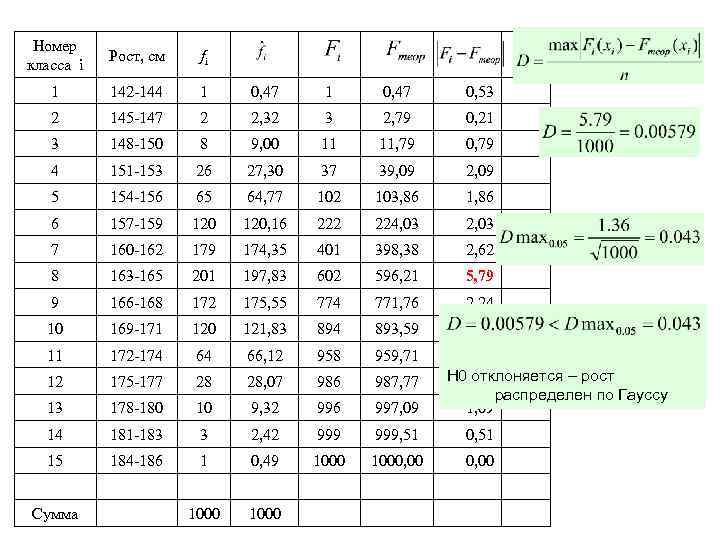 Номер класса i Рост, см fi 1 142 -144 1 0, 47 0, 53 2 145 -147 2 2, 32 3 2, 79 0, 21 3 148 -150 8 9, 00 11 11, 79 0, 79 4 151 -153 26 27, 30 37 39, 09 2, 09 5 154 -156 65 64, 77 102 103, 86 1, 86 6 157 -159 120, 16 222 224, 03 2, 03 7 160 -162 179 174, 35 401 398, 38 2, 62 8 163 -165 201 197, 83 602 596, 21 5, 79 9 166 -168 172 175, 55 774 771, 76 2, 24 10 169 -171 120 121, 83 894 893, 59 0, 41 11 172 -174 64 66, 12 958 959, 71 12 175 -177 28 28, 07 986 987, 77 13 178 -180 10 9, 32 996 997, 09 14 181 -183 3 2, 42 999, 51 0, 51 15 184 -186 1 0, 49 1000, 00 1000 Сумма 1, 71 H 01, 77 отклоняется – рост распределен по Гауссу 1, 09
Номер класса i Рост, см fi 1 142 -144 1 0, 47 0, 53 2 145 -147 2 2, 32 3 2, 79 0, 21 3 148 -150 8 9, 00 11 11, 79 0, 79 4 151 -153 26 27, 30 37 39, 09 2, 09 5 154 -156 65 64, 77 102 103, 86 1, 86 6 157 -159 120, 16 222 224, 03 2, 03 7 160 -162 179 174, 35 401 398, 38 2, 62 8 163 -165 201 197, 83 602 596, 21 5, 79 9 166 -168 172 175, 55 774 771, 76 2, 24 10 169 -171 120 121, 83 894 893, 59 0, 41 11 172 -174 64 66, 12 958 959, 71 12 175 -177 28 28, 07 986 987, 77 13 178 -180 10 9, 32 996 997, 09 14 181 -183 3 2, 42 999, 51 0, 51 15 184 -186 1 0, 49 1000, 00 1000 Сумма 1, 71 H 01, 77 отклоняется – рост распределен по Гауссу 1, 09
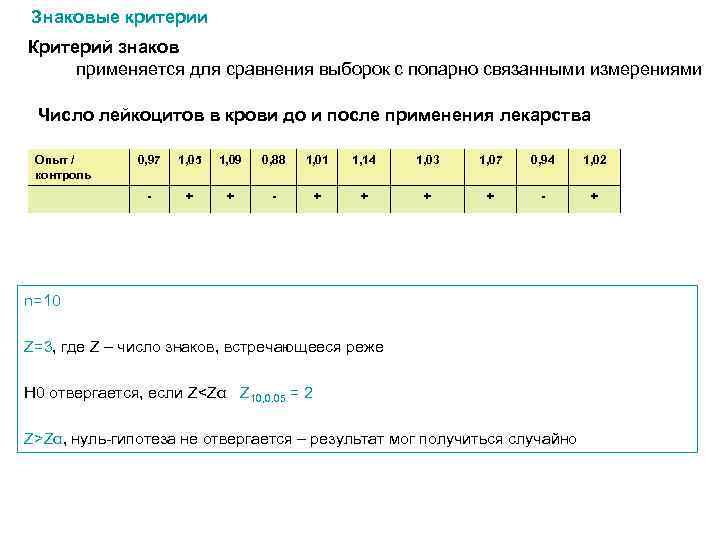 Знаковые критерии Критерий знаков применяется для сравнения выборок с попарно связанными измерениями Число лейкоцитов в крови до и после применения лекарства Опыт / контроль 0, 97 1, 05 1, 09 0, 88 1, 01 1, 14 1, 03 1, 07 0, 94 1, 02 - + + + + - + n=10 Z=3, где Z – число знаков, встречающееся реже Н 0 отвергается, если Z
Знаковые критерии Критерий знаков применяется для сравнения выборок с попарно связанными измерениями Число лейкоцитов в крови до и после применения лекарства Опыт / контроль 0, 97 1, 05 1, 09 0, 88 1, 01 1, 14 1, 03 1, 07 0, 94 1, 02 - + + + + - + n=10 Z=3, где Z – число знаков, встречающееся реже Н 0 отвергается, если Z
 СРАВНЕНИЕ ВЫБОРОК (НЕПАРАМЕТРИЧЕСКОЕ ОЦЕНИВАНИЕ) Критерии: U-Вилкоксона Манна-Уитни Вандер Вардена T Уайда Колмогорова- Смирнова λ Лямбда Q Розенбаума Серийный Знаков Медианы. . . .
СРАВНЕНИЕ ВЫБОРОК (НЕПАРАМЕТРИЧЕСКОЕ ОЦЕНИВАНИЕ) Критерии: U-Вилкоксона Манна-Уитни Вандер Вардена T Уайда Колмогорова- Смирнова λ Лямбда Q Розенбаума Серийный Знаков Медианы. . . .
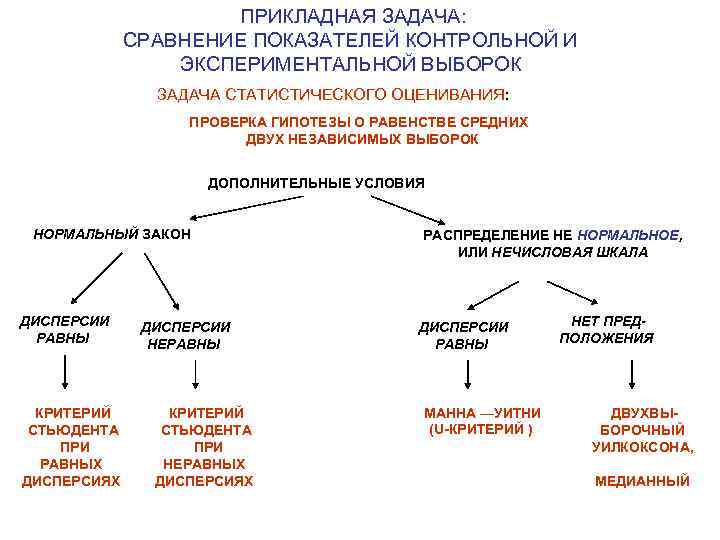 ПРИКЛАДНАЯ ЗАДАЧА: СРАВНЕНИЕ ПОКАЗАТЕЛЕЙ КОНТРОЛЬНОЙ И ЭКСПЕРИМЕНТАЛЬНОЙ ВЫБОРОК ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНИХ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ НОРМАЛЬНЫЙ ЗАКОН ДИСПЕРСИИ РАВНЫ КРИТЕРИЙ СТЬЮДЕНТА ПРИ РАВНЫХ ДИСПЕРСИЯХ ДИСПЕРСИИ НЕРАВНЫ КРИТЕРИЙ СТЬЮДЕНТА ПРИ НЕРАВНЫХ ДИСПЕРСИЯХ РАСПРЕДЕЛЕНИЕ НЕ НОРМАЛЬНОЕ, ИЛИ НЕЧИСЛОВАЯ ШКАЛА ДИСПЕРСИИ РАВНЫ МАННА —УИТНИ (U-КРИТЕРИЙ ) НЕТ ПРЕДПОЛОЖЕНИЯ ДВУХВЫБОРОЧНЫЙ УИЛКОКСОНА, МЕДИАННЫЙ
ПРИКЛАДНАЯ ЗАДАЧА: СРАВНЕНИЕ ПОКАЗАТЕЛЕЙ КОНТРОЛЬНОЙ И ЭКСПЕРИМЕНТАЛЬНОЙ ВЫБОРОК ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНИХ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ НОРМАЛЬНЫЙ ЗАКОН ДИСПЕРСИИ РАВНЫ КРИТЕРИЙ СТЬЮДЕНТА ПРИ РАВНЫХ ДИСПЕРСИЯХ ДИСПЕРСИИ НЕРАВНЫ КРИТЕРИЙ СТЬЮДЕНТА ПРИ НЕРАВНЫХ ДИСПЕРСИЯХ РАСПРЕДЕЛЕНИЕ НЕ НОРМАЛЬНОЕ, ИЛИ НЕЧИСЛОВАЯ ШКАЛА ДИСПЕРСИИ РАВНЫ МАННА —УИТНИ (U-КРИТЕРИЙ ) НЕТ ПРЕДПОЛОЖЕНИЯ ДВУХВЫБОРОЧНЫЙ УИЛКОКСОНА, МЕДИАННЫЙ
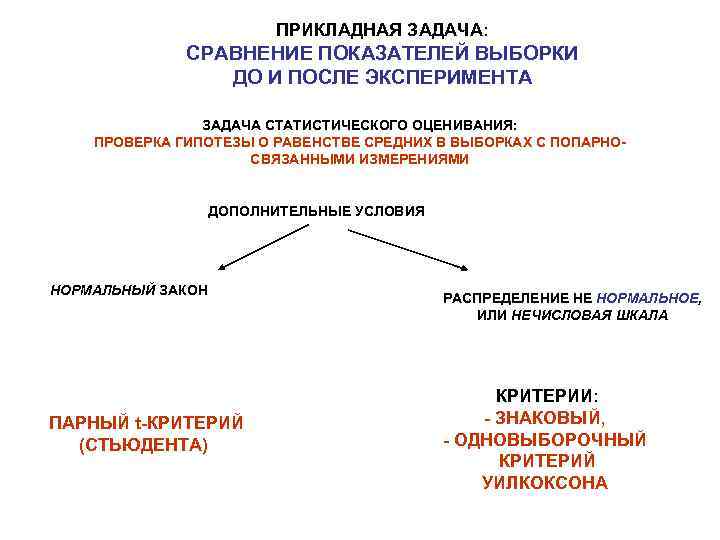 ПРИКЛАДНАЯ ЗАДАЧА: СРАВНЕНИЕ ПОКАЗАТЕЛЕЙ ВЫБОРКИ ДО И ПОСЛЕ ЭКСПЕРИМЕНТА ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНИХ В ВЫБОРКАХ С ПОПАРНОСВЯЗАННЫМИ ИЗМЕРЕНИЯМИ ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ НОРМАЛЬНЫЙ ЗАКОН ПАРНЫЙ t-КРИТЕРИЙ (СТЬЮДЕНТА) РАСПРЕДЕЛЕНИЕ НЕ НОРМАЛЬНОЕ, ИЛИ НЕЧИСЛОВАЯ ШКАЛА КРИТЕРИИ: - ЗНАКОВЫЙ, - ОДНОВЫБОРОЧНЫЙ КРИТЕРИЙ УИЛКОКСОНА
ПРИКЛАДНАЯ ЗАДАЧА: СРАВНЕНИЕ ПОКАЗАТЕЛЕЙ ВЫБОРКИ ДО И ПОСЛЕ ЭКСПЕРИМЕНТА ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНИХ В ВЫБОРКАХ С ПОПАРНОСВЯЗАННЫМИ ИЗМЕРЕНИЯМИ ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ НОРМАЛЬНЫЙ ЗАКОН ПАРНЫЙ t-КРИТЕРИЙ (СТЬЮДЕНТА) РАСПРЕДЕЛЕНИЕ НЕ НОРМАЛЬНОЕ, ИЛИ НЕЧИСЛОВАЯ ШКАЛА КРИТЕРИИ: - ЗНАКОВЫЙ, - ОДНОВЫБОРОЧНЫЙ КРИТЕРИЙ УИЛКОКСОНА
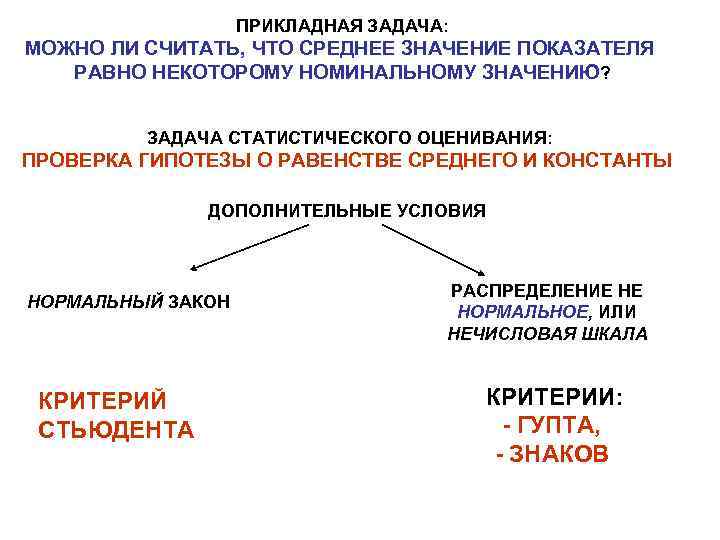 ПРИКЛАДНАЯ ЗАДАЧА: МОЖНО ЛИ СЧИТАТЬ, ЧТО СРЕДНЕЕ ЗНАЧЕНИЕ ПОКАЗАТЕЛЯ РАВНО НЕКОТОРОМУ НОМИНАЛЬНОМУ ЗНАЧЕНИЮ? ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНЕГО И КОНСТАНТЫ ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ НОРМАЛЬНЫЙ ЗАКОН КРИТЕРИЙ СТЬЮДЕНТА РАСПРЕДЕЛЕНИЕ НЕ НОРМАЛЬНОЕ, ИЛИ НЕЧИСЛОВАЯ ШКАЛА КРИТЕРИИ: - ГУПТА, - ЗНАКОВ
ПРИКЛАДНАЯ ЗАДАЧА: МОЖНО ЛИ СЧИТАТЬ, ЧТО СРЕДНЕЕ ЗНАЧЕНИЕ ПОКАЗАТЕЛЯ РАВНО НЕКОТОРОМУ НОМИНАЛЬНОМУ ЗНАЧЕНИЮ? ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНЕГО И КОНСТАНТЫ ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ НОРМАЛЬНЫЙ ЗАКОН КРИТЕРИЙ СТЬЮДЕНТА РАСПРЕДЕЛЕНИЕ НЕ НОРМАЛЬНОЕ, ИЛИ НЕЧИСЛОВАЯ ШКАЛА КРИТЕРИИ: - ГУПТА, - ЗНАКОВ
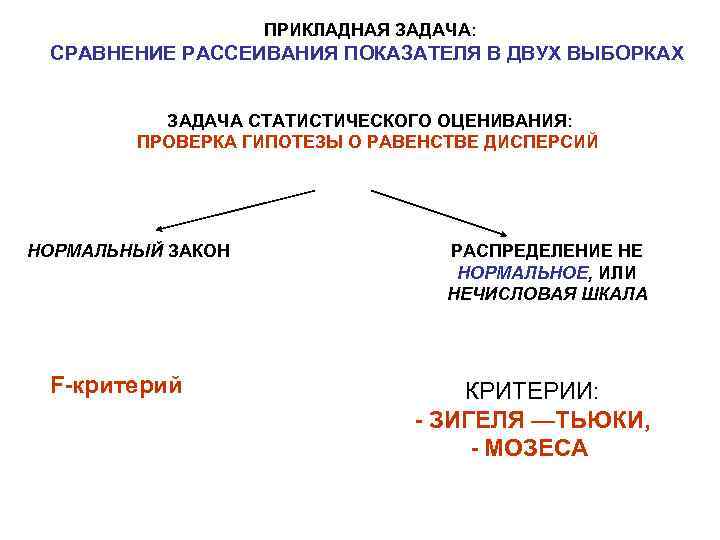 ПРИКЛАДНАЯ ЗАДАЧА: СРАВНЕНИЕ РАССЕИВАНИЯ ПОКАЗАТЕЛЯ В ДВУХ ВЫБОРКАХ ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ДИСПЕРСИЙ НОРМАЛЬНЫЙ ЗАКОН F-критерий РАСПРЕДЕЛЕНИЕ НЕ НОРМАЛЬНОЕ, ИЛИ НЕЧИСЛОВАЯ ШКАЛА КРИТЕРИИ: - ЗИГЕЛЯ —ТЬЮКИ, - МОЗЕСА
ПРИКЛАДНАЯ ЗАДАЧА: СРАВНЕНИЕ РАССЕИВАНИЯ ПОКАЗАТЕЛЯ В ДВУХ ВЫБОРКАХ ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ДИСПЕРСИЙ НОРМАЛЬНЫЙ ЗАКОН F-критерий РАСПРЕДЕЛЕНИЕ НЕ НОРМАЛЬНОЕ, ИЛИ НЕЧИСЛОВАЯ ШКАЛА КРИТЕРИИ: - ЗИГЕЛЯ —ТЬЮКИ, - МОЗЕСА
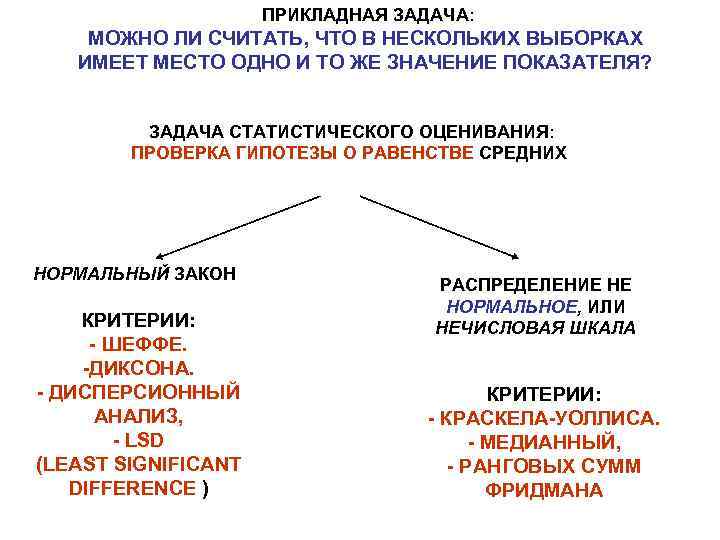 ПРИКЛАДНАЯ ЗАДАЧА: МОЖНО ЛИ СЧИТАТЬ, ЧТО В НЕСКОЛЬКИХ ВЫБОРКАХ ИМЕЕТ МЕСТО ОДНО И ТО ЖЕ ЗНАЧЕНИЕ ПОКАЗАТЕЛЯ? ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНИХ НОРМАЛЬНЫЙ ЗАКОН КРИТЕРИИ: - ШЕФФЕ. -ДИКСОНА. - ДИСПЕРСИОННЫЙ АНАЛИЗ, - LSD (LEAST SIGNIFICANT DIFFERENCE ) РАСПРЕДЕЛЕНИЕ НЕ НОРМАЛЬНОЕ, ИЛИ НЕЧИСЛОВАЯ ШКАЛА КРИТЕРИИ: - КРАСКЕЛА-УОЛЛИСА. - МЕДИАННЫЙ, - РАНГОВЫХ СУММ ФРИДМАНА
ПРИКЛАДНАЯ ЗАДАЧА: МОЖНО ЛИ СЧИТАТЬ, ЧТО В НЕСКОЛЬКИХ ВЫБОРКАХ ИМЕЕТ МЕСТО ОДНО И ТО ЖЕ ЗНАЧЕНИЕ ПОКАЗАТЕЛЯ? ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНИХ НОРМАЛЬНЫЙ ЗАКОН КРИТЕРИИ: - ШЕФФЕ. -ДИКСОНА. - ДИСПЕРСИОННЫЙ АНАЛИЗ, - LSD (LEAST SIGNIFICANT DIFFERENCE ) РАСПРЕДЕЛЕНИЕ НЕ НОРМАЛЬНОЕ, ИЛИ НЕЧИСЛОВАЯ ШКАЛА КРИТЕРИИ: - КРАСКЕЛА-УОЛЛИСА. - МЕДИАННЫЙ, - РАНГОВЫХ СУММ ФРИДМАНА
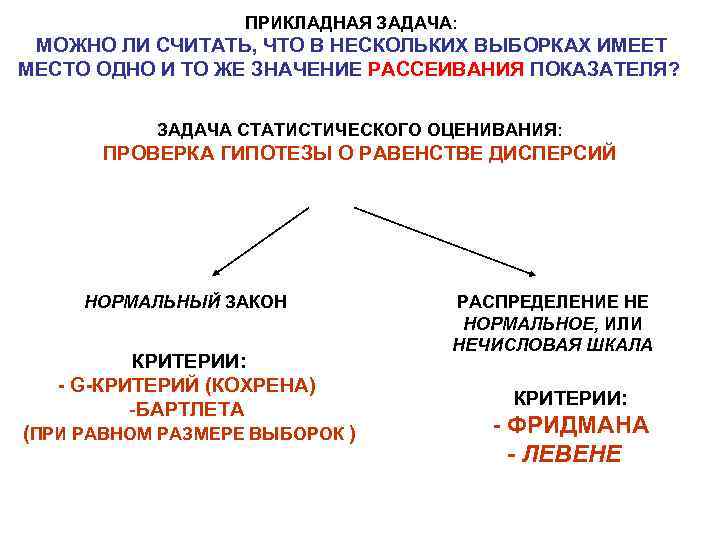 ПРИКЛАДНАЯ ЗАДАЧА: МОЖНО ЛИ СЧИТАТЬ, ЧТО В НЕСКОЛЬКИХ ВЫБОРКАХ ИМЕЕТ МЕСТО ОДНО И ТО ЖЕ ЗНАЧЕНИЕ РАССЕИВАНИЯ ПОКАЗАТЕЛЯ? ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ДИСПЕРСИЙ НОРМАЛЬНЫЙ ЗАКОН КРИТЕРИИ: - G-КРИТЕРИЙ (КОХРЕНА) -БАРТЛЕТА (ПРИ РАВНОМ РАЗМЕРЕ ВЫБОРОК ) РАСПРЕДЕЛЕНИЕ НЕ НОРМАЛЬНОЕ, ИЛИ НЕЧИСЛОВАЯ ШКАЛА КРИТЕРИИ: - ФРИДМАНА - ЛЕВЕНЕ
ПРИКЛАДНАЯ ЗАДАЧА: МОЖНО ЛИ СЧИТАТЬ, ЧТО В НЕСКОЛЬКИХ ВЫБОРКАХ ИМЕЕТ МЕСТО ОДНО И ТО ЖЕ ЗНАЧЕНИЕ РАССЕИВАНИЯ ПОКАЗАТЕЛЯ? ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ДИСПЕРСИЙ НОРМАЛЬНЫЙ ЗАКОН КРИТЕРИИ: - G-КРИТЕРИЙ (КОХРЕНА) -БАРТЛЕТА (ПРИ РАВНОМ РАЗМЕРЕ ВЫБОРОК ) РАСПРЕДЕЛЕНИЕ НЕ НОРМАЛЬНОЕ, ИЛИ НЕЧИСЛОВАЯ ШКАЛА КРИТЕРИИ: - ФРИДМАНА - ЛЕВЕНЕ
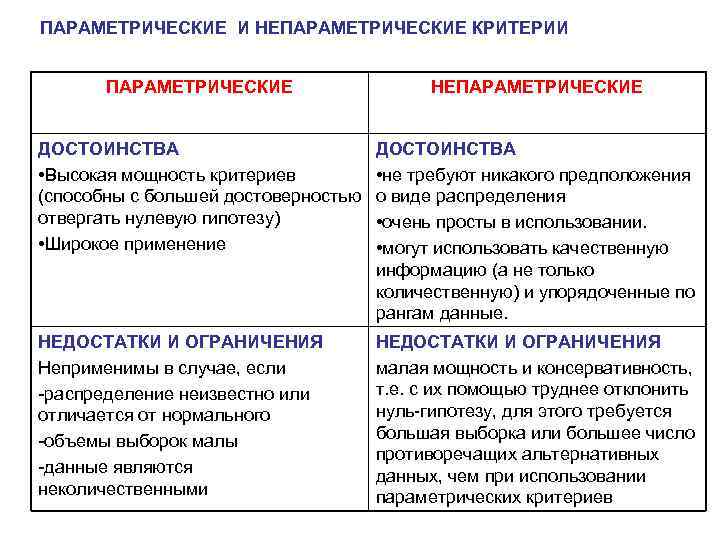 ПАРАМЕТРИЧЕСКИЕ И НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ ПАРАМЕТРИЧЕСКИЕ НЕПАРАМЕТРИЧЕСКИЕ ДОСТОИНСТВА • Высокая мощность критериев (способны с большей достоверностью отвергать нулевую гипотезу) • Широкое применение ДОСТОИНСТВА • не требуют никакого предположения о виде распределения • очень просты в использовании. • могут использовать качественную информацию (а не только количественную) и упорядоченные по рангам данные. НЕДОСТАТКИ И ОГРАНИЧЕНИЯ Неприменимы в случае, если -распределение неизвестно или отличается от нормального -объемы выборок малы -данные являются неколичественными НЕДОСТАТКИ И ОГРАНИЧЕНИЯ малая мощность и консервативность, т. е. с их помощью труднее отклонить нуль-гипотезу, для этого требуется большая выборка или большее число противоречащих альтернативных данных, чем при использовании параметрических критериев
ПАРАМЕТРИЧЕСКИЕ И НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ ПАРАМЕТРИЧЕСКИЕ НЕПАРАМЕТРИЧЕСКИЕ ДОСТОИНСТВА • Высокая мощность критериев (способны с большей достоверностью отвергать нулевую гипотезу) • Широкое применение ДОСТОИНСТВА • не требуют никакого предположения о виде распределения • очень просты в использовании. • могут использовать качественную информацию (а не только количественную) и упорядоченные по рангам данные. НЕДОСТАТКИ И ОГРАНИЧЕНИЯ Неприменимы в случае, если -распределение неизвестно или отличается от нормального -объемы выборок малы -данные являются неколичественными НЕДОСТАТКИ И ОГРАНИЧЕНИЯ малая мощность и консервативность, т. е. с их помощью труднее отклонить нуль-гипотезу, для этого требуется большая выборка или большее число противоречащих альтернативных данных, чем при использовании параметрических критериев


