Непараметрические критерии 1 Непараметрический критерий Вилкоксона 2

Непараметрические критерии

1. Непараметрический критерий Вилкоксона 2. Критерий Уайта 3. Критерий Знаков

В последнее время в математической статистике интенсивно разрабатываются непараметрические методы, которые строятся на как можно меньшем количестве допущений Ранг – порядковый номер выборочного значения, если в выборке нет совпадающих значений Если же они есть, то ранг определяется как среднее арифметическое порядковых номеров совпадающих значений

Критерий Вилкоксона Это непараметрический критерий - аналог параметрического критерия Стьюдента для связанных выборок, т. е. выборок, полученных при парных сравнениях Количество элементов в выборках должно быть одинаковым

§ § § § Алгоритм применения: Задаем уровень значимости Записываем значения выборок xi и yi в виде столбцов попарно Отбрасываем пары с одинаковыми значениями xi и yi и для дальнейших расчетов объем выборки (количество пар значений) сокращаем на число отброшенных пар Находим разности каждой пары значений (xi - yi) и обозначаем эту разность di Находим ранги абсолютных значений разностей пар значений di (начинаем проставлять ранги с самой маленькой разности) Отдельно записываем ранги, относящиеся к положительным и отрицательным значениям разностей Находим по отдельности суммы рангов отрицательных и положительных разностей

§ Меньшую из найденных сумм принимаем в качестве расчетного критерия Вилкоксона (Wp). § Из таблицы критических значений критерия Вилкоксона находим граничное значения критерия Wгр при заданном уровне значимости и объеме выборки N. § Делаем вывод: если расчетное значение критерия Вилкоксона меньше или равно граничному значению ( Wр < Wгр), то нулевая гипотеза отбрасывается и наблюдаемое различие связанных выборок является статистически значимым. В противном случае различие статистически недостоверно.

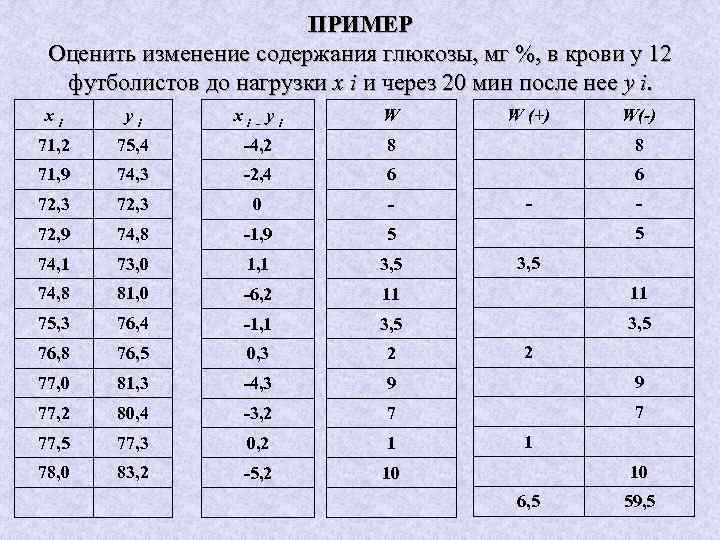ПРИМЕР Оценить изменение содержания глюкозы, мг %, в крови у 12 футболистов до нагрузки х і и через 20 мин после нее у і. хі уі хі - уі W W (+) 71, 2 75, 4 -4, 2 8 8 71, 9 74, 3 -2, 4 6 6 72, 3 0 - 72, 9 74, 8 -1, 9 5 74, 1 73, 0 1, 1 3, 5 74, 8 81, 0 -6, 2 11 11 75, 3 76, 4 -1, 1 3, 5 76, 8 76, 5 0, 3 2 77, 0 81, 3 -4, 3 9 9 77, 2 80, 4 -3, 2 7 7 77, 5 77, 3 0, 2 1 78, 0 83, 2 -5, 2 10 - W(-) 5 3, 5 2 1 10 6, 5 59, 5

Решение: § Сравним исходные данные при помощи критерия Вилкоксона (попарно). § Критерий определим как меньшую из сумм рангов, назначенных положительным и отрицательным попарным разностям исходных данных W = 6, 5. § Определим граничное значение критерия из таблицы Вилкоксона при надежности Р = 0, 95 (или уровне значимости р=0, 05) и объеме n = 11, т. е. по числу рассмотренных пар без одного нулевого значения n = 12 Wгр = 15.

Вывод: § Поскольку Wр < Wгр. , приходим к выводу о статистически достоверном различии между исходными данными. Таким образом, у испытуемых существенно увеличилось содержание глюкозы в крови после тренировочной нагрузки. Это, по-видимому, свидетельствует об эффективности предложенной нагрузки.

Критерий Уайта Критерий применяется при сравнении двух больших, независимых разновеликих выборок для установления достоверности различий

Алгоритм применения: § Задается уровень значимости § Эмпирические данные ранжируются по двум линиям, которые соответствуют исследуемым группам. Ранжирование производится одновременно для обеих групп § Полученные ранги суммируются по каждой линии отдельно и меньшая из сумм принимается за расчетное значение критерия § По таблице для заданной надежности и соответствующих объемов выборок находим граничное значение критерия Уайта § Если расчетное значение критерия Тр меньше или равно граничному значению Тгр, то различие между выборками есть статистически значимым. В противном случае различие статистически недостоверно и выборочные значения можно считать одинаковыми.

Пример. Два пловца X и Y в равноценных условиях 10 раз проплыли 25 метровую дистанцию. Проанализировав время прохождения дистанции первым xi (мс– 1) и вторым уi (мс– 1) пловцами, определить достоверность различия полученных данных. Время прохождения дистанции первым xi (мс– 1) и вторым уi (мс– 1) пловцами xi 12, 4 12, 5 12, 3 12, 8 12, 5 12, 0 12, 2 12, 4 12, 3 12, 7 уi 12, 8 12, 9 12, 5 12, 4 12, 7 12, 5 12, 8 12, 3 12, 5 12, 2

Решение: § Ранжируем данные и присваиваем им ранги Rxi 1 2, 5 5 5 8 8 12 12 15, 5 18 xi 12, 0 12, 2 12, 3 12, 4 12, 5 12, 7 12, 8 Ryi 2, 5 5 8 12 12 12 15, 5 18 18 20 yi 12, 2 12, 3 12, 4 12, 5 12, 7 12, 8 12, 9 § Суммируем ранги отдельно R хi и R уi Тх = 1+ 2, 5 + 5 + 8+ 12 + 15, 5 + 18 = 87, 0 Ту = 2, 5 + 8 + 12 + 15, 5 + 18 + 20 = 123, 0 § Меньшая из сумм принимается за расчетное значение критерия Уайта — Тр = 87, 0 § По таблице граничных значений критерия Уайта при заданном уровне значимости р = 0, 05 и количестве эмпиричных измерений пх — пу = 10 находим граничное значение критерия Тгр = 78

Вывод: Поскольку Трасч > Тгр, то различие между выборками статистически недостоверно. Показатели обоих пловцов на 25 -метровой дистанции существенно не отличаются, пловцы — спортсмены одной квалификации

Критерий знаков Этот критерий применяется при сравнении больших, равновесных выборок с попарно сопряженными вариантами. Такие задачи встречаются в тех случаях, когда рассматривается один и тот же объект до и после опыта или сравнивается аналогичный признак в нескольких группах, например, в контрольной и экспериментальной

Алгоритм применения: § Задается уровень значимости § Записываем значения выборок xi и yi в виде столбцов попарно § В третьем столбце улучшение результата обозначается знаком плюс (+), ухудшение — знаком минус (–). Необходимо помнить о том, что в практике спорта под улучшением в одних случаях понимается увеличение абсолютного значения (прирост силы, веса, расстояния), в других случаях — уменьшение (время прохождения дистанции) § Подсчитываются суммы положительных, отрицательных и нулевых изменений § Сумма отрицательных изменений – расчетное значения критерия «знаков» Zp § По таблице границ критической области критерия «знаков» (при заданной надежности и количестве исследуемых пар n без нулевых значений) находят граничное значение критерия "знаков" Zrp — это интервал

§ Сумма отрицательных изменений – расчетное значения критерия «знаков» Zp § По таблице границ критической области критерия «знаков» (при заданной надежности и количестве исследуемых пар n без нулевых значений) находят граничное значение критерия "знаков" Zrp — это интервал § При попадании количества отрицательных изменений внутрь этого интервала наблюдается статистическая недостоверность между исследуемыми показателями в сравниваемых группах, в противоположном случае — статистическая достоверность различия.

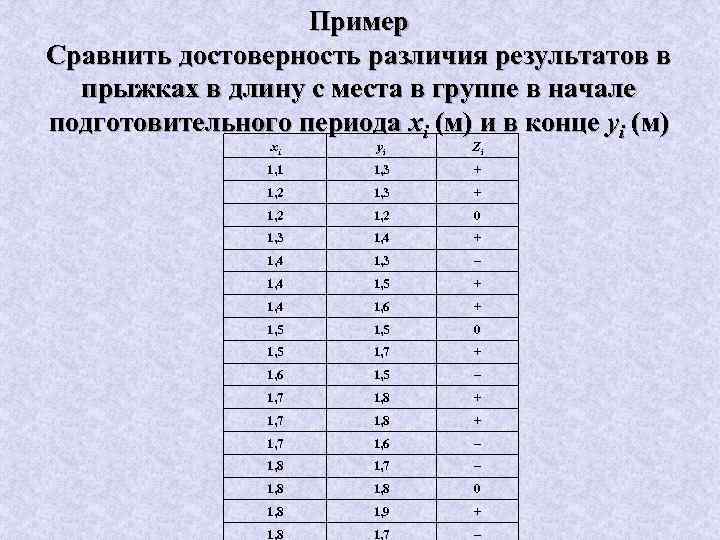Пример Сравнить достоверность различия результатов в прыжках в длину с места в группе в начале подготовительного периода хi (м) и в конце уi (м) xi yi Zi 1, 1 1, 3 + 1, 2 0 1, 3 1, 4 + 1, 4 1, 3 – 1, 4 1, 5 + 1, 4 1, 6 + 1, 5 0 1, 5 1, 7 + 1, 6 1, 5 – 1, 7 1, 8 + 1, 7 1, 6 – 1, 8 1, 7 – 1, 8 0 1, 8 1, 9 + 1, 8 1, 7 –

Решение: § Подсчитываем количество положительных, отрицательных и нулевых значений: Z(+) = 9, Z(–) = 5, Z(0) = 3 § Задаем уровень значимости р = 0, 05 и находим расчетный объем n = n — Z(0) = 17 — 3 = 14 § По таблице критерия «знаков» находим искомый интервал Zгp = 3. . . 11

Вывод: Так как Z(–) = 5 находится внутри этого интервала, то различие между показателями статистически недостоверно. Это значит, что параметр — прыжок в длину с места (м) не изменился в течение подготовительного периода во всей группе. Тренировочные занятия на развитие данного параметра должны быть интенсифицированы