Неопределенный интеграл Функция F(x) наз. первообразной для функции f(x), если F′(x) = f(x). Неопределенный интеграл от f(x) - совокупность всех ее первообразных: ∫ знак интеграла, f(x)dx подынтегральное выражение, x – переменная интегрирования.
Свойства интеграла Производная неопределенного интеграла равна подынтегральной функции, а его дифференциалподынтегральному выражению. 1. . 2. 3. где а = const
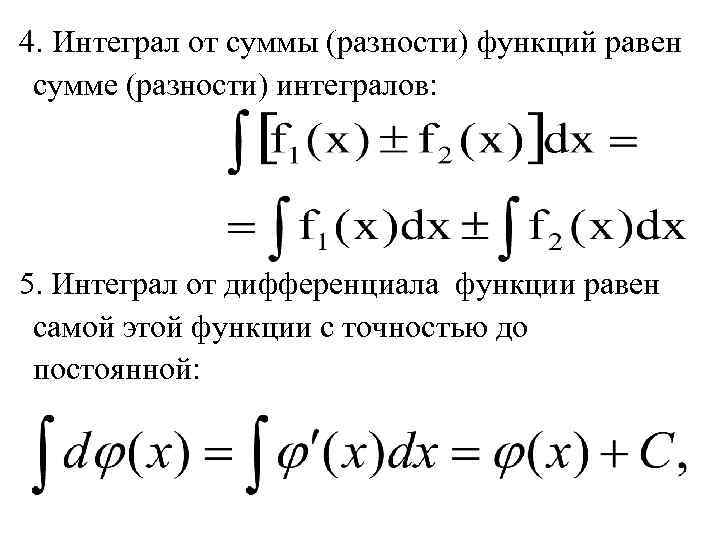
4. Интеграл от суммы (разности) функций равен сумме (разности) интегралов: 5. Интеграл от дифференциала функции равен самой этой функции с точностью до постоянной:
Таблица неопределенных интегралов
Таблица неопределенных интегралов
Основные методы интегрирования: - Замена переменной. - Интегрирование по частям. - Метод неопределённых коэффициентов.
Метод замены переменной. Если требуется найти интеграл , но сложно отыскать первообразную, то с помощью замены x = (t) и dx = (t)dt получается:
При замене переменной выполняют следующие преобразования:
Пример: Вычислить.
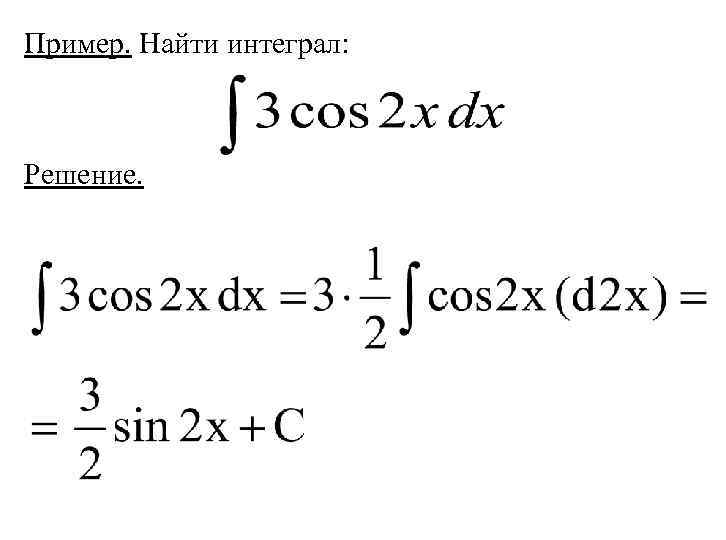
Пример. Найти интеграл: Решение.
•
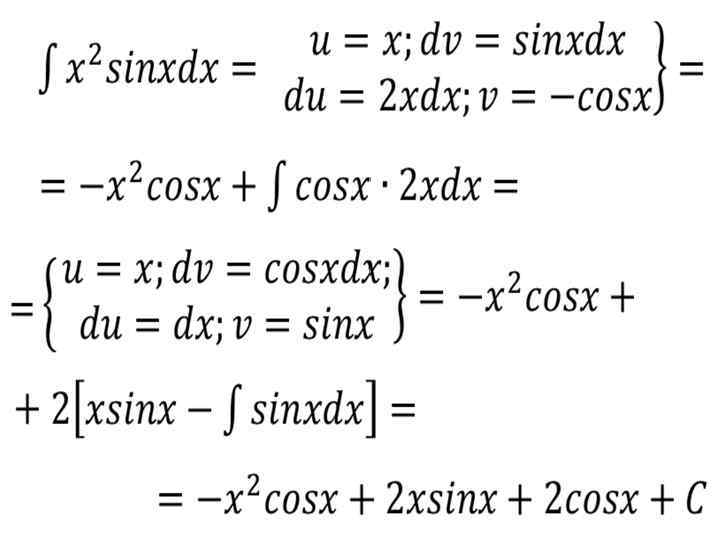
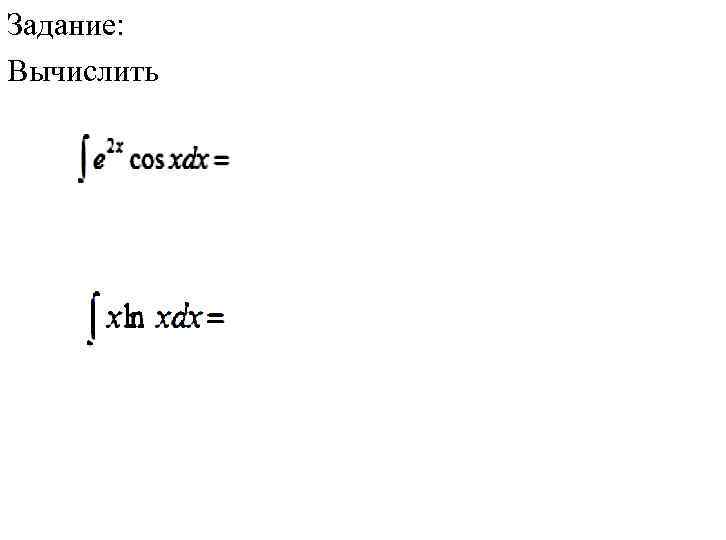
Задание: Вычислить
![Определённый интеграл Пусть функция f(x)определена на отрезке [a, b], который разделим на п произвольных](https://present5.com/presentation/1/53467862_158643632.pdf-img/53467862_158643632.pdf-15.jpg "Определённый интеграл Пусть функция f(x)определена на отрезке [a, b], который разделим на п произвольных")
Определённый интеграл Пусть функция f(x)определена на отрезке [a, b], который разделим на п произвольных частей точками: выберем на каждом отрезке точку произвольную и найдем длину отрезка: Интегральной суммой для функции f(x) на отрезке [a, b] называют сумму: причем эта сумма имеет конечный предел I, если для каждого найдется такое число неравенство , что при верно при любом выборе .
Основные свойства определенного интеграла
Приложение определенного интеграла - вычисление площади криволинейной трапеции Криволинейной трапецией наз. фигура, ограниченная графиком непрерывной, неотрицательной функции f(x) на промежутке [a; b], отрезками прямых x = a и x = b, а также отрезком оси абсцисс между точками a и b.
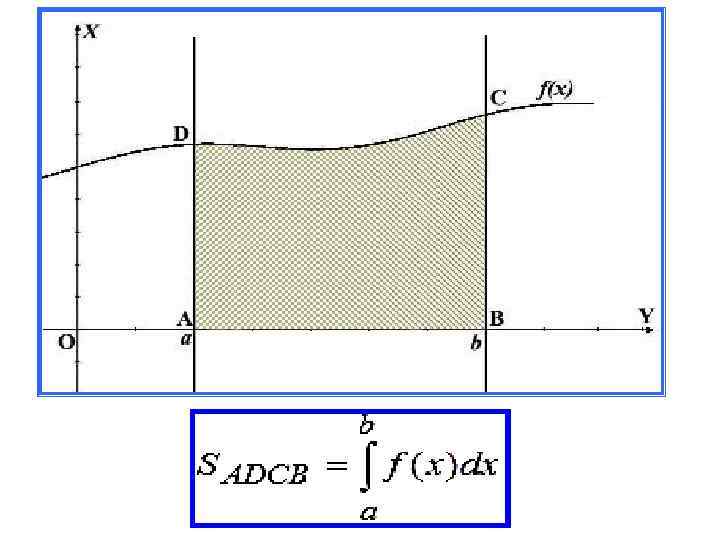
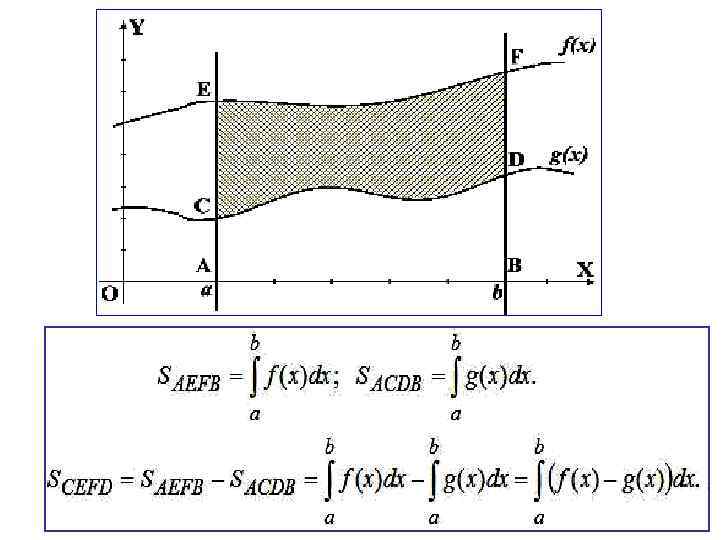
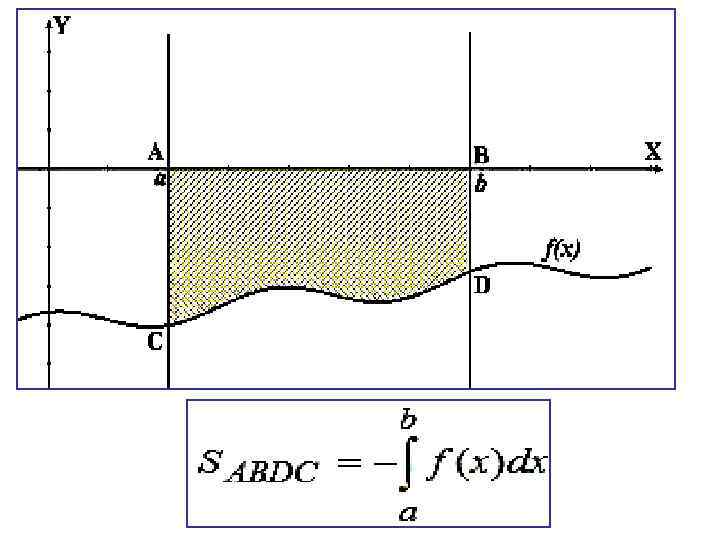
Пример. Вычислить площадь фигуры, ограниченной линиями у = , х = 3, y = 0. Решение: Криволинейная трапеция имеет вид:
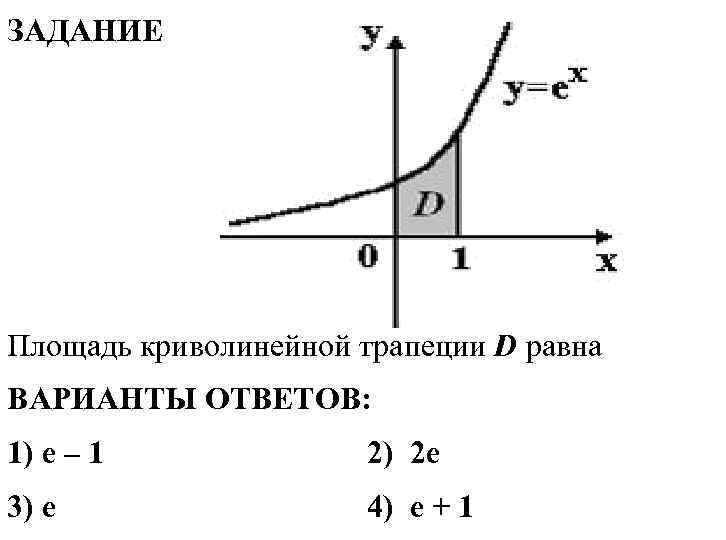
ЗАДАНИЕ Площадь криволинейной трапеции D равна ВАРИАНТЫ ОТВЕТОВ: 1) e – 1 2) 2 e 3) e 4) e + 1
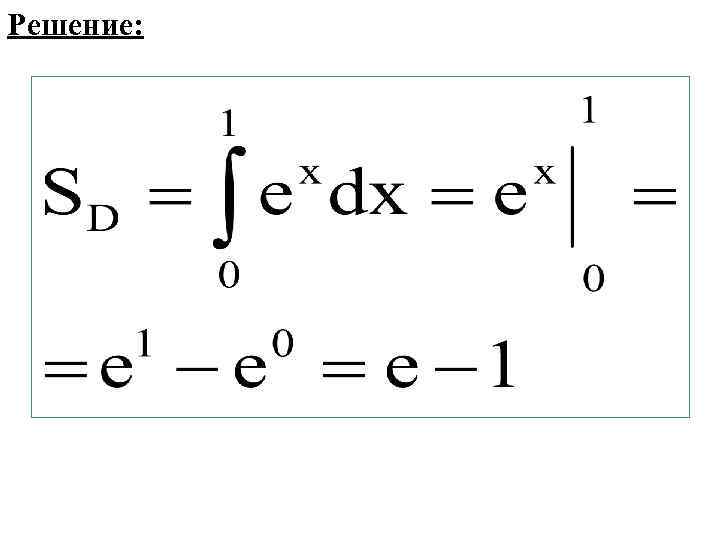
Решение:
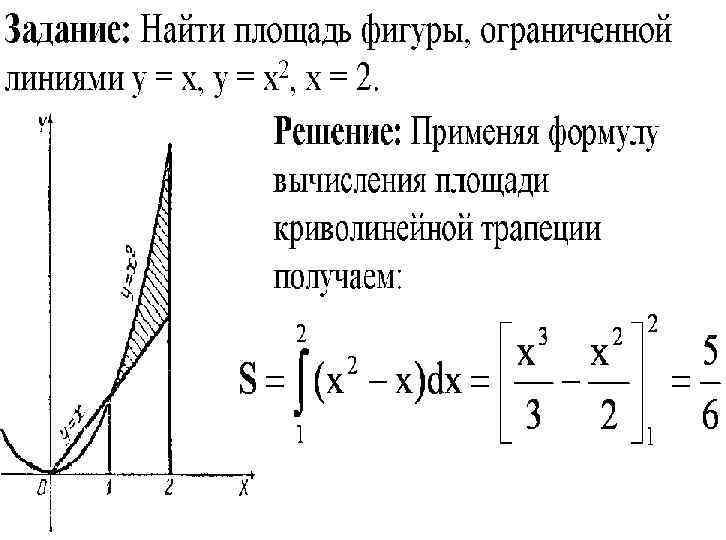
Домашняя задача Вычислить площадь фигуры, ограниченной линиями у = x 2 + 2 x и y = x + 2.
•
•
Пример: - не существует. Несобственный интеграл расходится. - интеграл сходится
. яаамгетнтееассядндюлилс. В ллсрритясдяавчози с охоооб. Е гещя иосяы сат с охсар ни иетиттон м стэт а хж ул х д ти , . Если для всех х (x ≥ a) выполняется условие и интеграл тоже сходится и сходится, то ≥ . Если для всех х (x ≤ a) выполняется условие и интеграл расходится, то
Домашняя работа 1. Найти производную функции: Y= 3·cos 4 x 2 2. Вычислить интеграл:
Скачать презентацию Неопределенный интеграл Функция F x наз первообразной для функции
интеграл.pptx