НЕЛОКАЛЬНЫЕ ЗАКОНОМЕРНОСТИ ДИАГРАММ ФАЗОВОГО РАВНОВЕСИЯ НА ПРИМЕРЕ СИСТЕМ

НЕЛОКАЛЬНЫЕ ЗАКОНОМЕРНОСТИ ДИАГРАММ ФАЗОВОГО РАВНОВЕСИЯ НА ПРИМЕРЕ СИСТЕМ ЖИДКОСТЬ - ПАР ТЕМА 3 1

НЕЛОКАЛЬНЫЕ ЗАКОНОМЕРНОСТИ ФАЗОВЫХ ДИАГРАММ (закономерности, относящиеся к диаграмме в целом) • Баланс топологических индексов. • Перенос концентрационного симплекса (пространство с краем) на сферу (каждая точка получает полную окрестность) – замкнутое многообразие. Индекс особой точки (i) Знак индекса особой точки равен знаку произведения характеристических корней. Определение индекса особой точки (тройная система) Устойчивый узелλ >0 Sign П λ > 0 i = 3600 / 3600 = 1 2

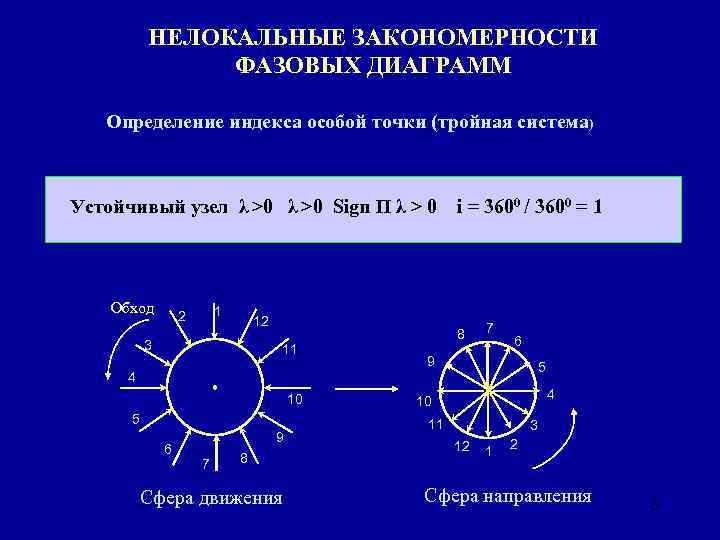НЕЛОКАЛЬНЫЕ ЗАКОНОМЕРНОСТИ ФАЗОВЫХ ДИАГРАММ Определение индекса особой точки (тройная система) Устойчивый узел λ >0 Sign П λ > 0 i = 3600 / 3600 = 1 Обход 1 2 12 3 11 8 7 6 9 5 4 10 5 6 9 7 8 Сфера движения 4 10 11 3 12 1 2 Сфера направления 3

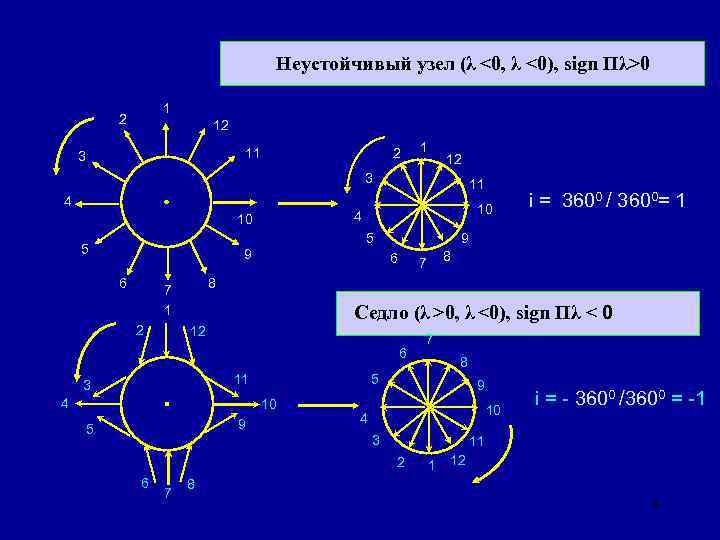Неустойчивый узел (λ <0, λ <0), sign Пλ>0 1 2 12 11 3 2 1 12 3 4 11 10 4 10 5 5 9 6 8 7 1 2 Седло (λ >0, λ <0), sign Пλ < 0 12 6 4 10 9 5 7 8 5 11 3 9 10 4 3 7 i = - 3600 /3600 = -1 11 2 6 i = 3600 / 3600= 1 1 12 8 4

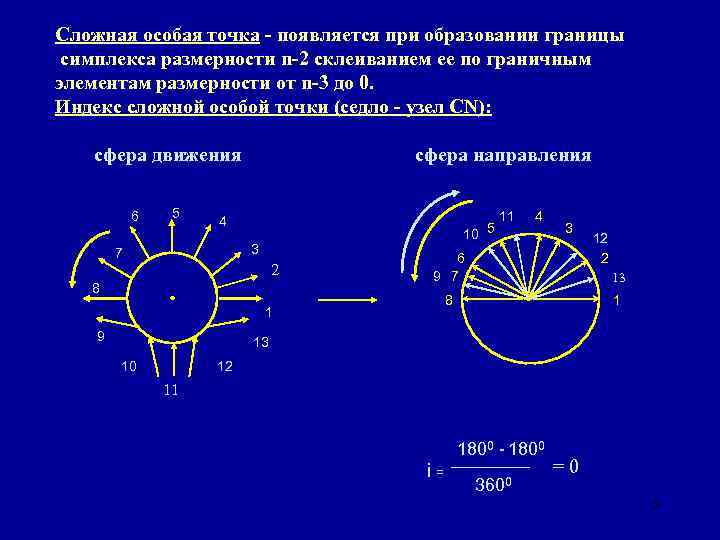Сложная особая точка - появляется при образовании границы симплекса размерности n-2 склеиванием ее по граничным элементам размерности от n-3 до 0. Индекс сложной особой точки (седло - узел CN): сфера движения 6 5 сфера направления 4 10 5 3 7 2 8 4 3 6 9 7 12 2 13 8 1 9 11 1 13 10 12 11 i= 1800 - 1800 3600 =0 5

БАЛАНС ИНДЕКСОВ ОСОБЫХ ТОЧЕК Теорема Кронекера Σ i = I = Э = 1 + (-1)m I – индекс замкнутого многообразия (сферы) Э – характеристика сферы Эйлера m – размерность сферы 6

Отображение концентрационного симплекса тройной системы на сферу Метод Жарова В. Т. (ЛГУ) (конверт Гурикова – склеиваются 8 треугольников) 1 3΄ 2 3 1 2΄ 2΄ 1΄ Каждая точка внутри треугольника повторяется на сфере 8 раз, на стороне – 4 раза, в вершине – 2 раза. 2΄ 3΄ 3 2 1΄ m=2 8 N 3 – 8 C 3 + 4 N 2 – 4 C 2 + 2 N 1 – 2 C 1 = 2 (4. 1) 7

Отображение концентрационного симплекса тройной системы на сферу Метод Серафимова Л. А. (МИТХТ) (склеиваются 2 треугольника) 2 ≡ 2΄ 2΄ 1 ≡ 1΄ 1 3 3 ≡ 3΄ Каждая точка внутри треугольника повторяется на сфере 2 раза; каждая точка на стороне треугольника и вершины треугольника повторяются 1 раз. 2 N 3 – 2 C 3 + N 2 – C 2 + N 1 = 2 (4. 2) C 1 в отображении Серафимова имеет индекс равный нулю как сложная особая точка. Сложные особые точки, образующие на границе концентрационного симплекса, в методе Серафимова не учитываются, т. к. i = 0 8

ТЕМА 4 КЛАССИФИКАЦИЯ ДИАГРАММ ФАЗОВОГО РАВНОВЕСИЯ. ТРОЙНЫЕ МОНОАЗЕОТРОПНЫЕ СИСТЕМЫ ЖИДКОСТЬ – ПАР 9

КЛАСС ДИАГРАММ - определяется количеством особых точек в ней, - записывается в виде последовательного набора чисел, разделенных точкой, где 1 число - число компонентов; 2 число - число бинарных азеотропов (М 2); 3 число - число тройных азеотропов (М 3); и т. д. В общем виде, класс диаграммы трехкомпонентной системы записывается: 3. М 2. М 3 10

Для моноазеотропных систем, когда на каждом элементе диаграммы реализуется только один азеотроп с соответствующим числом компонентов (на стороне треугольника – один бинарный азеотроп; внутри треугольника – один тройной азеотроп), Общее количество особых точек равно: М 2 = N 2 + C 2 М 2 = 0; 1; 2; 3 М 3 = N 3 + C 3 М 2 = 0; 1 3 = N 1 + C 1 где Ni -число узлов Cj - число седел УРАВНЕНИЕ СВЯЗИ ОСОБЫХ ТОЧЕК 2 M 3 + M 2 +N 1 2 где M 2 = 0, 1, 2, 3 - 1 = 2 C 3 + C 2 M 3=0 или 1 11

Класс диаграммы - определяется количеством особых точек в диаграмме. . Тип диаграммы - это диаграммы в пределах одного класса с разным набором типов особых точек (в обозначении диаграммы типу соответствует запись после определения класса цифры « 1» или « 2» и т. д. ). Подтипы диаграмм - это диаграммы в рамках одного типа: - с разным расположением особых точек в симплексе; - с разной укладкой пучка дистилляционных линий. (в обозначении диаграммы подтипам соответствует запись после определения типа буквы «а» , или «б» , или «в» и т. д. ). 12

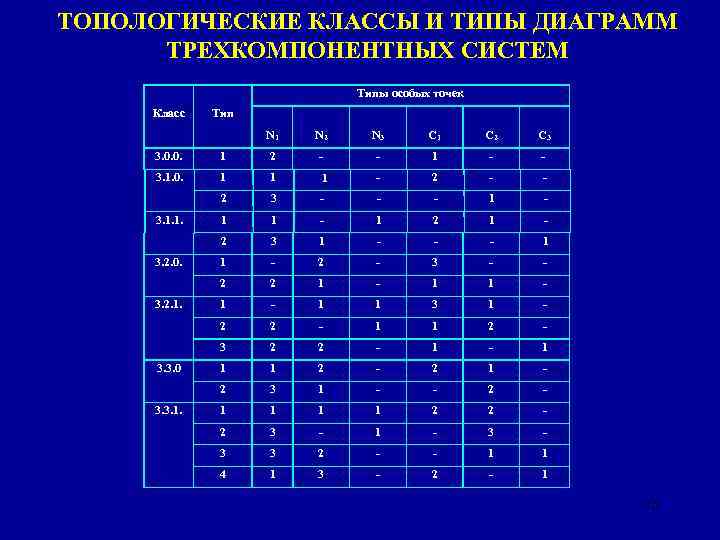ТОПОЛОГИЧЕСКИЕ КЛАССЫ И ТИПЫ ДИАГРАММ ТРЕХКОМПОНЕНТНЫХ СИСТЕМ Типы особых точек Класс Тип N 1 N 2 N 3 C 1 C 2 C 3 3. 0. 0. 1 2 - - 1 - - 3. 1. 0. 1 1 1 - 2 - - 2 3 - - - 1 1 - 1 2 1 - 2 3 1 - - - 1 1 - 2 - 3 - - 2 2 1 - 1 - 1 1 3 1 - 2 2 - 1 1 2 - 3 2 2 - 1 1 1 2 - 2 1 - 2 3 1 - - 2 - 1 1 2 2 - 2 3 - 1 - 3 3 2 - - 1 1 4 1 3 - 2 - 1 3. 1. 1. 3. 2. 0. 3. 2. 1. 3. 3. 0 3. 3. 1. 13

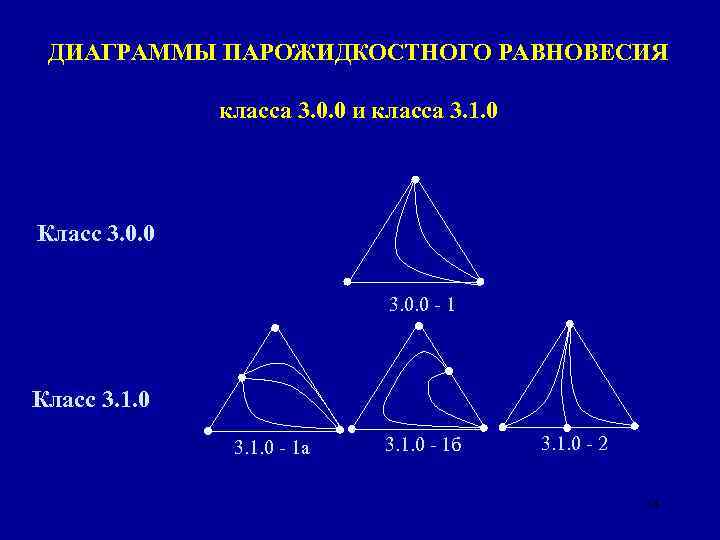ДИАГРАММЫ ПАРОЖИДКОСТНОГО РАВНОВЕСИЯ класса 3. 0. 0 и класса 3. 1. 0 Класс 3. 0. 0 - 1 Класс 3. 1. 0 - 1 а 3. 1. 0 - 1 б 3. 1. 0 - 2 14

ДИАГРАММЫ ПАРОЖИДКОСТНОГО РАВНОВЕСИЯ класса 3. 1. 1 - 1 а 3. 1. 1 - 1 б 3. 1. 1 - 2 15

ДИАГРАММЫ ПАРОЖИДКОСТНОГО РАВНОВЕСИЯ класса 3. 2. 0 - 1 3. 2. 0 - 2 а 3. 2. 0 - 2 б 3. 2. 0 - 2 в 16

ДИАГРАММЫ ПАРОЖИДКОСТНОГО РАВНОВЕСИЯ класса 3. 2. 1 - 1 3. 2. 1 - 2 а 3. 2. 1 - 3 а 3. 2. 1 - 2 б 3. 2. 1 - 3 б 17

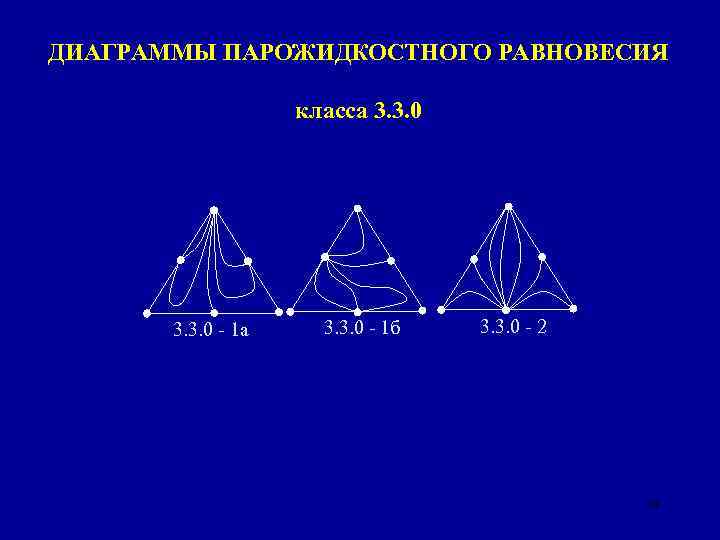ДИАГРАММЫ ПАРОЖИДКОСТНОГО РАВНОВЕСИЯ класса 3. 3. 0 - 1 а 3. 3. 0 - 1 б 3. 3. 0 - 2 18

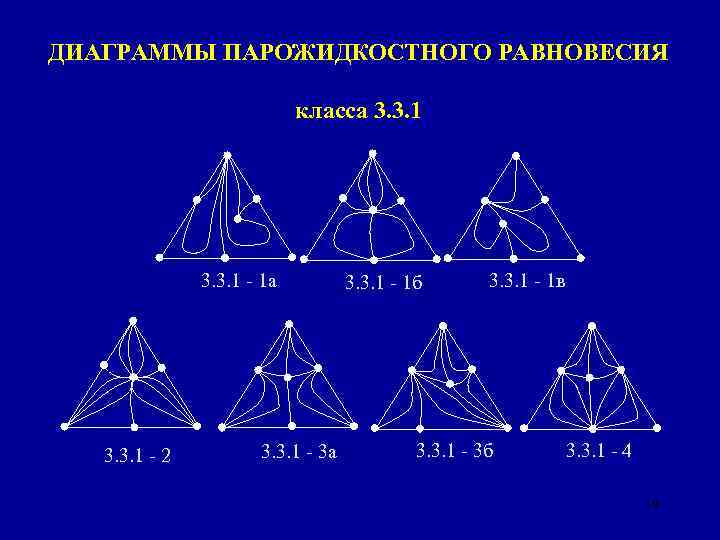ДИАГРАММЫ ПАРОЖИДКОСТНОГО РАВНОВЕСИЯ класса 3. 3. 1 - 1 а 3. 3. 1 - 2 3. 3. 1 - 3 а 3. 3. 1 - 1 б 3. 3. 1 - 1 в 3. 3. 1 - 3 б 3. 3. 1 - 4 19

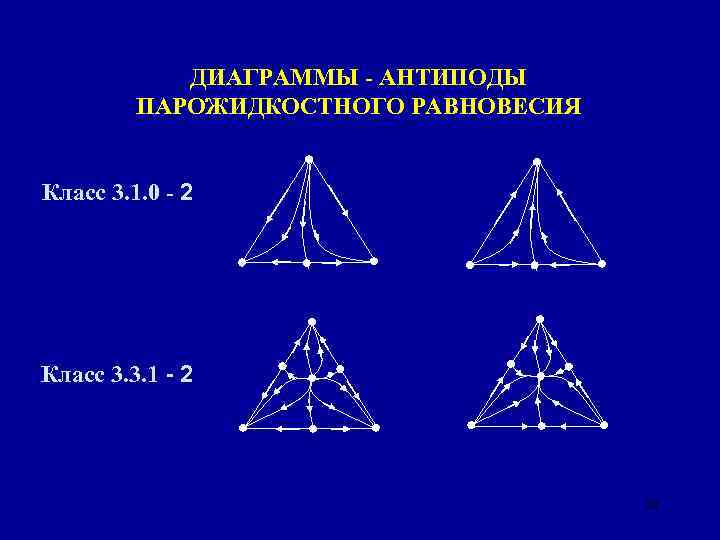ДИАГРАММЫ - АНТИПОДЫ ПАРОЖИДКОСТНОГО РАВНОВЕСИЯ Класс 3. 1. 0 - 2 Класс 3. 3. 1 - 2 20

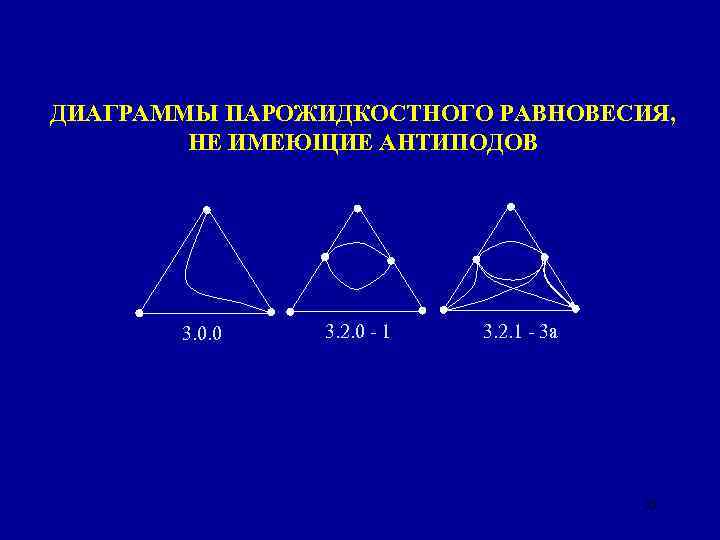ДИАГРАММЫ ПАРОЖИДКОСТНОГО РАВНОВЕСИЯ, НЕ ИМЕЮЩИЕ АНТИПОДОВ 3. 0. 0 3. 2. 0 - 1 3. 2. 1 - 3 а 21

ТЕМА 4 КЛАССИФИКАЦИЯ ДИАГРАММ ФАЗОВОГО РАВНОВЕСИЯ. ТРОЙНЫЕ БИАЗЕОТРОПНЫЕ СИСТЕМЫ ЖИДКОСТЬ – ПАР 22

КЛАССИФИКАЦИЯ ДИАГРАММ ТРЕХКОМПОНЕНТНЫХ БИАЗЕОТРОПНЫХ СИСТЕМ 3. М 2. М 3 Общее количество особых точек равно: М 2 = N 2 + C 2 М 2 = 0; 1; 2; 3; 4; 5; 6 М 3 = N 3 + C 3 М 3= 0; 1; 2 3 = N 1 + C 1 23

ПОДХОД К СОЗДАНИЮ КЛАССИФИКАЦИИ БИАЗЕОТРОПНЫХ СИСТЕМ 24

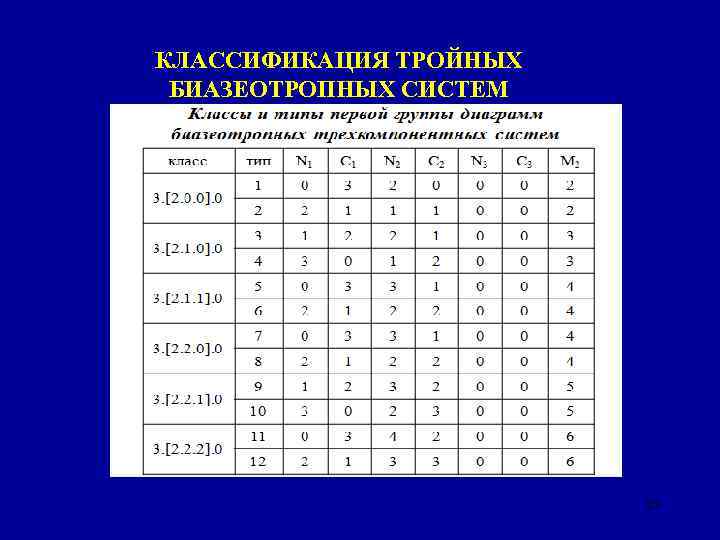КЛАССИФИКАЦИЯ ТРОЙНЫХ БИАЗЕОТРОПНЫХ СИСТЕМ ТАБЛИЦА 25

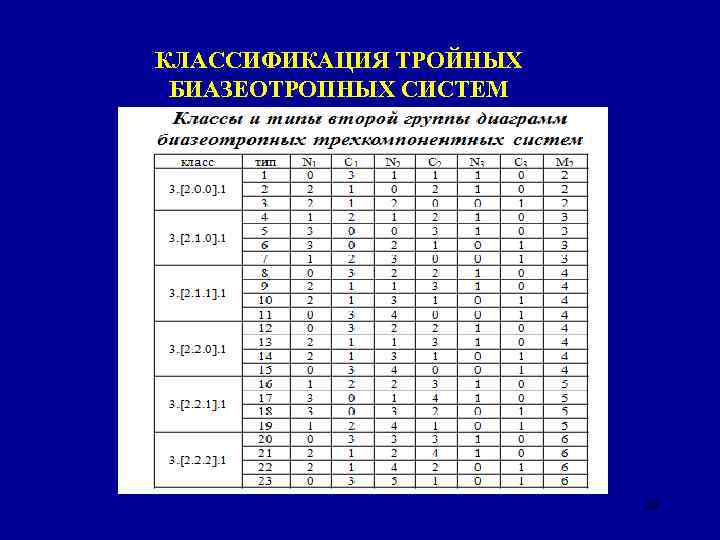КЛАССИФИКАЦИЯ ТРОЙНЫХ БИАЗЕОТРОПНЫХ СИСТЕМ ТАБЛИЦА 26

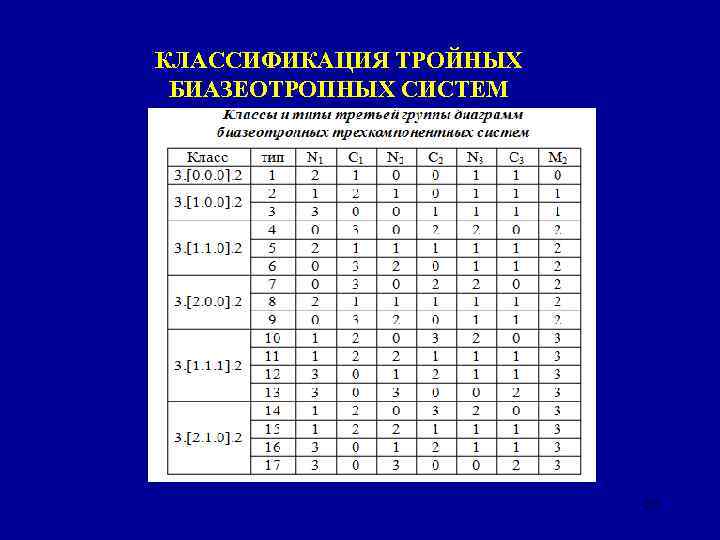КЛАССИФИКАЦИЯ ТРОЙНЫХ БИАЗЕОТРОПНЫХ СИСТЕМ 27

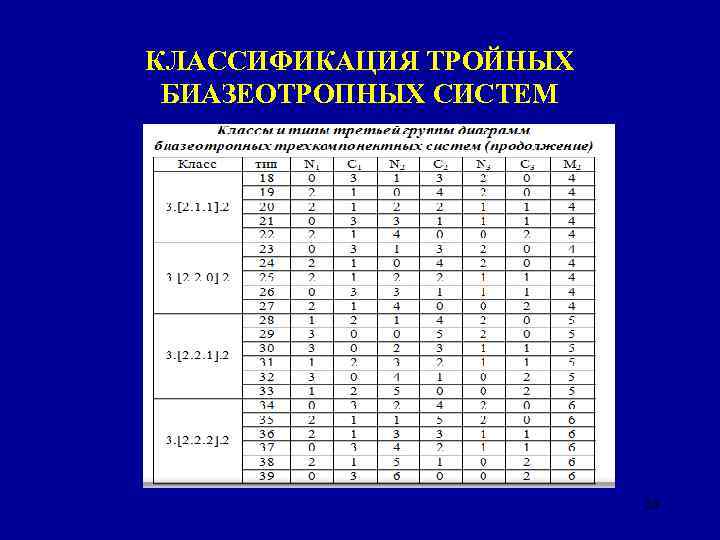КЛАССИФИКАЦИЯ ТРОЙНЫХ БИАЗЕОТРОПНЫХ СИСТЕМ 28

ПРИМЕРЫ ДИАГРАММ КЛАССА 3. [2. 1. 1]. 2. 29

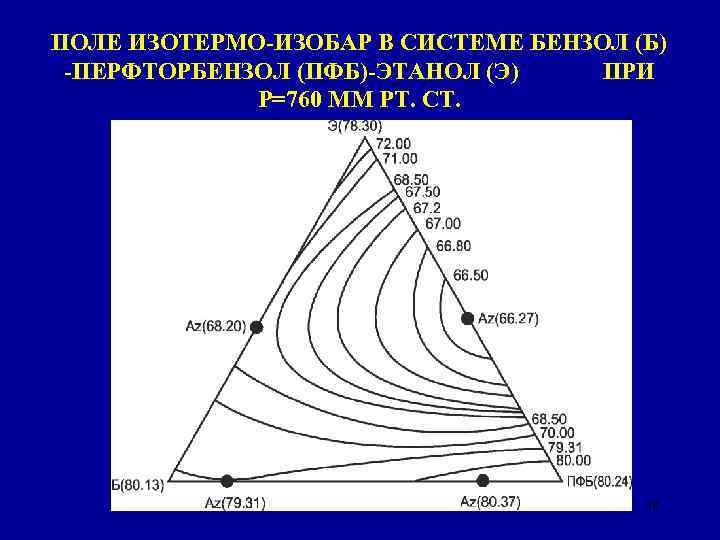ПОЛЕ ИЗОТЕРМО-ИЗОБАР В СИСТЕМЕ БЕНЗОЛ (Б) -ПЕРФТОРБЕНЗОЛ (ПФБ)-ЭТАНОЛ (Э) ПРИ Р=760 ММ РТ. СТ. 30

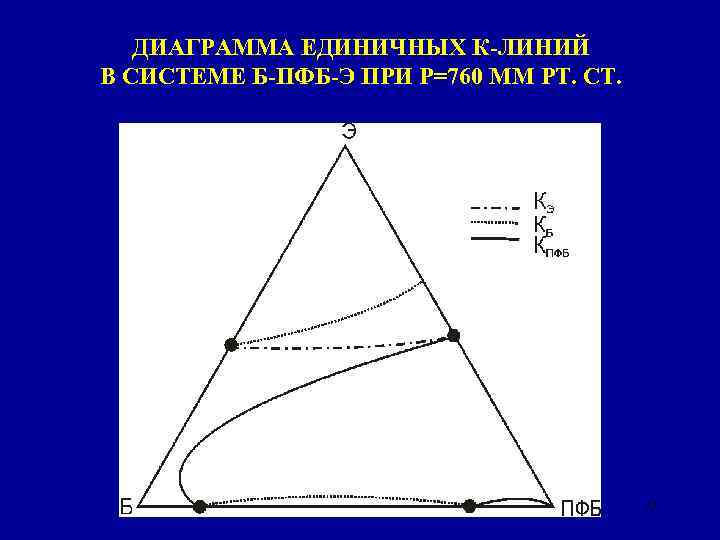ДИАГРАММА ЕДИНИЧНЫХ К-ЛИНИЙ В СИСТЕМЕ Б-ПФБ-Э ПРИ Р=760 ММ РТ. СТ. 31

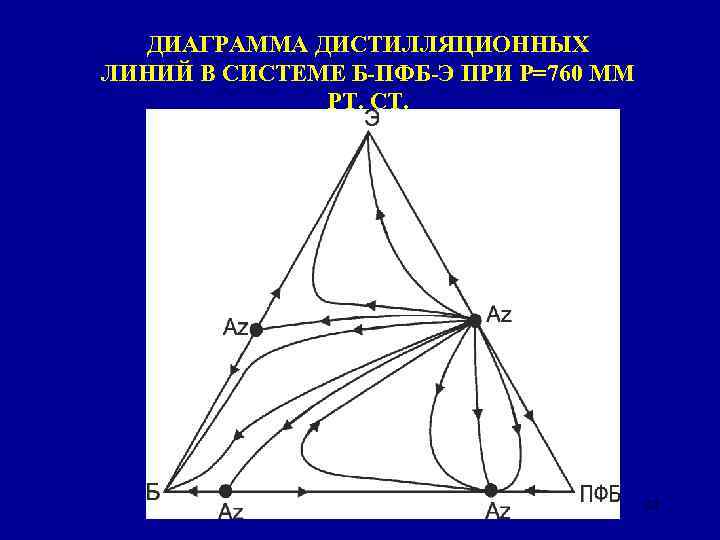ДИАГРАММА ДИСТИЛЛЯЦИОННЫХ ЛИНИЙ В СИСТЕМЕ Б-ПФБ-Э ПРИ Р=760 ММ РТ. СТ. 32

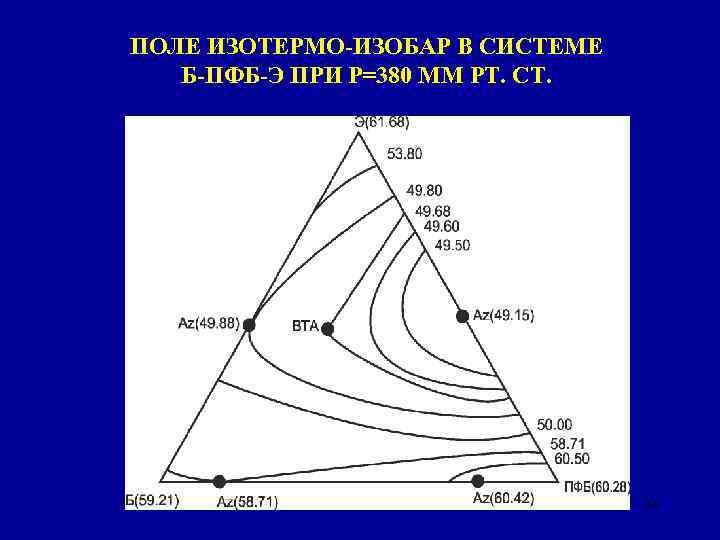ПОЛЕ ИЗОТЕРМО-ИЗОБАР В СИСТЕМЕ Б-ПФБ-Э ПРИ Р=380 ММ РТ. СТ. 33

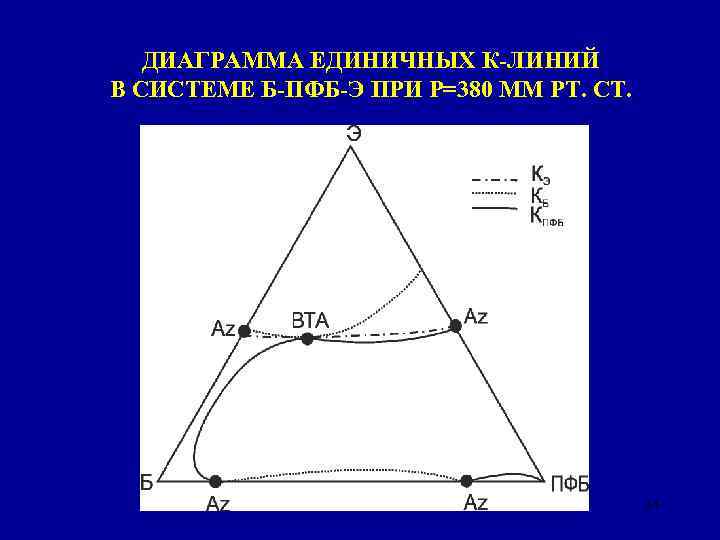ДИАГРАММА ЕДИНИЧНЫХ К-ЛИНИЙ В СИСТЕМЕ Б-ПФБ-Э ПРИ Р=380 ММ РТ. СТ. 34

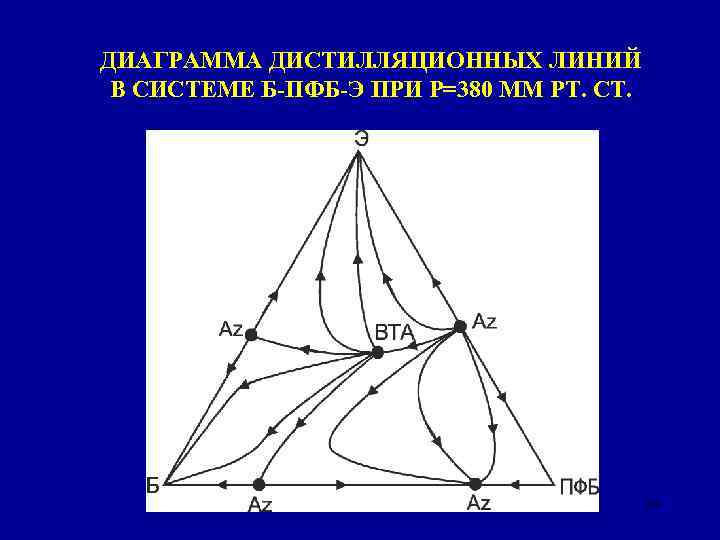ДИАГРАММА ДИСТИЛЛЯЦИОННЫХ ЛИНИЙ В СИСТЕМЕ Б-ПФБ-Э ПРИ Р=380 ММ РТ. СТ. 35

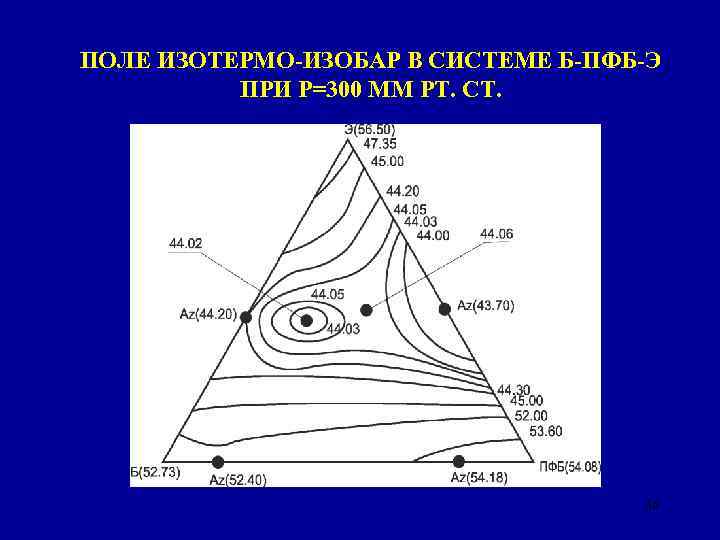ПОЛЕ ИЗОТЕРМО-ИЗОБАР В СИСТЕМЕ Б-ПФБ-Э ПРИ Р=300 ММ РТ. СТ. 36

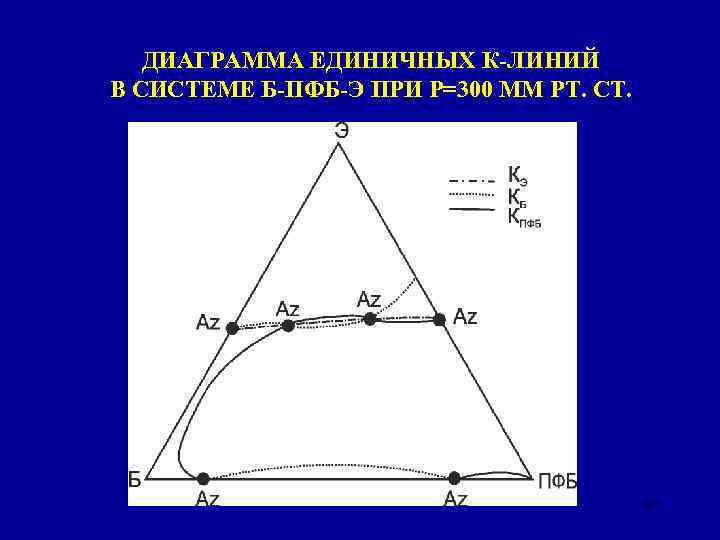ДИАГРАММА ЕДИНИЧНЫХ К-ЛИНИЙ В СИСТЕМЕ Б-ПФБ-Э ПРИ Р=300 ММ РТ. СТ. 37

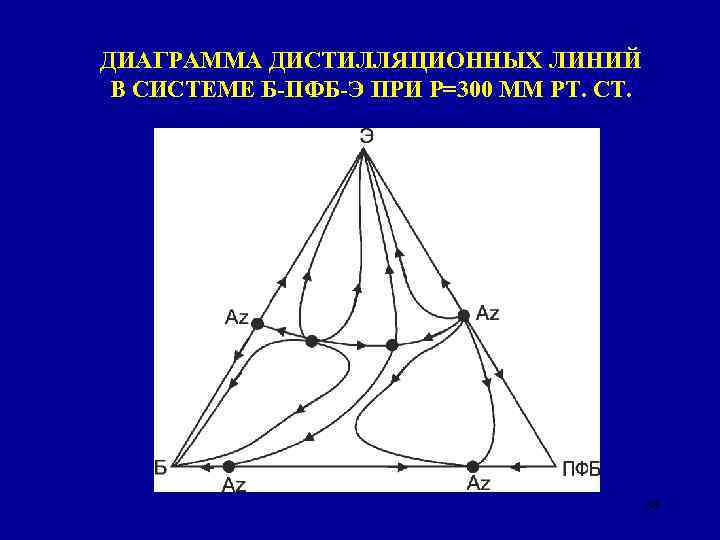ДИАГРАММА ДИСТИЛЛЯЦИОННЫХ ЛИНИЙ В СИСТЕМЕ Б-ПФБ-Э ПРИ Р=300 ММ РТ. СТ. 38

ПРЕОБРАЗОВАНИЕ ДИАГРАММ ИЗОТЕРМО-ИЗОБАР, К- И ДИСТИЛЛЯЦИОННЫХ ЛИНИЙ В СИСТЕМЕ Б-ПФБ-Э 39

ДИАГРАММЫ БИАЗЕОТРОПНЫХ СИСТЕМ ПРИМЕРЫ 40

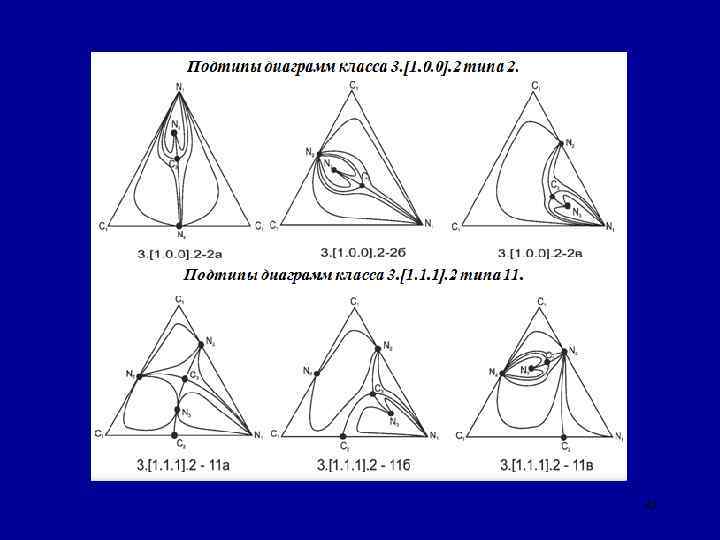41

ТЕМА 4 КЛАССИФИКАЦИЯ ДИАГРАММ ФАЗОВОГО РАВНОВЕСИЯ. ЧЕТЫРЕХКОМПОНЕНТНЫЕ МОНОАЗЕОТРОПНЫЕ СИСТЕМЫ ЖИДКОСТЬ – ПАР 42

ПРИМЕНЕНИЕ ПРАВИЛА АЗЕОТРОПИИ К ФАЗОВЫМ ДИАГРАММАМ ЧЕТЫРЕХКОМПОНЕНТНЫХ СИСТЕМ АЛГОРИТМ АНАЛИЗА ФАЗОВЫХ ДИАГРАММ 1. Построение РАЗВЕРТКИ ТЕТРАЭДРА и выявление сложных особых точек (i=0) 2. Определение типов и индексов простых особых точек на границе тетраэдра (по знакам двух характеристических корней): λ>0 i=+1 Nуст λ <0 i=+1 Nнеуст λ >0 λ <0 i=-1 C 3. Проверка правила азеотропии для границы (развертки) тетраэдра N 3 + N 2 + N 1 -C 3 - C 2 = 2 43

АЛГОРИТМ АНАЛИЗА ФАЗОВЫХ ДИАГРАММ (окончание) 4. Определение типов и индексов особых точек в ТЕТРАЭДРЕ по знакам трех характеристических корнейλ λ>0 i=+1 Nуст λ <0 i=-1 Nнеуст λ >0 λ <0 λ >0 i=+1 C(2) λ >0 λ <0 i=-1 C(1) 5. Проверка правила азеотропии для тетраэдра 3 2(N 4 (+) - N 4 (-) + C 4 (+) - C 4(-)) + Σ (Cг (+) – Cг(-)) = 0 1 6. Определение числа областей дистилляции и выделение сепаратрических многообразий - границ областей дистилляции 44

НЕЛОКАЛЬНЫЕ ЗАКОНОМЕРНОСТИ ФАЗОВЫХ ДИАГРАММ ЧЕТЫРЕХКОМПОНЕНТНЫХ СИСТЕМА 4. 1. 0. 0, ТИП 1 Точка (компонент, Ткип, °С азеотроп) 1 (ацетон) 56, 2 2 (метанол) 64, 7 3 (вода) 100 4 (ЭГ) 197 12 55, 8 Σi 45

НЕЛОКАЛЬНЫЕ ЗАКОНОМЕРНОСТИ ФАЗОВЫХ ДИАГРАММ ЧЕТЫРЕХКОМПОНЕНТНЫХ СИСТЕМА 4. 1. 0. 0, ТИП 1 4 Точка (компонент, азеотроп) 3 Индекс и тип Ткип, °С особой точки отн. развертки 1 1 (ацетон) 56, 2 2 (метанол) 64, 7 3 (вода) 100 4 (ЭГ) 197 12 55, 8 Σi 4 0 (CN 1) +1(N 1 уст) +1(N 1 неуст) 2 4 2 46

НЕЛОКАЛЬНЫЕ ЗАКОНОМЕРНОСТИ ФАЗОВЫХ ДИАГРАММ ЧЕТЫРЕХКОМПОНЕНТНЫХ СИСТЕМА 4. 1. 0. 0, ТИП 1 4 Точка (компонент, азеотроп) 3 4 Индекс и тип особой точки Ткип, °С отн. развертки отн. тетраэдра 1 1 (ацетон) 56, 2 2 (метанол) 64, 7 3 (вода) 100 4 (ЭГ) 197 12 55, 8 Σi 0 (CN 1) +1(N 1 уст) +1(N 2 неуст) 2 +1(N 1 уст) -1(N 1 неуст) 4 4 2 0 1 область дистилляции 1 47 2 3

СИСТЕМА 4. 1. 0. 0, ТИП 2 Точка (компонент, азеотроп) 1 (ацетон) 2 (хлороформ) 3 (бензол) 4 (толуол) 12 Σi Ткип, °С 56, 2 61, 2 80, 1 110, 6 64, 5 48

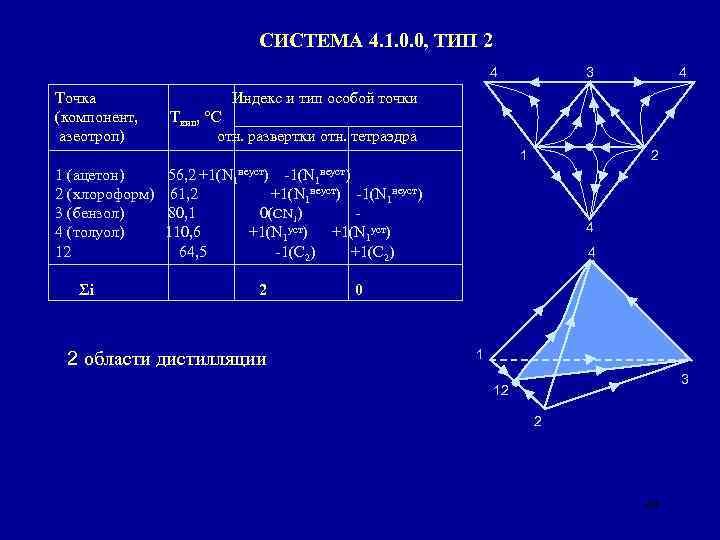СИСТЕМА 4. 1. 0. 0, ТИП 2 4 Точка (компонент, азеотроп) 3 Индекс и тип особой точки Ткип, °С отн. развертки отн. тетраэдра 1 1 (ацетон) 2 (хлороформ) 3 (бензол) 4 (толуол) 12 Σi 4 2 56, 2 +1(N 1 неуст) -1(N 1 неуст) 61, 2 +1(N 1 неуст) -1(N 1 неуст) 80, 1 0(CN 1) 110, 6 +1(N 1 уст) 64, 5 -1(С 2) +1(С 2) 4 4 2 0 2 области дистилляции 1 3 12 2 49

СИСТЕМА 4. 1. 0. 0, ТИП 2 4 Точка (компонент, азеотроп) 3 Индекс и тип особой точки Ткип, °С отн. развертки отн. тетраэдра 1 1 (ацетон) 2 (хлороформ) 3 (бензол) 4 (толуол) 12 Σi 4 2 56, 2 +1(N 1 неуст) -1(N 1 неуст) 61, 2 +1(N 1 неуст) -1(N 1 неуст) 80, 1 0(CN 1) 110, 6 +1(N 1 уст) 64, 5 -1(С 2) +1(С 2) 4 4 2 0 1 2 области дистилляции 4 3 12 2 Сепаратрическое многообразие 3 12 50

СИСТЕМА 4. 3. 1. 0 Точка (компонент, азеотроп) 1 (ацетон) 2 (изопропанол) 3 (дихлорэтан) 4 (вода) 34 23 24 234 Σi Ткип, °С 56, 2 82, 4 83, 7 100 72, 3 72, 7 80, 3 69, 7 51

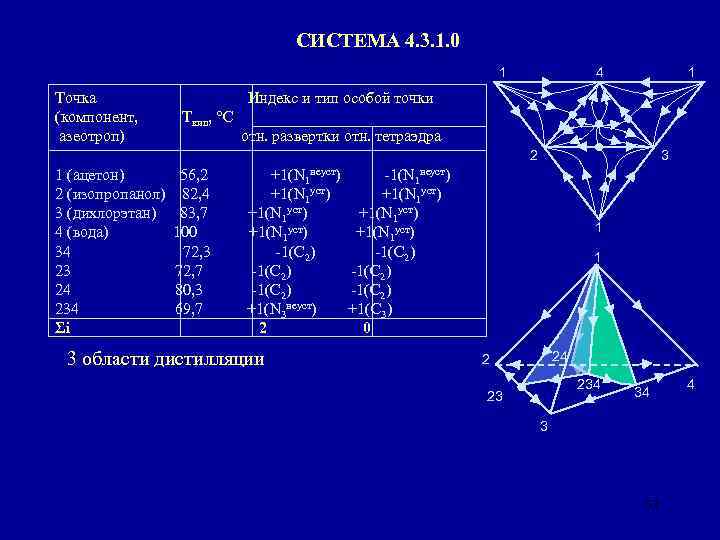СИСТЕМА 4. 3. 1. 0 1 Точка (компонент, азеотроп) 4 1 Индекс и тип особой точки Ткип, °С отн. развертки отн. тетраэдра 2 3 1 (ацетон) 56, 2 +1(N 1 неуст) -1(N 1 неуст) 2 (изопропанол) 82, 4 +1(N 1 уст) 3 (дихлорэтан) 83, 7 +1(N 1 уст) 4 (вода) 100 +1(N 1 уст) 34 72, 3 -1(С 2) 23 72, 7 -1(С 2) 24 80, 3 -1(С 2) 234 69, 7 +1(N 3 неуст) +1(С 3) Σi 2 0 3 области дистилляции 1 1 24 2 234 23 34 3 52 4

СИСТЕМА 4. 3. 1. 0 1 Точка (компонент, азеотроп) 4 1 Индекс и тип особой точки Ткип, °С отн. развертки отн. тетраэдра 2 1 (ацетон) 2 (изопропанол) 3 (дихлорэтан) 4 (вода) 34 23 24 234 Σi 56, 2 82, 4 83, 7 100 72, 3 72, 7 80, 3 69, 7 +1(N 1 неуст) +1(N 1 уст) -1(С 2) +1(N 3 неуст) 2 3 -1(N 1 неуст) +1(N 1 уст) -1(С 2) +1(С 3) 0 3 области дистилляции 1 1 24 2 1 1 234 23 34 3 Сепаратрические многообразия 23 234 24 234 34 53 4

СИСТЕМА 4. 4. 3. 1 Точка (компонент, азеотроп) Ткип, °С 1 (ацетон) 56, 2 2 (хлороформ) 61, 2 3 (этанол) 78, 3 4 (вода) 100 12 64, 5 23 59, 3 24 56, 2 34 78, 0 123 63, 2 124 60, 4 234 55, 3 1234 60, 1 Σi 54

СИСТЕМА 4. 4. 3. 1 Точка (компонент, азеотроп) Индекс и тип Ткип, °С особой точки отн. развертки 1 (ацетон) 56, 2 +1(N 1 неуст) 2 (хлороформ) 61, 2 0 (CN 1) 3 (этанол) 78, 3 +1(N 1 уст) 4 (вода) 100 +1(N 1 уст) 12 64, 5 +1(N 2 уст) 23 59, 3 0(СN 2) 24 56, 2 0(СN 2) 34 78, 0 -1(С 2) 123 63, 2 -1(С 3) 124 60, 4 -1(С 3) 234 55, 3 +1(N 3 неуст) 1234 60, 1 Σi 2 1 3 2 1 4 1 55

СИСТЕМА 4. 4. 3. 1 1 Точка (компонент, азеотроп) 3 1 Индекс и тип особой точки Ткип, °С 1 (ацетон) 56, 2 2 (хлороформ) 61, 2 3 (этанол) 78, 3 4 (вода) 100 12 64, 5 23 59, 3 24 56, 2 34 78, 0 123 63, 2 124 60, 4 234 55, 3 1234 60, 1 Σi отн. развертки отн. тетраэдра +1(N 1 неуст) 0 (CN 1) +1(N 1 уст) +1(N 2 уст) 0(СN 2) -1(С 3) +1(N 3 неуст) 2 -1(N 1 неуст) +1(N 1 уст) +1(N 2 уст) 0 0 -1(С 2) -1(С 3) -1(N 3 неуст) +1(С 4) 0 2 4 1 1 12 2 6 областей дистилляции 24 234 4 34 56 3

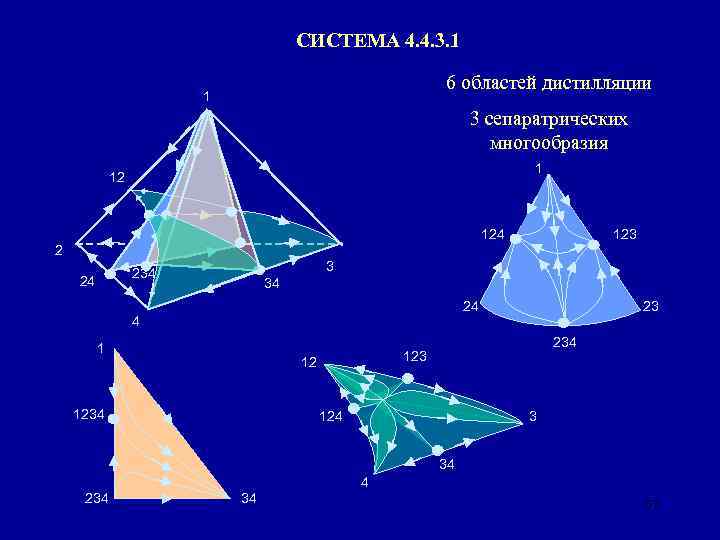СИСТЕМА 4. 4. 3. 1 6 областей дистилляции 1 3 сепаратрических многообразия 1 12 124 2 3 234 24 123 34 23 24 4 1 123 12 1234 124 3 34 4 234 34 57

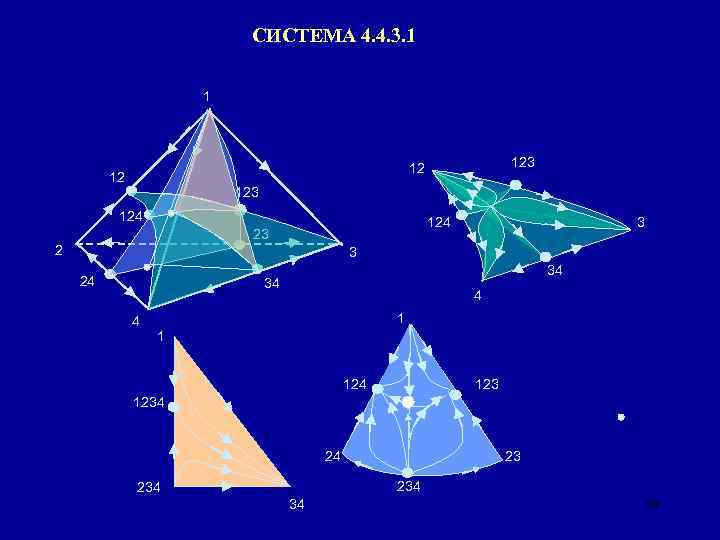СИСТЕМА 4. 4. 3. 1 1 123 12 12 123 124 23 2 3 3 24 34 34 4 4 1 1 124 1234 23 24 234 34 58