Нелинейные уравнения — вводные замечания — метод деления

Нелинейные уравнения - вводные замечания - метод деления отрезка пополам - метод хорд - метод Ньютона (касательных) - метод простой итерации

1 К-тое приближение Условие окончания итераций 2 Практическое условие окончания итераций КР

3. Метод хорд заключается в следующем. Приближенное значение корня уравнения Со находится как точка пересечения оси абсцисс с линией (хордой), соединяющей края нелинейной функции. Далее находят значение функции на краях полученных двух отрезков и на отрезке, где функция меняет знак, продолжают итерации. Приближенное значение корня Со на этапах итерации находят по формуле: F(B 1) < 0 F(B 1)< 0 F(A) > 0 Условие окончания итераций определяется условием малости невязки КР

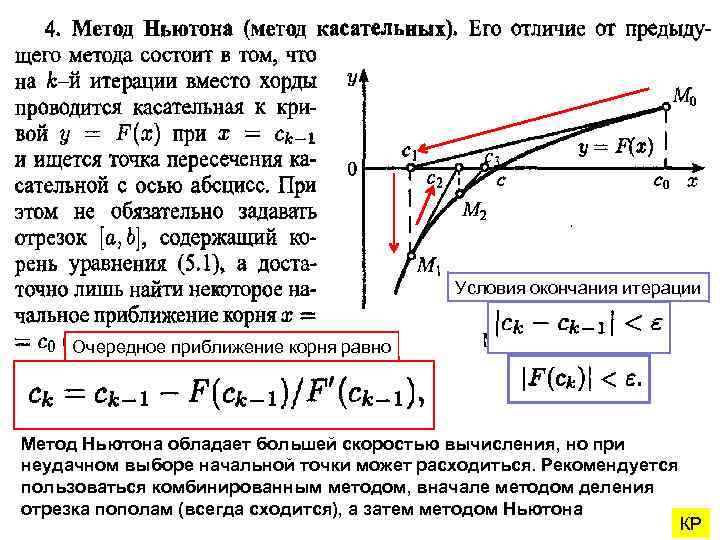Условия окончания итерации Очередное приближение корня равно Метод Ньютона обладает большей скоростью вычисления, но при неудачном выборе начальной точки может расходиться. Рекомендуется пользоваться комбинированным методом, вначале методом деления отрезка пополам (всегда сходится), а затем методом Ньютона КР