НЕЛИНЕЙНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ Общая характеристика нелинейных систем Основная

НЕЛИНЕЙНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ Общая характеристика нелинейных систем Основная особенность нелинейных систем заключается в том, что они не удовлетворяют принципу суперпозиции Модели нелинейных систем в переменных состояния в общем случае это система уравнений

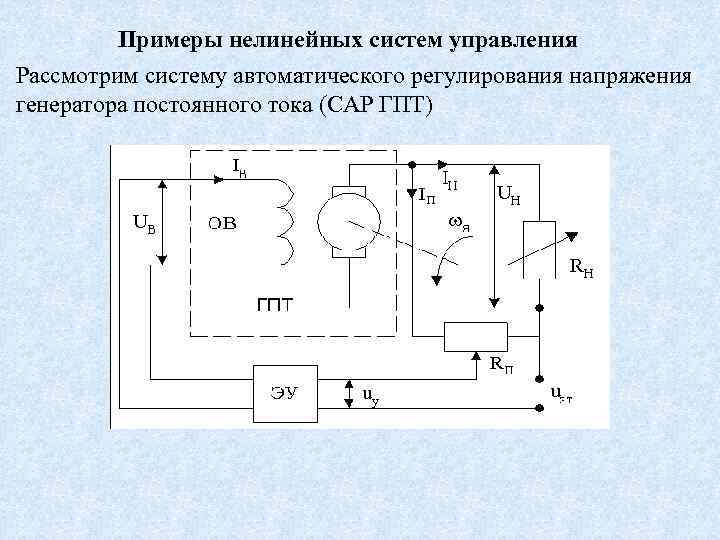
Примеры нелинейных систем управления Рассмотрим систему автоматического регулирования напряжения генератора постоянного тока (САР ГПТ)

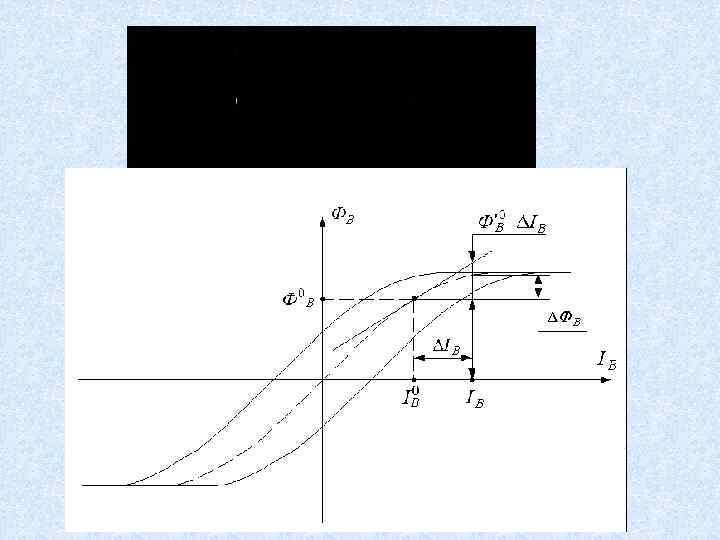
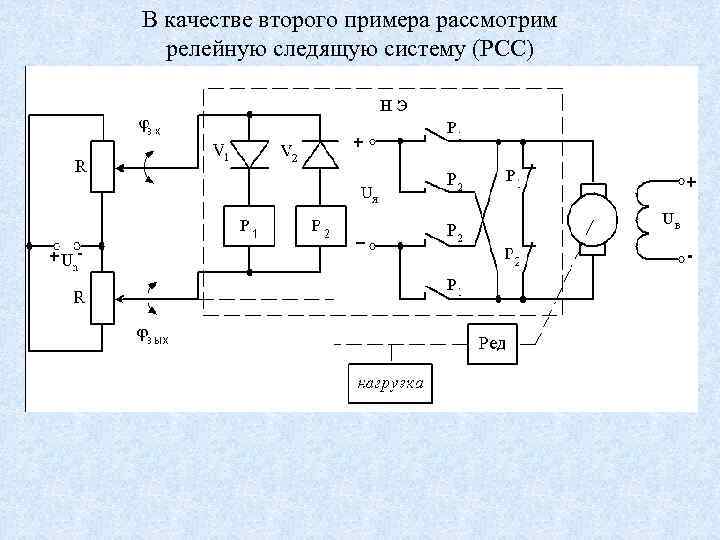
В качестве второго примера рассмотрим релейную следящую систему (РСС)

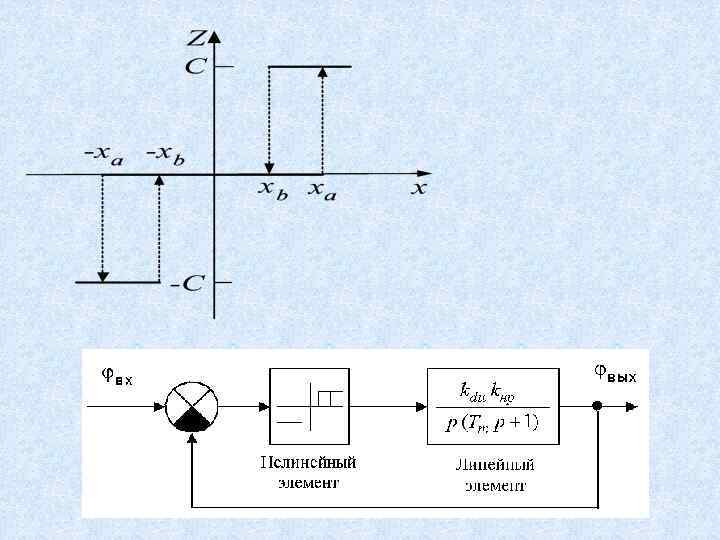
Общие свойства нелинейностей. Типовые звенья В общем случае характеристики нелинейных звеньев могут быть: 1. Симметричными. 2. Непрерывными. 3. Разрывными. 4. Однозначными или многозначными. 5. Обычно , но не всегда

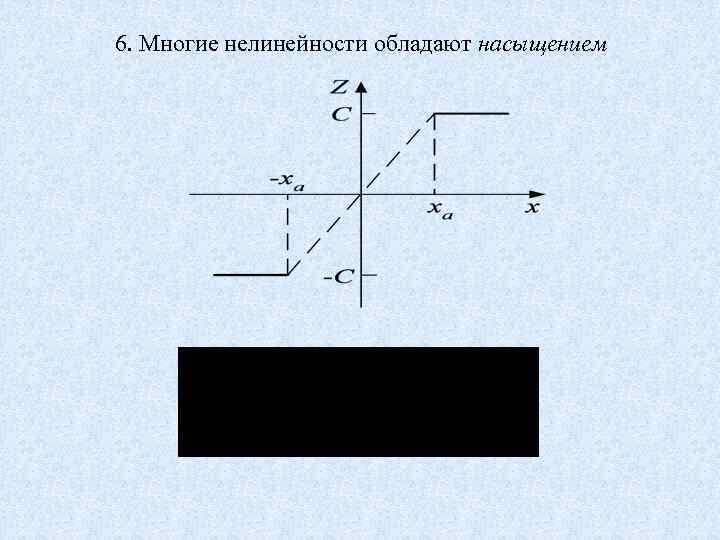
6. Многие нелинейности обладают насыщением

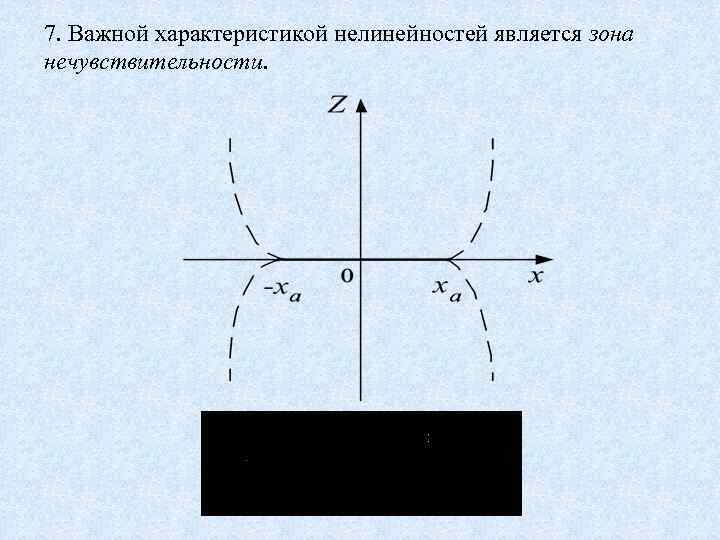
7. Важной характеристикой нелинейностей является зона нечувствительности.

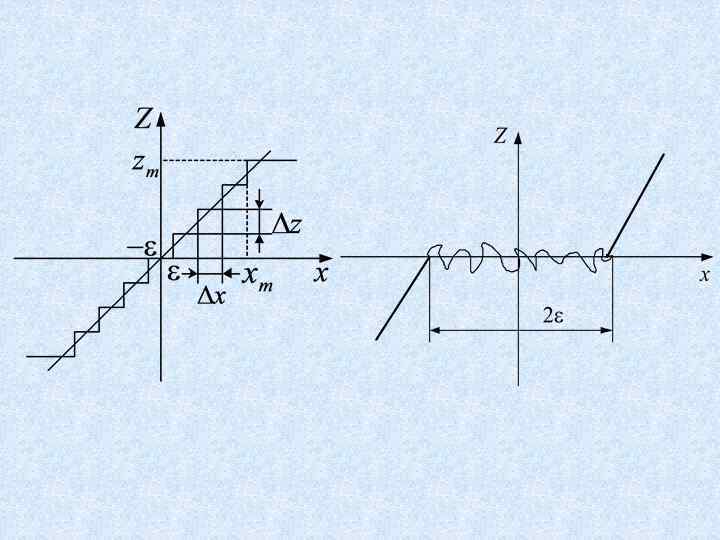
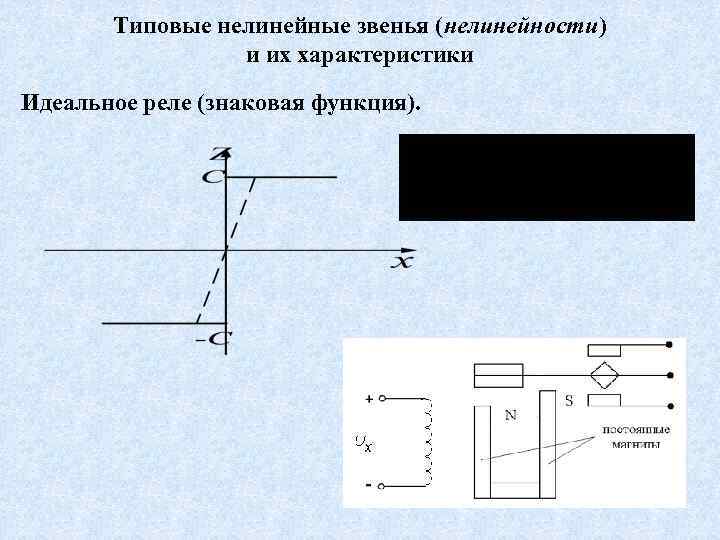
Типовые нелинейные звенья (нелинейности) и их характеристики Идеальное реле (знаковая функция).

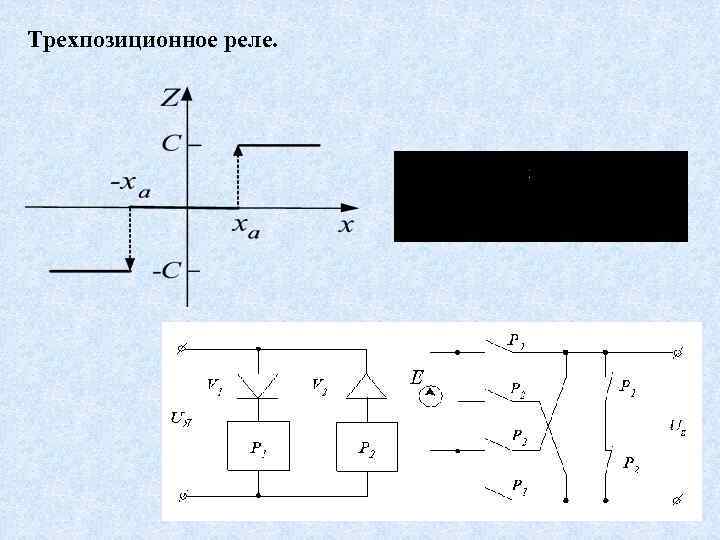
Трехпозиционное реле.

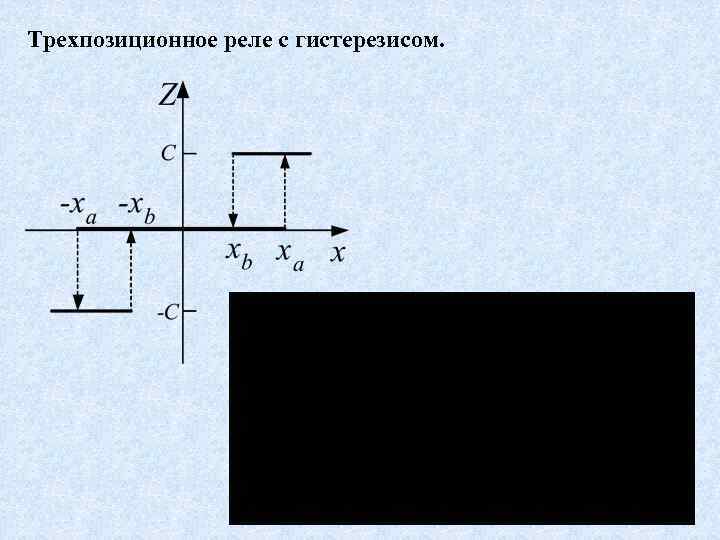
Трехпозиционное реле с гистерезисом.

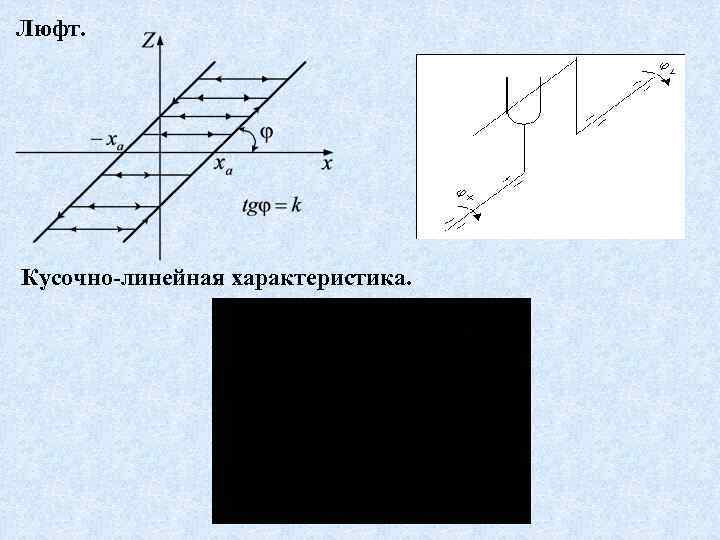
Люфт. Кусочно-линейная характеристика.

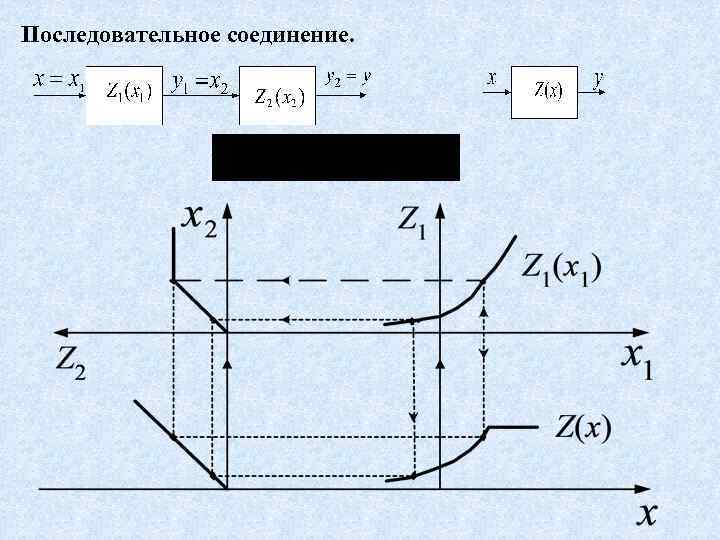
Последовательное соединение.

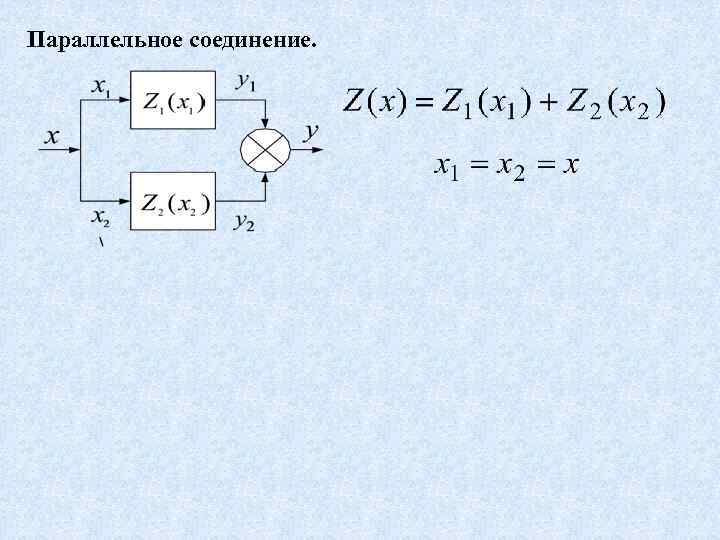
Параллельное соединение.

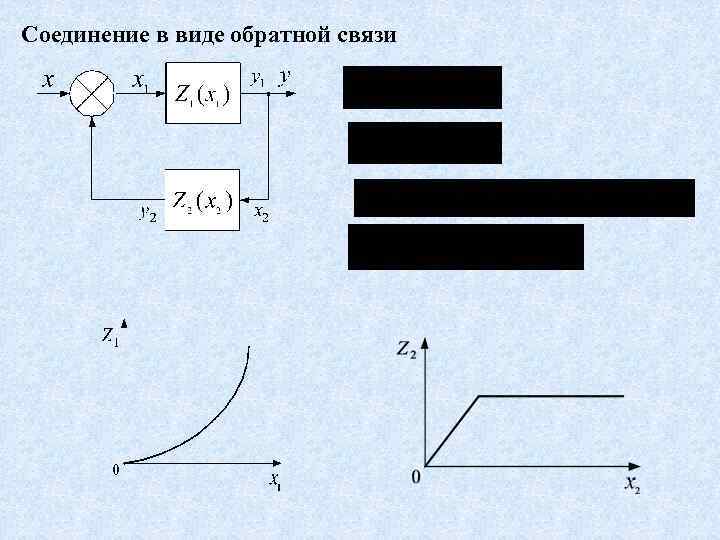
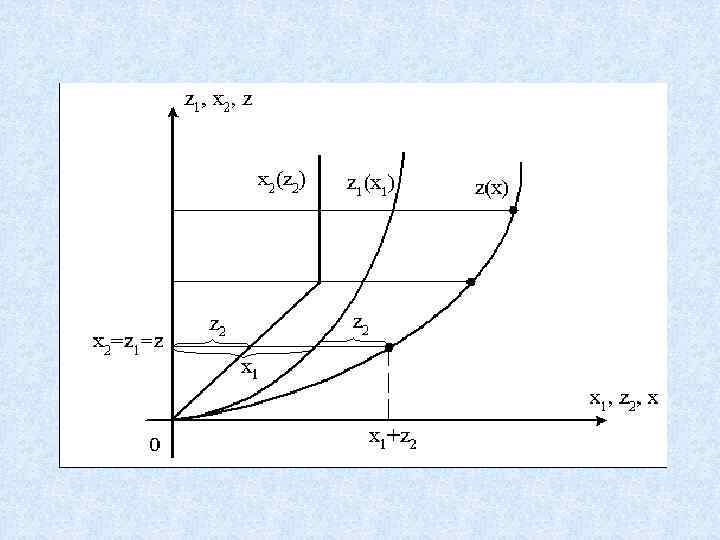
Соединение в виде обратной связи

МЕТОД ФАЗОВОЙ ПЛОСКОСТИ Основные понятия и определения Основное преимущество этого метода – точность и наглядность анализа движений нелинейной системы. Основной недостаток этого метода заключается в том, что он обладает большой эффективностью лишь при исследовании систем второго порядка

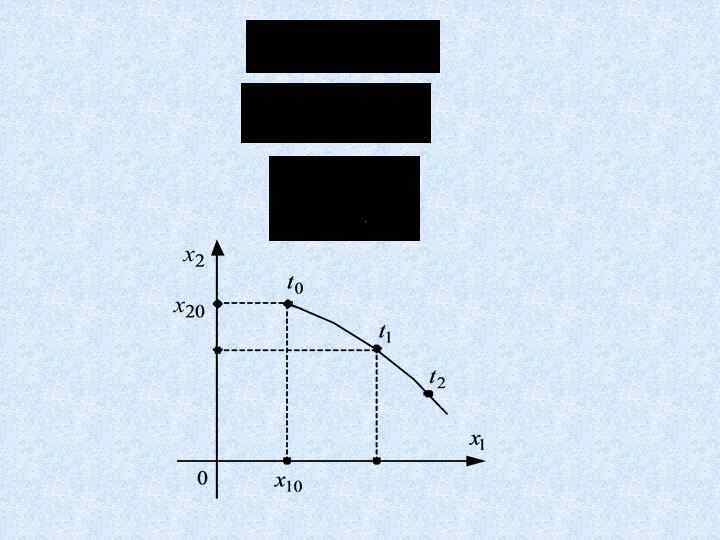
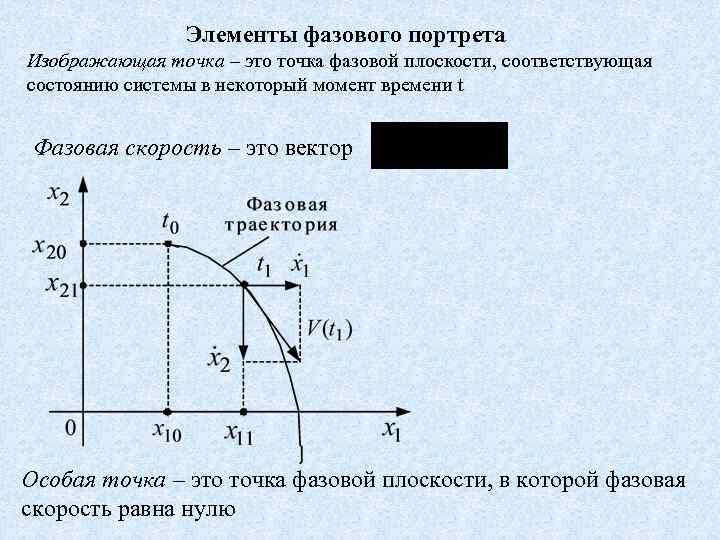
Элементы фазового портрета Изображающая точка – это точка фазовой плоскости, соответствующая состоянию системы в некоторый момент времени t Фазовая скорость – это вектор Особая точка – это точка фазовой плоскости, в которой фазовая скорость равна нулю

Уравнения особых точек Пример Пусть уравнения нелинейной системы имеют вид Найти особые точки

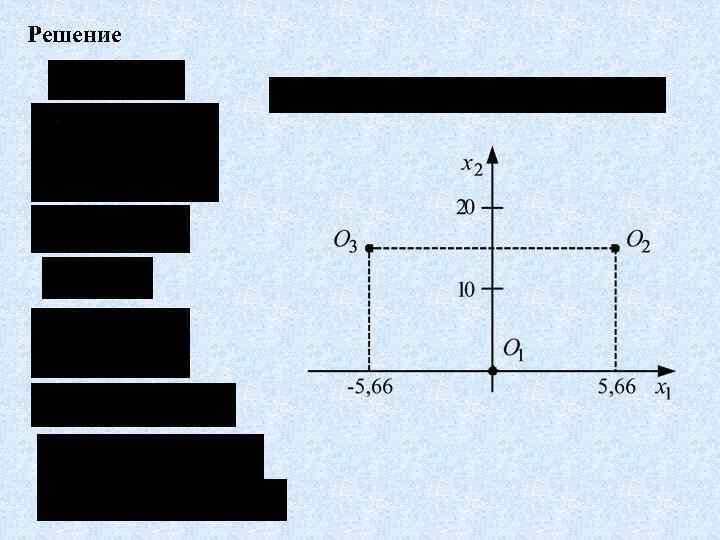
Решение

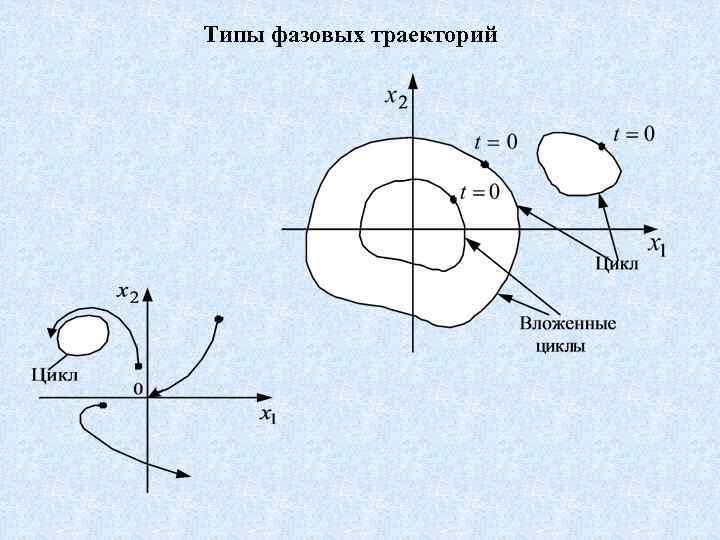
Типы фазовых траекторий

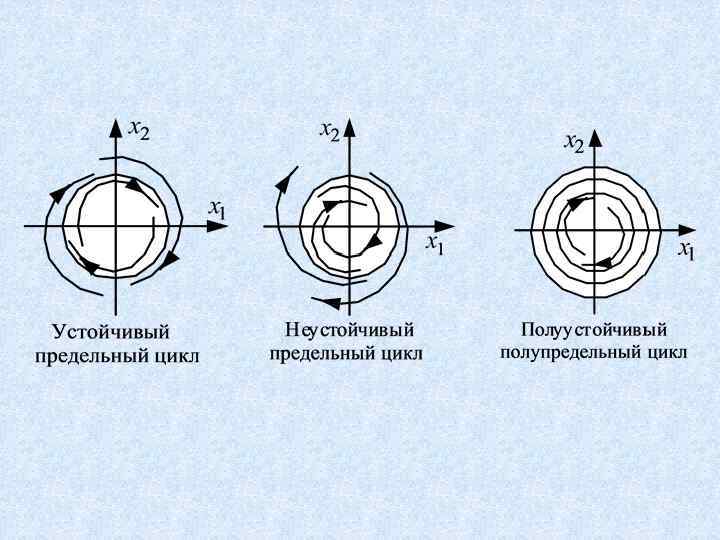
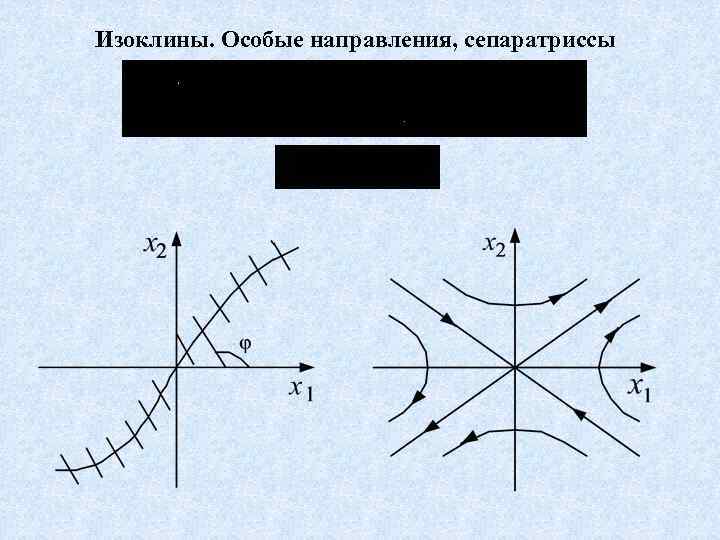
Изоклины. Особые направления, сепаратриссы

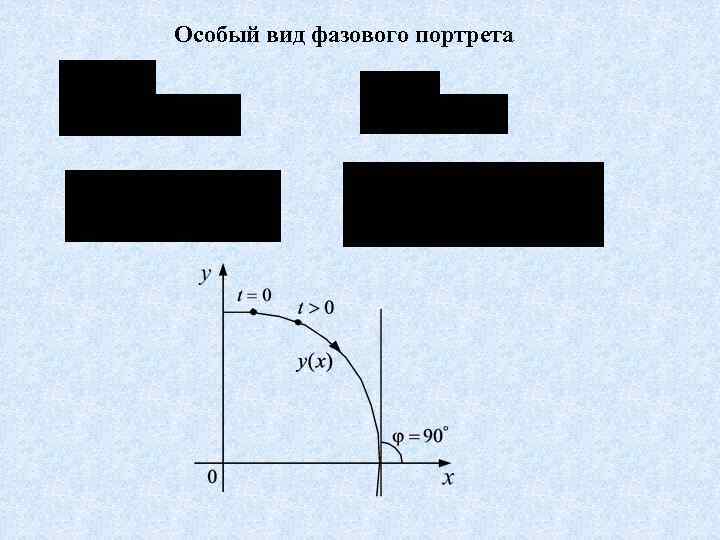
Особый вид фазового портрета

Анализ фазовых траекторий в окрестности особых точек Построение уравнений первого приближения

Пример Найти уравнения первого приближения в окрестности точки Решение

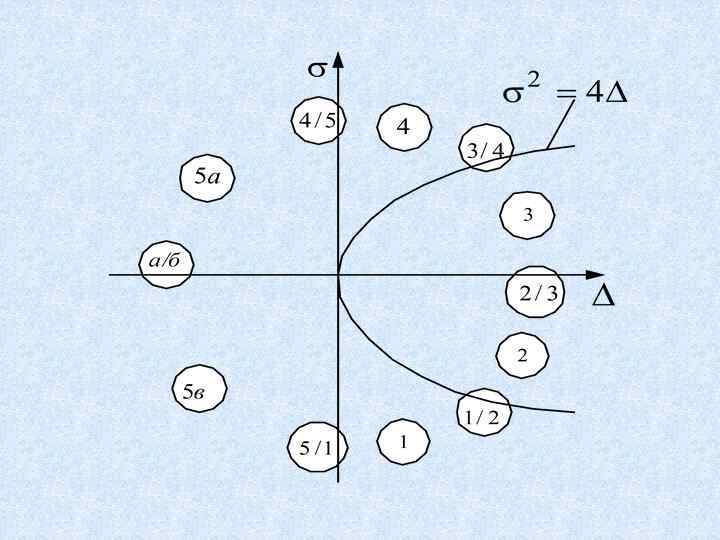
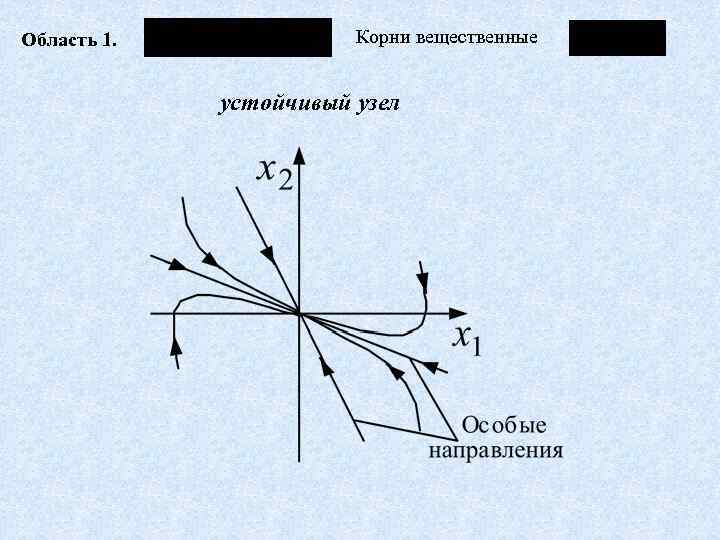
Область 1. Корни вещественные устойчивый узел

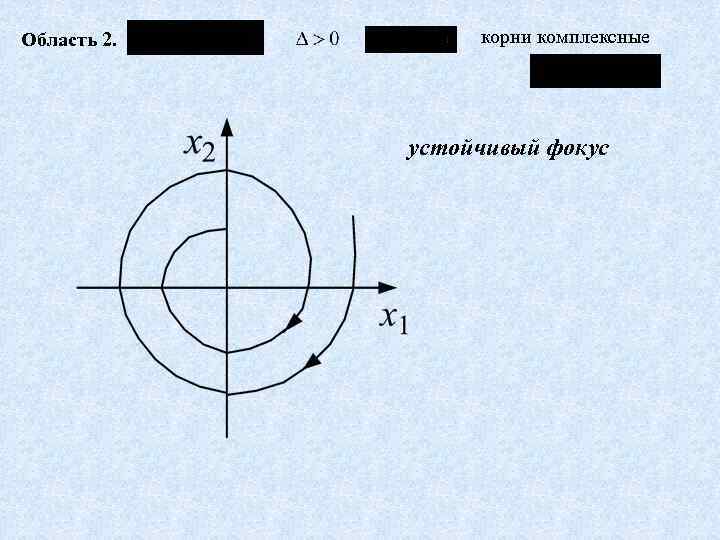
Область 2. корни комплексные устойчивый фокус

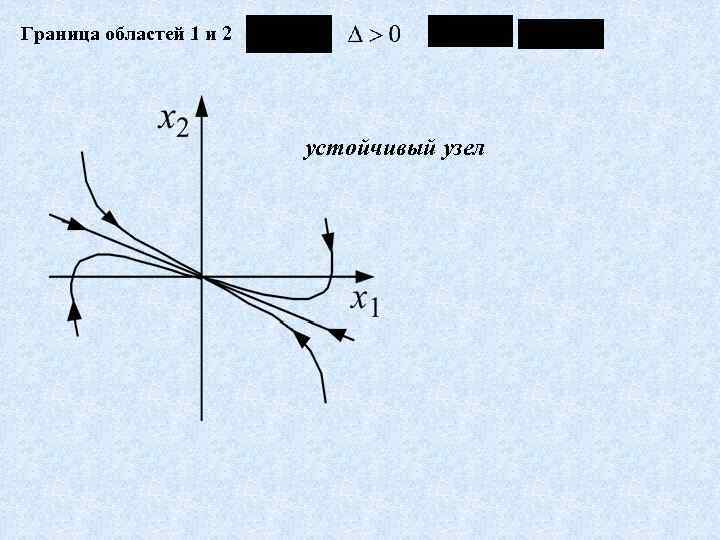
Граница областей 1 и 2 устойчивый узел

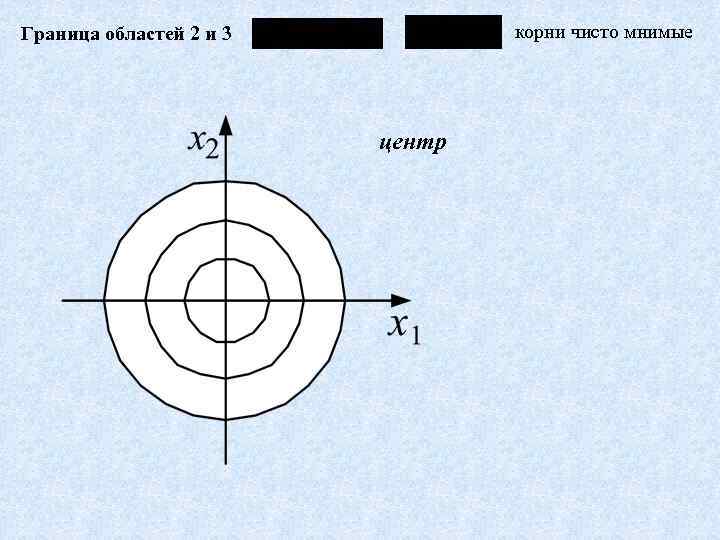
корни чисто мнимые Граница областей 2 и 3 центр

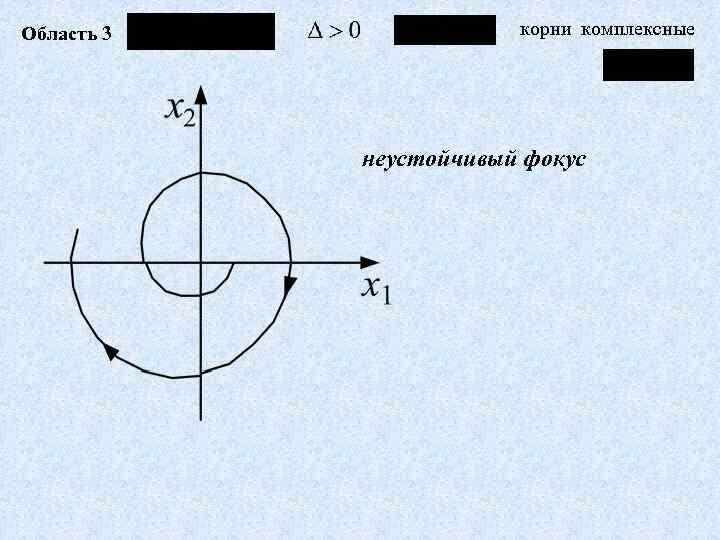
Область 3 корни комплексные неустойчивый фокус

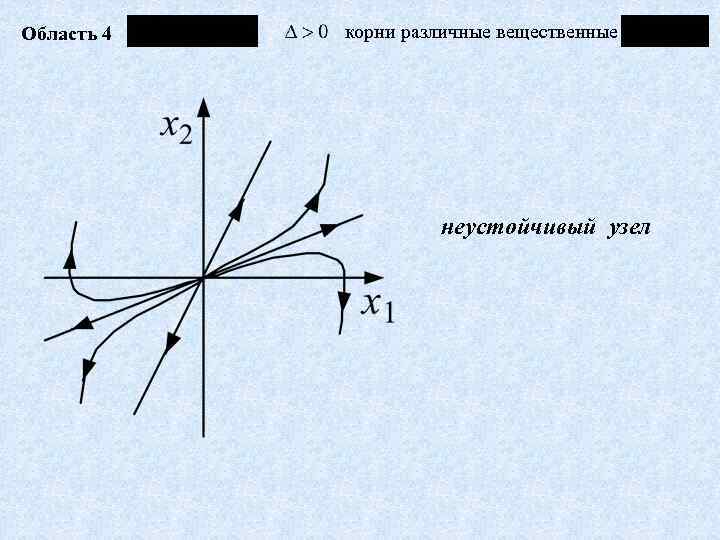
Область 4 корни различные вещественные неустойчивый узел

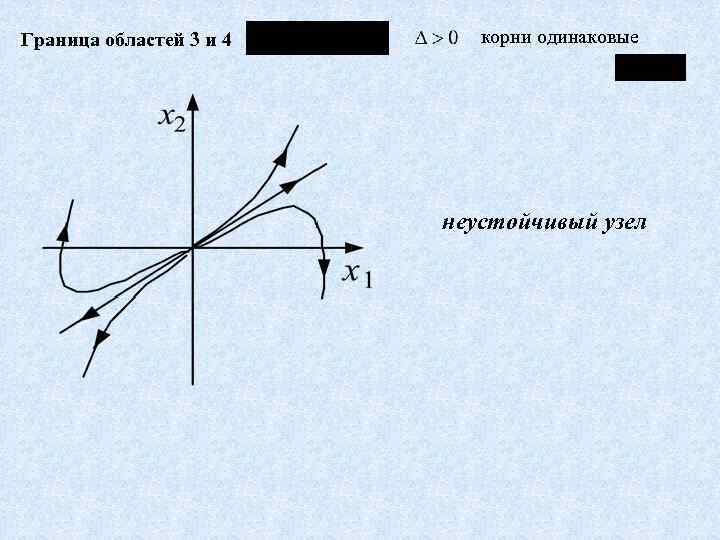
Граница областей 3 и 4 корни одинаковые неустойчивый узел

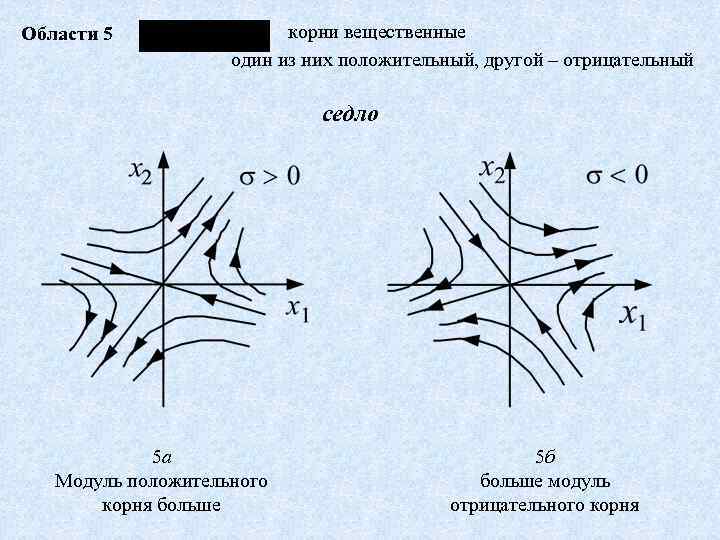
Области 5 корни вещественные один из них положительный, другой – отрицательный седло 5 а Модуль положительного корня больше 5 б больше модуль отрицательного корня

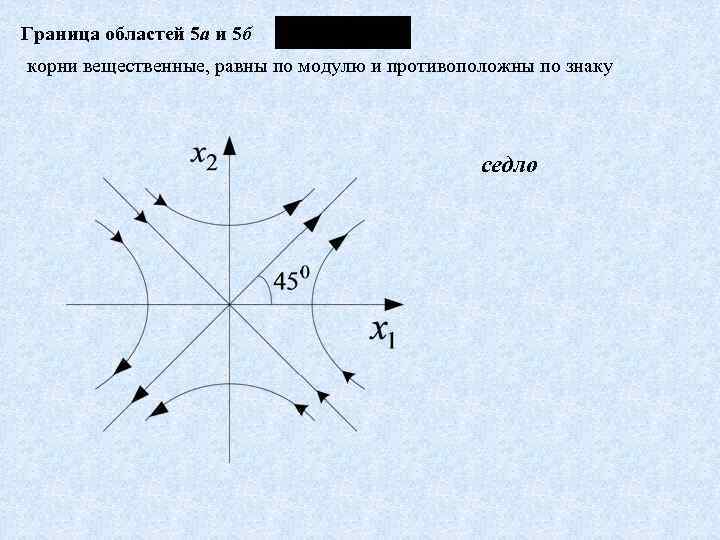
Граница областей 5 а и 5 б корни вещественные, равны по модулю и противоположны по знаку седло

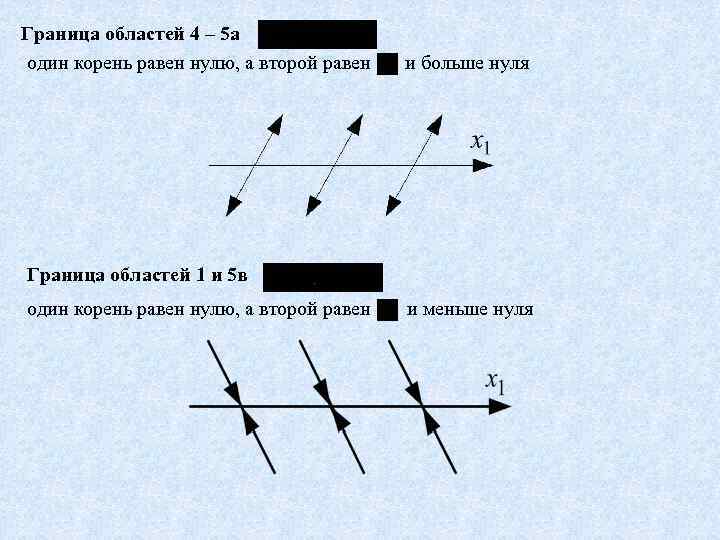
Граница областей 4 – 5 а один корень равен нулю, а второй равен и больше нуля Граница областей 1 и 5 в один корень равен нулю, а второй равен и меньше нуля

Построение фазовых траекторий в большом Метод припасовывания 1. Записать дифференциальные уравнения вход выход системы в изображениях (если система задана структурной схемой). 2. Перейти к уравнениям вход выход в оригиналах. 3. Перейти к уравнениям в переменных состояния (x, y), исключив время и не раскрывая нелинейности. Найти особые точки. 4. На основе условий изменения характера нелинейности сфор мировать уравнения линий переключения, и выделить области фазо вой плоскости, в каждой из которых уравнения фазовых траекторий можно проинтегрировать. Найти выражение для в каждой i й области. 5. Проинтегрировать уравнения фазовых траекторий, и получить алгебраические уравнения фазовых траекторий для каждой i й области. Здесь – постоянные интегрирования.

6. Произвести припасовывание (стыкование) фазовых траекторий путем выбора постоянных интегрирования. При этом начальные условия для последующего участка фазовой траектории будут равны координатам точки пересечения фазовой траектории предыдущего участка и линии переключения. Для аналитического определения этих координат можно решать систему уравнений

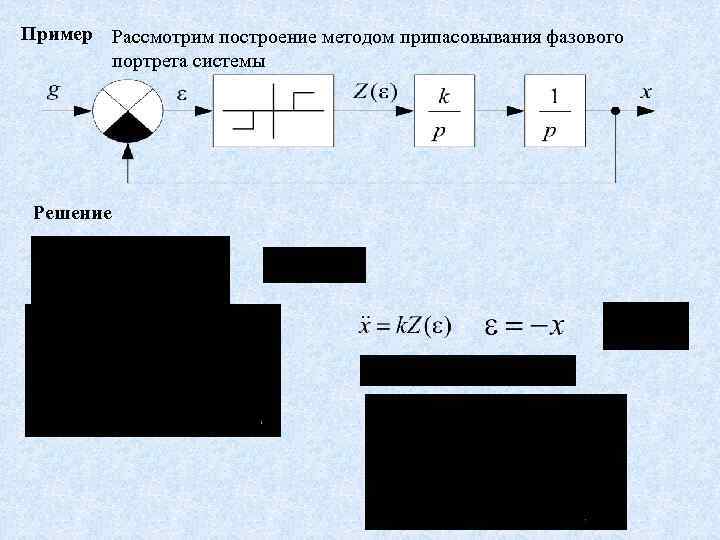
Пример Рассмотрим построение методом припасовывания фазового портрета системы Решение

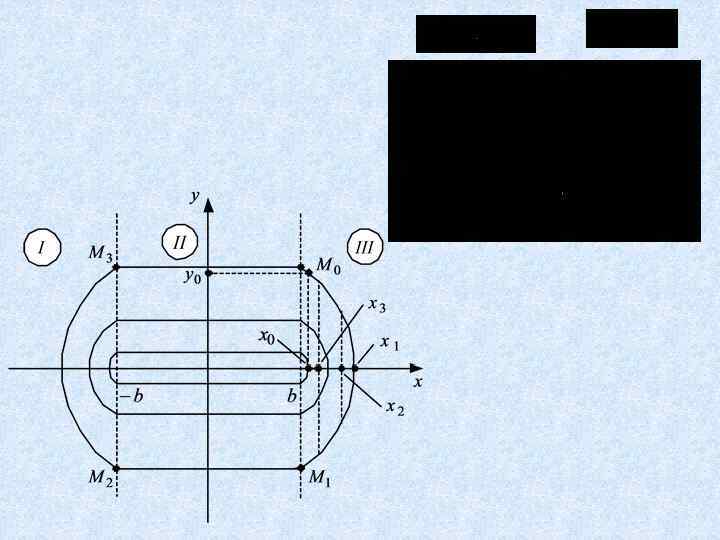
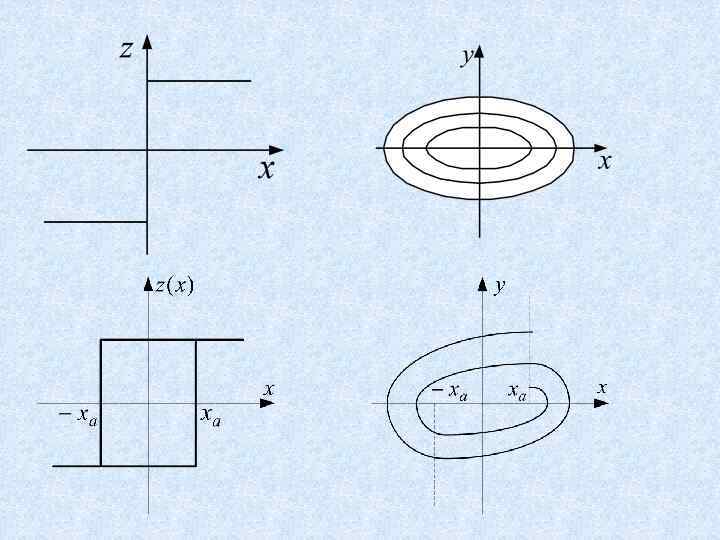
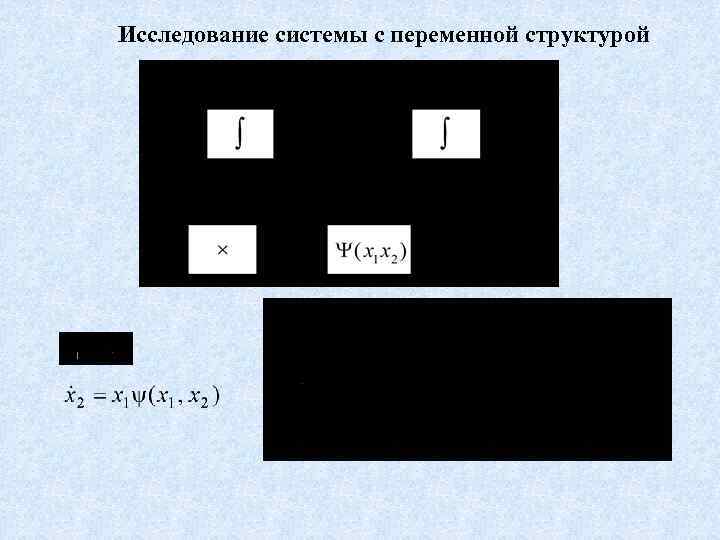
Исследование системы с переменной структурой

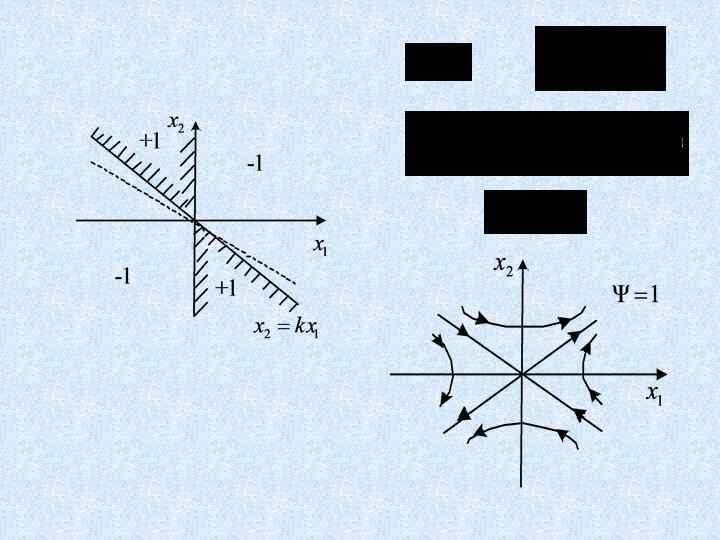
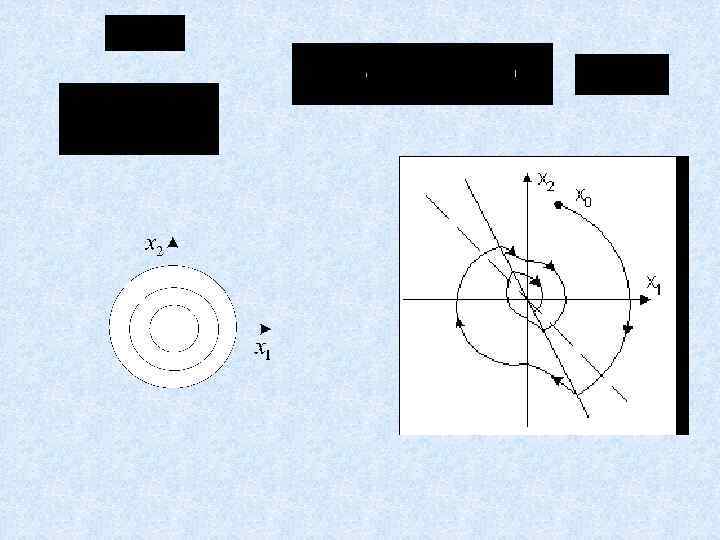
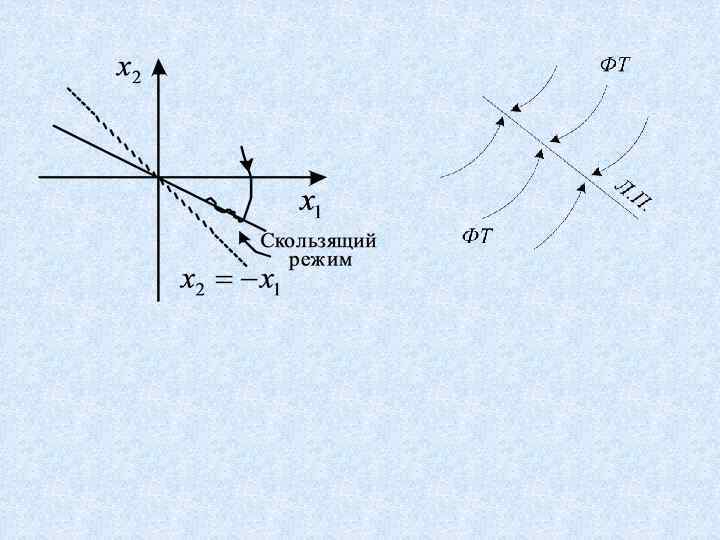
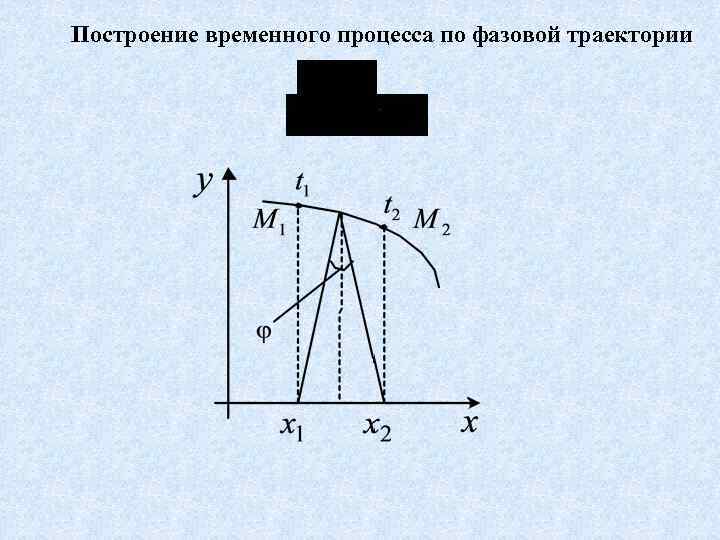
Построение временного процесса по фазовой траектории

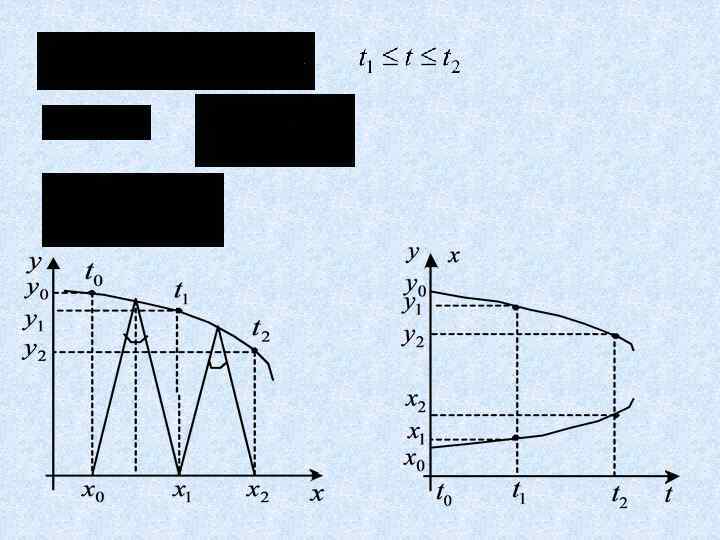
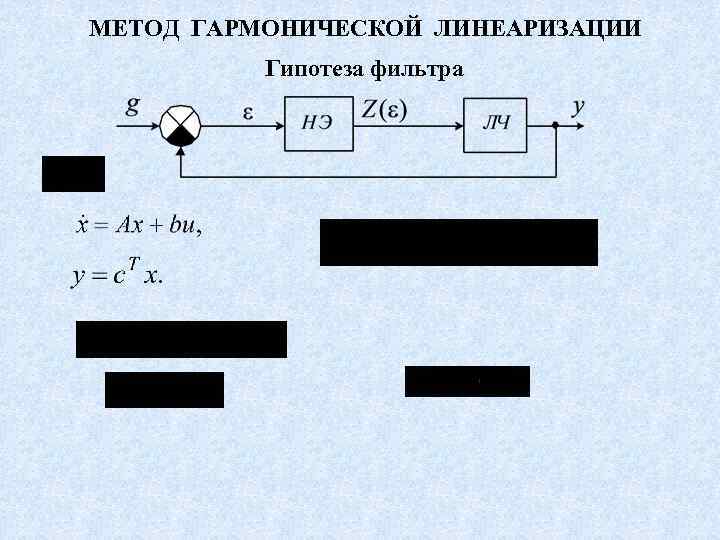
МЕТОД ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ Гипотеза фильтра

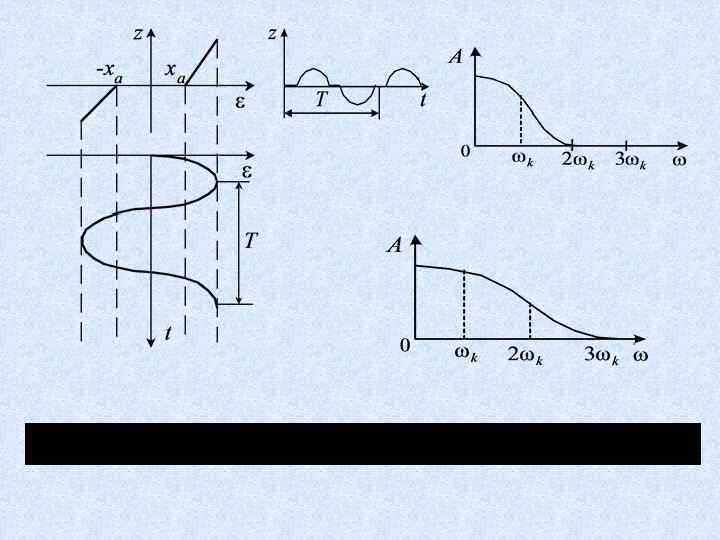
Гармоническая линеаризация

коэффициентом гармонической линеаризации вещественные и мнимые коэффициенты гармонической линеаризации

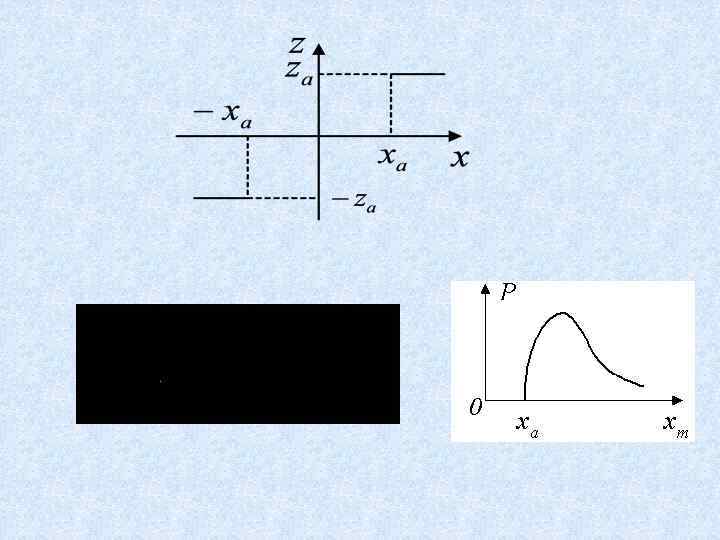
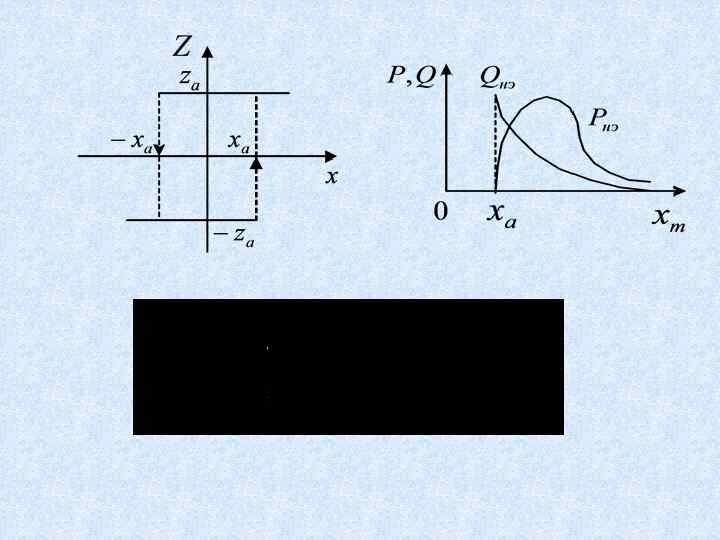
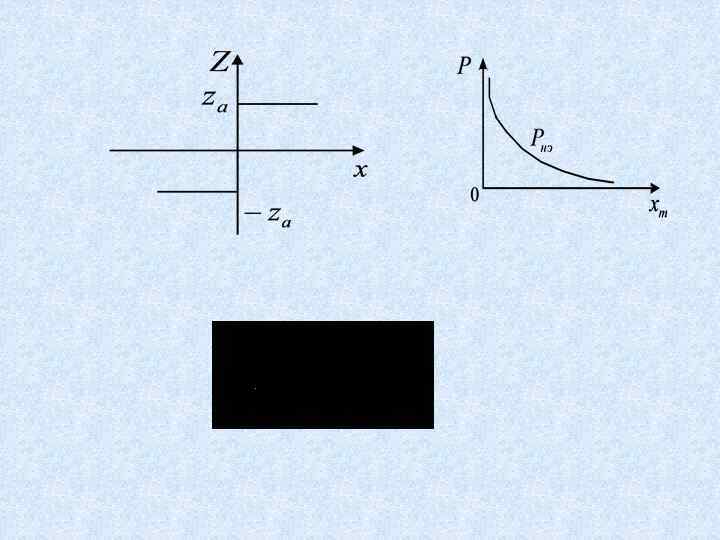
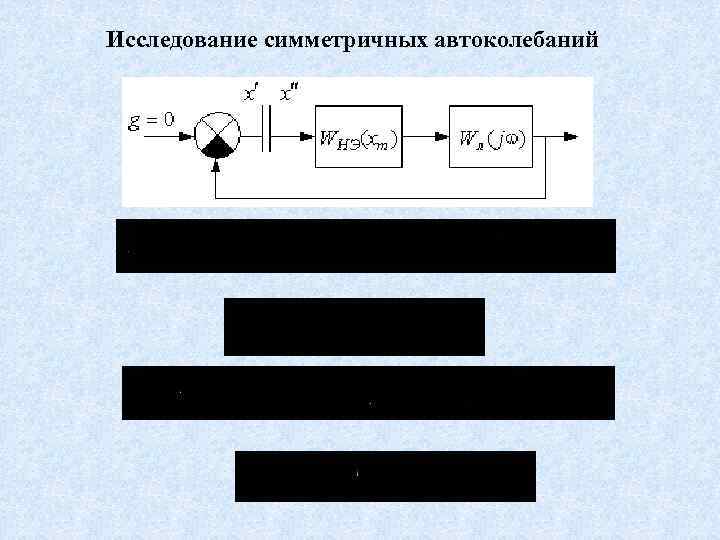
Исследование симметричных автоколебаний

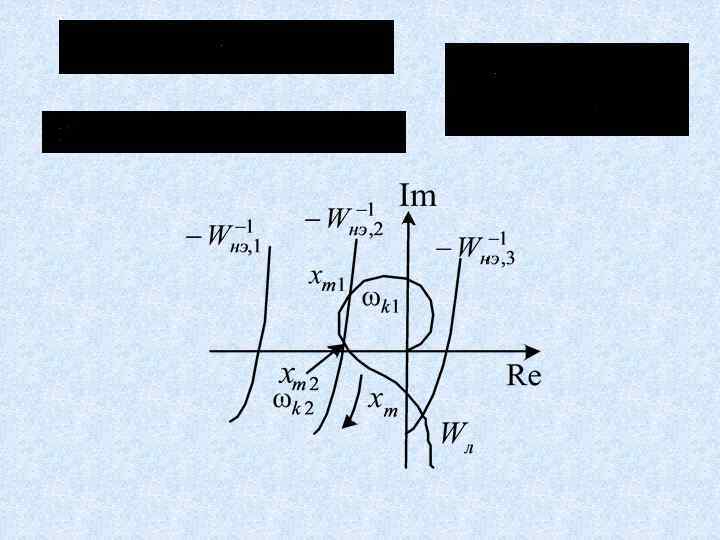
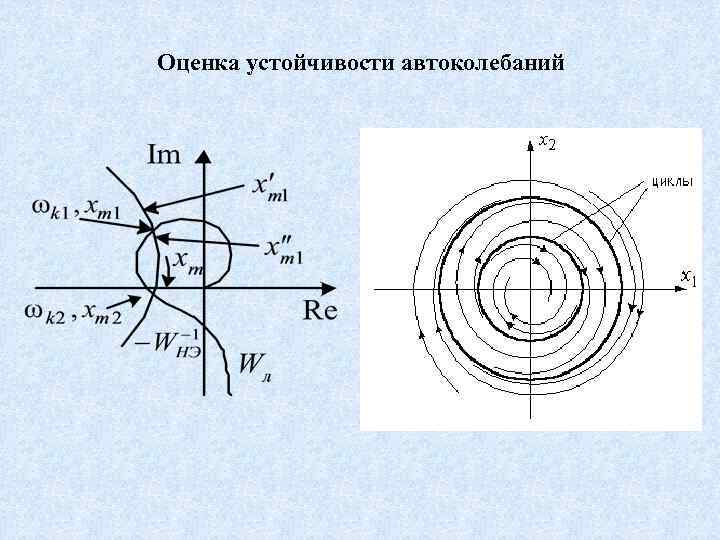
Оценка устойчивости автоколебаний

Критерий устойчивости автоколебаний. Если при увеличении амплитуды колебаний годограф нелинейного элемента пересекает годограф линейной части извне вовнутрь, то точке пересечения соответствуют неустойчивые автоколебания, если же – изнутри вовне, то – устойчивые автоколебания Проверка гипотезы фильтра Пример Проверить возможность существования автоколебаний в системе

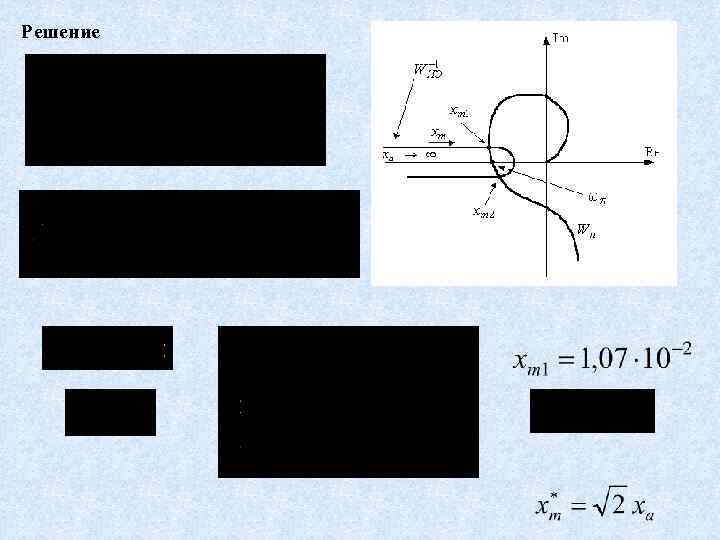
Решение

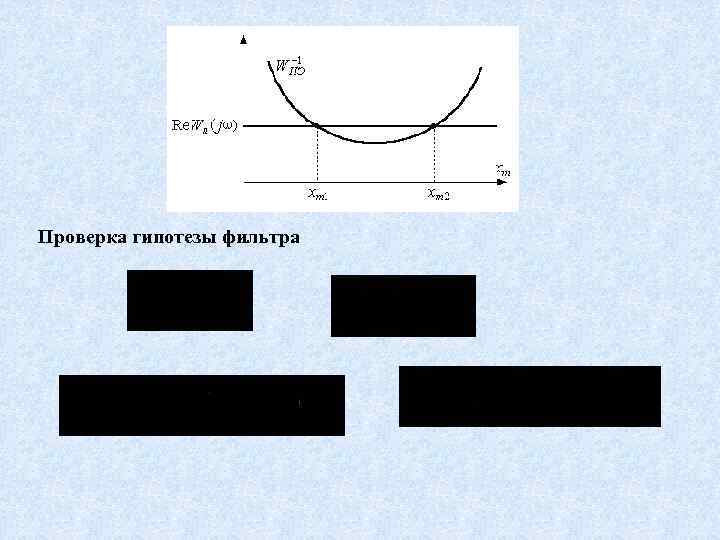
Проверка гипотезы фильтра

Пример Найти ошибку обусловленную автоколебаниями, возникающими в системе, рассмотренной выше Решение

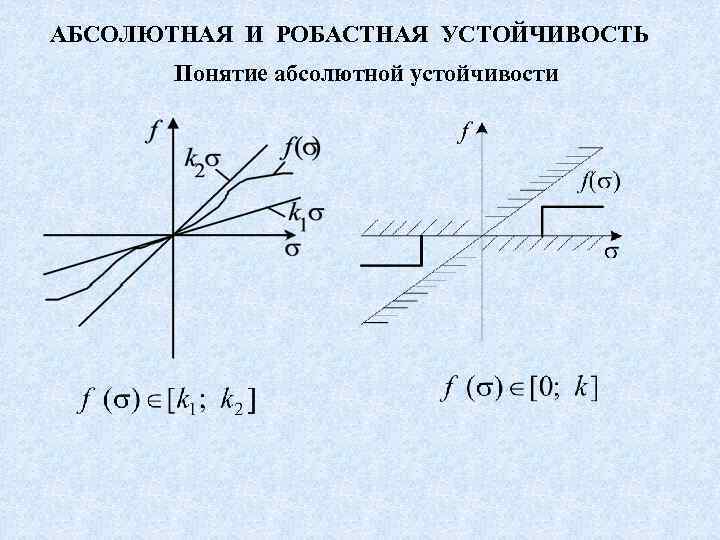
АБСОЛЮТНАЯ И РОБАСТНАЯ УСТОЙЧИВОСТЬ Понятие абсолютной устойчивости

Определение. Система называется абсолютно ус тойчивой если её , единственное положение равновесия асимптотически устойчиво в целом при любой нели нейности из заданного класса

Критерий абсолютной устойчивости Попова а) б) в) линейная система, полученная из нелинейной при замене на устойчива асимптотически

Критерий Попова. Нелинейная система, показанная на рис. 12. 3, является абсолютно устойчивой, если выполнены указанные выше условия а) – в), [0, ] выполняется неравенство и при всех Геометрическая форма критерия Попова

Графический вариант критерия Попова

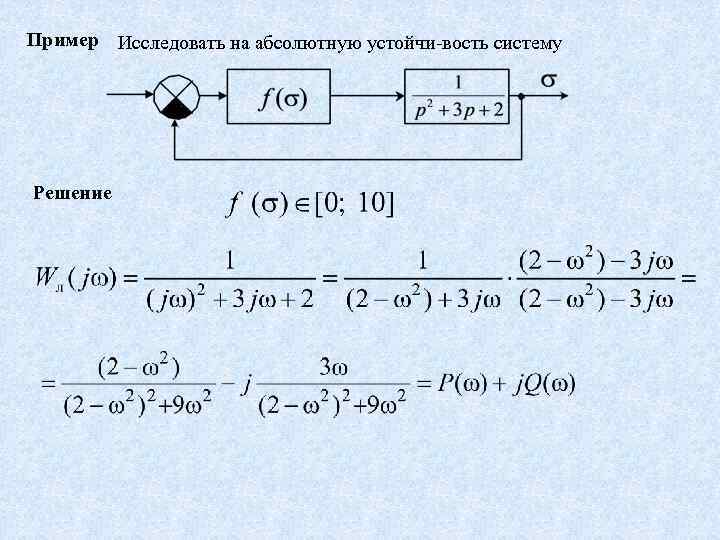
Пример Исследовать на абсолютную устойчи вость систему Решение

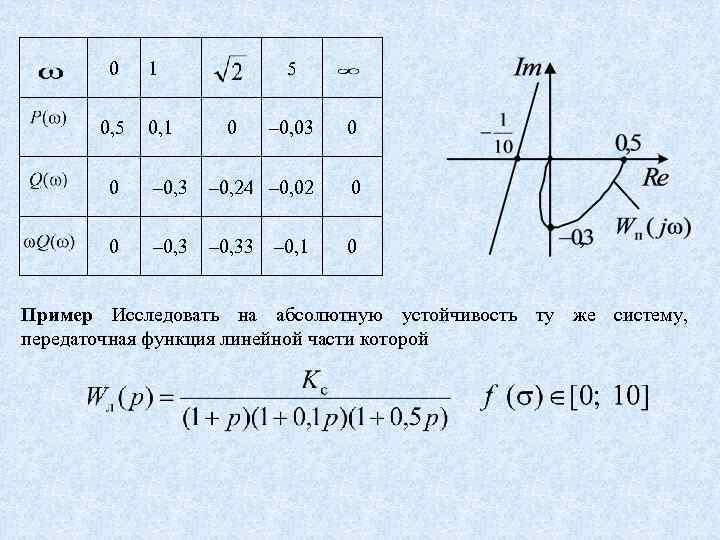
0 0, 5 1 0, 1 5 0 – 0, 03 0 0 – 0, 3 – 0, 24 – 0, 02 0 0 – 0, 33 0 – 0, 1 Пример Исследовать на абсолютную устойчивость ту же систему, передаточная функция линейной части которой

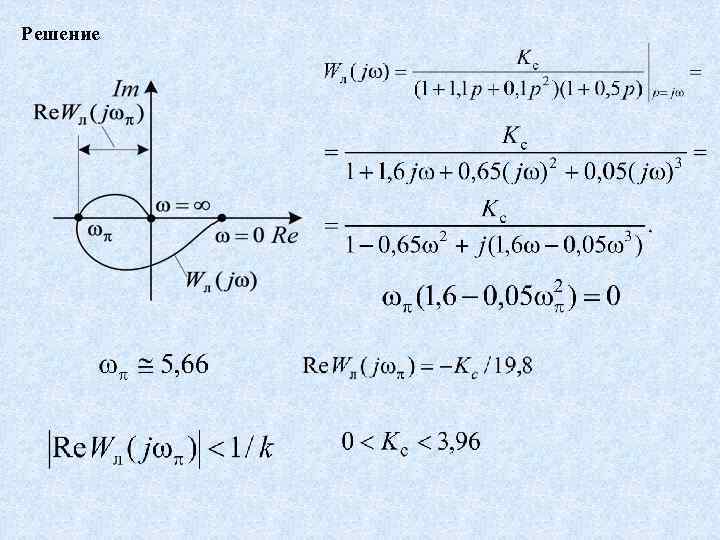
Решение

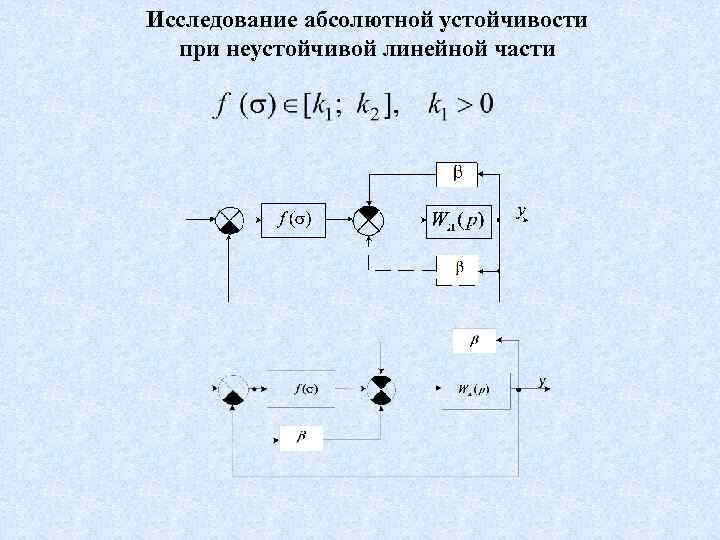
Исследование абсолютной устойчивости при неустойчивой линейной части

Круговой критерий Воронова Определение. Если выполняются условия а), б) и неравенство то нелинейная система абсолютно устойчива

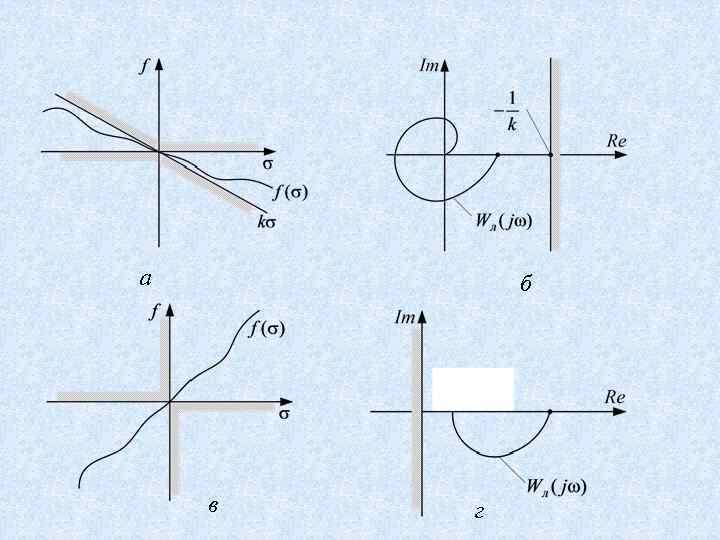
а б в г

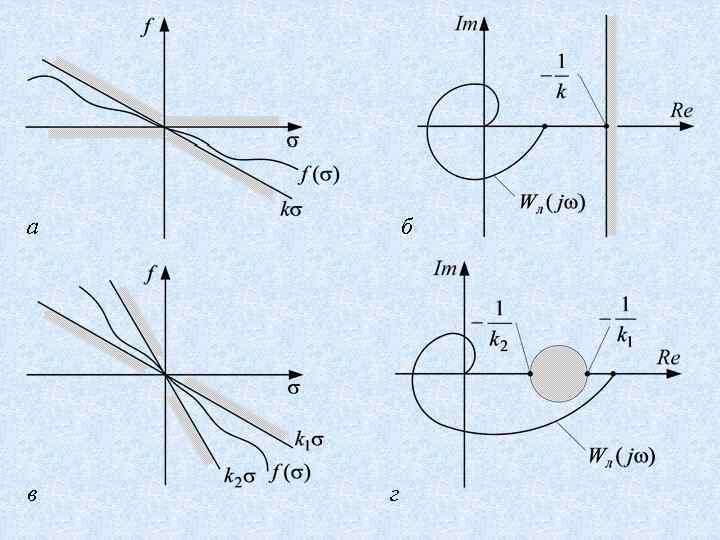
а в б г

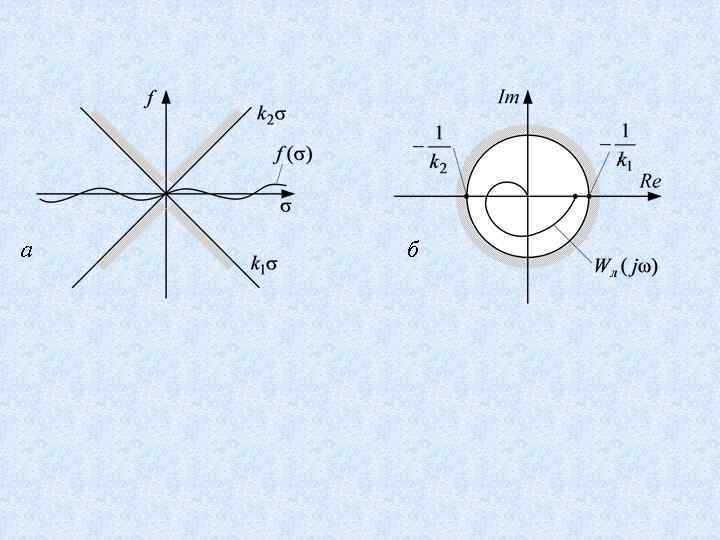
а б

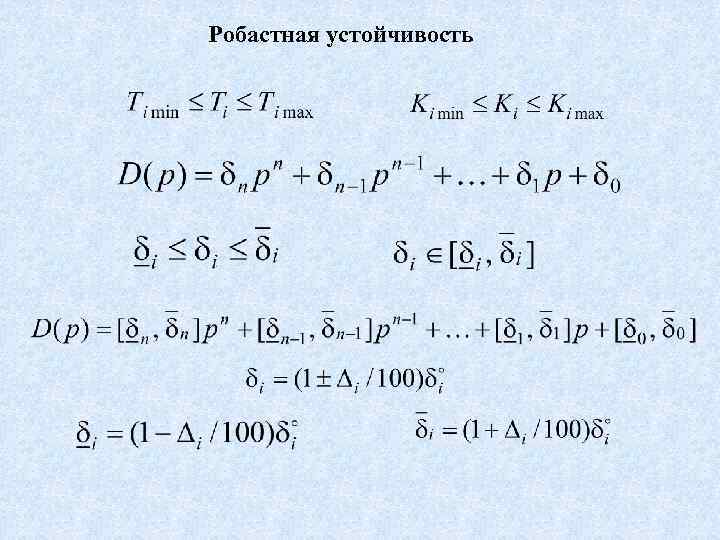
Робастная устойчивость

Определение. Динамическая система с характеристическим полиномом является робастно устойчивой, если она асимптотически устойчива в целом при любых значениях постоянных коэффициентов Критерий Харитонова

Пример Исследовать робастную устойчивость системы с характеристическим полиномом Решение Система робастно устойчива

Пример Оценить робастную устойчивость системы с характеристическим полиномом при 5% и 2% погрешности реализации его коэффициентов Решение

, , Система робастно неустойчива

185, 93>159, 94; 178, 63>166, 46; 193, 15>153, 64 Система робастно устойчива

ИССЛЕДОВАНИЕ НЕЛИНЕЙНЫХ СИСТЕМ МЕТОДАМИ ЛЯПУНОВА Понятие возмущенного и невозмущенного движения Решением системы является вектор

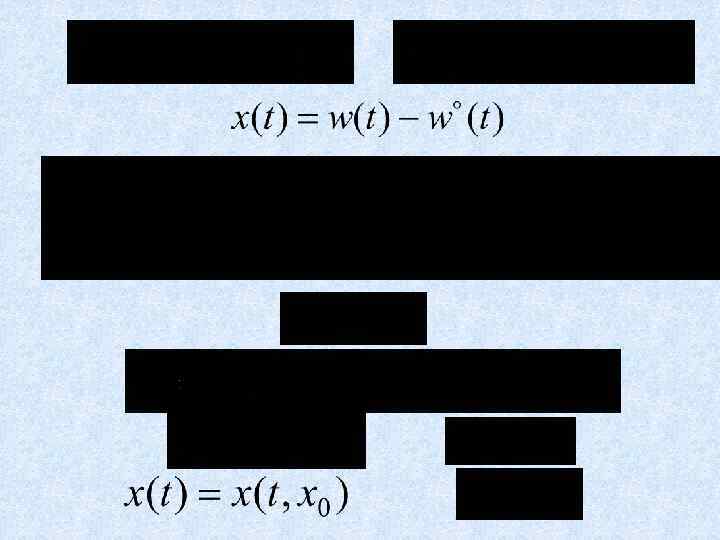
Метод первого приближения Уравнения первого приближения

Теоремы Ляпунова метода первого приближения. Обозначим через собственные числа матрицы , т. е. корни уравнения Теорема (об асимптотической устойчивости) Если вещественные части всех собственных чисел матрицы системы первого приближения строго меньше нуля, т. е. то невозмущенное движение нелинейной системы и положение равновесия системы асимптотически устойчивы.

Определение. Если при , где выполняются условия то положение равновесия устойчивым. – достаточно малое число, и называется асимптотически

Определение. Если областью притяжения положения равновесия некоторой системы является все фазовое пространство, то она называется асимптотически устойчивой в целом.

Теорема (о неустойчивости по первому приближению). Если среди собственных чисел матрицы системы первого приближения найдется хотя бы одно число с положительной вещественной частью, т. е. то невозмущенное движение нелинейной системы является неустойчивым Теорема (о невозможности исследования устойчивости по первому приближению). Если среди корней характеристического уравнения системы перво приближения имеется один или несколько с нулевыми вещественными частями, а остальные корни имеют отрицательную вещественную часть, то об устойчивости или неустойчивости невозмущенного движения нелинейной системы сказать ничего нельзя.

Пример Решение.

Система первого приближения Корни её характеристического уравнения

Метод функций Ляпунова

Определение. Функция называется положительно определенной, если при любом а при Определение. Функция если называется положительно полуопределённой, Отрицательно определенная функция

Определение. Функция если для любого числа сферы называется бесконечно большой, найдется такое, что вне имеет место неравенство Квадратичные формы. .

Критерий Сильвестра

Определение производной по времени вдоль траектории системы Пример Решение

Теорема (об асимптотической устойчивости). Если при всех существует положительно определенная функция такая, что её производная по времени вдоль траекторий системы является отрицательно определенной функцией, то положение равновесия этой системы асимптотически устойчиво в целом Теорема (о неустойчивости). Если при всех , существует положительно определенная функция такая, что ее производная по времени вдоль траекторий системы также является положительно определенной функцией, то положение равновесия такой системы неустойчиво.

Теорема (Барбашина-Красовского). Если при всех существует бесконечно большая положительно определенная функция такая, что ее производная по времени вдоль траекторий системы является отрицательно полуопределенной функцией, но обращается в нуль на множестве, не содержащем целых траекторий (кроме положения равновесия ) системы , то положение равновесия этой системы асимптотически устойчиво в целом.

Исследование систем методом функций Ляпунова Пример Исследовать устойчивость положения равновесия системы Решение.

Пример Исследовать методом функций Ляпунова устойчивость линейной системы, уравнение свободного движения которой в отклонениях имеет вид Решение здесь всегда Уравнение Ляпунова

Исследовать методом функций Ляпунова устойчивость нелинейной системы: где

Отредактировано до этого слайда

Пример Исследовать устойчивость положения равновесия системы, показанной на рис. , двумя (первым и вторым) методами Ляпунова, если , а y – отклонение выходной переменной. Решение.

Решение первым методом Ляпунова

Решение вторым методом Ляпунова: Построение функций Ляпунова Систем имеет одну нелинейность где Функция Ляпунова берется в виде: квадратичная форма + интеграл от нелинейности

Пример Исследовать устойчивость положения равновесия нелинейной системы

Решение. Далее слайд 124 Синтез систем методом функций Ляпунова Метод градиентного управления. Найти управление для системы:

Для определения функции а) б)

Пример Синтезировать градиентное управление для уменьшения бортовой качки корабля. Уравнение бортовой качки при отсутствии морского волнения имеет вид до

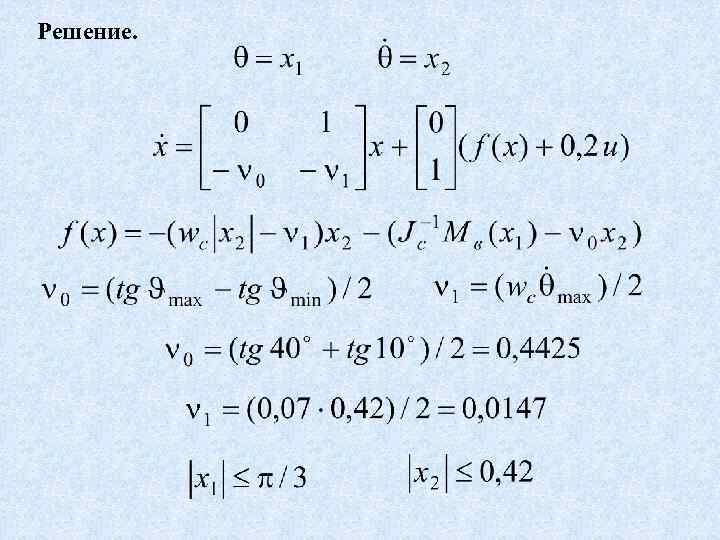
Решение.

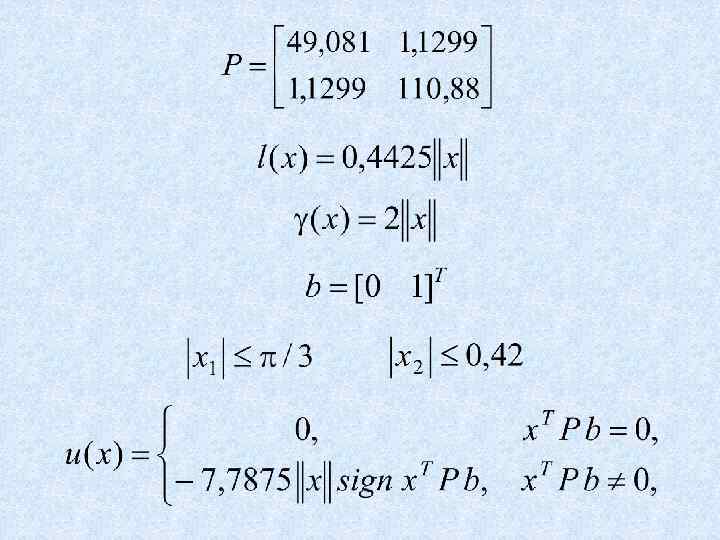
Синтез на основе квазилинейной модели

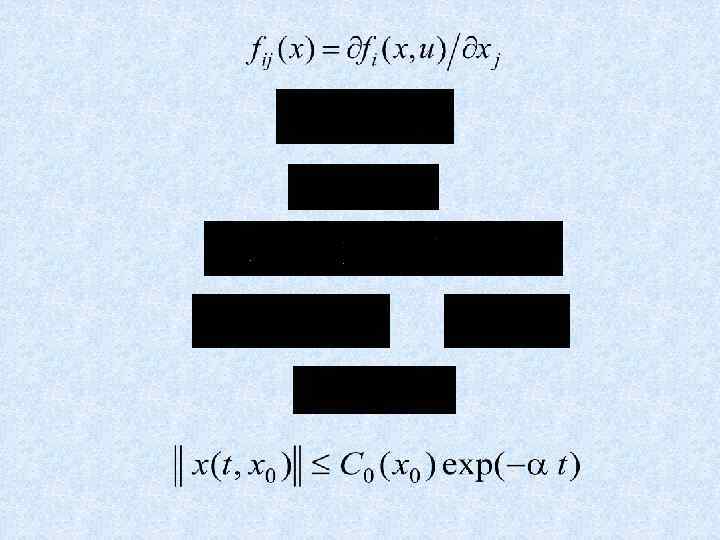
Теорема Если матрица является непрерывной, а коэффициенты её характеристического полинома – постоянными числами, и этот полином удовлетворяет критерию Гурвица, то существует некоторая область такая, что при всех и выполняется неравенство при

Пример Найти управление, стабилизирующее частоту синхронного генератора при постоянном напряжении возбуждения и отсутствии насыщения в магнитных цепях. Синхронный генератор и турбина описываются уравнениями в отклонениях Решение.

Продолжение синтеза на слайде 130

Построение функций Ляпунова (продолжение, начало на слайде 110) Метод деления переменных Барбашина

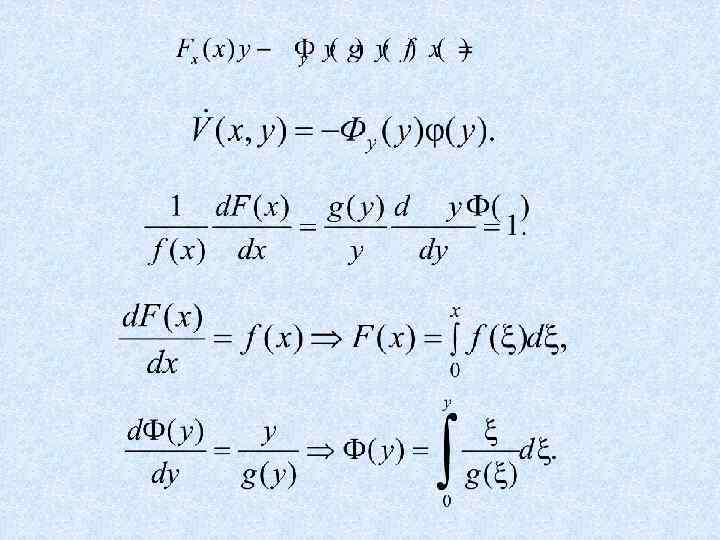
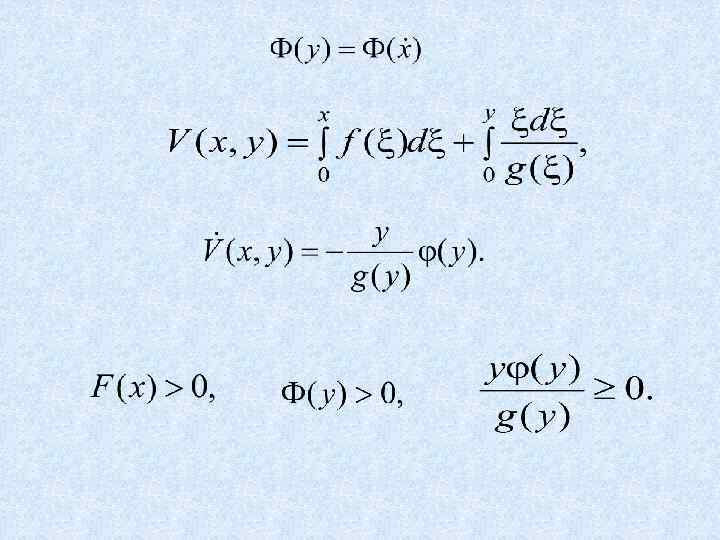
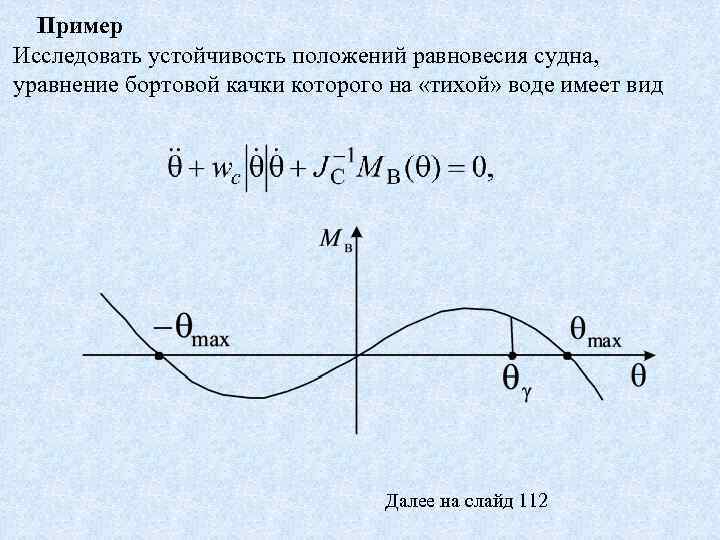
Пример Исследовать устойчивость положений равновесия судна, уравнение бортовой качки которого на «тихой» воде имеет вид Далее на слайд 112

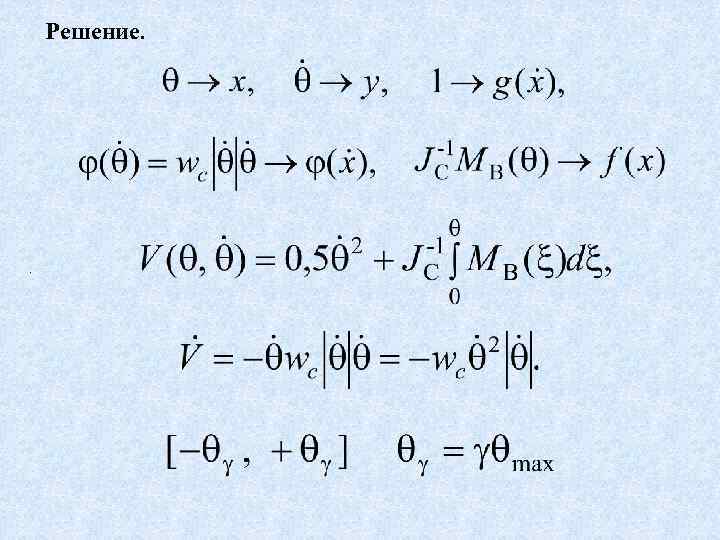
Решение. .

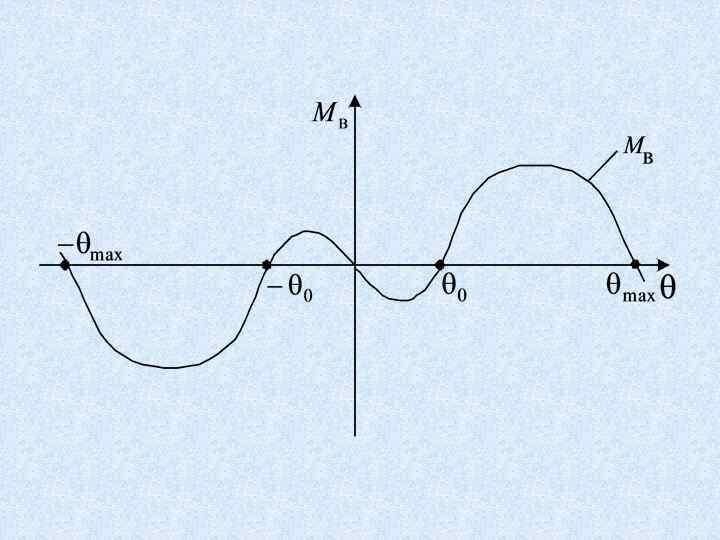
Синтез нелинейных систем на основе управляемой формы Жордана

Определение. Если нелинейности системы уравнений , , удовлетворяют условиям , то эта система уравнений называется управляемой формой Жордана. (для )

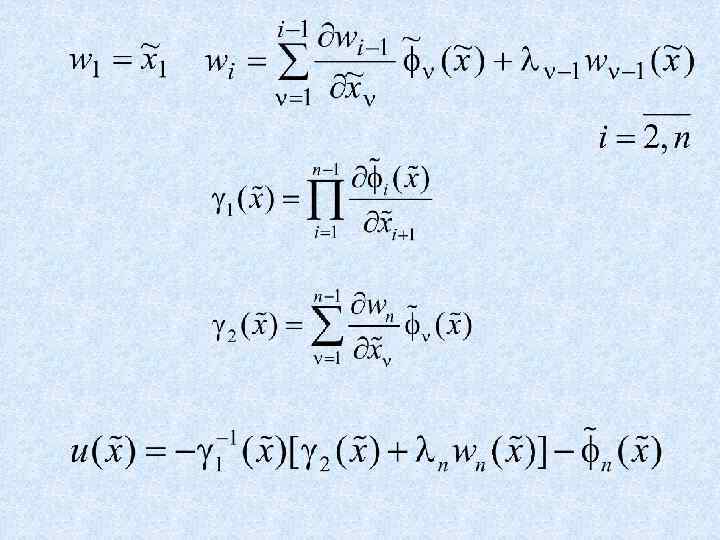
Пример. Найти управление, стабилизирующее частоту синхронного генератора при постоянном напряжении возбуждения и отсутствии насыщения в магнитных цепях. Синхронный генератор и турбина описываются дифференциальными уравнениями в отклонениях Проверяем условие управляемости: Система является управляемой формой Жордана. Решение задачи синтеза.

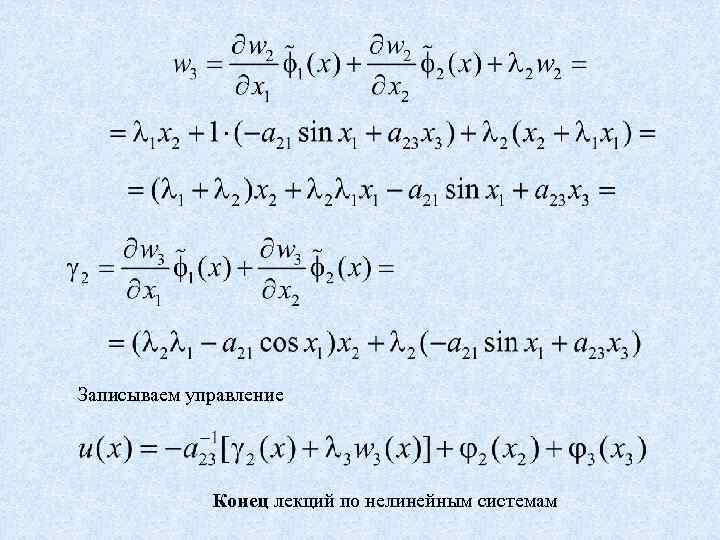
Записываем управление Конец лекций по нелинейным системам