Нелинейные резистивные элементы (НРЭ)






















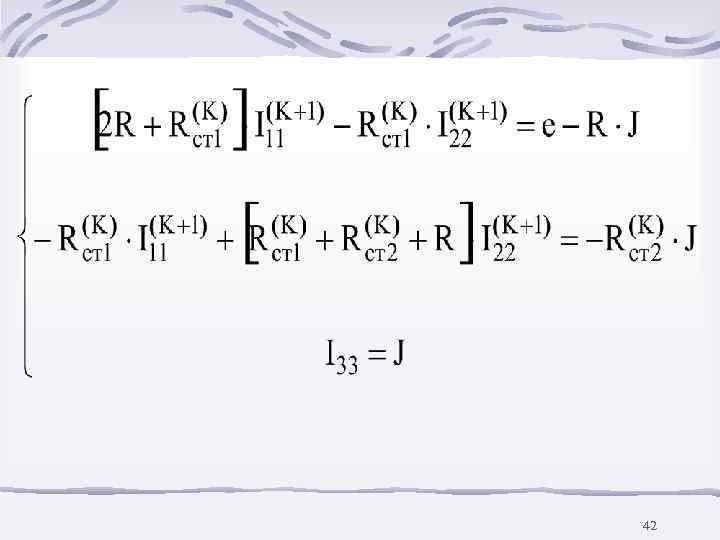




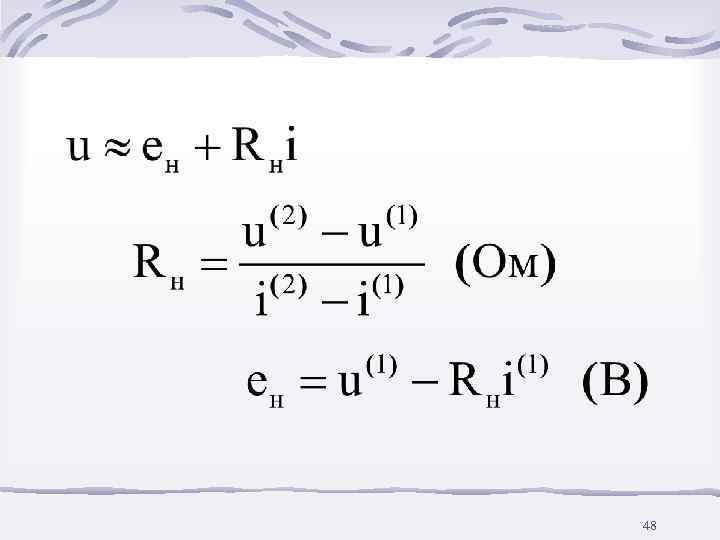




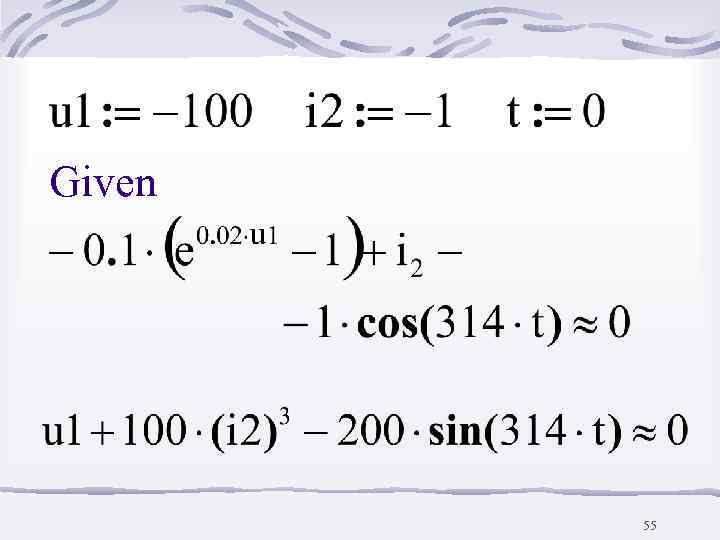



Лек-17 НРЭ п_ тока.ppt
- Количество слайдов: 59
 Нелинейные резистивные элементы (НРЭ) 1
Нелинейные резистивные элементы (НРЭ) 1
 НРЭ имеют нелинейную ВАХ i(u) и необратимо преобразуют электрическую энергию в тепло 2
НРЭ имеют нелинейную ВАХ i(u) и необратимо преобразуют электрическую энергию в тепло 2
 К нелинейным резистивным элементам относятся, например: 3
К нелинейным резистивным элементам относятся, например: 3
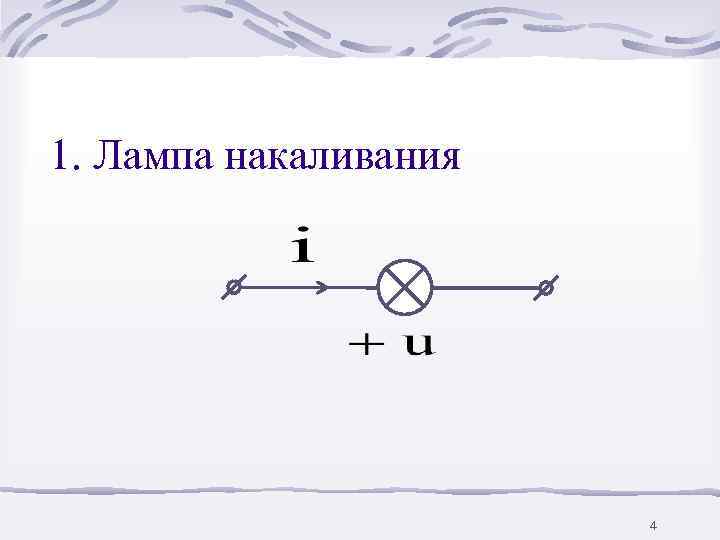
 1. Лампа накаливания 4
1. Лампа накаливания 4
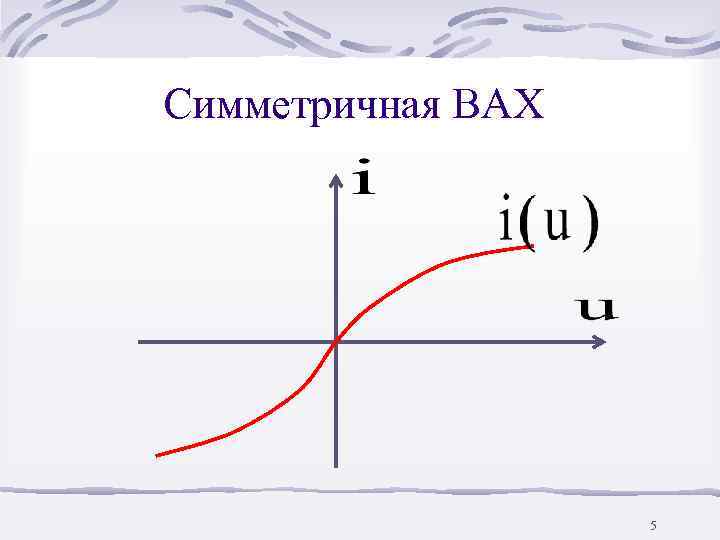
 Симметричная ВАХ 5
Симметричная ВАХ 5
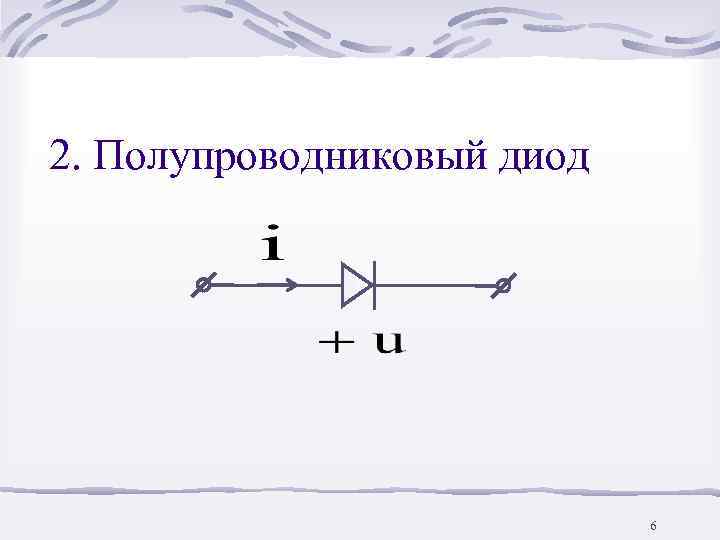
 2. Полупроводниковый диод 6
2. Полупроводниковый диод 6
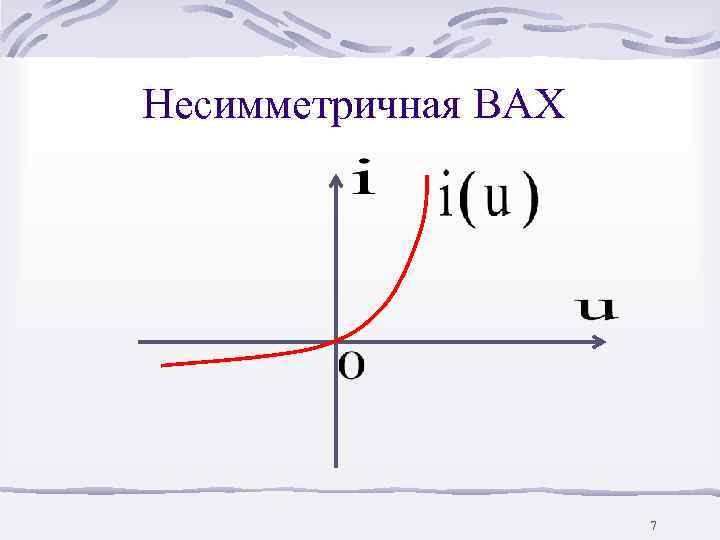
 Несимметричная ВАХ 7
Несимметричная ВАХ 7
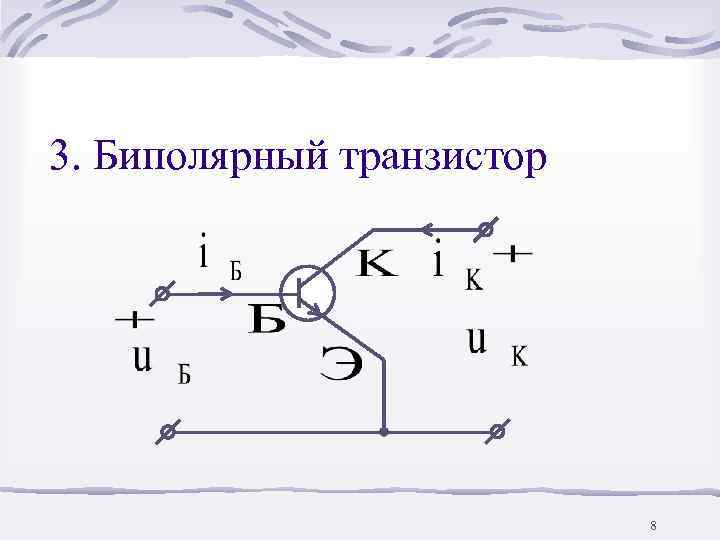
 3. Биполярный транзистор 8
3. Биполярный транзистор 8
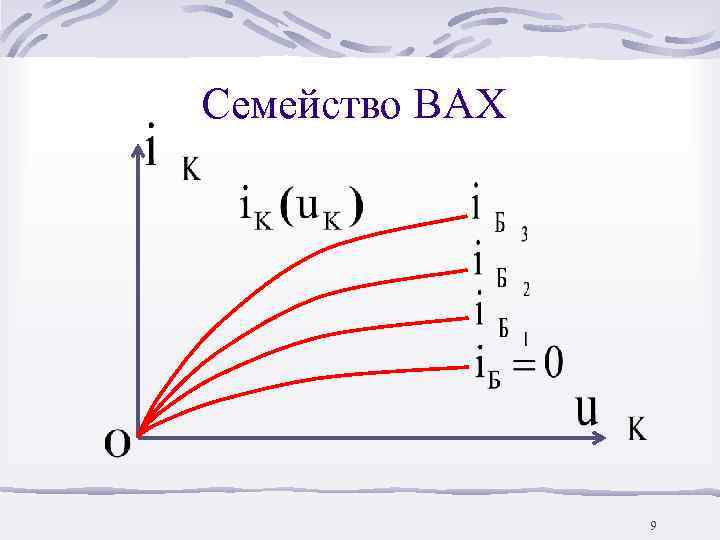
 Семейство ВАХ 9
Семейство ВАХ 9
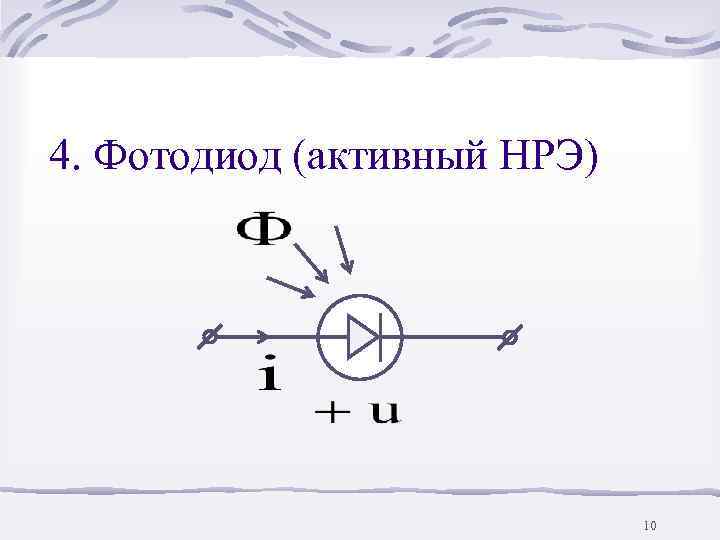
 4. Фотодиод (активный НРЭ) 10
4. Фотодиод (активный НРЭ) 10
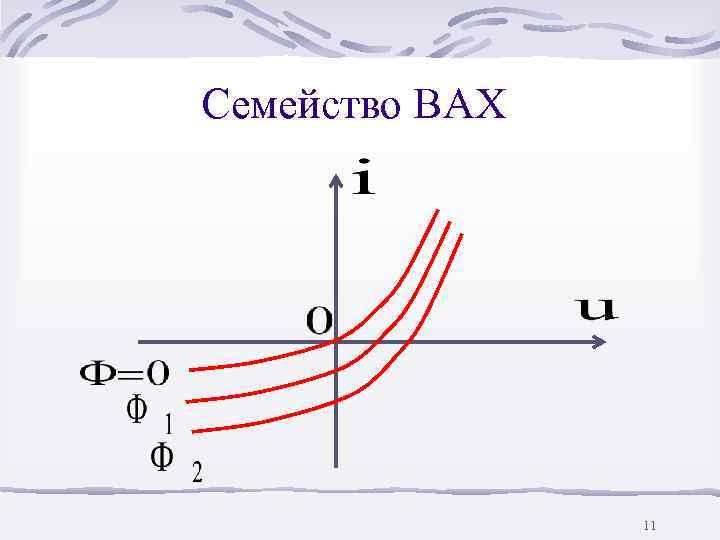
 Семейство ВАХ 11
Семейство ВАХ 11
 Лампа накаливания – инерционный пассивный НРЭ с симметричной ВАХ i(u) 12
Лампа накаливания – инерционный пассивный НРЭ с симметричной ВАХ i(u) 12
 Полупроводниковый диод – безынерционный пассивный НРЭ с несимметричной ВАХ i(u) 13
Полупроводниковый диод – безынерционный пассивный НРЭ с несимметричной ВАХ i(u) 13
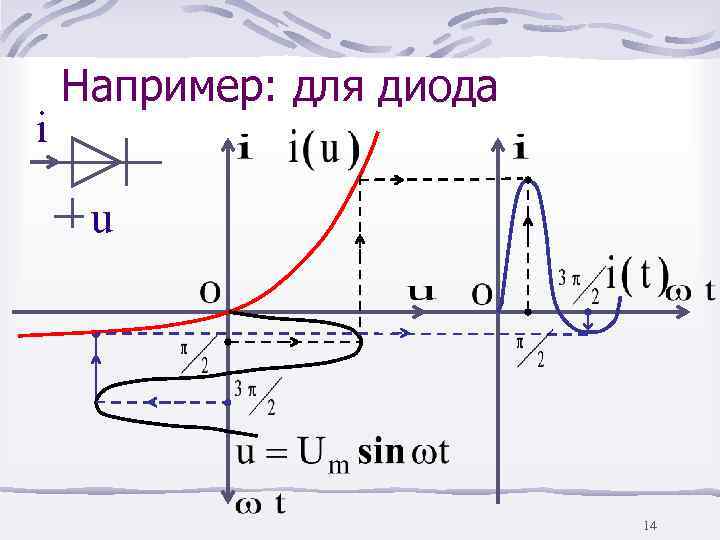
 Например: для диода i u 14
Например: для диода i u 14
 Безынерционные элементы являются источником высших гармоник 15
Безынерционные элементы являются источником высших гармоник 15
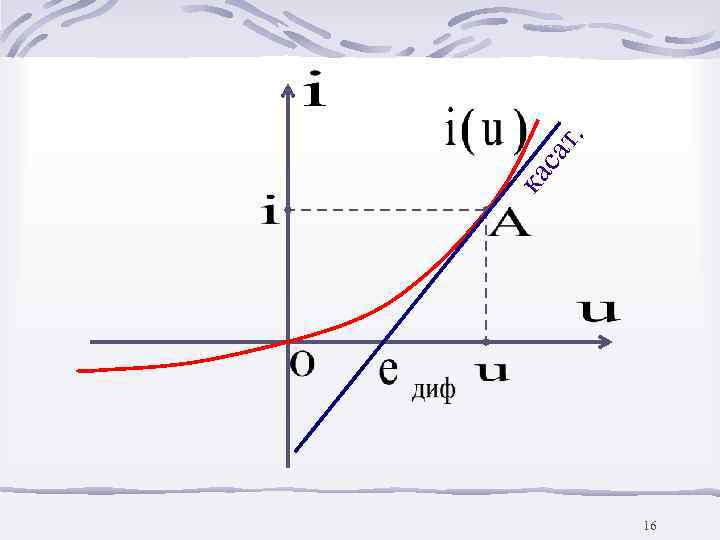
 ка са т. 16
ка са т. 16
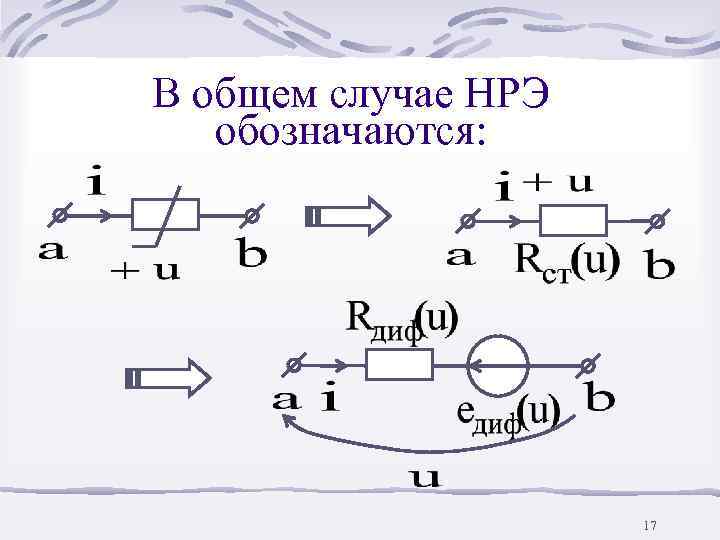
 В общем случае НРЭ обозначаются: 17
В общем случае НРЭ обозначаются: 17
 Статическое сопротивление 18
Статическое сопротивление 18
 Дифференциальное сопротивление 19
Дифференциальное сопротивление 19
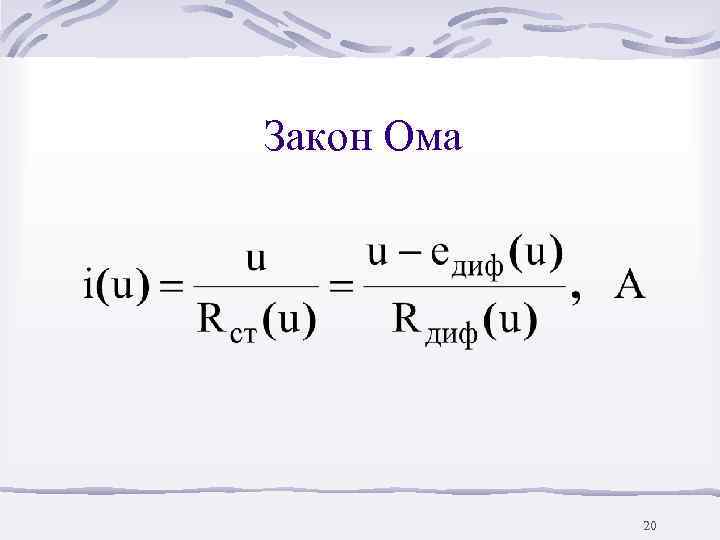
 Закон Ома 20
Закон Ома 20
 Закон Джоуля-Ленца 21
Закон Джоуля-Ленца 21
 Расчет нелинейных резистивных цепей 22
Расчет нелинейных резистивных цепей 22
 Ведется графоаналитическими методами с использованием статических или динамических ВАХ НРЭ 23
Ведется графоаналитическими методами с использованием статических или динамических ВАХ НРЭ 23
 При этом расчет нелинейных резистивных цепей при переменных напряжениях и токах осуществляется для мгновенных значений для каждого момента времени по отдельности 24
При этом расчет нелинейных резистивных цепей при переменных напряжениях и токах осуществляется для мгновенных значений для каждого момента времени по отдельности 24
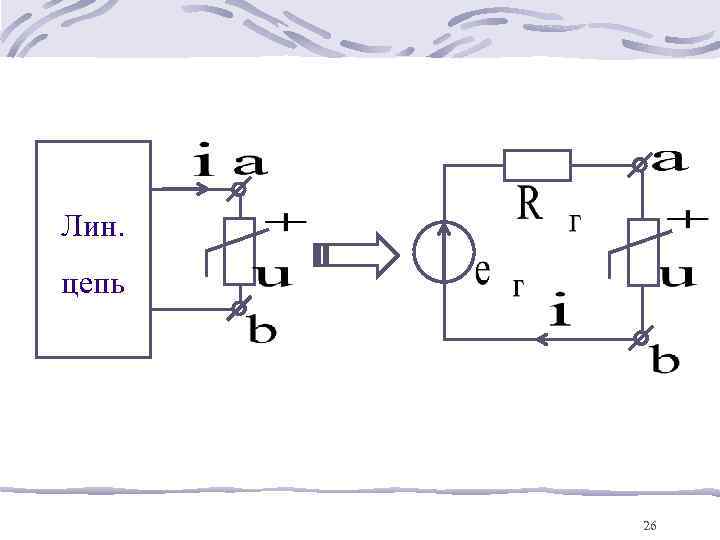
 1. Метод эквивалентного генератора – применяется для цепей с одним НРЭ 25
1. Метод эквивалентного генератора – применяется для цепей с одним НРЭ 25
 Лин. цепь 26
Лин. цепь 26
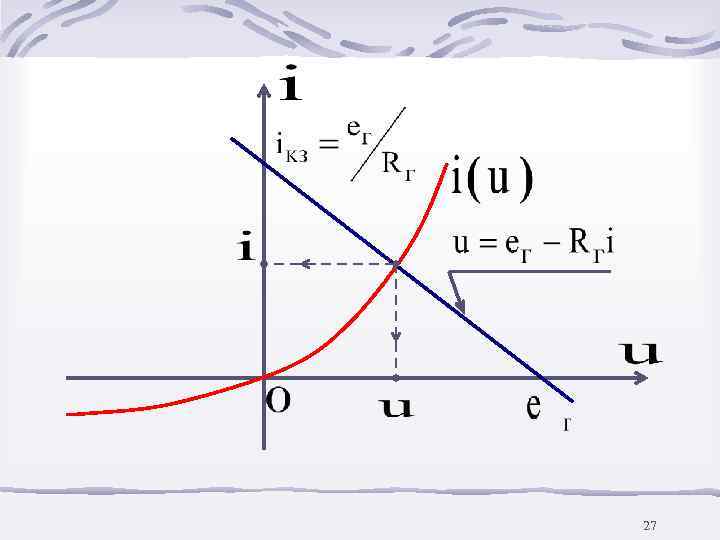
 27
27
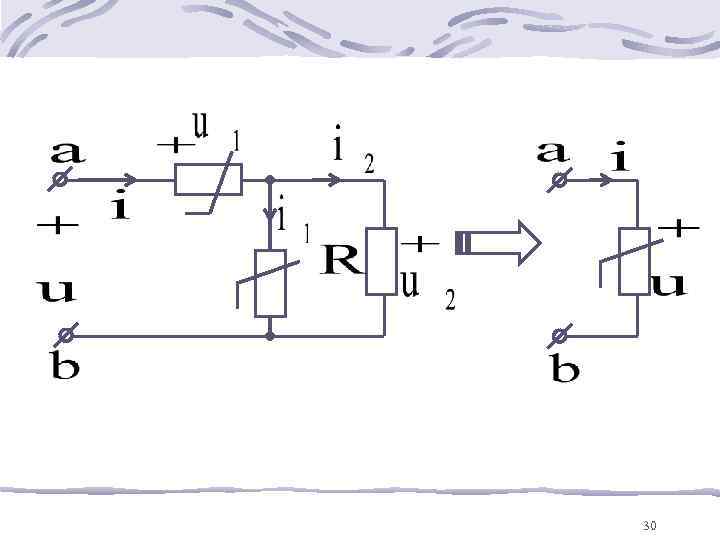
 2. Сложение ВАХ – применяется для упрощения схем 28
2. Сложение ВАХ – применяется для упрощения схем 28
 При этом на основании законов Кирхгофа ВАХ i(u) последовательно соединенных НРЭ складываются вдоль оси u, а ВАХ параллельно соединенных НРЭ складываются вдоль оси i 29
При этом на основании законов Кирхгофа ВАХ i(u) последовательно соединенных НРЭ складываются вдоль оси u, а ВАХ параллельно соединенных НРЭ складываются вдоль оси i 29
 30
30
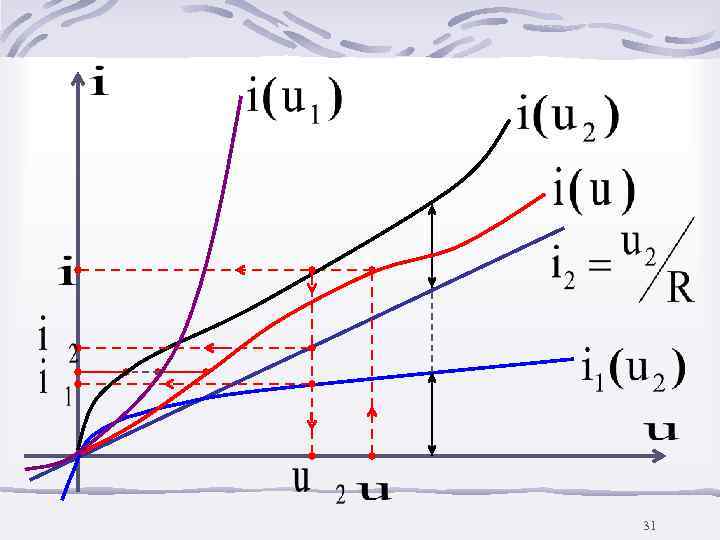
 31
31
 3. Метод двух узлов – применяется для схем с двумя узлами 32
3. Метод двух узлов – применяется для схем с двумя узлами 32
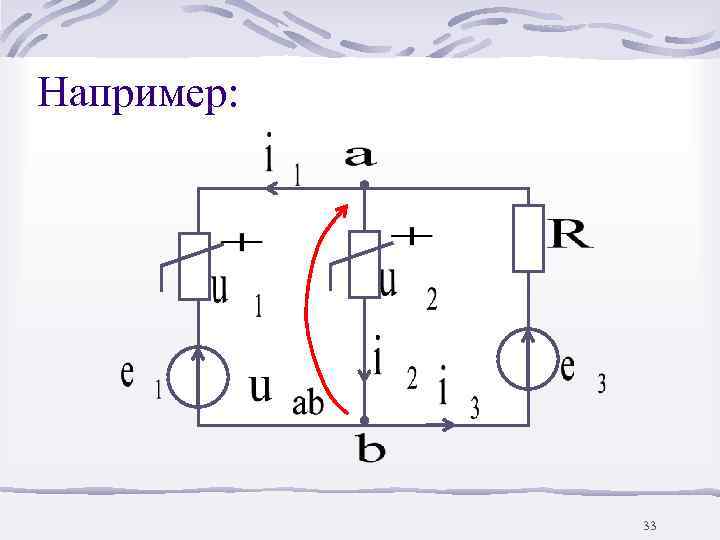
 Например: 33
Например: 33
 Уравнения по законам Кирхгофа: 34
Уравнения по законам Кирхгофа: 34
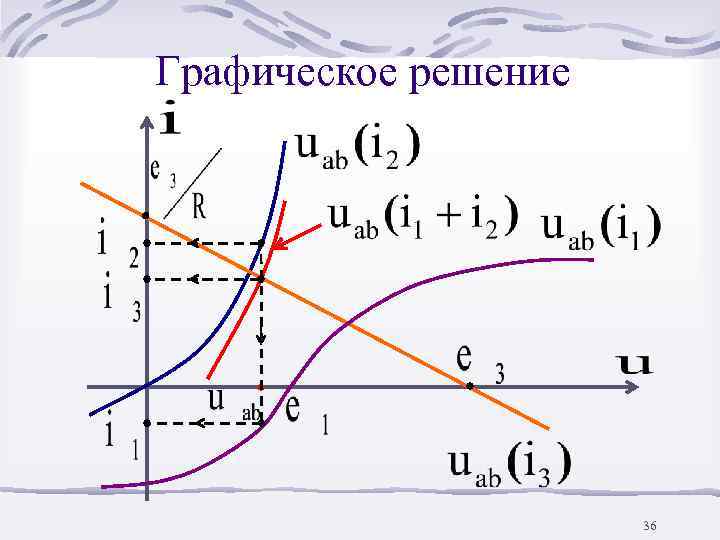
 Так как i 3=i 1+i 2 , то uab(i 1) и uab(i 2) складываем вдоль оси i, причем точка пересечения полученной ВАХ uab(i 1+i 2) с uab(i 3) даст решение 35
Так как i 3=i 1+i 2 , то uab(i 1) и uab(i 2) складываем вдоль оси i, причем точка пересечения полученной ВАХ uab(i 1+i 2) с uab(i 3) даст решение 35
 Графическое решение 36
Графическое решение 36
 4. Метод итераций – применяется для расчета схем с использованием вычислительной техники 37
4. Метод итераций – применяется для расчета схем с использованием вычислительной техники 37
 При этом НРЭ обозначаются в виде неизвестных статических сопротивлений Rст , причем для лучшей сходимости итерационное выражение составляется для тока в НРЭ если его ВАХ загибается к оси i, иначе составляется для u 38
При этом НРЭ обозначаются в виде неизвестных статических сопротивлений Rст , причем для лучшей сходимости итерационное выражение составляется для тока в НРЭ если его ВАХ загибается к оси i, иначе составляется для u 38
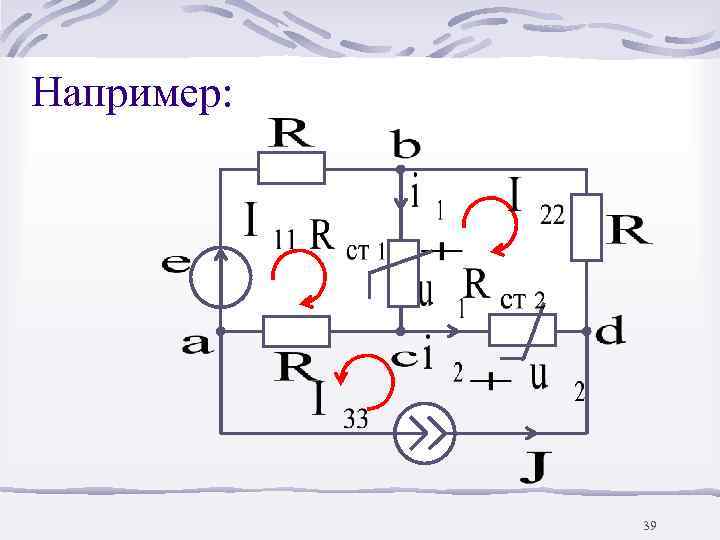
 Например: 39
Например: 39
 40
40
 Для расчета статических сопротивлений и используем метод контурных токов 41
Для расчета статических сопротивлений и используем метод контурных токов 41
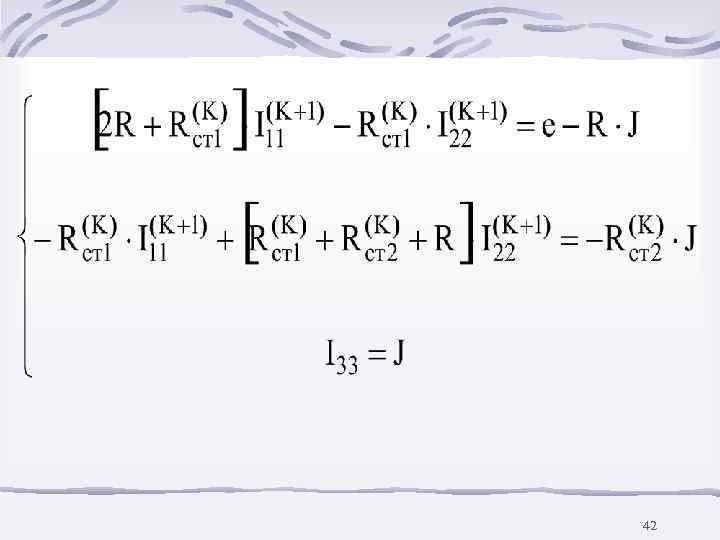 42
42
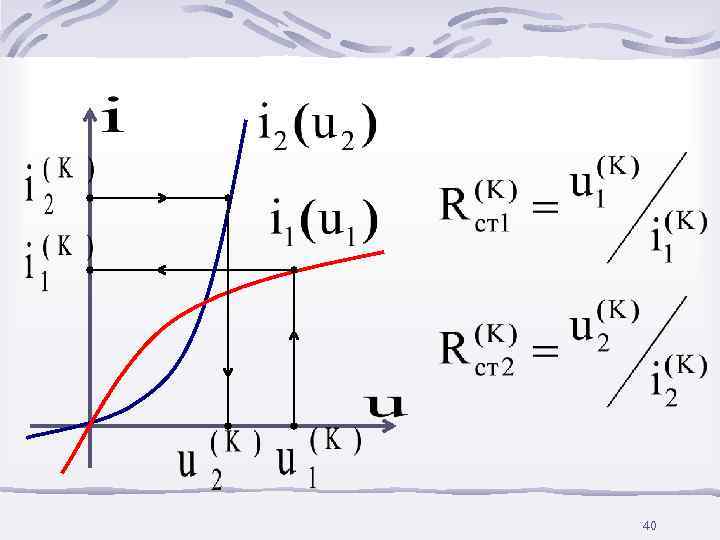
 Итерационные выражения 43
Итерационные выражения 43
 Задаемся произвольными значениями u 1 (0) и i (0), по ВАХ 2 находим i 1 (0) и u (0), рассчитываем 2 RCT 1(0) и RCT 2(0), по итерационным выражениям определяем u 1(1) и i 2(1), по ВАХ находим i 1(1) и u 2(1), и т. д. 44
Задаемся произвольными значениями u 1 (0) и i (0), по ВАХ 2 находим i 1 (0) и u (0), рассчитываем 2 RCT 1(0) и RCT 2(0), по итерационным выражениям определяем u 1(1) и i 2(1), по ВАХ находим i 1(1) и u 2(1), и т. д. 44
 Расчет ведется до повторения результатов 45
Расчет ведется до повторения результатов 45
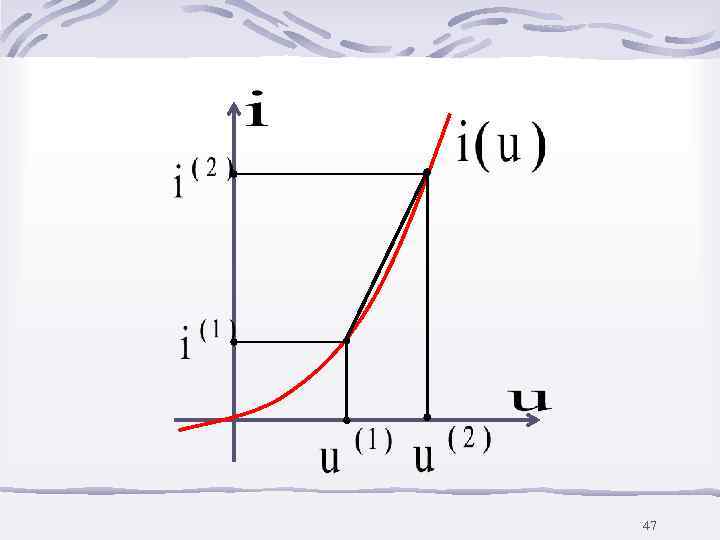
 5. Метод линеаризации ВАХ в области предполагаемого решения – применяется как приближенный метод 46
5. Метод линеаризации ВАХ в области предполагаемого решения – применяется как приближенный метод 46
 47
47
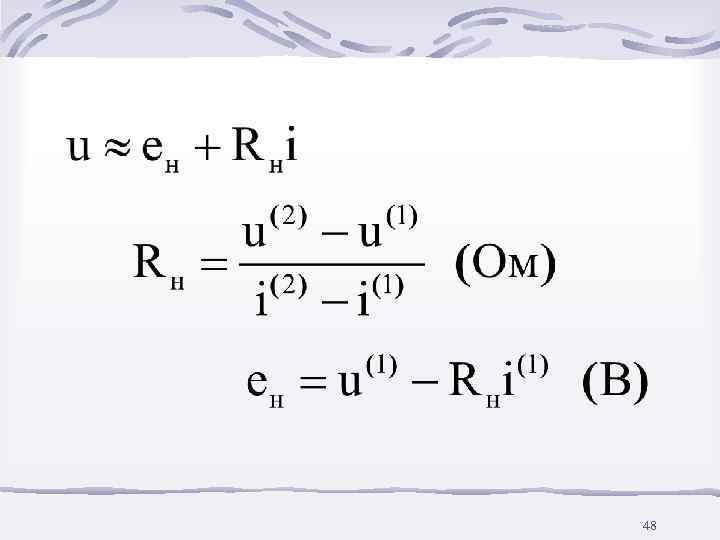 48
48
 49
49
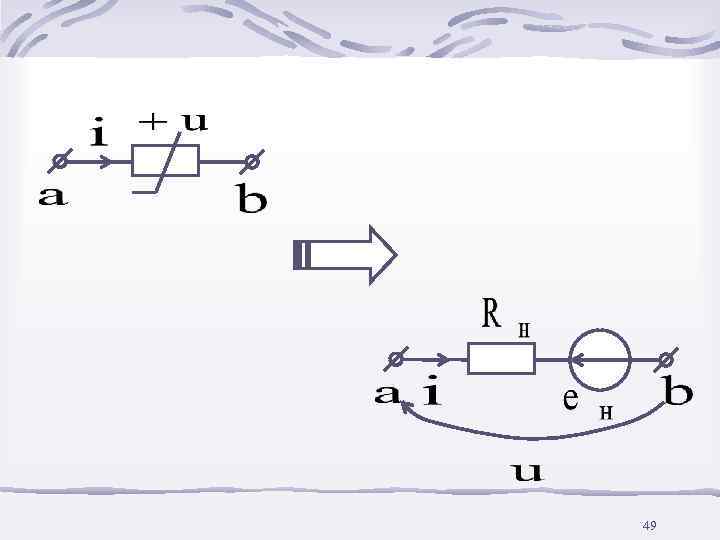
 После замены нелинейных элементов линейными резисторами Rн и ЭДС eн расчет ведется любым методом. Если найденные токи i лежат в выбранных интервалах i(1)
После замены нелинейных элементов линейными резисторами Rн и ЭДС eн расчет ведется любым методом. Если найденные токи i лежат в выбранных интервалах i(1)
 6. Применение MATHCAD на ЭВМ для расчета переменных напряжений и токов 51
6. Применение MATHCAD на ЭВМ для расчета переменных напряжений и токов 51
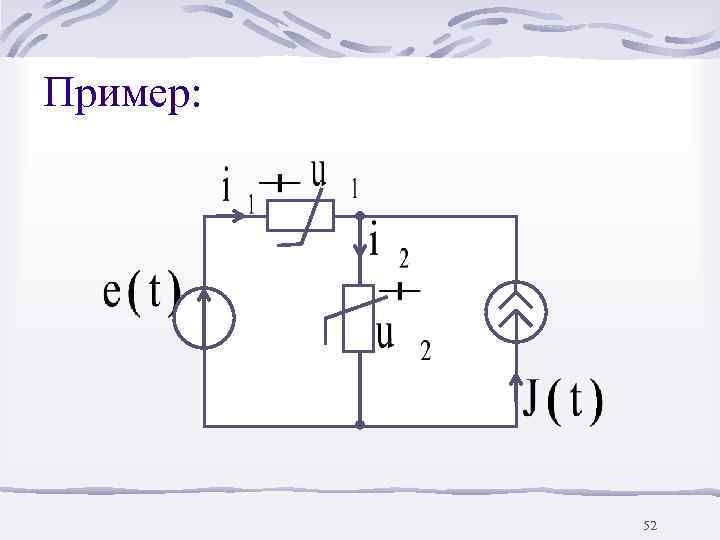
 Пример: 52
Пример: 52
 Дано: 53
Дано: 53
 По законам Кирхгофа 54
По законам Кирхгофа 54
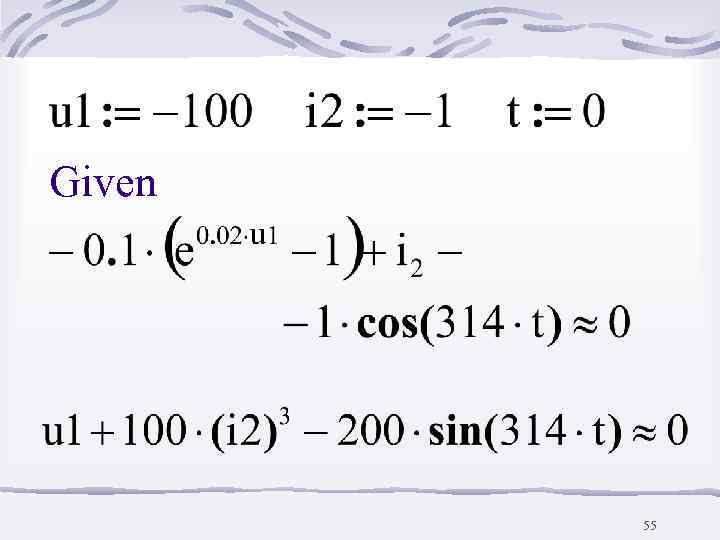 Given 55
Given 55
 Find 56
Find 56
 57
57
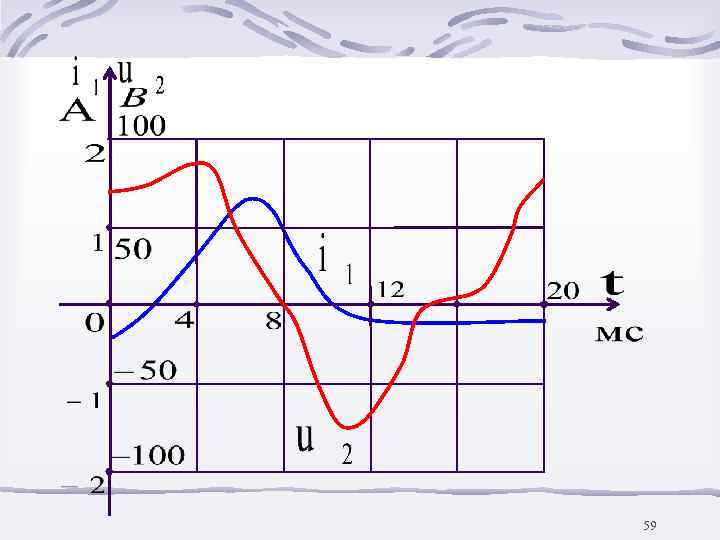
 Изменяем и повторяем расчет. Затем строим графики, например, i 1(t) и u 2(t) 58
Изменяем и повторяем расчет. Затем строим графики, например, i 1(t) и u 2(t) 58
 59
59

