Нелинейные АСУ Курс лекций по дисциплине Теория автоматического

Нелинейные АСУ Курс лекций по дисциплине «Теория автоматического управления» Кафедра «Автоматизированные электромеханические системы» Лектор: доцент Шамардина Вера Николаевна

Литература, рекомендуемая при изучении курса: • Власов К. П. Теория автоматического управления. Учебное пособие. : Х. : Изд-во Гуманитарный центр, 2007. - 526 с. • Попович М. Г. , Ковальчук О. В. Теорiя автоматичного керування: Пiдручник. - К. : Либiдь, 1997. -544 с. • Иващенко Н. Н. Автоматическое регулирование. Теория и элементы систем. Учебник для вузов. Изд. 4 -е перераб. и доп. - М. : Машиностроение, 1978. - 736 с. • Юревич Е. И. Теория автоматического управления. 2 -е изд. Л. : Энергия, 1975. - 416 с. • Попов Е. П. Теория нелинейных систем автоматического регулирования и управления. М. : Наука, 1988. - 256 с. • Современные системы управления/ Р. Дорф, Р. Бишоп. Пер. с англ. Б. И. Копылова. - М. : Лаборатория Базовых Знаний, 2002. - 832 с. • Теорія автоматического керування: Навчальний посібник/ Артюшин Л. М. и др. -Львів: Вид-во УАД, 2004. -272 с.

Нелинейные АСУ. Основные определения. Нелинейная АСУ – это система, содержащая хотя бы одно нелинейное звено, описываемое нелинейным уравнением. Все реальные системы нелинейные, Однако, если рассматривать малые отклонения от точки заданного режима работы, реальную АСУ путем линеаризации можно представить линейной моделью и применять для её исследования известные методы теории линейных систем. Звенья, нелинейностью которых нельзя пренебречь (нельзя линеаризовать) называют существенно нелинейными. Они играют определяющую роль в поведении системы. В этом случае необходимо применять методы теории нелинейных АСУ.

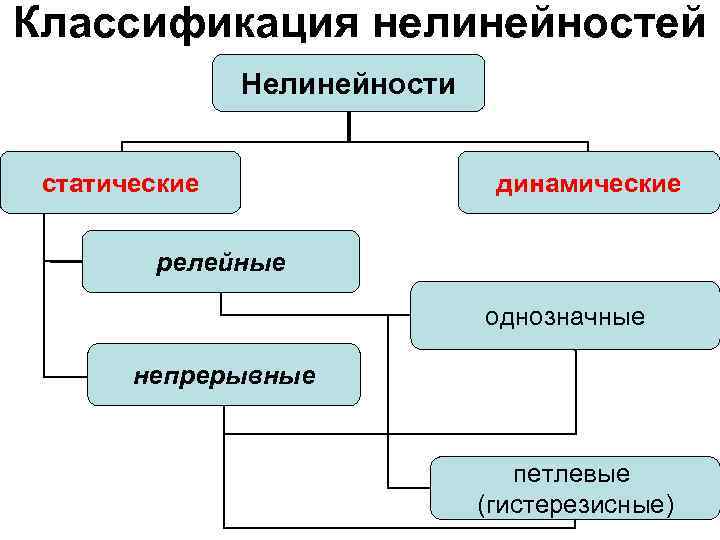Классификация нелинейностей Нелинейности статические динамические релейные однозначные непрерывные петлевые (гистерезисные)

• Будем рассматривать АСУ с одним нелинейным статическим блоком. Этот класс АСУ наиболее простой, и для него разработаны эффективные методы исследования некоторых ключевых вопросов динамики. • Общей теории нелинейных АСУ не существует, т. к. они отличаются исключительным многообразием и нет общего решения нелинейных дифференциальных уравнений (только частные решения).

Нелинейности в АСУ могут быть : естественно присущие (трение, люфт, гистерезис, насыщение, зона нечувствительности), они часто оказывают вредное влияние на работу АСУ и его необходимо устранять или ограничивать. специально вводимые нелинейности придают системе желаемые свойства (релейные элементы, нелинейные корректирующие устройства и т. п. )

Статические нелинейности Некоторые нелинейные статические характеристики u(x) = N(x) = F[X(∞)] встречаются чаще других, и могут быть с достаточной степенью точности аппроксимированы кусочно-линейными функциями. Эти характеристики называются типовыми. Ниже приводится таблица графиков типовых статических характеристик.

Однозначные нелинейности. Статическая характеристика Математическое описание Рис. 1 Н. э. – ограничение (насыщение) Если |x|a, то u=c·sign(x) НЭ 1 Рис. 2 Н. э. – переменный коэф. усиления (2 значения ) Если |x|a, то u= k 2·x-a·(k 2 k 1)·sign(x)

рис. 3 н. э. – переменный коэф. усиления (3 значения) НЭ 3 Рис. 4 Н. э. –нечувствительность НЭ 4 Если |x|≤ b 1, то u= k 1·x если b 1<|x|< b 2, то u= k 2·x + B 2·sign(x), если |x|≥ b 2, то u=k 3·x + B 3·sign(x), где B 2=b 1·(k 1 -k 2) B 3=b 1·( k 1 -k 2) + (k 2 -k 3)·b 2 если |x|≤a, то u=0 если |x|>a, то u=k·x - k·a·sign(x)

Рис. 5 Н. э. – нечувствительность и переменный коэффициент усиления НЭ 5 Рис. 6 Н. э. – нечувствительность и ограничение Если |x|≤a, то u=0 если a<|x|b, то u=c ·sign(x) Если |x|≤a, то u=0 если a<|x|b, то u=k 2·x + B 2·sign(x) B 1=-k 1·a

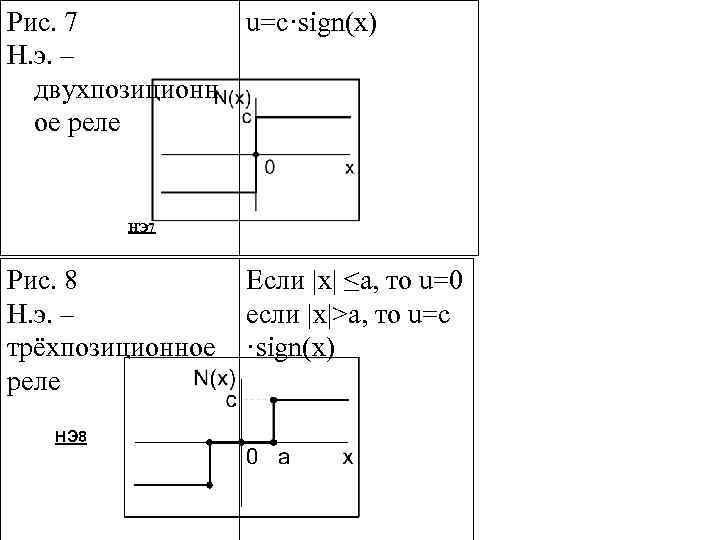Рис. 7 u=c·sign(x) Н. э. – двухпозиционн ое реле НЭ 7 Рис. 8 Н. э. – трёхпозиционное реле НЭ 8 Если |x| ≤a, то u=0 если |x|>a, то u=c ·sign(x)

Реле с обычным гистерезисом Рис. 9. Н. э. – двухпозиционное реле с гистерезисом НЭ 9 Рис. 10. Н. э. – трёхпозиционное реле с гистерезисом НЭ 10 если | xn |>a, то un = sign(xn) если | xn |b, то un = с·sign(xn) при |x|=а или |x|=b, выходной сигнал скачком изменяет своё значение, как показано на рисунке 10

Динамические нелинейные звенья описываются нелинейными дифференциальными или интегральными уравнениями. Примеры: • пара трения (сухое трение). В простейшем случае: Fтр c Fтр = Csigndx/dt при dx/dt ≠ 0 0 dx dt -C ≤ Fтр ≤ C при dx/dt = 0

• Звено с изменяющейся постоянной времени Постоянная времени зависит от координат (или их производных), а не от времени. [T(x)p+1]y(p) = k x(p). Пример. Электромагнитная постоянная времени обмотки возбуждения генератора постоянного тока: Tв = Lв/Rв. Индуктивность обмотки возбуждения нелинейно зависит от тока возбуждения (нелинейная кривая намагничивания машины) Lв = f (iв), поэтому Tв = F (iв). Ф Lв iв iв

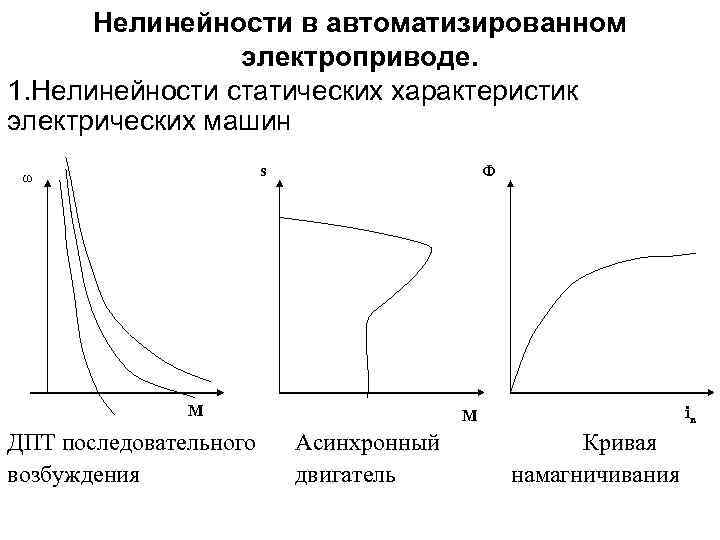Нелинейности в автоматизированном электроприводе. 1. Нелинейности статических характеристик электрических машин Ф s ω М ДПТ последовательного возбуждения iв M Асинхронный двигатель Кривая намагничивания

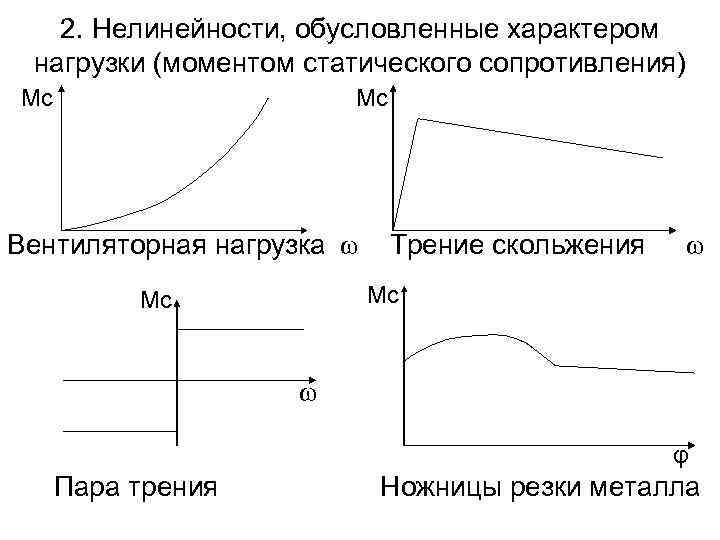2. Нелинейности, обусловленные характером нагрузки (моментом статического сопротивления) Mс Mс Вентиляторная нагрузка ω Трение скольжения ω Mс Mс ω φ Пара трения Ножницы резки металла

3. Нелинейности, обусловленные конструкцией и свойствами передаточных устройств электропривода (шлицевые, шпоночные, зубчатые и т. д. ) Mс Mс (φ1 - φ2) Зубчатая передача (φ1 - φ2) Муфты резиновые

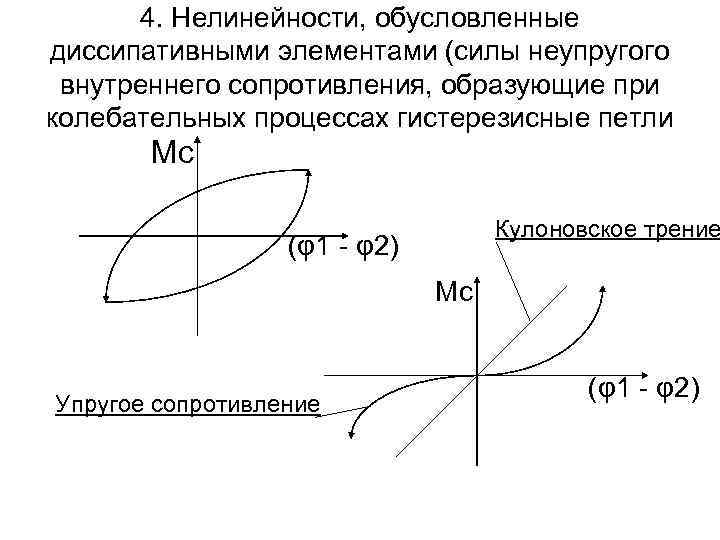4. Нелинейности, обусловленные диссипативными элементами (силы неупругого внутреннего сопротивления, образующие при колебательных процессах гистерезисные петли Mс Кулоновское трение (φ1 - φ2) Mс Упругое сопротивление (φ1 - φ2)

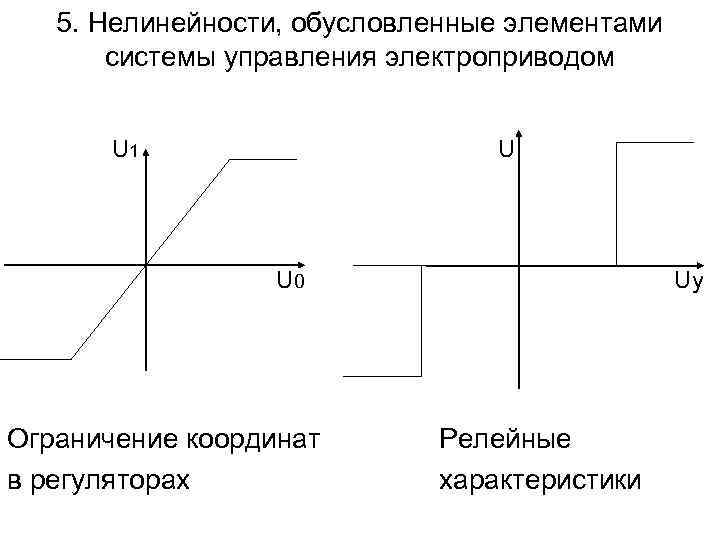5. Нелинейности, обусловленные элементами системы управления электроприводом U 1 U U 0 Ограничение координат в регуляторах Uу Релейные характеристики

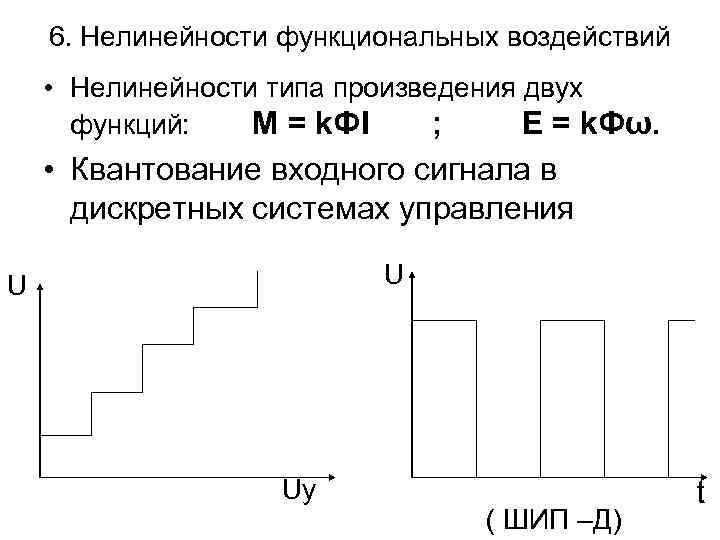6. Нелинейности функциональных воздействий • Нелинейности типа произведения двух функций: М = k. ФI ; E = k. Фω. • Квантование входного сигнала в дискретных системах управления U U Uу ( ШИП –Д) t

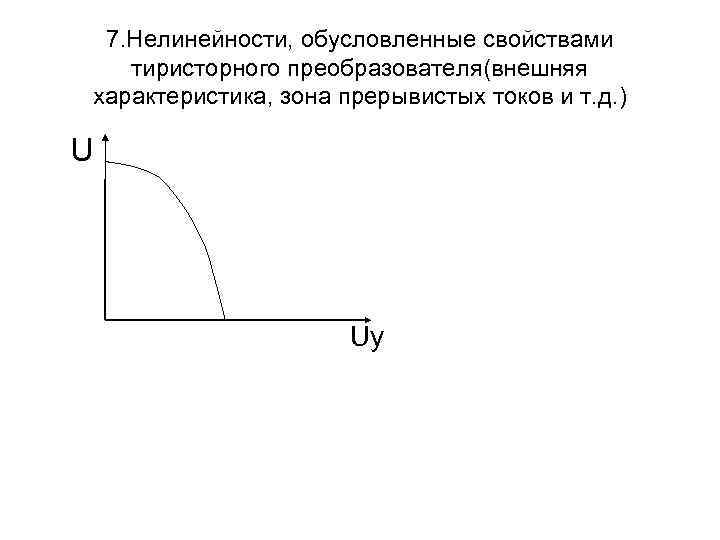7. Нелинейности, обусловленные свойствами тиристорного преобразователя(внешняя характеристика, зона прерывистых токов и т. д. ) U Uу

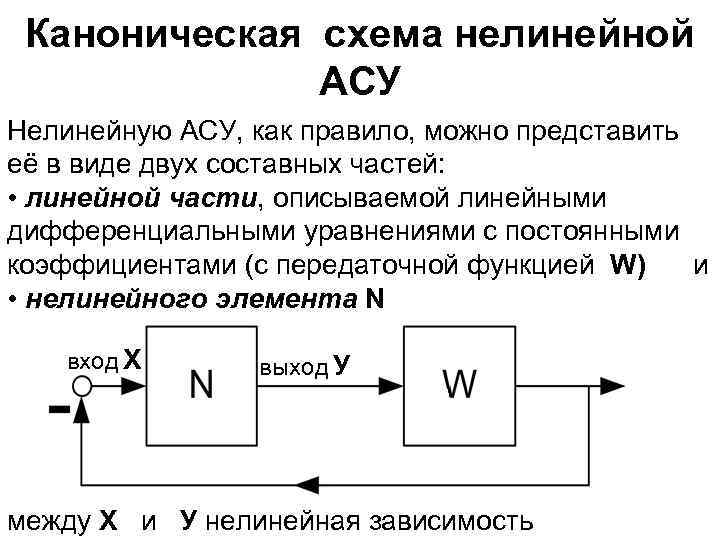Каноническая схема нелинейной АСУ Нелинейную АСУ, как правило, можно представить её в виде двух составных частей: • линейной части, описываемой линейными дифференциальными уравнениями с постоянными коэффициентами (с передаточной функцией W) и • нелинейного элемента N вход Х выход У между Х и У нелинейная зависимость

Структурные преобразования нелинейных АСУ Позволяют упростить сложную многоконтурную АСУ и привести её к эквивалентной одноконтурной. Особенности преобразований обусловлены тем, что: 1. для нелинейных АСУ неприменим принцип суперпозиции; 2. независимо от выполняемых преобразований амплитуда на входе нелинейного элемента (НЭ) должна оставаться неизменной, поэтому нельзя перемещать звенья через НЭ. Преобразование линейных звеньев, находящихся до и после НЭ, осуществляется по известным правилам, а НЭ должен сохранять свое исходное расположение в АСУ.

Получение эквивалентной нелинейности • При последовательном соединении НЭ: НЭ 1 x НЭ 2 Y 1 i Xi = X 1 i Y 2 i Y Yi Y 2 i = Xni Y 1 i = X 2 i X 1 i НЭn X 2 i Yni =Yi Xni Для ряда значений Xi по статической характеристике НЭ 1 определим Y 1 i = X 2 i, далее по характеристике НЭ 2 найдем Y 2 i = Xni, а по характеристике НЭn Yni =Yi. Строим по точкам Y = f(x).

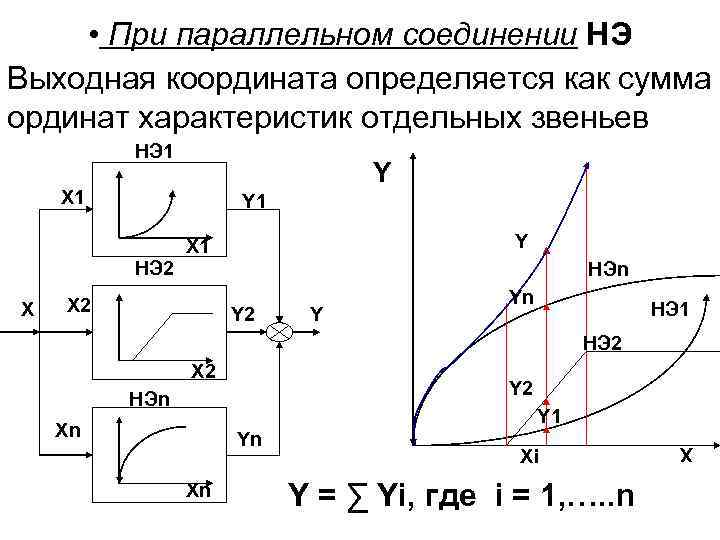• При параллельном соединении НЭ Выходная координата определяется как сумма ординат характеристик отдельных звеньев НЭ 1 Y X 1 Y 1 НЭ 2 НЭn X 2 Y Yn НЭ 1 НЭ 2 X 2 Y 2 НЭn Y 1 Xn Yn Xn Xi Y = ∑ Yi, где i = 1, …. . n X X Y X 1

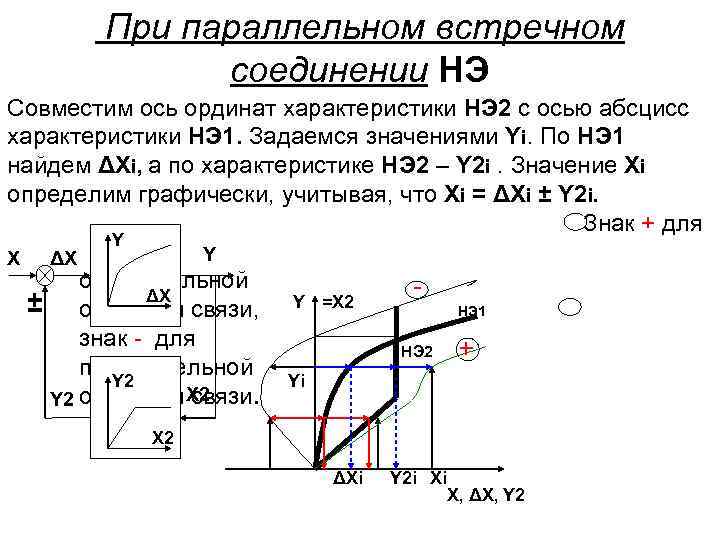При параллельном встречном соединении НЭ Совместим ось ординат характеристики НЭ 2 с осью абсцисс характеристики НЭ 1. Задаемся значениями Yi. По НЭ 1 найдем ΔXi, а по характеристике НЭ 2 – Y 2 i. Значение Xi определим графически, учитывая, что Xi = ΔXi ± Y 2 i. Знак + для X ΔX Y Y отрицательной ΔX ± обратной связи, знак - для положительной Y 2 связи. Y 2 обратной X 2 Y =X 2 НЭ 1 НЭ 2 + Yi X 2 ΔXi Y 2 i Xi X, ΔX, Y 2

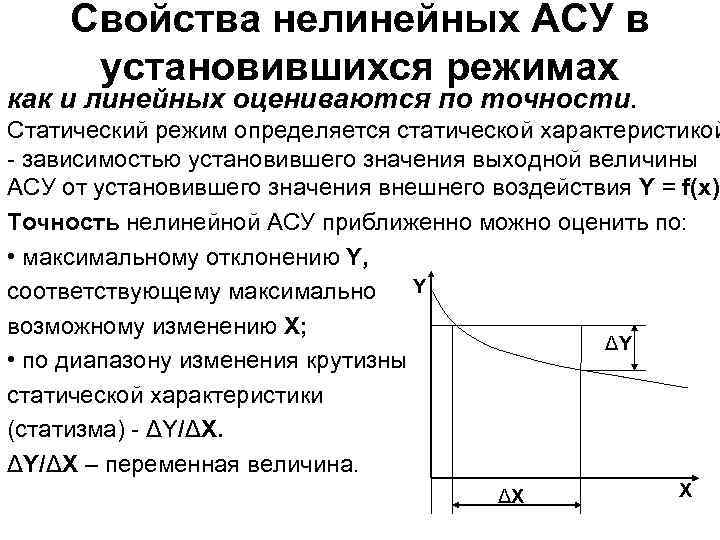Свойства нелинейных АСУ в установившихся режимах как и линейных оцениваются по точности. Статический режим определяется статической характеристикой - зависимостью установившего значения выходной величины АСУ от установившего значения внешнего воздействия Y = f(x). Точность нелинейной АСУ приближенно можно оценить по: • максимальному отклонению Y, Y соответствующему максимально возможному изменению Х; ΔY • по диапазону изменения крутизны статической характеристики (статизма) - ΔY/ΔX – переменная величина. ΔХ Х

Особенности нелинейных систем обусловлены неподчинением принципу суперпозиции: 1. При подаче гармонического сигнала на вход НЭ на выходе колебания могут отличаться от входного гармонического сигнала как по форме, так и по частоте. yнэ (x) =| x | При подаче на вход x(t) = Asin ωt выходные колебания не гармонические, они совершенно другой формы и период вдвое меньший, чем период входных колебаний. В линейных же системах при подаче на вход гармонического сигнала на выходе получаем также гармонический сигнал, но другой амплитуды и сдвинутый по фазе.

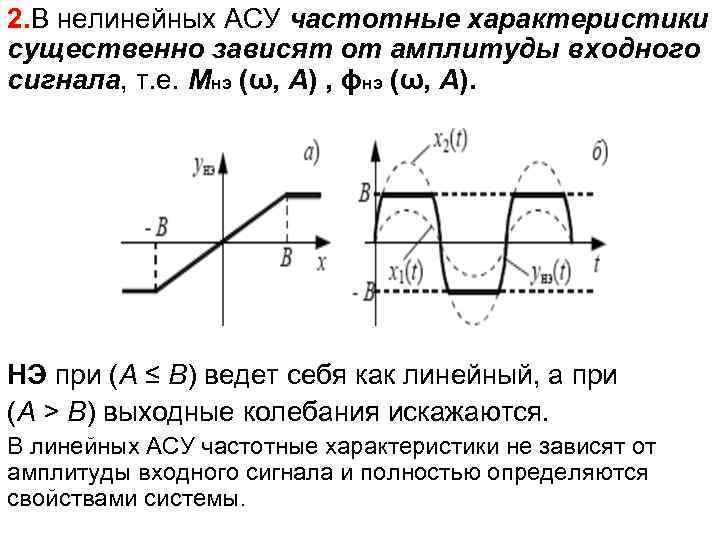2. В нелинейных АСУ частотные характеристики существенно зависят от амплитуды входного сигнала, т. е. Mнэ (ω, A) , ϕнэ (ω, A). НЭ при (A ≤ B) ведет себя как линейный, а при (A > B) выходные колебания искажаются. В линейных АСУ частотные характеристики не зависят от амплитуды входного сигнала и полностью определяются свойствами системы.

3. В нелинейных АСУ условия устойчивости зависят от величины внешнего воздействия: АСУ, устойчивая при одних значениях воздействий, неустойчива при других его значениях. Можно говорить лишь об устойчивости конкретного состояния равновесия – устойчиво оно или нет. Нельзя говорить однозначно, устойчива АСУ или нет. Для нелинейных АСУ применяют понятие "устойчивость в малом", "устойчивость в большом", "устойчивость в целом". АСУ устойчива в малом, если она устойчива только при малых начальных отклонениях. АСУ устойчива в большом, если она устойчива при больших начальных отклонениях. АСУ устойчива в целом, если она устойчива при любых начальных отклонениях.

4. В нелинейных АСУ могут существовать собственные особые движения, названные автоколебаниями (АК). Это устойчивые собственные колебания, обусловленные наличием НЭ. Режим (АК) принципиально отличается от колебаний линейной АСУ на границе устойчивости, когда малейшие изменения ее параметров приводят к изменению колебательного процесса, и он становится либо сходящимся, либо расходящимся. (АК) являются устойчивым режимом, если малые изменения параметров системы не выводят ее из этого режима. (АК) могут быть и не устойчивым режимом, если малые изменения параметров системы выведут ее из этого режима. Амплитуда АК не зависит от начальных условий и уровня внешних воздействий. Часто (АК) в нелинейных АСУ нежелательны, иногда и недопустимы. Однако, в некоторых нелинейных АСУ (АК) являются основным рабочим режимом.

Наличие АК не означает, что нелинейная АСУ не работоспособна! • АК могут иметь очень малую амплитуду не могут оказывать заметного влияния на работу АСУ, • В АСУ принципиально возможны АК , но для их возникновения к АСУ должны быть приложены практически невозможные воздействия. Перечисленные особенности нелинейных АСУ требуют при их исследовании обязательно оговаривать начальные условия и величину внешнего воздействия.

Методы исследования нелинейных АСУ 1. Методы линейной теории (метод замены нелинейных характеристик аналитическими зависимостями, метод кусочно-линейной аппроксимации, метод гармонической линеаризации и др. ). 2. Численные методы интегрирования нелинейных дифференциальных уравнений. 3. Графо-аналитические и графические. 4. Методы математического моделирования

Две задачи имеют особое значение для анализа динамики нелинейных АСУ: • Определить условия, при которых нелинейная АСУ подобна линейной. Она имеет единственное положение равновесия и приходит к нему при любых начальных отклонениях ее координат. Такой класс систем называется абсолютно устойчивыми системами. • Найти условия, при которых в АСУ имеют место автоколебания (АК). Выяснить, какова область их притяжения. В общем случае это очень трудная задача. Однако, для многих практически важных случаев разработаны методы ее точного или приближенного решения.

Динамика нелинейных АСУ. При изучении курса рассмотрим два подхода к исследованию динамики: • Первый – метод фазового пространства (метод пространства состояний). Он позволяет провести полное исследование системы, но очень сложен даже при использовании современных ПК. • Второй - применение частотных методов. Эти методы отличаются простотой и наглядностью, но позволяют провести лишь частичный анализ.

Метод фазового пространства Фазовое пространство - это пространство, где прямоугольными координатами точки являются величины, определяющие мгновенное состояние системы, называемые фазовыми координатами. В КАЧЕСТВЕ ФАЗОВЫХ КООРДИНАТ ВЫБИРАЮТ ВЫХОДНУЮ КООРДИНАТУ СИСТЕМЫ И ЕЕ ПРОИЗВОДНЫЕ. Метод применим как для линейных, так и для нелинейных систем. (Метод переменных состояний).

Понятие "фазовое пространство" связано с процедурой перехода от нелинейных дифференциальных уравнений (ДУ) высокого порядка n к системе из n нелинейных (ДУ) 1 -го порядка. F(Y (n) , Y, U (m), U, K) = 0, где Y (n) – n-я производная, F – нелинейная функция, Y (n) = ϕ (Y (n− 1), K) – нелинейное дифференциальное уравнение k-го порядка относительно Y. Фазовое пространство нелинейной АСУ – это многомерное векторное пространство, точки x которого имеют координаты: Фазовое пространство иллюстрирует решение данного (ДУ). Эффективность этого понятия наиболее видна в двухмерном фазовом пространстве.

В автоматике принято, что: "Всякий переходный процесс может быть в первом приближении представлен в виде системы не сложнее 3 -го порядка; система 2 -го порядка описывает колебательность с затуханием и добавление 3 -го порядка (в случае необходимости) усложняет процесс затухания". Т. е. , часто бывает достаточно 2 -го порядка. В случае, когда фазовое пространство двухмерно, а этот случай часто встречается на практике, использование этого пространства становится очень наглядным.

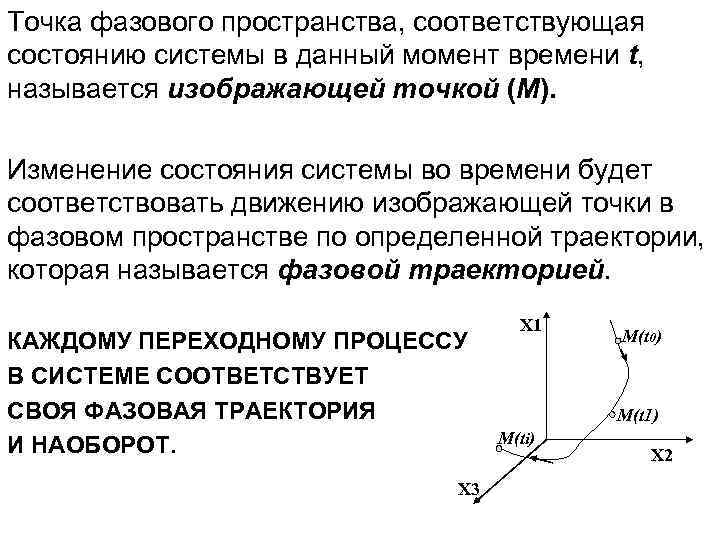Точка фазового пространства, соответствующая состоянию системы в данный момент времени t, называется изображающей точкой (М). Изменение состояния системы во времени будет соответствовать движению изображающей точки в фазовом пространстве по определенной траектории, которая называется фазовой траекторией. КАЖДОМУ ПЕРЕХОДНОМУ ПРОЦЕССУ В СИСТЕМЕ СООТВЕТСТВУЕТ СВОЯ ФАЗОВАЯ ТРАЕКТОРИЯ И НАОБОРОТ. Х 3 Х 1 М(t 0) М(t 1) М(ti) Х 2

НАПРАВЛЕНИЕ ДВИЖЕНИЯ НА ТРАЕКТОРИИ ОТМЕЧАЮТ СТРЕЛКАМИ. ДВИЖЕНИЕ ИЗОБРАЖАЮЩЕЙ ТОЧКИ ПО ФАЗОВОЙ ТРАЕКТОРИИ ПРОИСХОДИТ ПО ЧАСОВОЙ СТРЕЛКЕ ВОКРУГ НАЧАЛА КООРДИНАТ. Для систем 2 -го порядка фазовое пространство – это плоскость. По оси абсцисс: х- выходная координата, а по оси ординат: y=dx/dt– скорость изменения выходной координаты –x(t). В верхних квадрантах у >0, и изображающая точка движется всегда слева направо в направлении увеличения х(t). В нижних квадрантах у<0, и изображающая точка движется всегда справа налево y=dx/dt в направлении уменьшения х(t). На оси абсцисс y=dx/dt =0(точка экстремума), поэтому фазовые траектории пересекают ось абсцисс под прямым углом, т. к. x(t) достигает х(t) своего максимума.

Методы построения фазовых портретов СОВОКУПНОСТЬ ФАЗОВЫХ ТРАЕКТОРИЙ, СООТВЕТСТВУЮЩИХ ВСЕМ ВОЗМОЖНЫМ В ДАННОЙ СИСТЕМЕ НАЧАЛЬНЫМ УСЛОВИЯМ, НАЗЫВАЕТСЯ ФАЗОВЫМ ПОРТРЕТОМ СИСТЕМЫ. Пусть АСУ описывается ДУ: Понизим порядок ДУ: Разделим первое уравнение на второе. Тем самым исключим из уравнений t. В результате получим нелинейное ДУ 1 -го порядка: РЕШЕНИЕ ЭТОГО УРАВНЕНИЯ ДАЕТ СЕМЕЙСТВО ИНТЕГРАЛЬНЫХ КРИВЫХ НА ФАЗОВОЙ ПЛОСКОСТИ, ПО КОТОРЫМ СТРОЯТСЯ ФАЗОВЫЕ ТРАЕКТОРИИ СИСТЕМЫ.

Решение ДУ фазовой траектории можно получить следующими методами: • ИНТЕГРИРОВАНИЕМ УРАВНЕНИЙ ФАЗОВЫХ ТРАЕКТОРИЙ В линейных АСУ интегрирование ДУ фазовых траекторий не представляет трудностей. Для нелинейных АСУ эта задача существенно усложняется. Аналитическое решение часто получить не удается, поэтому для построения фазовых портретов нелинейных АСУ применяют численное интегрирование уравнения.

МЕТОД ИЗОКЛИН имеет невысокую точность и используется для качественной оценки хода фазовых траекторий. Изоклина -кривая, представляющая геометрическое место точек фазового пространства, в которых касательные ко всем интегральным кривым наклонены под одним и тем же углом к оси абсцисс. Этапы построения фазового портрета методом изоклин : 1. Построение изоклин; 2. Нанесение направления касательных к фазовым траекториям; 3. Определение характера искомого фазового портрета.

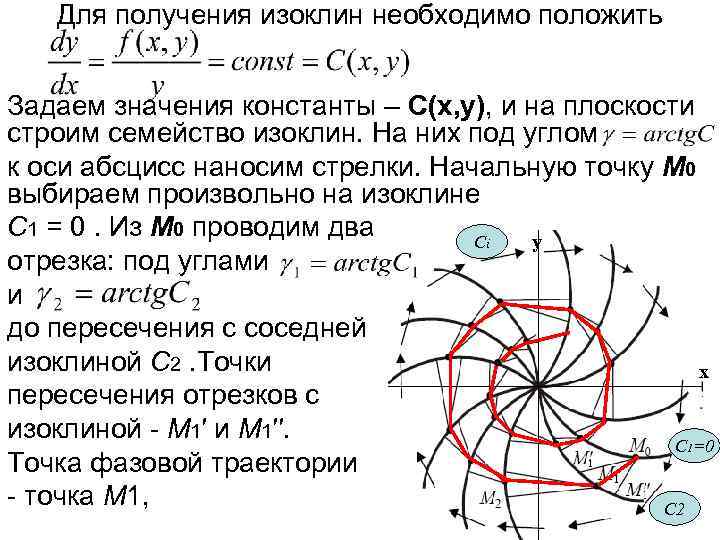Для получения изоклин необходимо положить Задаем значения константы – C(x, y), и на плоскости строим семейство изоклин. На них под углом к оси абсцисс наносим стрелки. Начальную точку M 0 выбираем произвольно на изоклине C 1 = 0. Из M 0 проводим два y Сi отрезка: под углами и до пересечения с соседней изоклиной C 2. Точки x пересечения отрезков с изоклиной - M 1′ и M 1′′. С 1=0 Точка фазовой траектории - точка M 1, С 2

МЕТОД ПРИПАСОВЫВАНИЯ применяется для АСУ, где линейная часть 2 -го порядка, а нелинейная часть - имеет кусочнолинейную статическую характеристику. Этапы построения фазовой траектории по частям с линейными участками статической характеристики: 1) выбираются или задаются начальные условия; 2) интегрируется система линейных уравнений для того линейного участка статической характеристики, на который попали начальные условия, до момента выхода на границу следующего участка; 3) выполняется припасовывание начальных условий: значения фазовых координат в конце участка траектории принимаются начальными условиями для решения уравнения на следующем участке. Граница между участками называется линией переключения.

МЕТОД СШИВАНИЯ аналогичен методу припасовывания и применим в тех же ситуациях. Кусочно-линейная характеристика разбивается на линейные участки, для которых строится своя фазовая траектория и определяется некоторая область фазового пространства. Общий фазовый портрет получается "сшиванием" отдельных областей желаемым образом. При переходе через границы этих установленных областей АСУ изменяет свою структуру. Метод используется при построении фазовых портретов АСУ с переменной структурой (например: релейные АСУ, замыкающие или размыкающие часть схемы при переходе через линии сшивания и позволяющие при определенных условиях получить виды движения более высокого качества, чем в любой из отдельно взятых структур).