Нелинейное программирование Задачами нелинейного программирования (НЛП) называются задачи,




![Методы исключения интервалов Правило исключения интервалов Пусть W(x) унимодальна на отрезке [a,b], а ее Методы исключения интервалов Правило исключения интервалов Пусть W(x) унимодальна на отрезке [a,b], а ее](https://present5.com/customparser/5742174_17870803 --- tpr_04_boo.ppt/slide_5.jpg)


![Методы исключения интервалов Метод золотого сечения Поиск минимума на участке [a,b]. Шаг 1. x1=a+(1-K)(b-a). Методы исключения интервалов Метод золотого сечения Поиск минимума на участке [a,b]. Шаг 1. x1=a+(1-K)(b-a).](https://present5.com/customparser/5742174_17870803 --- tpr_04_boo.ppt/slide_8.jpg)



tpr_04_boo.ppt
- Количество слайдов: 14
 Нелинейное программирование Задачами нелинейного программирования (НЛП) называются задачи, в которых нелинейны и (или) целевая функция, и (или) ограничения в виде равенств и неравенств и для которых методы математического анализа оказываются непригодными. Задачи НЛП можно классифицировать в соответствии с видом функций W(x), hk(x), gj(x) и размерностью и содержанием вектора x.
Нелинейное программирование Задачами нелинейного программирования (НЛП) называются задачи, в которых нелинейны и (или) целевая функция, и (или) ограничения в виде равенств и неравенств и для которых методы математического анализа оказываются непригодными. Задачи НЛП можно классифицировать в соответствии с видом функций W(x), hk(x), gj(x) и размерностью и содержанием вектора x.
 Безусловная однопарам. оптим-я Группы методов БОО: методы случайного поиска методы исключения интервалов методы полиномиальной аппроксимации методы с использованием производных
Безусловная однопарам. оптим-я Группы методов БОО: методы случайного поиска методы исключения интервалов методы полиномиальной аппроксимации методы с использованием производных
 Метод случайного поиска Метод случайного поиска основан на последовательной случайной генерации достаточно большого количества значений в промежутке нахождения корня с последующим сужением этого промежутка. Алгоритм метода случайного поиска На промежутке [a,b] с помощью генератора случайных чисел образуется массив из N значений независимой переменной и функции (N>100). Среди элементов массива значений функции находится оптимальное значение (Wmin, Wmax), а также соответствующее ему значение переменной (xmin, xmax). Рассчитывается новый промежуток, в пределах которого будет производиться последующий выбор из N значений. Например, для уменьшения промежутка процентов на 10%, L=0.9*(b-a); a_new=x_optimal – L/2; if a_newb then b_new=b; a b x_opt b_new a_new
Метод случайного поиска Метод случайного поиска основан на последовательной случайной генерации достаточно большого количества значений в промежутке нахождения корня с последующим сужением этого промежутка. Алгоритм метода случайного поиска На промежутке [a,b] с помощью генератора случайных чисел образуется массив из N значений независимой переменной и функции (N>100). Среди элементов массива значений функции находится оптимальное значение (Wmin, Wmax), а также соответствующее ему значение переменной (xmin, xmax). Рассчитывается новый промежуток, в пределах которого будет производиться последующий выбор из N значений. Например, для уменьшения промежутка процентов на 10%, L=0.9*(b-a); a_new=x_optimal – L/2; if a_newb then b_new=b; a b x_opt b_new a_new
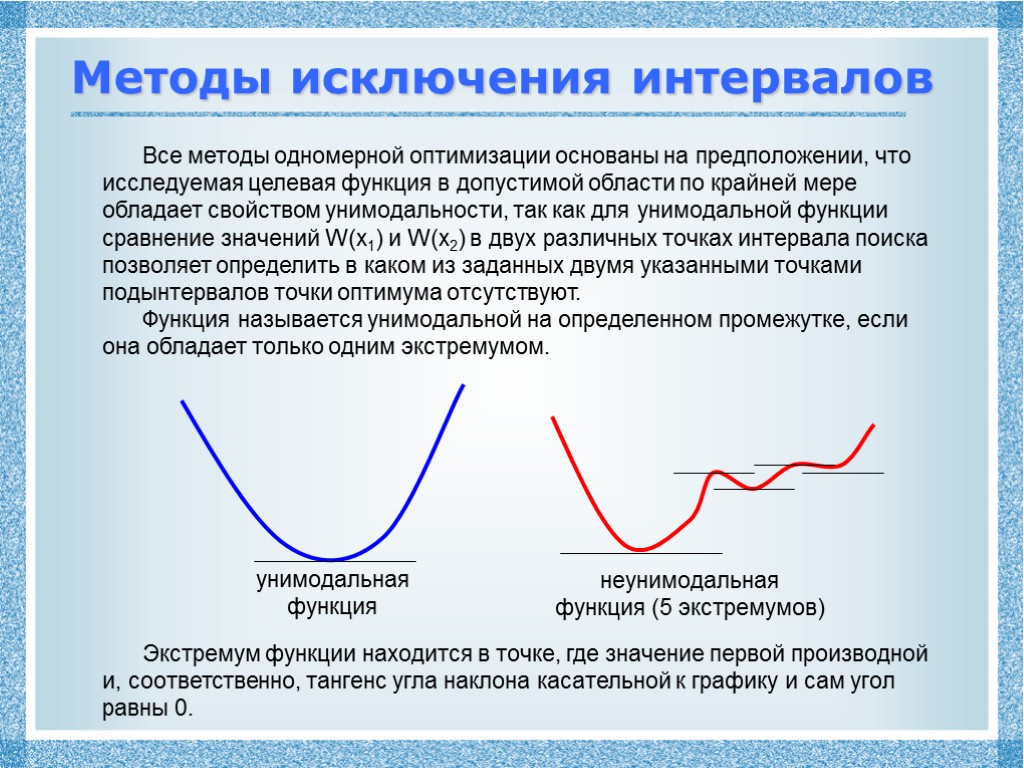
 Методы исключения интервалов Все методы одномерной оптимизации основаны на предположении, что исследуемая целевая функция в допустимой области по крайней мере обладает свойством унимодальности, так как для унимодальной функции сравнение значений W(x1) и W(x2) в двух различных точках интервала поиска позволяет определить в каком из заданных двумя указанными точками подынтервалов точки оптимума отсутствуют. Функция называется унимодальной на определенном промежутке, если она обладает только одним экстремумом. унимодальная функция неунимодальная функция (5 экстремумов) Экстремум функции находится в точке, где значение первой производной и, соответственно, тангенс угла наклона касательной к графику и сам угол равны 0.
Методы исключения интервалов Все методы одномерной оптимизации основаны на предположении, что исследуемая целевая функция в допустимой области по крайней мере обладает свойством унимодальности, так как для унимодальной функции сравнение значений W(x1) и W(x2) в двух различных точках интервала поиска позволяет определить в каком из заданных двумя указанными точками подынтервалов точки оптимума отсутствуют. Функция называется унимодальной на определенном промежутке, если она обладает только одним экстремумом. унимодальная функция неунимодальная функция (5 экстремумов) Экстремум функции находится в точке, где значение первой производной и, соответственно, тангенс угла наклона касательной к графику и сам угол равны 0.
![>Методы исключения интервалов Правило исключения интервалов Пусть W(x) унимодальна на отрезке [a,b], а ее >Методы исключения интервалов Правило исключения интервалов Пусть W(x) унимодальна на отрезке [a,b], а ее](https://present5.com/customparser/5742174_17870803 --- tpr_04_boo.ppt/slide_5.jpg) Методы исключения интервалов Правило исключения интервалов Пусть W(x) унимодальна на отрезке [a,b], а ее минимум достигается в точке x*. Рассмотрим x1 и x2, расположенные a
Методы исключения интервалов Правило исключения интервалов Пусть W(x) унимодальна на отрезке [a,b], а ее минимум достигается в точке x*. Рассмотрим x1 и x2, расположенные a
 Методы исключения интервалов Процесс применения методов поиска на основе исключения интервалов включает два этапа: этап установления границ интервала; этап уменьшения интервала. 1. Этап установления границ интервала, метод Свенна Выбирается исходная точка, а затем на основе правила исключения строится относительно широкий интервал, содержащий точку оптимума. (k+1) пробная точка определяется по рекуррентной формуле xk+1= xk+2k , k=0,1,2... x0 – произвольная точка, - подбираемая величина шага. В случае поиска минимума функции знак определяется путем сравнения значений W(x0), W(x0+||), W(x0-||): если W(x0-||) W(x0) W(x0+||), то >0; если W(x0-||) W(x0) W(x0+||), то <0; если W(x0-||) W(x0) W(x0+||), то точка минимума лежит между (x0-||) и (x0+||) и поиск граничных точек завершен; если W(x0-||) W(x0) W(x0+||), то имеем противоречие предположению об унимодальности.
Методы исключения интервалов Процесс применения методов поиска на основе исключения интервалов включает два этапа: этап установления границ интервала; этап уменьшения интервала. 1. Этап установления границ интервала, метод Свенна Выбирается исходная точка, а затем на основе правила исключения строится относительно широкий интервал, содержащий точку оптимума. (k+1) пробная точка определяется по рекуррентной формуле xk+1= xk+2k , k=0,1,2... x0 – произвольная точка, - подбираемая величина шага. В случае поиска минимума функции знак определяется путем сравнения значений W(x0), W(x0+||), W(x0-||): если W(x0-||) W(x0) W(x0+||), то >0; если W(x0-||) W(x0) W(x0+||), то <0; если W(x0-||) W(x0) W(x0+||), то точка минимума лежит между (x0-||) и (x0+||) и поиск граничных точек завершен; если W(x0-||) W(x0) W(x0+||), то имеем противоречие предположению об унимодальности.
 Методы исключения интервалов Пример установления границ интервала W(x)=(100-x)2, x0=30, ||=5, найти границы поиска минимума функции. W(30-5)=5625, W(30)=4900, W(30+5)=4225, сл. >0. x1=x0+*20=35, W(x1)=4225 x2=x1+*21=45, W(x2)=3025 < W(x1), сл. x*>35 x3=x2+*22=65, W(x3)=1225 < W(x2), сл. x*>45 x4=x3+*23=105, W(x4)=25 < W(x3), сл. x*>65 x5=x4+*24=185, W(x5)=7225 > W(x4), сл. x*<185 Искомый интервал поиска корня: 65 < x* < 185 2. Этап уменьшения интервала Метод деления отрезка пополам (поиск минимума) Шаг 1. xm=(a+b)/2; L=b-a; вычислить W(xm). Шаг 2. x1=a+L/4; x2=b-L/4; вычислить W(x1) и W(x2). Шаг 3. If W(x1)
Методы исключения интервалов Пример установления границ интервала W(x)=(100-x)2, x0=30, ||=5, найти границы поиска минимума функции. W(30-5)=5625, W(30)=4900, W(30+5)=4225, сл. >0. x1=x0+*20=35, W(x1)=4225 x2=x1+*21=45, W(x2)=3025 < W(x1), сл. x*>35 x3=x2+*22=65, W(x3)=1225 < W(x2), сл. x*>45 x4=x3+*23=105, W(x4)=25 < W(x3), сл. x*>65 x5=x4+*24=185, W(x5)=7225 > W(x4), сл. x*<185 Искомый интервал поиска корня: 65 < x* < 185 2. Этап уменьшения интервала Метод деления отрезка пополам (поиск минимума) Шаг 1. xm=(a+b)/2; L=b-a; вычислить W(xm). Шаг 2. x1=a+L/4; x2=b-L/4; вычислить W(x1) и W(x2). Шаг 3. If W(x1)
![>Методы исключения интервалов Метод золотого сечения Поиск минимума на участке [a,b]. Шаг 1. x1=a+(1-K)(b-a). >Методы исключения интервалов Метод золотого сечения Поиск минимума на участке [a,b]. Шаг 1. x1=a+(1-K)(b-a).](https://present5.com/customparser/5742174_17870803 --- tpr_04_boo.ppt/slide_8.jpg) Методы исключения интервалов Метод золотого сечения Поиск минимума на участке [a,b]. Шаг 1. x1=a+(1-K)(b-a). Шаг 2. x2=a+K(b-a). Шаг 3. If |x1 - x2|
Методы исключения интервалов Метод золотого сечения Поиск минимума на участке [a,b]. Шаг 1. x1=a+(1-K)(b-a). Шаг 2. x2=a+K(b-a). Шаг 3. If |x1 - x2|
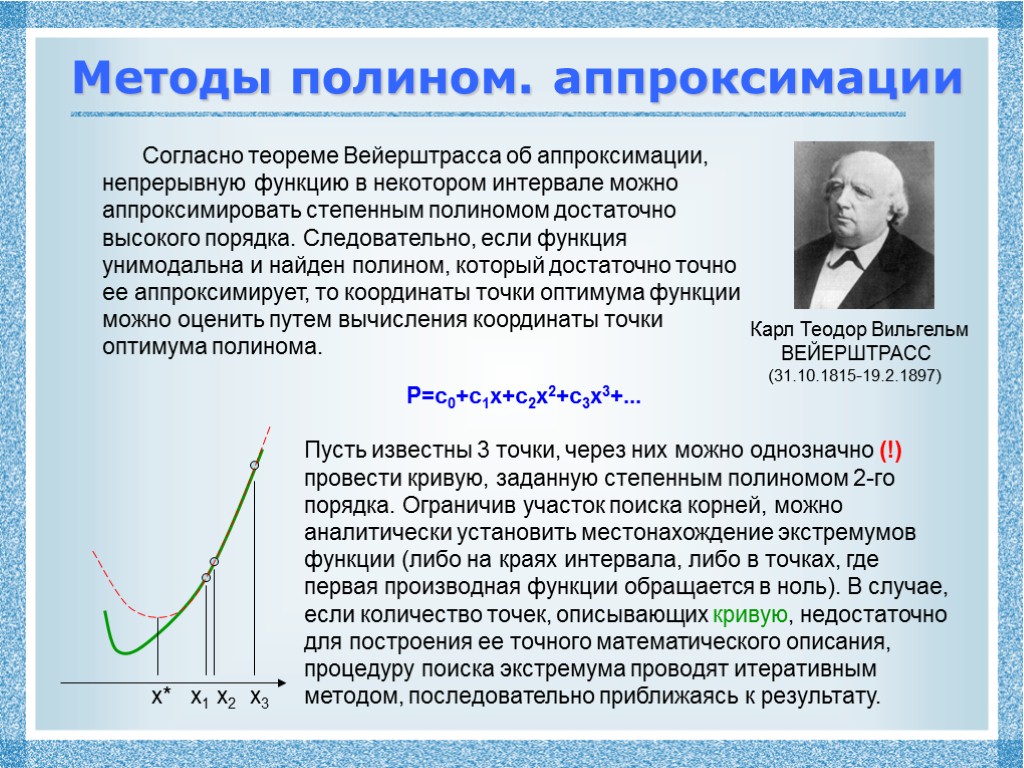
 Методы полином. аппроксимации Карл Теодор Вильгельм ВЕЙЕРШТРАСС (31.10.1815-19.2.1897) Согласно теореме Вейерштрасса об аппроксимации, непрерывную функцию в некотором интервале можно аппроксимировать степенным полиномом достаточно высокого порядка. Следовательно, если функция унимодальна и найден полином, который достаточно точно ее аппроксимирует, то координаты точки оптимума функции можно оценить путем вычисления координаты точки оптимума полинома. P=c0+c1x+c2x2+c3x3+... Пусть известны 3 точки, через них можно однозначно (!) провести кривую, заданную степенным полиномом 2-го порядка. Ограничив участок поиска корней, можно аналитически установить местонахождение экстремумов функции (либо на краях интервала, либо в точках, где первая производная функции обращается в ноль). В случае, если количество точек, описывающих кривую, недостаточно для построения ее точного математического описания, процедуру поиска экстремума проводят итеративным методом, последовательно приближаясь к результату. x* x1 x2 x3
Методы полином. аппроксимации Карл Теодор Вильгельм ВЕЙЕРШТРАСС (31.10.1815-19.2.1897) Согласно теореме Вейерштрасса об аппроксимации, непрерывную функцию в некотором интервале можно аппроксимировать степенным полиномом достаточно высокого порядка. Следовательно, если функция унимодальна и найден полином, который достаточно точно ее аппроксимирует, то координаты точки оптимума функции можно оценить путем вычисления координаты точки оптимума полинома. P=c0+c1x+c2x2+c3x3+... Пусть известны 3 точки, через них можно однозначно (!) провести кривую, заданную степенным полиномом 2-го порядка. Ограничив участок поиска корней, можно аналитически установить местонахождение экстремумов функции (либо на краях интервала, либо в точках, где первая производная функции обращается в ноль). В случае, если количество точек, описывающих кривую, недостаточно для построения ее точного математического описания, процедуру поиска экстремума проводят итеративным методом, последовательно приближаясь к результату. x* x1 x2 x3
 Метод квадратич. аппроксимации Простейший случай полиномиальной аппроксимации основан на том факте, что функция, принимающая минимальное (максимальное) значение во внутренней точке интервала, должна быть по крайней мере квадратичной. Если целевая функция W(x) в точках x1, x2, x3 принимает соответствующие значения W1, W2, W3, то можно определить коэффициенты a0, a1, a2 таким образом, что значения квадратичной функции q(x) = a0 + a1(x-x1) + a2(x-x1)(x-x2) совпадут со значением W(x) в трех указанных точках. Вычислим q(x) в трех указанных точках. W1=W(x1)=q(x1)=a0 a0=W1 W2=W(x2)=q(x2)=W1+a1(x2-x1) a1=(W2-W1)/(x2-x1) W3=q(x3)=W1+(W2-W1)(x3-x1)/(x2-x1)+a2(x3-x1)(x3-x2) a2=[(W3-W1)/(x3-x1) - (W2-W1)/(x2-x1)]/(x3-x2) dq/dx=0 q'(x)=a1+2a2x-a2x1-a2x2=0 x*=1/2*(x1+x2-a1/a2) (*)
Метод квадратич. аппроксимации Простейший случай полиномиальной аппроксимации основан на том факте, что функция, принимающая минимальное (максимальное) значение во внутренней точке интервала, должна быть по крайней мере квадратичной. Если целевая функция W(x) в точках x1, x2, x3 принимает соответствующие значения W1, W2, W3, то можно определить коэффициенты a0, a1, a2 таким образом, что значения квадратичной функции q(x) = a0 + a1(x-x1) + a2(x-x1)(x-x2) совпадут со значением W(x) в трех указанных точках. Вычислим q(x) в трех указанных точках. W1=W(x1)=q(x1)=a0 a0=W1 W2=W(x2)=q(x2)=W1+a1(x2-x1) a1=(W2-W1)/(x2-x1) W3=q(x3)=W1+(W2-W1)(x3-x1)/(x2-x1)+a2(x3-x1)(x3-x2) a2=[(W3-W1)/(x3-x1) - (W2-W1)/(x2-x1)]/(x3-x2) dq/dx=0 q'(x)=a1+2a2x-a2x1-a2x2=0 x*=1/2*(x1+x2-a1/a2) (*)
 Метод квадратич. аппроксимации Метод Пауэлла Шаг 1. x2 = x1 + x. Шаг 2. Вычислить W(x1) и W(x2). Шаг 3. Для поиска минимума Если W(x1) > W(x2), то x3 = x1 + 2x. Если W(x1) W(x2), то x3 = x1 - x. Шаг 4. Вычислить W(x3) и найти Wmin=min {W(x1),W(x2), W(x3)}, xmin=xi, соответствующая Wmin. Шаг 5. По x1, x2, x3 вычислить x*, используя формулу (*) для оценивания с помощью квадратической аппроксимации. Шаг 6. Проверка окончания Если |Wmin - W(x*)| < eW, то закончить поиск. В противном случае к шагу 7. Если |xmin - x*| < ex, то закончить поиск. В противном случае к шагу 7. Шаг 7. Выбрать xmin или x* и две точки по обе стороны от нее. Обозначить в естественном порядке и перейти к шагу 4.
Метод квадратич. аппроксимации Метод Пауэлла Шаг 1. x2 = x1 + x. Шаг 2. Вычислить W(x1) и W(x2). Шаг 3. Для поиска минимума Если W(x1) > W(x2), то x3 = x1 + 2x. Если W(x1) W(x2), то x3 = x1 - x. Шаг 4. Вычислить W(x3) и найти Wmin=min {W(x1),W(x2), W(x3)}, xmin=xi, соответствующая Wmin. Шаг 5. По x1, x2, x3 вычислить x*, используя формулу (*) для оценивания с помощью квадратической аппроксимации. Шаг 6. Проверка окончания Если |Wmin - W(x*)| < eW, то закончить поиск. В противном случае к шагу 7. Если |xmin - x*| < ex, то закончить поиск. В противном случае к шагу 7. Шаг 7. Выбрать xmin или x* и две точки по обе стороны от нее. Обозначить в естественном порядке и перейти к шагу 4.
 Методы с исполь-ем производных Требования: непрерывность и дифференцируемость функции. Метод средней точки Основан на алгоритме исключения интервалов, на каждой итерации которого рассматривается одна пробная точка R. Если в точке R выполняется неравенство W'(R) < 0 (W(R) убывает), то вследствие унимодальности функции точка оптимума (минимума в данном случае) не может лежать левее точки R. Аналогично, если W'(R) > 0, то интервал x>R можно исключить. Пусть в интервале [a,b] имеются две точки N и P, в которых производные W'(N)<0 и W'(P)>0. Оптимальная точка (минимум функции W(x)) x* расположена между N и P. x W'(x) N R P x* Шаг 1. Положить P=b, N=a, причем W'(a)<0 и W'(b)>0. Шаг 2. Вычислить R=(P+N)/2 и W'(R). Шаг 3. Если |W'(R)| < e , то закончить поиск. В противном случае, если W'(R)<0, положить N=R, и перейти к шагу 2. Если | W'(R)| > e , положить P=R и перейти к шагу 2.
Методы с исполь-ем производных Требования: непрерывность и дифференцируемость функции. Метод средней точки Основан на алгоритме исключения интервалов, на каждой итерации которого рассматривается одна пробная точка R. Если в точке R выполняется неравенство W'(R) < 0 (W(R) убывает), то вследствие унимодальности функции точка оптимума (минимума в данном случае) не может лежать левее точки R. Аналогично, если W'(R) > 0, то интервал x>R можно исключить. Пусть в интервале [a,b] имеются две точки N и P, в которых производные W'(N)<0 и W'(P)>0. Оптимальная точка (минимум функции W(x)) x* расположена между N и P. x W'(x) N R P x* Шаг 1. Положить P=b, N=a, причем W'(a)<0 и W'(b)>0. Шаг 2. Вычислить R=(P+N)/2 и W'(R). Шаг 3. Если |W'(R)| < e , то закончить поиск. В противном случае, если W'(R)<0, положить N=R, и перейти к шагу 2. Если | W'(R)| > e , положить P=R и перейти к шагу 2.
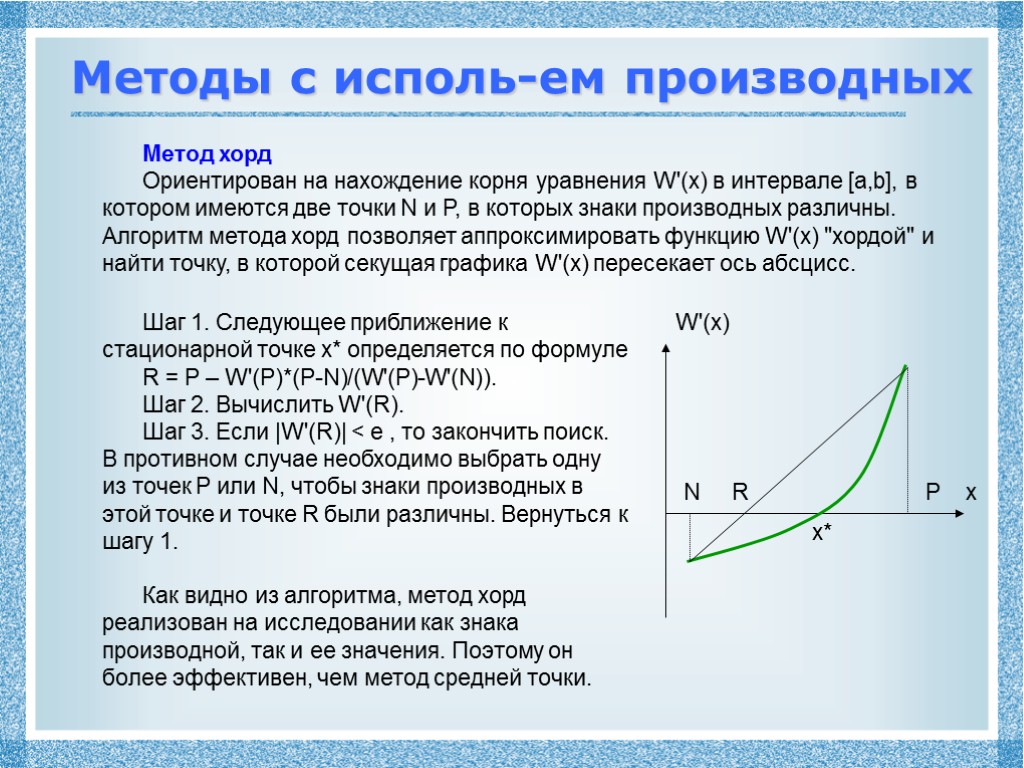
 Методы с исполь-ем производных Метод хорд Ориентирован на нахождение корня уравнения W'(x) в интервале [a,b], в котором имеются две точки N и P, в которых знаки производных различны. Алгоритм метода хорд позволяет аппроксимировать функцию W'(x) "хордой" и найти точку, в которой секущая графика W'(x) пересекает ось абсцисс. Шаг 1. Следующее приближение к стационарной точке x* определяется по формуле R = P – W'(P)*(P-N)/(W'(P)-W'(N)). Шаг 2. Вычислить W'(R). Шаг 3. Если |W'(R)| < e , то закончить поиск. В противном случае необходимо выбрать одну из точек P или N, чтобы знаки производных в этой точке и точке R были различны. Вернуться к шагу 1. Как видно из алгоритма, метод хорд реализован на исследовании как знака производной, так и ее значения. Поэтому он более эффективен, чем метод средней точки. x W'(x) N R P x*
Методы с исполь-ем производных Метод хорд Ориентирован на нахождение корня уравнения W'(x) в интервале [a,b], в котором имеются две точки N и P, в которых знаки производных различны. Алгоритм метода хорд позволяет аппроксимировать функцию W'(x) "хордой" и найти точку, в которой секущая графика W'(x) пересекает ось абсцисс. Шаг 1. Следующее приближение к стационарной точке x* определяется по формуле R = P – W'(P)*(P-N)/(W'(P)-W'(N)). Шаг 2. Вычислить W'(R). Шаг 3. Если |W'(R)| < e , то закончить поиск. В противном случае необходимо выбрать одну из точек P или N, чтобы знаки производных в этой точке и точке R были различны. Вернуться к шагу 1. Как видно из алгоритма, метод хорд реализован на исследовании как знака производной, так и ее значения. Поэтому он более эффективен, чем метод средней точки. x W'(x) N R P x*
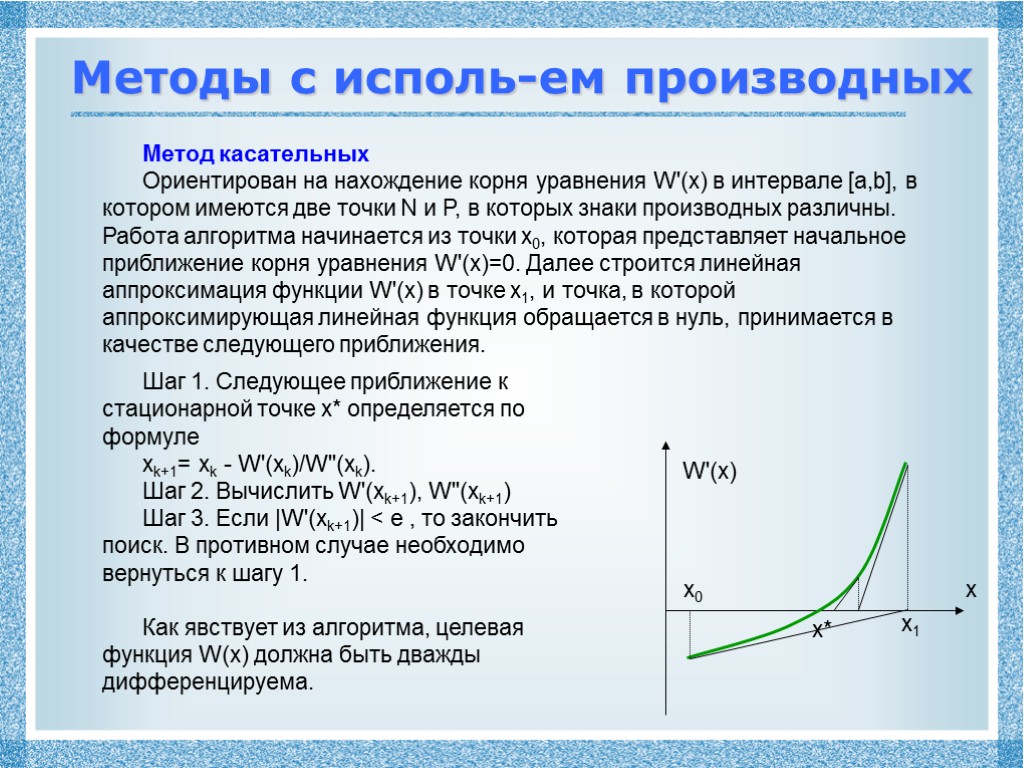
 Методы с исполь-ем производных Метод касательных Ориентирован на нахождение корня уравнения W'(x) в интервале [a,b], в котором имеются две точки N и P, в которых знаки производных различны. Работа алгоритма начинается из точки x0, которая представляет начальное приближение корня уравнения W'(x)=0. Далее строится линейная аппроксимация функции W'(x) в точке x1, и точка, в которой аппроксимирующая линейная функция обращается в нуль, принимается в качестве следующего приближения. Шаг 1. Следующее приближение к стационарной точке x* определяется по формуле xk+1= xk - W'(xk)/W''(xk). Шаг 2. Вычислить W'(xk+1), W''(xk+1) Шаг 3. Если |W'(xk+1)| < e , то закончить поиск. В противном случае необходимо вернуться к шагу 1. Как явствует из алгоритма, целевая функция W(x) должна быть дважды дифференцируема. x W'(x) x0 x1 x*
Методы с исполь-ем производных Метод касательных Ориентирован на нахождение корня уравнения W'(x) в интервале [a,b], в котором имеются две точки N и P, в которых знаки производных различны. Работа алгоритма начинается из точки x0, которая представляет начальное приближение корня уравнения W'(x)=0. Далее строится линейная аппроксимация функции W'(x) в точке x1, и точка, в которой аппроксимирующая линейная функция обращается в нуль, принимается в качестве следующего приближения. Шаг 1. Следующее приближение к стационарной точке x* определяется по формуле xk+1= xk - W'(xk)/W''(xk). Шаг 2. Вычислить W'(xk+1), W''(xk+1) Шаг 3. Если |W'(xk+1)| < e , то закончить поиск. В противном случае необходимо вернуться к шагу 1. Как явствует из алгоритма, целевая функция W(x) должна быть дважды дифференцируема. x W'(x) x0 x1 x*

