Скачать презентацию Нелинейная регрессия Один из недостатков линейного регрессионного Скачать презентацию Нелинейная регрессия Один из недостатков линейного регрессионного

8 Нелинейная регрессия.ppt

  • Количество слайдов: 52

Нелинейная регрессия Нелинейная регрессия

Один из недостатков линейного регрессионного анализа состоит в том, что он может быть применен Один из недостатков линейного регрессионного анализа состоит в том, что он может быть применен только к линейным уравнениям. n Очень часто зависимости между экономическими факторами являются нелинейными n Уравнения являются нелинейными

n n n Нелинейность по переменным всегда можно свести к линейной путём использования соответствующих n n n Нелинейность по переменным всегда можно свести к линейной путём использования соответствующих определений. Например, предположим, что соотношение имеет вид: y=α+βx 2 Если определить z= x 2 , то уравнение y=α+βz будет линейным

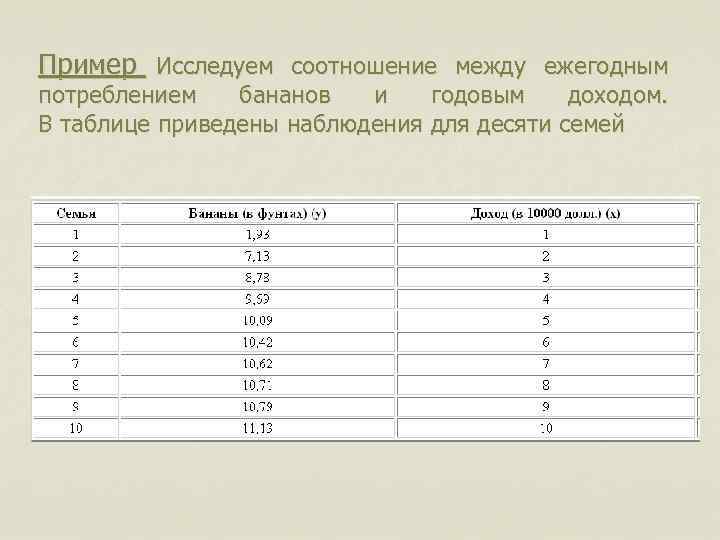Пример Исследуем соотношение между ежегодным потреблением бананов и годовым доходом. В таблице приведены наблюдения Пример Исследуем соотношение между ежегодным потреблением бананов и годовым доходом. В таблице приведены наблюдения для десяти семей

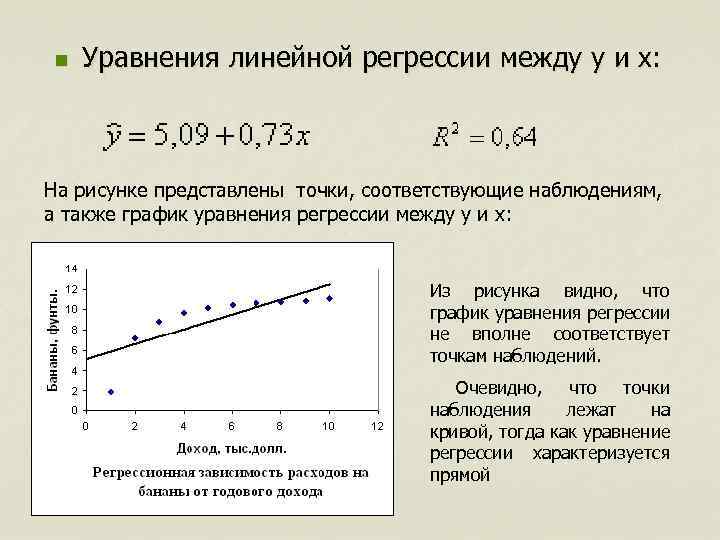n Уравнения линейной регрессии между y и x: На рисунке представлены точки, соответствующие наблюдениям, n Уравнения линейной регрессии между y и x: На рисунке представлены точки, соответствующие наблюдениям, а также график уравнения регрессии между y и x: Из рисунка видно, что график уравнения регрессии не вполне соответствует точкам наблюдений. Очевидно, что точки наблюдения лежат на кривой, тогда как уравнение регрессии характеризуется прямой

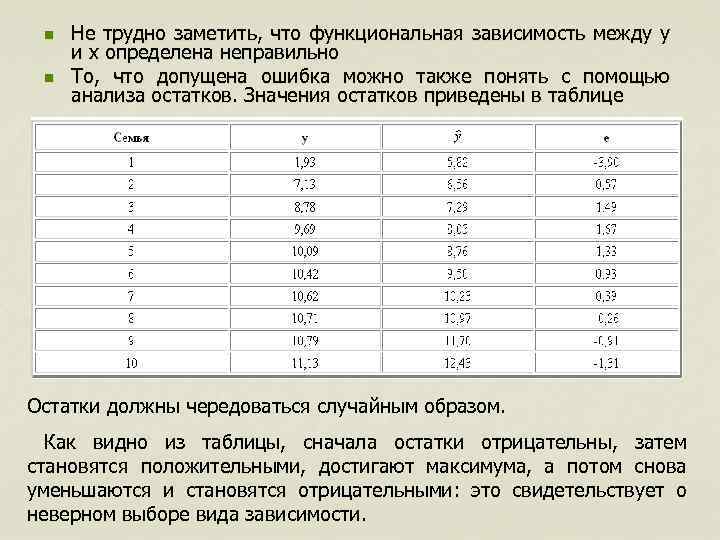n n Не трудно заметить, что функциональная зависимость между y и x определена неправильно n n Не трудно заметить, что функциональная зависимость между y и x определена неправильно То, что допущена ошибка можно также понять с помощью анализа остатков. Значения остатков приведены в таблице Остатки должны чередоваться случайным образом. Как видно из таблицы, сначала остатки отрицательны, затем становятся положительными, достигают максимума, а потом снова уменьшаются и становятся отрицательными: это свидетельствует о неверном выборе вида зависимости.

n Предполагаем, что истинное соотношение имеет вид Если мы знаем это и определим то n Предполагаем, что истинное соотношение имеет вид Если мы знаем это и определим то уравнение примет линейный вид

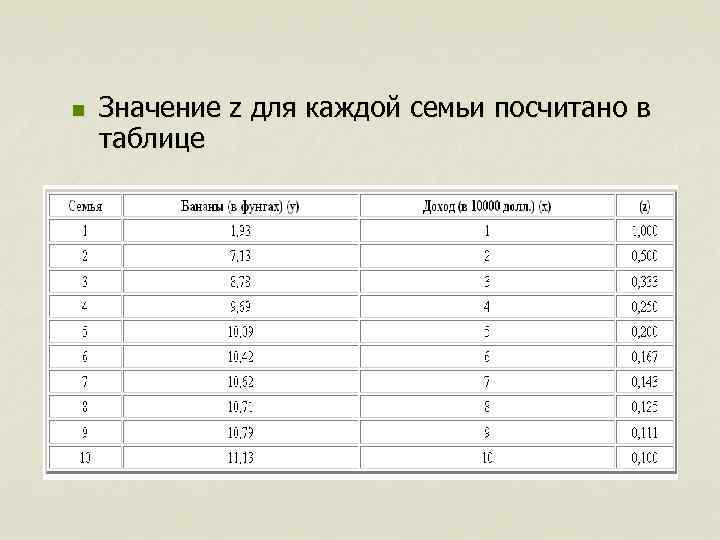n Значение z для каждой семьи посчитано в таблице n Значение z для каждой семьи посчитано в таблице

Оценив регрессию между y и z, получим Подставив имеем: Оценив регрессию между y и z, получим Подставив имеем:

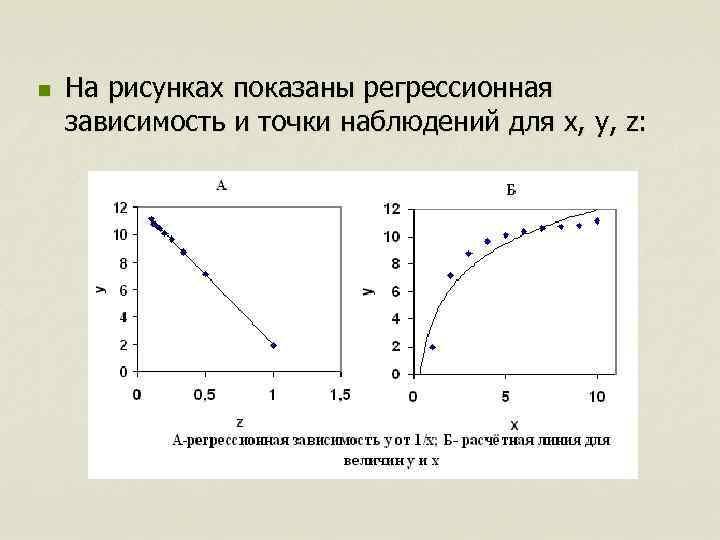n На рисунках показаны регрессионная зависимость и точки наблюдений для x, y, z: n На рисунках показаны регрессионная зависимость и точки наблюдений для x, y, z:

Логарифмические преобразования n Рассмотрим функции, которые являются нелинейными как по параметрам, так и по Логарифмические преобразования n Рассмотрим функции, которые являются нелинейными как по параметрам, так и по переменным q. Это соотношение может быть преобразовано в линейное уравнение путем логарифмирования обеих частей соотношения.

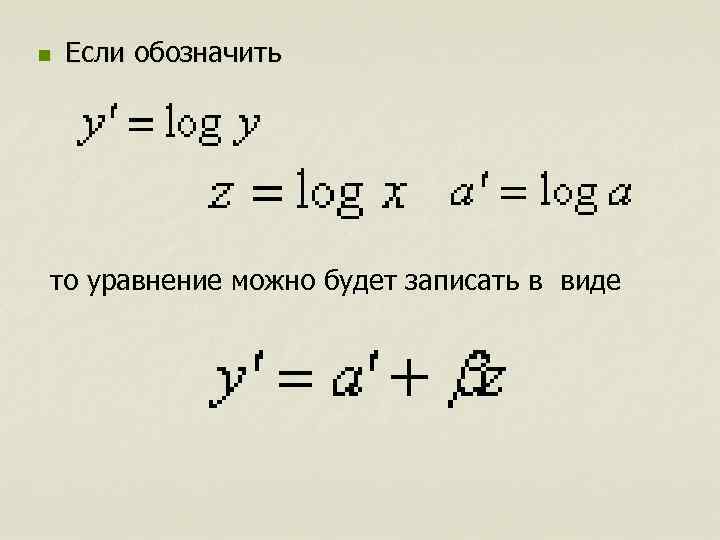n Если обозначить то уравнение можно будет записать в виде n Если обозначить то уравнение можно будет записать в виде

Процедура оценивания регрессии будет следующей. n С начала вычислим y’ и z для каждого Процедура оценивания регрессии будет следующей. n С начала вычислим y’ и z для каждого наблюдения с помощью логарифмов от исходных значений. n Затем оценим регрессионную зависимость y’ от z. n Коэффициент при z будет представлять собой непосредственно оценку β. Постоянный член является оценкой ά. n Для получения оценки необходимо взять антилогарифм, т. е. , вычислить.

Моделирование эластичности n n n Функции этого вида часто встречаются в экономике. Эта общая Моделирование эластичности n n n Функции этого вида часто встречаются в экономике. Эта общая форма кривых Энгеля, y представляет собой спрос на товар, x-доход, а β-эластичность спроса по доходу. Докажем указанное свойство эластичности.

n Независимо от математической связи между y и x или определения величин y и n Независимо от математической связи между y и x или определения величин y и x, эластичность y по x рассчитывается как относительное изменение y на единицу относительного изменения x: Таким образом, если y-это спрос, а х- доход, то выражение определяет эластичность спроса на данный товар по доходу.

n Выражение для эластичность можно переписать в следующем виде С функцией спроса его можно n Выражение для эластичность можно переписать в следующем виде С функцией спроса его можно представить как соотношение предельной склонности к потреблению товара к средней склонности к потреблению данного товара.

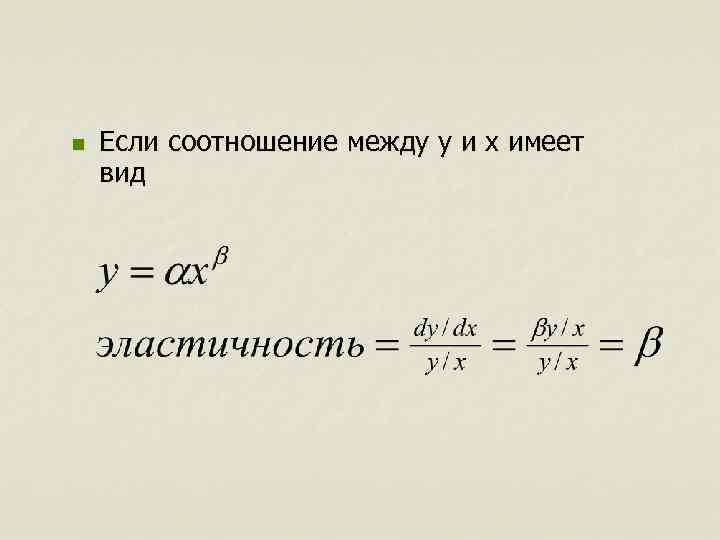n Если соотношение между y и x имеет вид n Если соотношение между y и x имеет вид

n Таким образом, если имеется кривая Энгеля вида , nэто означает, что эластичность спроса n Таким образом, если имеется кривая Энгеля вида , nэто означает, что эластичность спроса по доходу = 0, 3.

Функция этого вида может также применяться к кривым спроса, где y- спрос на товар, Функция этого вида может также применяться к кривым спроса, где y- спрос на товар, х-цена товара, β - эластичность спроса по цене. n

Что произойдёт, если математическая связь между y и x будет другая. n Предположим, имеется Что произойдёт, если математическая связь между y и x будет другая. n Предположим, имеется обычное линейное уравнение y=α+βx следовательно эластичность определяется следующим образом: n В этом случае значение эластичности в любой точке будет зависеть не только от значения β , но также от значений y и x.

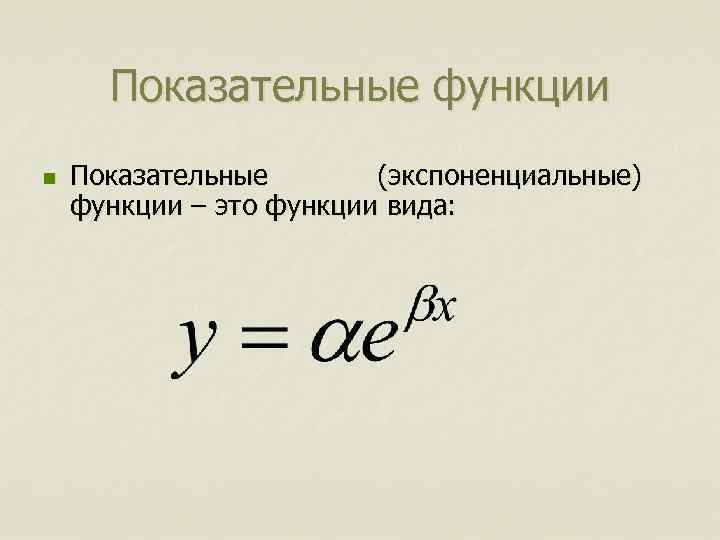Показательные функции n Показательные (экспоненциальные) функции – это функции вида: Показательные функции n Показательные (экспоненциальные) функции – это функции вида:

n Наиболее общим их приложением является случай, когда предполагается, что переменная y имеет постоянный n Наиболее общим их приложением является случай, когда предполагается, что переменная y имеет постоянный темп прироста во времени, в этом случае вместо х обычно используется время (t), а вместо β - постоянный темп прироста (r):

n Если имеются значения y для нескольких временных периодов(1, …, T), то параметры α n Если имеются значения y для нескольких временных периодов(1, …, T), то параметры α и r можно оценить, если прологарифмировать (по основанию e) обе части уравнения:

n n n Если определить ά=log α и y’=log y , то получим: y’= n n n Если определить ά=log α и y’=log y , то получим: y’= ά+rt Таким образом, оценивая регрессию между логарифмом y и t мы непосредственно получаем оценку темпа прироста r. Обычно оценка имеет второстепенное значение, но если она представляет интерес, то можно получить её, взяв антилогарифм α от ά.

Пример n Кривая Энгеля была построена для расходов на питание в США за период Пример n Кривая Энгеля была построена для расходов на питание в США за период с 1959 по 1983 г.

n n Однако вместо линейной функции в данном случае использовалась не линейная, а приведённая n n Однако вместо линейной функции в данном случае использовалась не линейная, а приведённая к линейному виду, путём логарифмирования. Преобразованное выражение имело вид: Выполнив обратное преобразование, получим:

n n Полученный результат предполагает, что эластичность спроса на продукты питания по доходу составляет n n Полученный результат предполагает, что эластичность спроса на продукты питания по доходу составляет 0, 55 что означает, что увеличение личного располагаемого дохода на 1% приведёт к увеличению расходов на питание на 0, 55%. Коэффициент 3, 32 помогает прогнозировать значения y при заданных значениях x, приводя их к единому масштабу.

Случайный член n n Основное требование состоит в том, чтобы случайный член в преобразованном Случайный член n n Основное требование состоит в том, чтобы случайный член в преобразованном уравнении присутствовал в виде слагаемого и удовлетворял условиям Гаусса-Маркова. В противном случает мы не сможем привести уравнение к линейному виду.

n Например , если исходное уравнение имеет такой вид В этом случае проблем нет, n Например , если исходное уравнение имеет такой вид В этом случае проблем нет, т. к. уравнение преобразуется к линейному путем замены z=1/x и аддитивный случайный член этому не мешает.

n n Если используется модель вида: y=αxβ и мы собираемся преобразовать его к линейному n n Если используется модель вида: y=αxβ и мы собираемся преобразовать его к линейному путем логарифмирования, то случайный член должен быть мультипликативным y=αxβ v. В этом случае мы получаем соотношение: Следовательно, для получения аддитивного случайного члена в уравнении регрессии мы должны начинать с мультипликативного случайного члена в исходном уравнении.

Нелинейная регрессия. Общий случай n Предположим, что переменная y связана с переменной x следующим Нелинейная регрессия. Общий случай n Предположим, что переменная y связана с переменной x следующим соотношением: и нужно получить оценки α β γ , имея значения y и x. Такое уравнение не может быть преобразовано в уравнение линейного вида. Тем не менее для получения оценок параметров мы можем применить принцип минимизации суммы квадратов отклонений.

n n n Процедура состоит из последовательности шагов. 1. Принимаются некоторые правдоподобные исходные значения n n n Процедура состоит из последовательности шагов. 1. Принимаются некоторые правдоподобные исходные значения параметров. 2. Вычисляются предсказанные значения y по фактическим значениям х с использованием этих значений параметров. 3. Вычисляются остатки для всех наблюдений в выборке и, следовательно, S- сумма квадратов остатков. 4. Вносятся небольшие изменения в одну или более оценку параметров.

n n 5. Вычисляются новые предсказанные значения y, остатки и S. 6. Если S n n 5. Вычисляются новые предсказанные значения y, остатки и S. 6. Если S меньше, чем прежде, то новые оценки параметров лучше прежних и их следует использовать в качестве новой отправной точки.

n n 7. Шаги 4, 5 и 6 повторятся вновь до тех пор, пока n n 7. Шаги 4, 5 и 6 повторятся вновь до тех пор, пока не окажется невозможным внести такие изменения в оценки параметров, которые привели бы к уменьшению S. 8. Делается вывод о том, что величина S минимизирована и конечные оценки параметров являются оценками по методу наименьших квадратов.

Пример n Вернемся к примеру с бананами, где y и x связаны между собой Пример n Вернемся к примеру с бананами, где y и x связаны между собой зависимостью: Предположим, что мы знаем, что α=12 ; значит нам надо определить только один неизвестный параметр. Предположим, что мы поняли, что зависимость имеет вид такой , однако не будем приводить уравнение к линейному виду. Вместо этого мы применяем нелинейную регрессию.

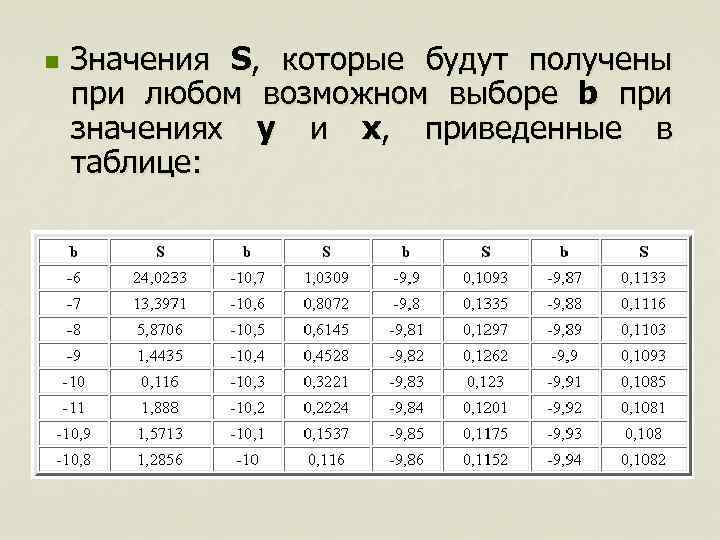n Значения S, которые будут получены при любом возможном выборе b при значениях y n Значения S, которые будут получены при любом возможном выборе b при значениях y и x, приведенные в таблице:

n n Предположим, что мы начнем, приняв b равным -6. Уравнение при этом примет n n Предположим, что мы начнем, приняв b равным -6. Уравнение при этом примет вид:

n n n Вычислим предсказанные значения y и остатки на основании последних вычислим значение n n n Вычислим предсказанные значения y и остатки на основании последних вычислим значение S=24, 02. Затем подставим b=-7. Теперь величина S равна 13, 401, т. е. она уменьшилась. Значит, мы движемся в правильном направлении. Подставим b=-8, тогда S=5, 87. Продолжим дальше. При b=-9 значение S равно 1, 44; при b=-10 значение S составит 0, 12; при b=-11 оно будет 1, 89.

n n n Очевидно, что, выбрав b=-11, мы перестарались, т. к. значение S вновь n n n Очевидно, что, выбрав b=-11, мы перестарались, т. к. значение S вновь начало расти. Будем двигаться назад, но более мелкими шагами, например по 0, 1, беря значение -10, 9; -10, 8 и т. д. Продолжим движение назад до тех пор, пока опять не будет «перебора» , затем вновь начнем двигаться вперед еще более мелкими шагами.

n n Каждый раз, когда будет наблюдаться «перебор» , будем изменять направление на противоположное, n n Каждый раз, когда будет наблюдаться «перебор» , будем изменять направление на противоположное, сокращая размер шага. Будем продолжать делать это до тех пор, пока не достигнем требуемой точности вычисления оценки.

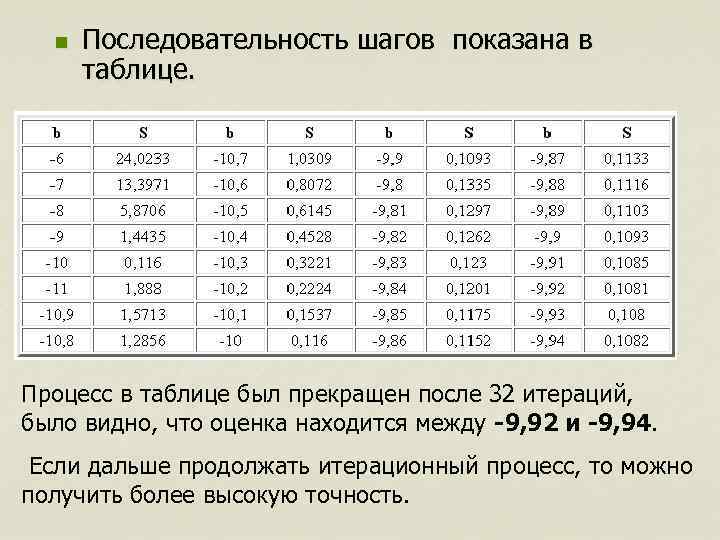n Последовательность шагов показана в таблице. Процесс в таблице был прекращен после 32 итераций, n Последовательность шагов показана в таблице. Процесс в таблице был прекращен после 32 итераций, было видно, что оценка находится между -9, 92 и -9, 94. Если дальше продолжать итерационный процесс, то можно получить более высокую точность.

n Хотя полученная оценка близка к истинному значению 10, она не совпадает с оценкой, n Хотя полученная оценка близка к истинному значению 10, она не совпадает с оценкой, полученной для уравнения Расхождение вызвано тем, что мы предположили, что α=12 , а не оценили его. Если бы мы искали наилучшие значения α и β нелинейным методом, то тогда мы бы получили оценку α = 12, 08, и оценку β= -10, 08.

n Основной недостаток нелинейной регрессии состоит в том, что она оценивается значительно медленнее, чем n Основной недостаток нелинейной регрессии состоит в том, что она оценивается значительно медленнее, чем линейная регрессия, особенно в том случае, когда приходится оценивать несколько параметров.

Выбор функции: тесты Бокса. Кокса n Проблема выбора вида зависимости сложна и если значение Выбор функции: тесты Бокса. Кокса n Проблема выбора вида зависимости сложна и если значение коэффициента детерминации R 2 для разных моделей примерно равны, то проблема выбора может быть решена с помощью теста Бокса –Кокса (Box, Cox 1964)

n n Если сравнивать модели с использованием y и log y в качестве зависимой n n Если сравнивать модели с использованием y и log y в качестве зависимой переменной, то можно использовать вариант теста, разработанный Полом Зарембкой (Zarembka 1968). Этот тест предполагает такое преобразование масштаба наблюдений y, при котором обеспечивалась бы возможность непосредственного сравнения СКО (RSS) в линейной и логарифмических моделях.

n 1. Процедура включает следующие шаги: Вычисляется среднее геометрическое значений y в выборке. n 1. Процедура включает следующие шаги: Вычисляется среднее геометрическое значений y в выборке.

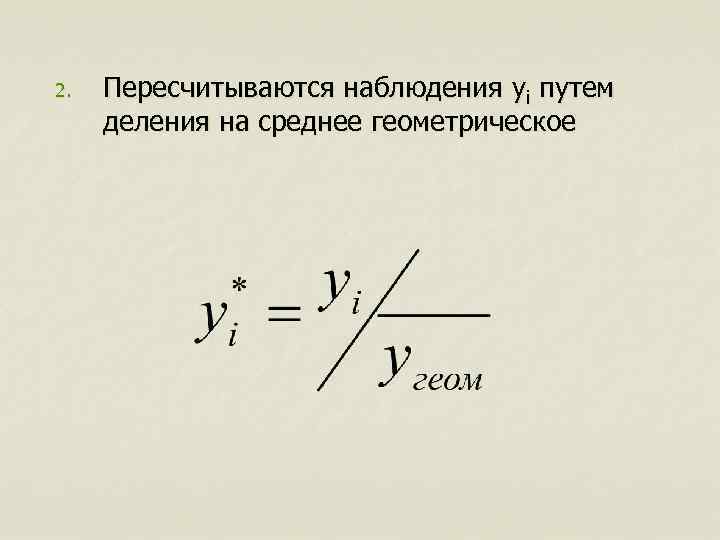2. Пересчитываются наблюдения yi путем деления на среднее геометрическое 2. Пересчитываются наблюдения yi путем деления на среднее геометрическое

Оценивается регрессия для линейной модели с использованием y* и для логарифмической модели с использованием Оценивается регрессия для линейной модели с использованием y* и для логарифмической модели с использованием log(y*). Теперь СКО (RSS) для двух регрессий сравнимы и, следовательно, модель с меньшей суммой квадратов отклонений обеспечивает лучшее соответствие. 3.

Более общий тест Бокса-Кокса n n n Y и log y – это специальные Более общий тест Бокса-Кокса n n n Y и log y – это специальные случаи функции (Yλ-1)/λ , из которой при λ=1 получается функция y , а при λ стремящемся к 0 функция log y. Следует попробовать ряд значений λ, чтобы определить, какое из них дает минимальной значение СКО. Это называется решетчатым поиском.

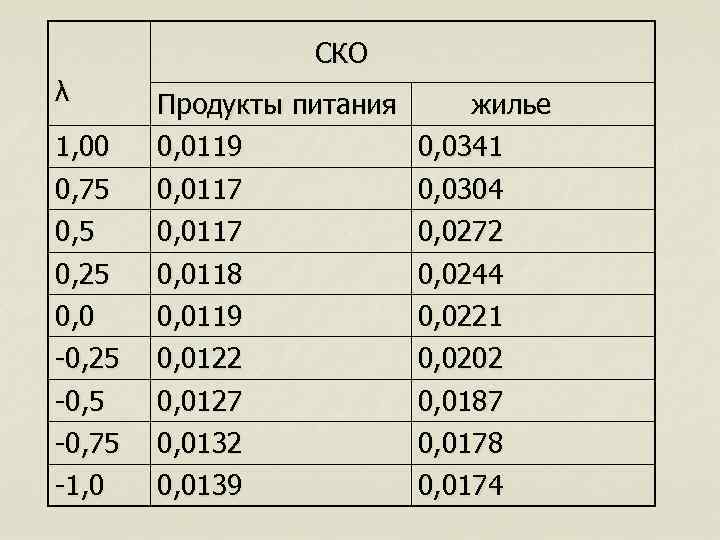СКО λ Продукты питания жилье 1, 00 0, 0119 0, 0341 0, 75 СКО λ Продукты питания жилье 1, 00 0, 0119 0, 0341 0, 75 0, 0117 0, 0304 0, 0272 0, 25 0, 0118 0, 0119 0, 0244 0, 0221 -0, 25 -0, 5 0, 0122 0, 0127 0, 0202 0, 0187 -0, 75 -1, 0 0, 0132 0, 0139 0, 0178 0, 0174

n n В таблице оптимальное значение λ для продуктов питания составляет 0, 5 , n n В таблице оптимальное значение λ для продуктов питания составляет 0, 5 , что говорит о примерно одинаковой приемлемости линейной и логарифмической регрессий. Для расходов на жилье регрессия обратных величин переменных дает более точный прогноз.