Некорректность обратных задач. Множество решений • Геофизические наблюдения можно рассматривать как элемент пространства Y, а модель m – как элемент пространства M. Оператор F преобразует пространство M в пространство Y. Такое преобразование является однозначным. Обратная задача – построение обратного оператора F-1, преобразующего пространство Y в пространство М. Известно, что из-за эквивалентности, обратное преобразование будет неоднозначным. • Основная причина – неполнота реальных геофизических данных: дискретность и ограниченность наблюдений
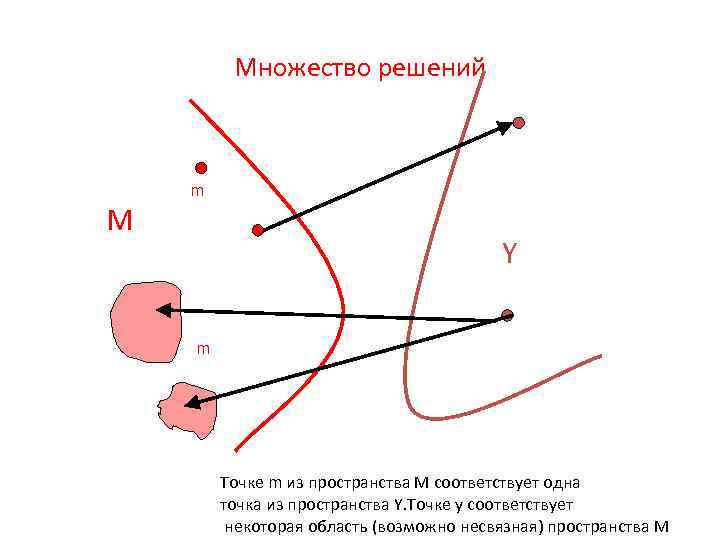
Множество решений M m Y m Точке m из пространства M соответствует одна точка из пространства Y. Точке y соответствует некоторая область (возможно несвязная) пространства M
Множество решений • Что делать? • Выход – найти характеристики, которые определяли все модели, соответствующие области решения. Практически это делается при априорном осреднении характеристик модели (параметризация модели). Чем больше степень осреднения, тем меньше степень эквивалентности. • Проблема! Что происходит при слишком большом осреднении? • Можем получить единственное решение, не соответствующее наблюденным значения. • Что происходит при недостаточном осреднении? Область решения продолжает оставаться слишком большой ПРИ ВЫБОРЕ СПОСОБА ОСРЕДНЕНИЯ НЕОБХОДИМО УЧИТЫВАТЬ ИСХОДНЫЕ НАБЛЮДЕНИЯ
Неустойчивость обратных задач • Оператор преобразования одного пространства в другое называется устойчивым, если малые изменения в исходном пространстве X приводят к малым изменениям в пространстве Y • Оператор решения прямой задачи обычно устойчив • Оператор решения обратной задачи обычно неустойчив: следовательно малые изменения исходных данных могут приводить к сколь угодно большим изменениям в модели m. Наблюдения y всегда имеют ошибку. • Наблюдения геофизических полей всегда содержат ошибку. В пространстве Y наблюдения не точка (элемент пространства), а область пространства
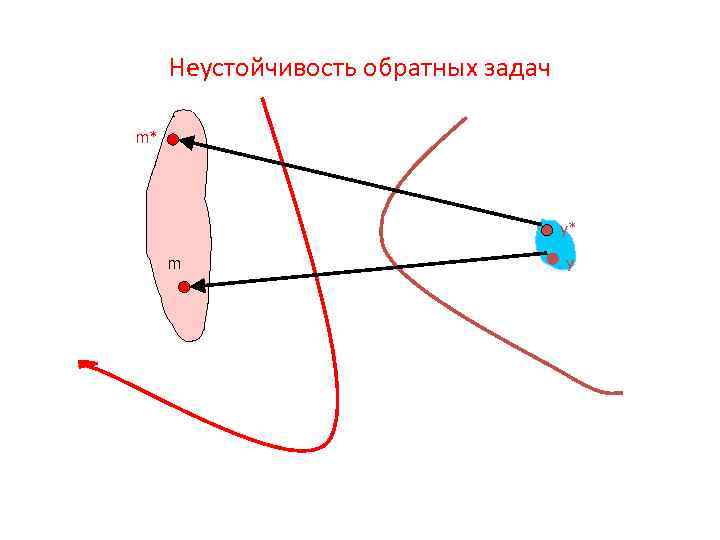
Неустойчивость обратных задач m* y* m y
Неустойчивость обратных задач • Даже если обратная задача будет иметь единственное решение из-за ошибки наблюдений области в пространстве Y будет соответствовать область в пространстве моделей • Неустойчивость оператора обратной задачи, что область решения может включать самые разные модели, в том числе очень далекие от истинной. ДЛЯ ПРЕОДОЛЕНИЯ НЕУСТОЙЧИВОСТИ НЕОБХОДИМО ВВЕДЕНИЕ АПРИОРНЫХ ОГРАНИЧЕНИЙ НА РЕШЕНИЕ
Основные проблемы решения обратных задач • Параметризация модели- выбор пространства M • Сопоставление экспериментальных и модельных значений поля -выбор критерия близости точек в пространстве Y • Определение критерия выбора единственного решения из множества решений • Сужение области решения, в случае неустойчивости задачи • Оценка качества решения – насколько полученное решение соответствует реальной модели
Линеаризация оператора прямой задачи
Линеаризация оператора прямой задачи • Только в задачах магнитометрии и гравиметрии имеет место линейность оператора прямой задачи. • Если среда разбита на блоки с постоянными значениями плотности в каждом из них • В случае задачи о контактной поверхности – определяется положение границы Z(x), разделяющей слои с разной плотностью , оператор решения прямой задачи не будет линейным
Линеаризация оператора прямой задачи • Таким образом, в большинстве случае оператор решения обратной задачи не является линейным • С другой стороны, большинство методов решения обратных задач разработано для линейных задач. • Выход – ЛИНЕАРИЗАЦИЯ ОПЕРАТОРА ПРЯМОЙ ЗАДАЧИ
Линеаризация оператора прямой задачи • В классическом случае обратная задача формулируется как поиск неизвестных параметров m по заданному оператору F( в общем случае нелинейному) и наблюденному геофизическому полю
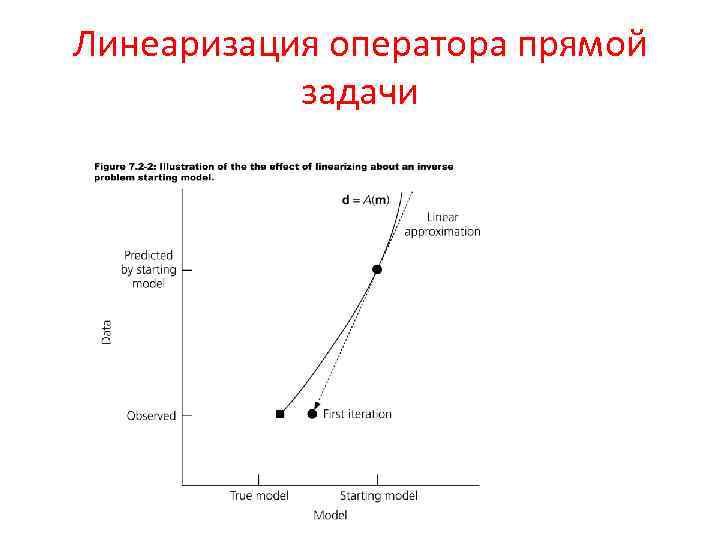
Линеаризация оператора прямой задачи • В случае линеаризации обратная задача формулируется как поиск поправок Δm к некоторому начальному приближению m(0) • В этом случае связь между Δm и Δy приблизительно будет линейной • Чем ближе начальная модель к истинному решению, тем лучше будет результат • В процессе линеаризации на каждом шаге решается линейная задача. Процесс сходится, когда поправка Δm станет достаточно малой
Линеаризация оператора прямой задачи: годограф отраженной волны • Оператор решения прямой задачи • Модель m: (m 1, m 2, m 3) определяется тремя параметрами: 1. H – глубина залегания отражающей границы 2. v – скорость в верхнем слое 3. φ – угол наклона отражающей границы
Линеаризация оператора прямой задачи: годограф отраженной волны • Шаг 1 – задаем начальный вектор m 0(h 0, v 0, φ0) • Шаг 2 – рассчитываем вектор t 0(x) – годограф для модели с начальными параметрами • Шаг 3 – рассчитываем Δt(x)=t(x)- t 0(x) • Шаг 4 – решаем линейную систему уравнений относительно Δm 1 : (Δh, Δv, Δ, φ) • Шаг 5 –корректируем начальную модель и получаем модель m 1= m 0+ Δm 1 Повторяем шаги 2 -5 пока Δmn не станет достаточно малым
Линеаризация оператора прямой задачи
Скачать презентацию Некорректность обратных задач Множество решений Геофизические наблюдения
Некорректность ОЗ_3.ppt